はじめに:広告は本当に効いたのか?
あるECサイトで新しい広告キャンペーンを実施しました。
広告を見たユーザー: 1000人中300人が購入(購入率30%)
広告を見なかったユーザー: 1000人中200人が購入(購入率20%)
差は10ポイントです。「広告のおかげで購入率が10%上がった!」と報告したくなりますが、これは正しいのでしょうか。
実は、広告を見たユーザーは単にもともと買いやすい層だったかもしれません。
本当に知りたいのは、もし広告を見せていなかったら、このユーザーたちは何人購入していたかです。
この「もしも」を統計的に扱うのが因果推論(Causal Inference)です。
「見えない世界」を想像する
潜在的アウトカムという考え方
因果推論の出発点は潜在的アウトカム(Potential Outcome)という発想です。各ユーザーには、2つの潜在する結果があるとする考え方です。
実際に観測できるデータで考えてみましょう。広告効果の事例の場合、実際に観測された結果 $Y$は以下のように考えることができます。
- $Y(1)$: 広告を見た場合の購入結果
- $Y(0)$: 広告を見なかった場合の購入結果
それぞれの場合において、購入結果$Y(1)$、$Y(0)$は(1=購入、0=非購入)のどちらかの値をとります。
$Y(1), Y(0)$は「もし〜だったら」という想像上の潜在的結果です。この結果は処置$T$のどちらを経験したかで決まります。
- $T$:処置(広告を見た=1、見ていない=0)
$Y(T)$の引数はこの処置を表しています。
これらの定義をもとに、実際に観測結果は以下のように考えることができます。
$$Y = T \cdot Y(1) + (1-T) \cdot Y(0)$$
この式は、「どちらの世界のYが観測されたかは、Tの値で決まる」という一致性(consistency)仮定を表しています。
因果効果とは
個人レベルでは、次のように定義できます。
$$\tau_i = Y_i(1) - Y_i(0)$$
これは「あるユーザー$i$にとって広告を見た場合と見てない場合で購入確率がどれだけ変わるか」という量です。
ところが、現実では、どちらか一方しか観測できません。この「もう一方の見えない世界」を反事実(Counterfactual)と呼びます。
| ユーザー | 観測結果 | 反事実 |
|---|---|---|
| A | 広告を見た → 購入(Y(1)=1) | 見なかったら? (Y(0)=?) |
| B | 広告を見た → 購入せず(Y(1)=0) | 見なかったら? (Y(0)=?) |
| C | 広告を見なかった → 購入せず(Y(0)=0) | 見ていたら? (Y(1)=?) |
$Y_i(1)$と$Y_i(0)$を同時に観測できないため、個人レベルの因果効果は直接観測できません。これを因果推論の根本問題といいます。
平均処置効果(ATE)
個人ではわからなくても、集団平均なら推定可能です。
$$
\text{ATE} = E[Y(1) - Y(0)] = E[Y(1)] - E[Y(0)]
$$
これは「全員に広告を見せた場合」と「全員に見せなかった場合」で、平均的にどれだけ購入率が変わるか?を表しています。このATEを推定することが因果推論の基本目標の一つとなります。
補足
「処置の効果があったか」という処置群平均効果(ATT : Average Treatment effect on the Treated) が関心になる場面も多いので、ATTが推定の目標になる場合があります。広告の事例では「広告を見た人に対する平均効果」となります。
$$ATT = E[Y(1)-Y(0)\mid T=1]$$
単純な平均差比較の問題
平均的な広告効果(集団平均効果)を知りたい場合、「広告を見た人の平均購入率」と「見なかった人の平均購入率」を単純に比較してしまいがちです。数式で書くと次のようになります。
$$
E[Y(1)|T=1] - E[Y(0)|T=0]
$$
これは広告の真の因果効果ではありません。
なぜなら、$E[Y|T=1]$は「広告を見た人の世界の平均」であり、$E[Y(1)]$ が表す「全員に広告を見せた場合の平均」とは異なります。($E[Y|T=0]$も同様です。)
これはT=1とT=0の異なる群間の購入率を比較した、単なる群間平均差を表しているにすぎません。
数式による検証
単純な平均差についてもう少し検証してみます。観測された差は次のように分解できます。
\begin{align}
E[Y|T=1] - E[Y|T=0]
&= \underbrace{E[Y(1)|T=1] - E[Y(0)|T=1]}_{\text{処置群(T=1)への因果効果(=ATT)}} \\
&\quad + \underbrace{E[Y(0)|T=1] - E[Y(0)|T=0]}_{\text{選択バイアス}} \\
\end{align}
第1項は「広告を見た人(処置群)が、もし広告を見なかったらどうだったか」との差で、処置群に対する因果効果(ATT)です。$Y(1)|T=1$が観測結果で、$Y(0)|T=1$が反事実となります。
第2項は「もし広告を見なかった場合における、処置群(T=1)と対照群(T=0)の平均結果の差」を表します。これは広告に関係のない、もともとの購買傾向の違いを表しており選択バイアスと呼ばれます。
直観的な理解
広告をクリックした人は、もともとブランドに関心が高い
→ 広告なしでも買いやすい
→ 「広告を見た人がもし広告を見なかった場合の購入率」 > 「広告を見なかった人の購入率」
→ $E[Y(0)|T=1] > E[Y(0)|T=0]$
となり、単純な平均差(ナイーブな比較)では、因果効果を過大/過少評価しがちになります。
相関と因果推論の比較
ナイーブな比較
では、ここからは実験データをもとに、単純な平均差でどう誤るのかを体感してみましょう。
以下は購入確率を生成するスクリプトです。広告による購買促進の効果が約4~5%程度に調整されたデータを生成します。
import pandas as pd
import numpy as np
rng = np.random.default_rng(42)
n = 2000
df = pd.DataFrame({
'user_id': np.arange(1, n+1),
'past_purchases': rng.poisson(3, n) # 過去の購買回数
})
# 各ユーザーが確率 p_T(ロジスティックで定義された値)に従って、
# 広告を見たか(T=0 or 1)を設定
# - past_purchasesが大きいほど広告を見やすい
# - どんなpast_purchasesのユーザーも広告を見る確率は一定ある
logits_T = -0.5 + 0.3 * df['past_purchases']
p_T = 1 / (1 + np.exp(-logits_T))
df['ad_exposure'] = rng.binomial(1, p_T)
# 真のデータ生成(ロジット差=係数betaTが真の因果効果)
beta0, betaX, betaT = -1.5, 0.35, 0.20
logits_Y = beta0 + betaX * df['past_purchases'] + betaT * df['ad_exposure']
p_Y = 1 / (1 + np.exp(-logits_Y))
df['purchase'] = rng.binomial(1, p_Y)
# 広告をみた人の平均購入率
ad = df.loc[df['ad_exposure']==1, 'purchase'].mean()
# 広告を見なかった人の平均購入率
no_ad = df.loc[df['ad_exposure']==0, 'purchase'].mean()
print(f"広告を見た人: {ad:.1%}")
print(f"広告を見ていない人: {no_ad:.1%}")
print(f"観測差: {ad - no_ad:.1%}")
# 真のATE(ロジット差から確率差を算出)
sigmoid = lambda z: 1/(1+np.exp(-z))
p1 = sigmoid(beta0 + betaX * df['past_purchases'] + betaT)
p0 = sigmoid(beta0 + betaX * df['past_purchases'] + 0)
true_ATE = (p1 - p0).mean()
print(f"{true_ATE:.1%}")
結果
広告を見た人: 43.6%
広告を見ていない人: 33.1%
観測差: 10.5%
真のATE: 4.5%
単純な平均差では約10.5ポイントとなり、真の広告効果から約6ポイント過大評価されていることがわかります。選択バイアス(過去購入回数が多いほど広告を見やすい)の影響を受けたためです。
選択バイアスを取り除く
このようなバイアスが生じるのは、処置(広告の表示)と観測結果(購買)の両方に影響を与える第三の要因が存在するためです。そのような要因があると単純に「広告→購買」という因果関係としては解釈できません。
この問題を解くために、データの背後にある因果構造をモデル化し、各変数間の関係を整理する必要があります。
DAG(因果グラフ)
検証用に生成したデータでは、過去の購買回数をユーザー毎に割り振り、購入回数が多いほど広告が多く表示されるように調整していました。この因果関係を図にしてみます。
過去の購買回数 (X)
↓ ↓
広告 (T) → 購入 (Y)
この図は「過去購買回数(X)」が「広告を見るか(T)」にも「購入するかどうか(Y)」にも影響していることを表しています。
このように、処置と結果の両方に影響する変数が存在すると、交絡(confounding)が生じます。この交絡を引き起こす変数$X$のことを、共変量(covariate)または交絡因子と呼びます。
ここで $X$(過去の購買回数)に条件づけるとは、購買傾向が同じような人、つまり同一ユーザーだったとしたらという条件のもとで広告を見る場合と見ない場合を比較することを意味します。
この操作によって、購買意欲の違いによるバイアスを取り除くことができるようになり、$T$ → $Y$ (広告 → 購買)の真の因果効果を識別できるようになります。
このように、交絡を引き起こす変数の影響をコントロールすることを、因果推論の理論ではバックドア基準を満たすというように呼びます。
なお、交絡を直接観測できない場合でも、X→T→M→Yという媒介変数Mを利用して因果効果を識別するフロントドア基準という手法もありますが、ここでは割愛します。
広告の例では、属性Xを観測できず、XがTとYの両方に影響(交絡)しているためにT→Yの因果効果を直接推定できないユーザー群に対して、「属性X → 広告T → 購買ページ閲覧M → 購買Y」という経路のうち、「購買ページ閲覧」という媒介変数Mだけが観測できる場合に対応します。
このとき、Mを介した経路の構造が正しく、かつMがT以外の要因から影響を受けないという強い仮定が成り立てば、交絡Xを観測せずともT→Yの因果効果を識別できることがあります。
因果効果の識別のための仮定
実際にこのような調整を行って因果効果を正しく識別するためには、次の3つの仮定が必要となります。これらはデータから因果関係を引き出すための理想条件です。
無交絡性(Ignorability)
$${Y(1), Y(0)} ⟂ T \mid X$$
観測した共変量 $X$(ここでは購買履歴など)で条件づければ、処置$T$の割当はランダムとみなせるという仮定です。
「購買意欲」などの違いをXで説明できていれば、同じXの中では「広告を見るかどうか」と「もともと潜在的に持っている購買傾向」は確率的に独立である、という想定です。
重なり性(Positivity/Overlap)
$$0 < P(T=1|X) < 1$$
どんなタイプの人でも、少なくとも一部は広告を見ており、また一部は見ていない、という仮定です。
もし「常に広告を見る人」や「絶対に見ない人」がいたら、その人については比較対象(反事実)を観測できないため因果効果を推定できません。この条件は、効果検証できる可能性が対象者全員に存在していることを要請しています。
SUTVA(Stable Unit Treatment Value Assumption)と一致性
他人の処置は自分に影響せず(非干渉)、処置の定義は一意で、観測結果は $Y = Y(T)$ を満たす、という仮定です。ある処置を受ける人それぞれにおいて、その処置の効果が安定しているという要請です。
補足:現実データでの破れ
ここで紹介した「無交絡性」「重なり性」「SUTVA(非干渉・一致性)」は因果効果の識別に必要な仮定ですが、実際のデータではそれらの条件を破るケースがあります。以下で、代表的なケースと対処法をまとめます。
無交絡性の破れ
仮定
- 観測できる変数$X$で交絡をすべて制御できる
破れやすい場面
- モチベーション・嗜好・健康意識など、データ化できない因子がある
- 外部要因(天候・トレンド)
対処法
- ログで測れない変数がありそうな場合、設計側で交絡を壊す仕組みを考える
- 感度分析で「どれだけの交絡があれば結果が変わるか」を検証
- 差分の差分 (DiD)、断点回帰 (RD)など無交絡性に依存しない識別を使う
重なり性の破れ
仮定
- すべての$X$で処置群と非処置群が存在する
破れやすい場面
- 高齢層・常連層には広告をほとんど配信していない
対処法:
- 比較できるXの範囲で限定して効果測定する
- 極端なサンプルをクリッピング
- 局所的ATE(LATE)や共通領域限定の推定に切り替える
非干渉の破れ
仮定
- 他人の処置(広告表示など)が自分の結果に影響しない
破れやすい場面
- SNS・口コミ経由で広告効果が他ユーザーに伝播
- 家族・同居人・同地域への波及
対処法
- 個別ユーザー単位の独立性が怪しいときは、干渉が少ない最小単位での分析を検討
- クラスタ単位で処置を割り当てる(地域・ユーザー群など)
- ネットワーク干渉モデルや spillover 推定を導入
処置の一貫性の破れ
仮定
- T=1 が常に同じ介入を意味する
破れやすい場面
- 広告がバナー・動画・SNS投稿など複数種を含む
- 同じ広告でも表示面・タイミングが異なる
対処法 - 「T=1 が何を意味するか」を明確化する
- メディア別・チャネル別に分析
- 処置効果の異質性(CATE)を可視化
サンプル独立性の破れ
仮定
- 各サンプルが独立同分布である
破れやすい場面
- 同一キャンペーン内でのユーザー依存(クラスタ相関)
- 時系列構造(季節性、トレンド)
対処法
- ユーザー・時間・地域などの依存構造を意識したモデルを利用、または標準誤差で調整
- 階層ベイズ・マルチレベルモデルで構造を明示的にモデリング
- クラスタロバスト標準誤差(clustered SE)を使用
- 時系列構造では差分の差分 (DiD) や季節調整を導入
交絡を取り除く考え方
理想的には、「過去購買回数 X が同じ人同士」で比較すれば、交絡の影響を消して純粋な因果効果を推定できます。数式で書くと以下のようになります。
\begin{align}
E[Y(1)] = E_X[E[Y\mid T=1, X]] \\
E[Y(0)] = E_X[E[Y\mid T=0, X]]
\end{align}
つまり、Xで条件づけて(層別化して)平均を取ることができれば交絡は消えるというのが因果推論の基本原理です。(反復期待値の法則)
補足
上の識別式を正当化するのに十分なのは、無交絡性より弱い平均交換可能性(Mean Exchangeability) です。具体的には
$$
E\big[Y(t)\mid X, T\big] = E\big[Y(t)\mid X\big]\quad (t\in{0,1})
$$
が成り立てば、
$$
E[Y(t)] = E_X\big[E[Y\mid T=t, X]\big]
$$
が導かれます。直感的には、「同じ (X) の人たちの平均的な潜在結果は、処置群/対照群で同じ」と仮定しているだけであり、分布全体の独立(完全な無交絡性)よりも弱い要請です。
なお、無交絡性 ⇒ 平均交換可能性 ⇒ 上式(反復期待値による識別) の順で、要請は弱くなります。
傾向スコア
これまで説明してきたように、交絡を取り除くためには「$X$ごとに層別化」して比較する必要があります。
しかし、実際には$X$が多次元(年齢、地域、購買履歴、端末など)だと、「Xごとに層別化」するのは現実的でありません。
この問題を解決するために、次の重要な性質を利用します。
すべての$X$を条件にする代わりに、$e(X)$という1つの要約値(バランシングスコア)で条件づけても、$$T \perp X \mid e(X)$$ が成り立つ。
ここで登場する$e(X)$は傾向スコア(Propensity Score)と呼ばれるものです。これは「各ユーザーが広告を見る確率」を、共変量 $X$ から推定したもので次のように定義されます。
$$
e(X) = P(T=1|X)
$$
傾向スコアは「観測された共変量$X$の情報を1つの確率値にまとめたもの」であり、広告の文脈では「ユーザーが広告を見る確率」を意味します。
共変量X(過去の購買回数、年齢、性別など)の情報から、その人が処置(T=1)を受ける確率を推定します。一番基本的なのがロジスティック回帰ですが、2値分類モデルであれば代用できます。
傾向スコアによる補正(IPW)
傾向スコア $e(X)$ を利用すると、処置群と非処置群の偏りを重み付けによって補正できます。この方法を 逆確率重み付け(Inverse Probability Weighting: IPW) と呼びます。
IPWによる平均処置効果(ATE)の推定式は次の通りです。
$$
\widehat{ATE}_{\text{IPW}} = \frac{1}{n}\sum_i\left(\frac{T_iY_i}{e(X_i)} - \frac{(1-T_i)Y_i}{1-e(X_i)}\right)
$$
IPWの考え方は、確率的に珍しいケースを重く扱うことです。
- 広告を見る確率が低いのに実際に見た人 → 重く扱う(貴重なケース)
- 広告を見やすい人 → 軽く扱う(よくあるケース)
このように重み付けを行うことで、両群の共変量分布を一致させ、まるでランダム割付のような状態(バランスの取れた擬似母集団)を再現します。
実装例
以下は、ロジスティック回帰による傾向スコア推定と、IPW推定の実装例です。
このコードでは、以下のようにATEを推定しています
- ロジスティック回帰で傾向スコアを推定
- 極端値をクリッピングして安定化
- IPWによって処置群・非処置群のバランスを取る
最後に 標準化差分(Standardized Mean Difference: SMD) によって、重み付け前後のバランス改善を確認します。
import numpy as np
import pandas as pd
from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
# 1) 傾向スコアの推定(ロジスティック、単変量例)
sc = StandardScaler()
X = sc.fit_transform(df[['past_purchases']].values)
T = df['ad_exposure'].values
Y = df['purchase'].values
ps = LogisticRegression(max_iter=2000)
ps.fit(X, T)
e = ps.predict_proba(X)[:, 1]
# 2) クリッピング(極端重み対策)
e = np.clip(e, 0.05, 0.95)
df['propensity'] = e
# 3) IPW推定:2通りのどちらかに統一して使う
## 3-1) Horvitz–Thompson型
ate_ipw_ht = (T*Y/e - (1-T)*Y/(1-e)).mean()
## 3-2) Hajek型
w_t = T / e
w_c = (1 - T) / (1 - e)
mu1 = (w_t * Y).sum() / w_t.sum()
mu0 = (w_c * Y).sum() / w_c.sum()
ate_ipw_hajek = mu1 - mu0
print(f"IPW (HT型) ATE: {ate_ipw_ht:.4f}")
print(f"IPW (Hájek) ATE: {ate_ipw_hajek:.4f}")
# 4) バランス診断:SMD(重み付け無し / 重み付け有り)
def smd_unweighted(x, t):
m1, v1 = x[t==1].mean(), x[t==1].var(ddof=1)
m0, v0 = x[t==0].mean(), x[t==0].var(ddof=1)
return (m1 - m0) / np.sqrt(0.5*(v1 + v0))
def wmean(x, w):
return (w*x).sum()/w.sum()
def wvar(x, w):
m = wmean(x, w)
return (w*((x - m)**2)).sum()/w.sum()
def smd_weighted(x, t, w_t, w_c):
# treated
x1, ww1 = x[t==1], w_t[t==1]
x0, ww0 = x[t==0], w_c[t==0]
m1, v1 = wmean(x1, ww1), wvar(x1, ww1)
m0, v0 = wmean(x0, ww0), wvar(x0, ww0)
return (m1 - m0) / np.sqrt(0.5*(v1 + v0))
x = df['past_purchases'].values
smd_before = smd_unweighted(x, T)
smd_after = smd_weighted(x, T, w_t, w_c)
print(f"SMD before={smd_before:.3f}, after={smd_after:.3f}")
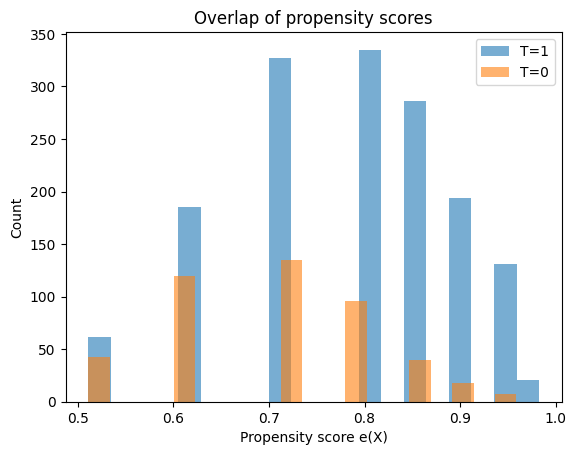
# 5) オーバーラップ確認(e(X) の分布)
plt.figure()
plt.hist(e[T==1], bins=20, alpha=0.6, label='T=1')
plt.hist(e[T==0], bins=20, alpha=0.6, label='T=0')
plt.xlabel('Propensity score e(X)')
plt.ylabel('Count')
plt.title('Overlap of propensity scores')
plt.legend()
plt.show()
結果
IPW (HT型) ATE: 0.0285
IPW (Hajek型) ATE: 0.0284
SMD before=0.536, after=-0.011
購買傾向そのもの(過去購買回数)を考慮して重み付けを行うと、効果は約+3%に低下しました。これは「広告を見やすい人はもともと購買意欲が高い」という交絡を補正した結果です。
IPWによる推定値(約+2.8〜3.0%)は、真の因果効果(+4.5%)に近く、SMDの改善(0.54→0.01)からもバランスが取れていることがわかります。
注意点
IPW推定は重みの安定性に依存するため、分析の前に傾向スコアの分布を確認する必要があります。今回のデータは両群のデータが重なっていることがヒストグラムから確認できますが、重なり性が破れている場合($e(X)$が0や1に近いサンプルが多い場合)は、推定は不安定になります。
他の推定手法
IPWのほかにも、交絡を補正して因果効果を推定するための方法があります。ここでは、マッチング(Matching)と回帰調整(Regression Adjustment)について、それぞれの直感と実装例を以下に示します。
マッチング(Matching)
類似した$X$(ここでは購買回数)をもつユーザーをペアにして比較します。
たとえば、「購買傾向が似ている2人」を見つけて、片方が広告を見た場合・もう片方が見なかった場合の購買率の差を比べます。
こうして「似た者同士」を比較することで、Xの影響をそろえた上での効果を求められます。
この方法では「処置群を基準にマッチング」を行うため、推定されるのは ATT(=処置群に対する平均効果 になります。
実装例(カーネルマッチング)
このコードでは、傾向スコアが近い対照群を複数人選び、距離に応じたカーネル重みを付けて比較することで、処置群に対する平均的な処置効果(ATT)を推定しています。
idx_t = np.where(T == 1)[0] # 処置群
idx_c = np.where(T == 0)[0] # 対照群
def epanechnikov_kernel(u):
"""Epanechnikov kernel: K(u) = 0.75(1-u²) for |u|≤1"""
# 距離が近いほど重みを大きく、遠いほど重みを小さくする
return np.where(np.abs(u) <= 1, 0.75 * (1 - u**2), 0)
# 評価するバンド幅(スムージングの強さ)候補
bandwidths = [0.01, 0.02, 0.05, 0.1]
for h in bandwidths:
att_kernel_list = [] # 個体別の推定効果(Y1 - Y0)
n_with_support = 0 # 共通サポート内(重みが正)の処置個体数
# 各処置個体 t について、対照群からの反実仮想アウトカムを推定
for t_idx in idx_t:
e_t = e[t_idx]
# 全対照者との距離を計算
u = (e[idx_c] - e_t) / h
weights = epanechnikov_kernel(u)
# 処置個体 t の近くに(傾向スコア的に)似た対照個体が存在
if weights.sum() > 0:
# 重みを確率に正規化
weights_norm = weights / weights.sum()
# 対照群アウトカムの加重平均(反実仮想 Y0 の推定)
y0_hat = (weights_norm * Y[idx_c]).sum()
# 個体別効果(観測Y1 - 反実仮想Y0)
att_kernel_list.append(Y[t_idx] - y0_hat)
n_with_support += 1
# 個体別効果の平均を ATT として出力
if len(att_kernel_list) > 0:
att_kernel = np.mean(att_kernel_list)
print(f"h={h:.2f}: ATT={att_kernel:.4f}, "
f"サポート内={n_with_support}/{len(idx_t)}")
else:
print(f"h={h:.2f}: サポートが不足")
h=0.01: ATT=0.0063, サポート内=1520/1541
h=0.02: ATT=0.0092, サポート内=1537/1541
h=0.05: ATT=0.0084, サポート内=1541/1541
h=0.10: ATT=0.0276, サポート内=1541/1541
回帰調整(Regression Adjustment)
処置 T と交絡因子 X を説明変数として、結果 Y をモデル化します。
回帰モデルの T の係数が、他の要因(ここでは X)を調整した上での因果効果を表します。
モデルの形式は次のようになります。
この例では、広告閲覧(ad_exposure)と過去購買回数(past_purchases)を説明変数として購買確率を推定し、広告のロジットスケール上での効果を算出しています。
実装例
from sklearn.linear_model import LogisticRegression
# ロジスティック回帰で「購買(purchase)」を目的変数
# ad_exposure、past_purchases)を説明変数として推定
logit = LogisticRegression(max_iter=1000)
logit.fit(df[['ad_exposure', 'past_purchases']], df['purchase'])
# 学習された回帰係数の取得
coef_T = logit.coef_[0][0] # 広告接触(処置変数 T)の係数
coef_X = logit.coef_[0][1] # 交絡要因(過去購買回数 X)の係数
intercept = logit.intercept_[0] # 切片項
# シグモイド関数(ロジット→確率変換)
sigmoid = lambda z: 1 / (1 + np.exp(-z))
# 処置群(広告を見た人)について
#「広告を見た場合(T=1)」と「見なかった場合(T=0)」の
# 購買確率をそれぞれ推定
# 実際に広告を見た人のデータのみ使用
treated_data = df[df['ad_exposure'] == 1]
# T=1(実際に広告を見た場合)の購買確率
p1_treated = sigmoid(intercept + coef_X * treated_data['past_purchases'] + coef_T * 1)
# T=0(反実仮想:もし広告を見なかった場合)の購買確率
p0_treated = sigmoid(intercept + coef_X * treated_data['past_purchases'] + coef_T * 0)
# ATT = 処置群における「T=1 と T=0 の確率差」の平均
ATT_from_logit = (p1_treated - p0_treated).mean()
print(f"\nATT: {ATT_from_logit:.1%}")
ATT: 2.6%
Doubly Robust(二重頑健)推定
ここまで紹介した IPW(重み付け)と回帰調整(アウトカムモデリング)は、いずれも交絡を補正して因果効果を推定する有力な手法です。ただし、どちらの方法もそれぞれに弱点があります。
- IPW:傾向スコア e(X) の推定モデルが誤るとバイアスが生じる
- 回帰調整:アウトカムモデルの指定を誤ると正しい推定にならない
これらの弱点を補うために生まれたのが、Doubly Robust(二重に頑健)推定 です。
Doubly Robust推定では、傾向スコアモデル(IPWの部分)とアウトカムモデル(回帰の部分)の両方を組み合わせて補正します。
そのため、どちらか一方のモデルが正しければ、一致推定(consistent estimator)となる性質があります。この「どちらか片方が正しければよい」という点が「二重に頑健(doubly robust)」という名前の由来です。
\widehat{ATE}_{DR} =
\frac{1}{n}\sum_i \Big[
\frac{T_i\{Y_i - \hat{\mu}_1(X_i)\}}{e(X_i)} -
\frac{(1-T_i)\{Y_i - \hat{\mu}_0(X_i)\}}{1-e(X_i)} +
\hat{\mu}_1(X_i) - \hat{\mu}_0(X_i)
\Big]
第一項と第二項で残差(予測誤差)を重み付けて補正し、
最後の項で予測値の平均差を加えることで、バイアスを減らしています。
実装例
import numpy as np
from sklearn.model_selection import KFold
from sklearn.linear_model import LogisticRegression
X_cf = df[['past_purchases']].values
T = df['ad_exposure'].values
Y = df['purchase'].values
e = df['propensity'].values
# 簡易 cross-fitting: 2-fold でアウトカムモデルの外部予測を作る
kf = KFold(n_splits=2, shuffle=True, random_state=42)
mu1_hat = np.zeros(len(df))
mu0_hat = np.zeros(len(df))
for tr, te in kf.split(X_cf):
# treated model: Y ~ X on treated
m1 = LogisticRegression(max_iter=2000).fit(X_cf[tr][T[tr]==1], Y[tr][T[tr]==1])
# control model: Y ~ X on control
m0 = LogisticRegression(max_iter=2000).fit(X_cf[tr][T[tr]==0], Y[tr][T[tr]==0])
mu1_hat[te] = m1.predict_proba(X_cf[te])[:,1]
mu0_hat[te] = m0.predict_proba(X_cf[te])[:,1]
# DR推定量(ATE)
dr1 = T*(Y - mu1_hat)/e
dr0 = (1 - T)*(Y - mu0_hat)/(1 - e)
ate_dr = (dr1 - dr0 + mu1_hat - mu0_hat).mean()
print(f"Doubly Robust (cross-fitted) ATE: {ate_dr:.4f}")
Doubly Robust (cross-fitted) ATE: 0.0202
近年は ML を用いた DML(Double Machine Learning) も有力です。
不確実性を考える:ベイズ因果推定
これまでの方法では、因果効果(ATEやロジット差)を1つの点推定値として求めてきました。
しかし現実のデータには不確実性があり、モデルパラメータや効果の値も「1つの真値」ではなく確率的にばらつく量として捉えることが自然です。
これを実現するのがベイズ因果推定(Bayesian Causal Inference) です。
ベイズ的考え方
ベイズ推定では、「広告効果」そのものを確率変数 $θ$として扱い、観測データ$D$を通じてその不確実性を更新します。
$$
P(\theta \mid D) \propto P(D\mid \theta) P(\theta)
$$
ここで
- $P(θ)$:事前分布 =効果に対する事前の信念
- $P(D∣θ)$:尤度 =データが観測される確率
- $P(θ∣D)$:事後分布 =データを見た後の効果の分布
となります。
つまり、「広告効果がどのくらいありそうか?」を分布として表現できるのがベイズ的アプローチの最大の特徴です。
PyMCによる実装(ロジスティック回帰)
以下では、PyMCを用いて「購買確率をロジスティックモデルで表し、広告効果($β_T$)」を事後分布として推定します。
このモデルでは、
- 広告を見たことによる購買確率のロジット差(=真の因果効果パラメータ$β_T$)
- サンプリング結果:効果の不確実性を反映した分布
が得られます。
実装例
import pymc as pm
import arviz as az
import numpy as np
X = df['past_purchases'].to_numpy()
T = df['ad_exposure'].to_numpy()
Y = df['purchase'].to_numpy()
with pm.Model() as model:
beta0 = pm.Normal('beta0', 0, 2)
betaX = pm.Normal('betaX', 0, 2)
betaT = pm.Normal('betaT', 0, 2) # 因果効果の主要パラメータ(ロジット差)
logit_p = beta0 + betaX * X + betaT * T
p = pm.math.sigmoid(logit_p)
pm.Bernoulli('Y_obs', p=p, observed=Y)
trace = pm.sample(2000, tune=1000, random_seed=42, target_accept=0.9)
az.summary(trace, var_names=['beta0', 'betaX', 'betaT'])
結果
| index | mean | sd | hdi_3% | hdi_97% | mcse_mean | mcse_sd | ess_bulk | ess_tail | r_hat |
|---|---|---|---|---|---|---|---|---|---|
| beta0 | -1.384 | 0.118 | -1.594 | -1.153 | 0.003 | 0.002 | 1991.0 | 2030.0 | 1.0 |
| betaX | 0.31 | 0.029 | 0.257 | 0.366 | 0.001 | 0.001 | 2054.0 | 2018.0 | 1.0 |
| betaT | 0.114 | 0.116 | -0.094 | 0.345 | 0.002 | 0.002 | 2226.0 | 2140.0 | 1.0 |
betaT はロジットスケールの効果(対数オッズ比)のため、確率差(購買率の差)に変換します。
$$\Delta p(x)=\sigma(\hat\beta_0+\hat\beta_X x+\hat\beta_T)-\sigma(\hat\beta_0+\hat\beta_X x)$$
ここで$\sigma(z)=1/(1+e^{-z})$はロジスティック関数です。
代表的な $X$ を固定して「広告を見たときと見なかったときの購買確率の差」を数値的に求めることで、ベイズ的な因果効果の分布を理解できます。
import numpy as np
sigmoid = lambda z: 1/(1+np.exp(-z))
p0 = sigmoid(-1.384 + 0.31*3) # 例: 平均的な購買傾向ユーザー
p1 = sigmoid(-1.384 + 0.31*3 + 0.114)
print(p1 - p0)
2.7%
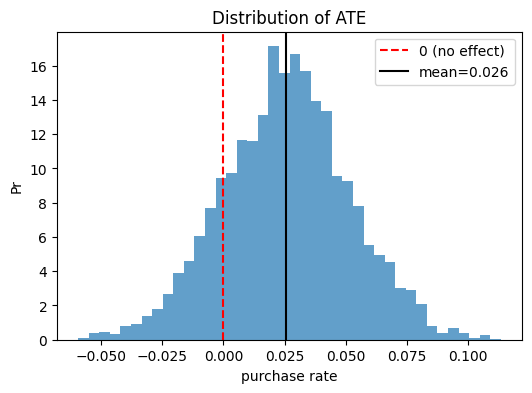
効果の可視化(事後分布)
下記は「広告効果がどの範囲にありそうか」を示す事後分布を表しています。
広告効果は、95%の確率でこの範囲にあると考えられる」というベイズ的な不確実性評価ができます。
import numpy as np
import matplotlib.pyplot as plt
import arviz as az
sigmoid = lambda z: 1/(1+np.exp(-z))
# 事後サンプルの抽出
beta0 = trace.posterior['beta0'].stack(draws=("chain","draw")).values
betaX = trace.posterior['betaX'].stack(draws=("chain","draw")).values
betaT = trace.posterior['betaT'].stack(draws=("chain","draw")).values
# 各サンプルについてATEを計算
Xv = df['past_purchases'].values
ate_samples = []
for b0, bx, bt in zip(beta0, betaX, betaT):
p1 = sigmoid(b0 + bx*Xv + bt)
p0 = sigmoid(b0 + bx*Xv)
ate_samples.append((p1 - p0).mean())
ate_samples = np.array(ate_samples)
# 結果の要約
mean_ate = ate_samples.mean()
ci_lower, ci_upper = np.percentile(ate_samples, [2.5, 97.5])
prob_positive = (ate_samples > 0).mean()
print(f"ATE posterior mean = {mean_ate:.3f}, 95% CI = ({ci_lower:.3f}, {ci_upper:.3f})")
print(f"P(ATE > 0) = {prob_positive:.1%}")
# 事後分布の可視化
plt.figure(figsize=(6,4))
plt.hist(ate_samples, bins=40, density=True, alpha=0.7)
plt.axvline(0, color='red', linestyle='--', label='0 (no effect)')
plt.axvline(mean_ate, color='black', linestyle='-', label=f'mean={mean_ate:.3f}')
plt.title('Distribution of ATE')
plt.xlabel('purchase rate')
plt.ylabel('Pr')
plt.legend()
plt.show()
ATE posterior mean = 0.026, 95% CI = (-0.026, 0.077)
P(ATE > 0) = 83.5%
ベイズ推定ではこのように、単なる点推定ではなく、効果の不確実性を分布として可視化できる点が大きな利点です。
推定の先にある世界
これまでの内容は平均的な広告効果を推定する手法でした。
ここから先では、推定をどう使いこなすかという考え方を整理します。
推定の使い分け
| 状況 | 推奨手法 | 理由 |
|---|---|---|
| データが豊富で交絡構造が明確 | IPW / DR | シンプルで高速、効果の解釈が容易 |
| データが少ない | ベイズ | 不確実性を分布として定量化できる |
| 階層的・非線形構造が複雑 | ベイズ | 階層モデルや非線形関係に柔軟に対応 |
| モデル誤指定に強い手法を求める | DR / DML | 二重頑健性によりロバストな推定が可能 |
個別因果効果(CATE)とUpliftモデリング
これまで扱ってきたのは、全体の平均効果(ATE)でした。しかし、「誰に効果があるか」が重要な場合があります。そのために考えるのが、条件付き平均処置効果(CATE)です。
\text{CATE}(x) = E[Y(1) - Y(0) \mid X = x]
これは、「購買傾向がこのくらいの人には広告がどれくらい効くか?」を推定します。
この個別効果の推定を活用した手法が Upliftモデリング です。
Meta-Learner(S/T/X-Learner) などの設計により、非線形な構造や特徴間の相互作用を柔軟に学習できます。
平均ではなく、人ごとに最適化された施策を考えるのがCATE・Upliftの目的です。
オフポリシー評価(Off-Policy Evaluation: OPE)
過去のログデータを使って、まだ実行していない新しい施策(ポリシー:広告の出し方ルール等)の効果を推定する場合も、基本的な考え方は同じです。
観測確率と新ポリシー確率の比である重要度重み(importance weight)を利用します。
w(x, a) = \frac{\pi_{\text{new}}(a \mid x)}{\pi_{\text{old}}(a \mid x)}
これにより、過去データに基づいて「新しいポリシーならどうなっていたか」を再現できます。
最も基本的な推定量は 逆確率重み付き推定量(IPS) です。
過去のログデータにおける各サンプルに重み $w_i$ をかけて平均を取ります。
\widehat{V}_{\text{IPS}} =
\frac{1}{n}\sum_{i=1}^n
w(x_i, a_i)\, y_i
これは「新ポリシーのもとで得られたであろう平均報酬(価値)」を推定する式です。
しかし、重みが極端に大きくなると分散が爆発するという欠点があるため以下の工夫が推奨されます。
- 自己正規化IPS(SNIPS):重みを合計でスケーリングして安定化
- DR-OPE(Doubly Robust OPE):重要度重み+アウトカムモデルの併用
- 重みのクリッピング:極端な値を制限して分散を抑制
まとめ
広告効果を因果で考えるという流れを通して、相関との違い、交絡の補正、そして不確実性の表現までを一通り見てきました。最後に、記事のポイントを整理します。
-
もし広告を見なかったら?を想像する
潜在的アウトカムで何と何を比べたいかを定義する -
平均差は因果ではない
観測平均差=因果効果+選択バイアス -
交絡を補正して因果を識別する
IPW・マッチング・回帰・DRを適切に活用 -
識別性の仮定とバランス診断
無交絡・重なり・SUTVAを意識し、重みの安定性を確認 -
不確実性を扱うベイズ的視点
効果を確率分布で理解し、意思決定に信頼度を添える