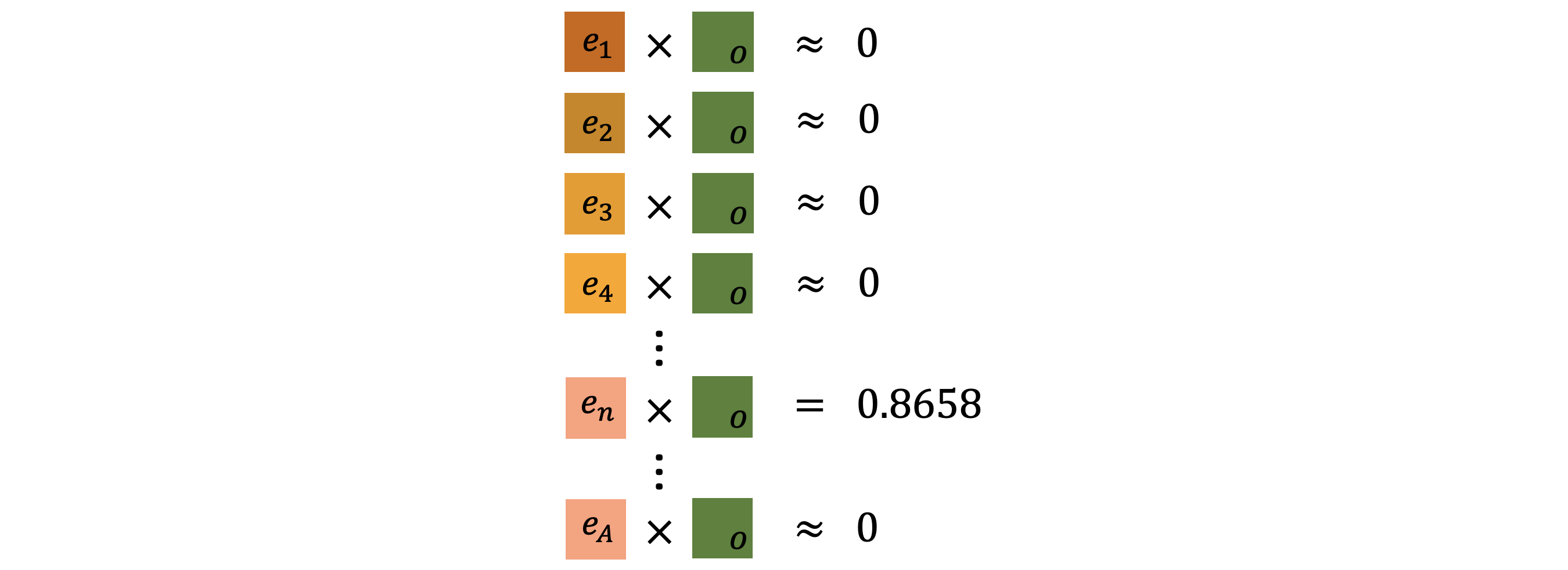この記事は
ChatGPTなどの大規模言語モデルの基盤技術となっているTransformerモデルを、なるべく数式を使わずにイラストで説明します。
最終セクションにある参考文献の内容をベースに、図・内容ともにかなり簡略化して説明しています。また、数学的な正確さ厳密性よりも、わかりやすさを優先しています。Transformerの全体を理解する一助になれば幸いです。
1. Transformerの全体図
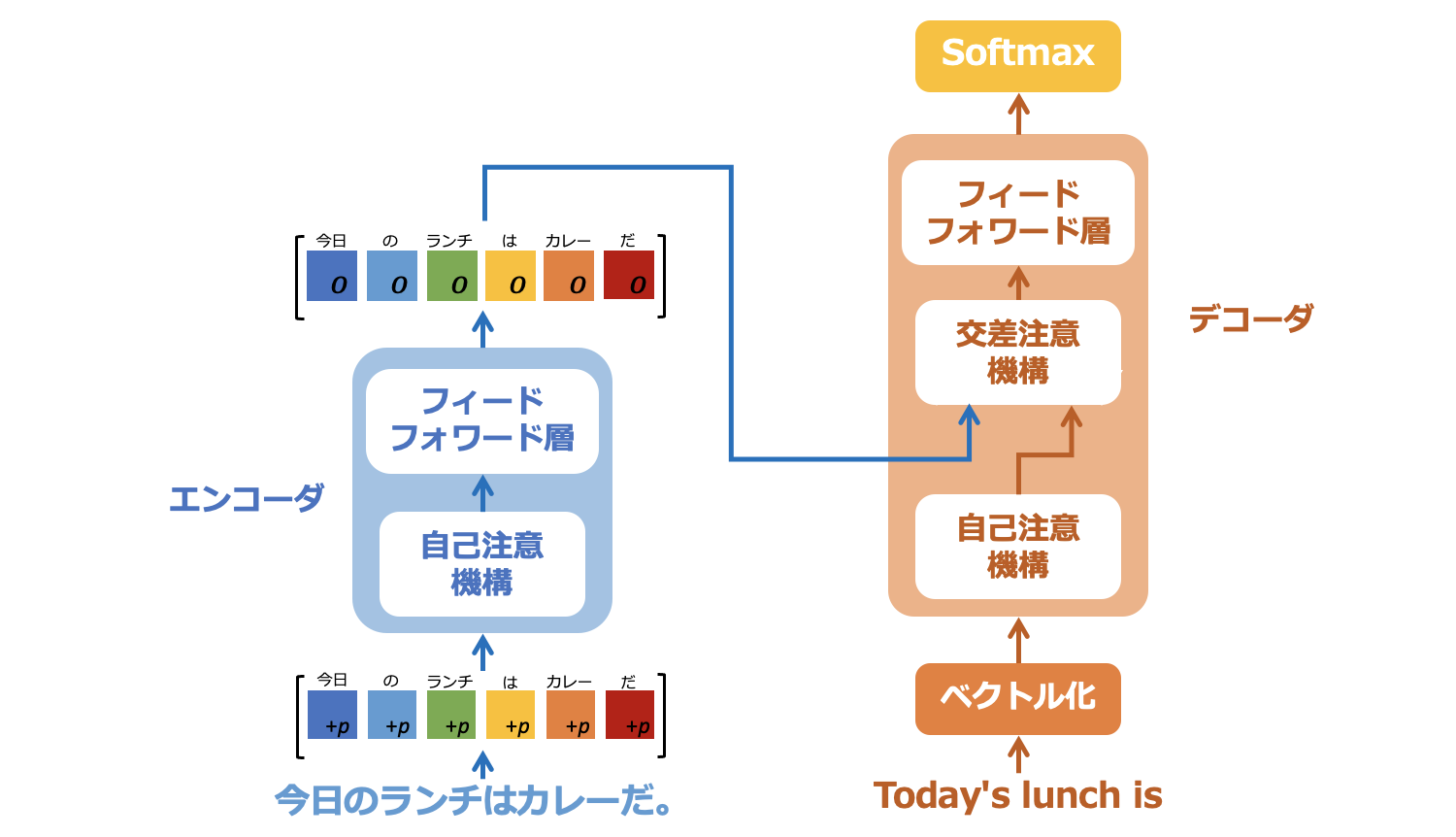
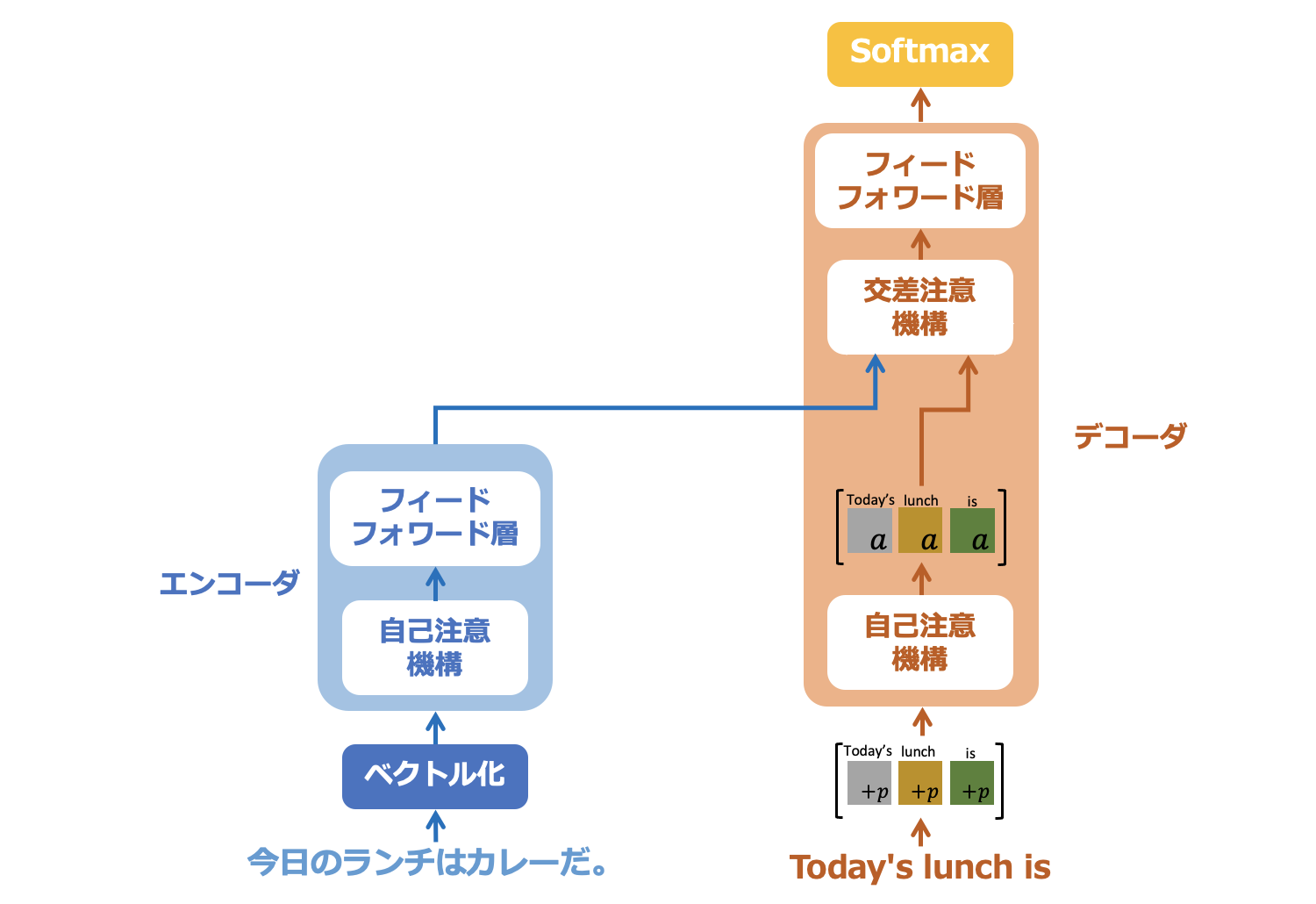
Transformerの全体図を図1-1に示しました。Transformerの提案論文 "Attention is all you need" で説明されている図はもう少し複雑な構造となっていますが、ここでは理解を優先するため、重要な部分を残してかなり簡略化しています。
Transformerは大きく、エンコーダとデコーダに分かれています。Transformer内部の処理は極めて複雑なため、実際にデータ流れを追って何が行われているのか人間が理解しようというのは不可能です。そのため、「おそらくこのようなことが行われている」という想像で説明しています。
図1-1: Transformerの全体図
1.1. エンコーダの概要
エンコーダでは、ベクトル化した入力データを自己注意機構へと入力します。エンコーダの自己注意機構では、入力されたベクトルに対して、そのベクトル内のどこに注目して処理を進めるべきかを学習します。
次に、自己注意機構からの出力ベクトルはフィードフォワード層へ入力されます。フィードフォワード層では、自己注意機構で特徴付けられたベクトルが、より表現力が豊かになるようにさらに学習されます。エンコーダからの出力は、入力と同じ次元のベクトルです。
1.2. デコーダの概要
デコーダでは、ベクトル化された入力データはエンコーダと同様に自己注意機構へ入力されます。デコーダの自己注意機構でも、入力されたベクトルに対して、そのベクトル内のどこに注目して処理を進めるべきかを学習します。なお、この記事では、エンコーダの自己注意機構とデコーダの自己注意機構は同じ構造のものとして扱っています。
デコーダの自己注意機構を経た入力ベクトルは、交差注意機構へ入力されます。この時に、エンコーダからの出力ベクトルも交差注意機構へと入力されています。交差注意機構では、デコーダの自己注意機構の出力ベクトルに対して、エンコーダからの出力ベクトルの必要な情報を追加するように学習が行われます。
こうして交差注意機構で必要な情報が「交差」したベクトルは、フィードフォワード層でさらに学習が行われ、デコーダから出力されます。デコーダからの出力ベクトルは、ソフトマックス関数で確率分布へと変換され最終的なTransformerの出力となり、ようやく人間にとって意味のあるデータへと変換されます。
以降のセクションでは、この図にあるTransformerの重要部分である、入力データのベクトル化、位置情報埋め込み、自己注意機構、交差注意機構を説明します。
2. Transformerの学習と推論
Transformerは提案されたとき、機械翻訳での活用を想定されたアルゴリズムでした。機械翻訳の入力データは文章です。なので、この記事での説明も機械翻訳を想定し、入力データを文章として説明します。
2.1. 学習時のデータの入出力
学習時は莫大な量の学習データを利用します。GPTの初代バージョンであるGPT-1では、約7,000冊の書籍がデータとして入力されたそうです。以下の文章について考えます。
図2−1:学習時に使う例文
このセクションでは、図2−1にあるように、そのような膨大なデータの一部として「明日のランチは何ですか？」と "What is tomorrow's lunch?" の訳の対を学習する場合を例にします。
図2-2: 学習時のエンコーダへの入力
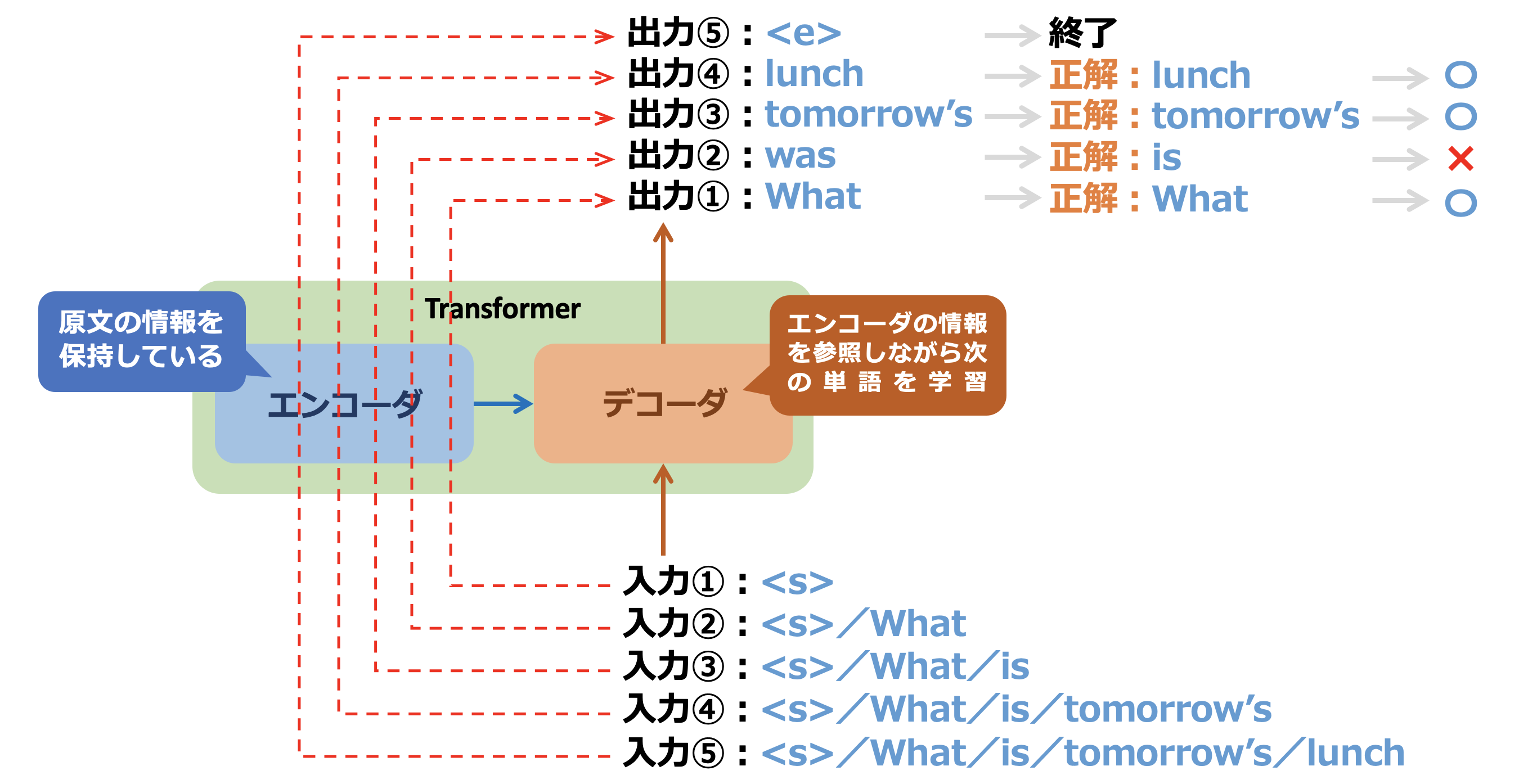
図2-2は、図1-1の簡易化されたTransformer全体図をさらに簡易化したものです。原文は「明日／の／ランチ／は／何／ですか」というように単語で分割されてエンコーダに入力されます。このとき、一度に全ての単語が入力されます。エンコーダは入力データを元に学習を行い、その結果、エンコーダは原文についての情報を保持している状態となります。
図2-3: 学習時のデコーダへの入力
図2-3は、エンコーダが原文の情報を学習した状態で、デコーダに翻訳文を入力しています。入力文を "What／is／tomorrow's／lunch" と単語に分割して入力するところはエンコーダと同じですが、分割した単語を一つずつ入力するところが異なります。
まず、図2-3の入力①では "<s>"という単語が入力されています。これは文章の先頭であることをTransformerに知らせる記号です。入力①はデコーダに入力され、エンコーダから原文の学習情報を参照し、デコーダ自身も学習しながら翻訳文の最初の単語を推測します。出力①では "What" という単語が推測されました。これは正解の "What" と同じ単語です。
次に、入力②では、正解の単語の組合せ "<s>／What" が入力されます。その結果、出力②は "was" となっています。これは正解の "is" とは違う単語です。
以降は、Transformerが予測した単語の正誤を記録しながら、文章の最後を示す記号 "<e>" が出力されるまで入力を繰り返します。その結果、最終的な出力は "What was tomorrow's lunch" という文となり、正解の訳文とは異なるものとなりました。これを正しい文章が出力されるまで、エンコーダ・デコーダを繰り返し訓練させるのが、Transformerでの学習フェーズです。
2.2. 推論時のデータの入出力
それでは、学習が完了したTransformerモデルで翻訳文を出力させてみます。例文として「今日のランチはカレーだ。」を英語に翻訳して出力させようと思います。以下の文章について考えます。
図2−1:推論時に使う例文
図2-2: 推論時のエンコーダへの入力
エンコーダへの入力は、図2−2のように、原文を「今日／の／ランチ／は／カレー／だ」のように単語に分割したものです。ここでも一度に全ての単語が入力されます。エンコーダは入力データを元に学習を行い、その結果、エンコーダは原文についての情報を保持している状態となります。
図2-3: 推論時のデコーダへの入力
続いて、図2−3ではデコーダから訳として推論された単語を1つずつ出力させます。デコーダへはそれまでに出力された単語の並びを1つずつ追加しながら入力し、それから推論される次の単語が出力されます。
入力①では、文章の先頭であることを示す記号"<s>"を入力します。デコーダは、この情報とエンコーダからの情報を参照しながら最初の単語を推測します。その結果、デコーダからの出力①として "Today's" が出力されました。
次に入力②では、入力①に出力①を追加した "<s>／Today's" を入力します。デコーダはこれに続く単語を推論し、出力②として ”lunch” を出力しました。
次に入力③では、入力②に出力②を追加した "<s>／Today's／lunch" を入力します。デコーダはこれに続く単語を推論し、出力②として ”is” を出力しました。これを繰り返し、文章の最後であることを示す記号 "<e>" が出力されれば全ての推論は完了です。このようにデコーダは、それまでに推論された単語の並びを元に、次の単語を予測することを繰り返して最終的な翻訳文を完成させます。
3. 入力データのベクトル化
Transformerの内部で利用されるデータは全てベクトルです。したがって、入力するデータもベクトルにして入力する必要があります。
3.1. トークンとは
トークンとは、Tranformerで扱うデータの単位です。入力される文章は、まずトークンに分割されます。ここまで文章は単語で分割されるとしてきましたが、実際はトークンに分割されます。分割するのはプログラマの作業ではなく、ライブラリの仕事です。どのように分割されるかはそのライブラリ次第ですが、たいていは名詞・動詞・助詞などの品詞で分割されるようです。ここから先はトークンで説明しますが、単語と読み替えてもだいたいOKです。
3.2. Transformerへのデータの入力
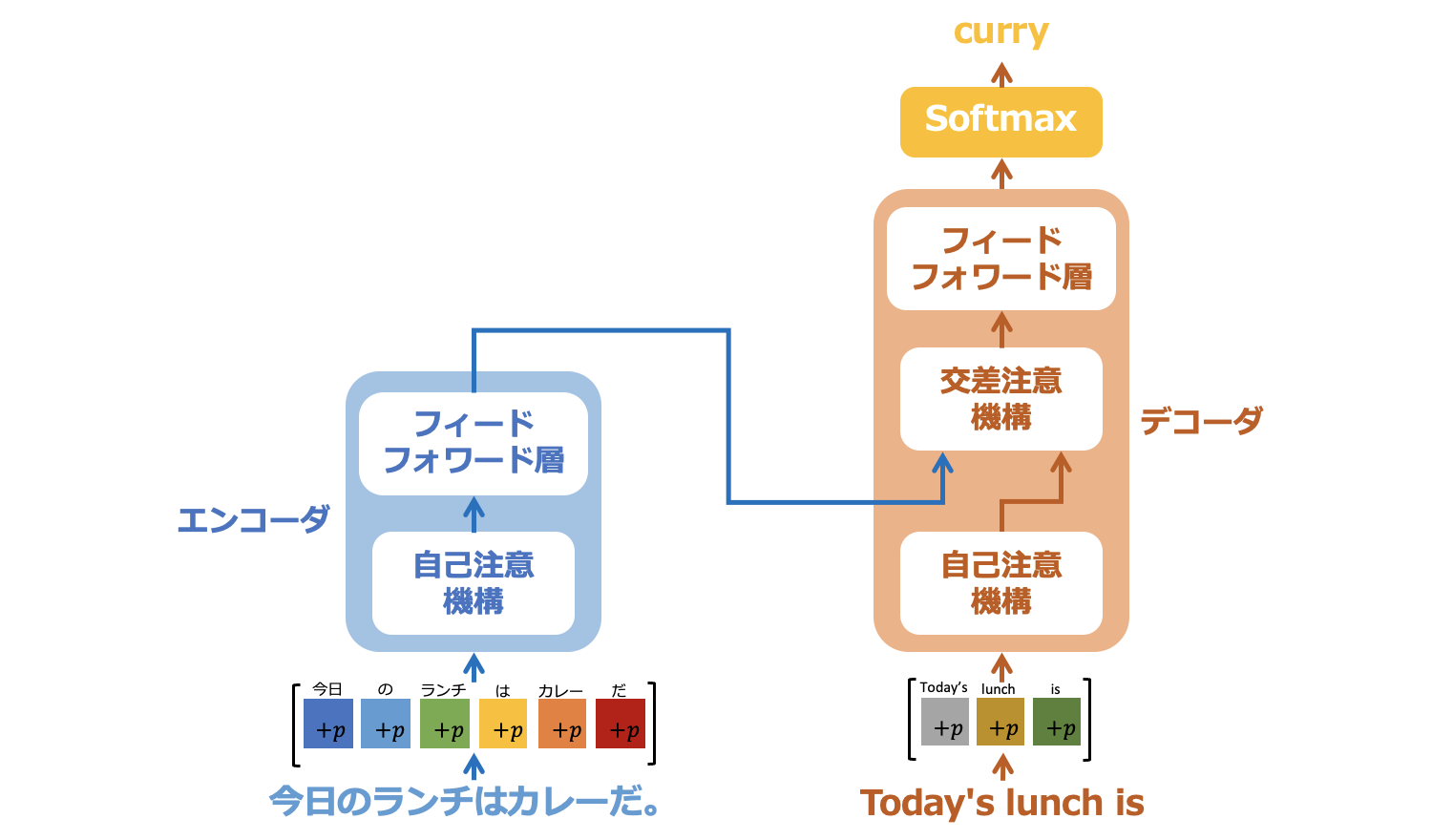
図3-1のように、データの入力はエンコーダとデコーダにそれぞれ行います。まず、エンコーダは原文である「今日のランチはカレーだ。」を受け取り、その結果をデコーダの交差注意機構へと出力します。一方、デコーダは原文の入力に対して、予測された英単語を一語ずつ出力することで翻訳を行います。プログラマは、デコーダが1単語ごとに推測した結果として、それまでに翻訳された文章を持っています。ここでは "Today's lunch is" まで翻訳が出力されているものとします。すると、デコーダにはこの文章に続く次の単語を予測して欲しいので、デコーダへの入力データは、これまで翻訳された文章 "Today's lunch is" となります。デコーダからは次の単語である "curry" が出力されます。
図3-1: Transformerのデータの入力先
3.3. 文章をトークンに分割
文章をベクトルへと変換する1つ目の手順です。まずは入力する文章をトークンへと分割します。ここでは分かりやすく、図3−2のように「今日／の／ランチ／は／カレー／だ／。」と分割されたものとします。
図3−2:トークンに分割された文章
すでに出力されている翻訳文である "Today's lunch is" も同様にトークン分割されます。
3.4. ベクトル化
次に分割された各トークンをベクトルに変換します。
3.4.1. ベクトルと埋め込み
Transformerを解説した技術書などを読んでいると、しばしば埋め込み(Embedding)という言葉が出てきます。埋め込みはベクトルと同じ意味と考えて良いようです。ベクトルに何か有用な情報が "埋め込まれて" いる状態のことを特に埋め込みと言うようです。"何か有用な情報" とは、例えば次で説明する位置情報などです。この記事ではどちらの場合もベクトルで統一します。
3.4.2. トークンのベクトル化
さて、変換されたベクトルは元のトークンと1対1で対応されていて、他のトークンと区別が付かなくなることはありません。この変換作業もライブラリの仕事です。また、変換後のベクトルの数値をプログラマが眺めても、その意味を理解することはできません。ベクトルの中身は、Transformerが理解できればいいものです。
図3-3: トークン「ランチ」をベクトル化する
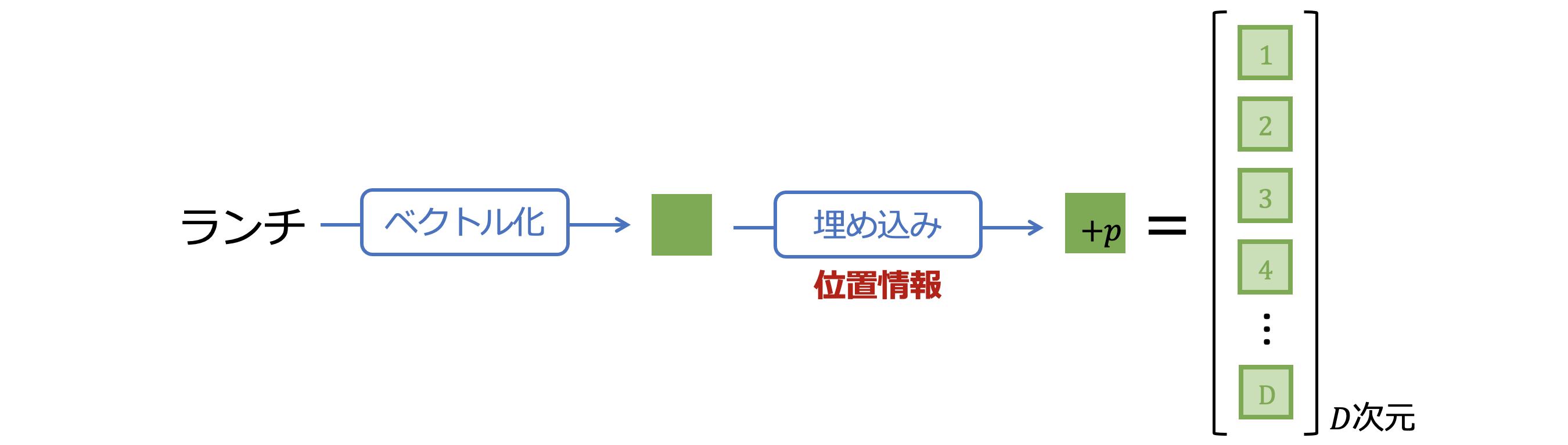
図3-3は、「ランチ」というトークンをベクトル化したイメージです。ここでは、ベクトルを「色つきの 
」で表すことにします。「ランチ」をベクトル化したことをここでは 
と表現しています。ベクトルの次元は$D$で表しています。次元はハイパーパラメータで、Transformerの提案論文では512次元としています。
3.5. ベクトルに位置情報を埋め込む
Transformerはトークンの順番を区別しないそうです。例えば「今日／の／ランチ／は／カレー／だ／。」と「だ／今日／は／。／の／カレー／ランチ」は同じ入力として処理されてしまいます。これを避けるため、トークンの順番を位置情報としてベクトルに埋め込みます。ここで再び「ランチ」というトークンを例にします。
図3-4: トークンの位置情報
「ランチ」は図3-4にあるように、文の先頭から数えて3番目のトークンということになります。したがって「ランチ」のベクトルに3番目であること示す情報を埋め込むことを考えます。シンプルに考えれば先頭からの番号3を埋め込めば良さそうですが、そうは簡単にいかないようです。Transformerの提案論文では、三角関数($\sin$と$\cos$)を利用したやや複雑な位置の表現形式が採用されています。しかしここでは省略し、"トークンのベクトルにトークンの位置を示す情報が埋め込まれる" という理解に留めます。その位置情報の埋め込みのイメージを図3-5に示します。
図3-5: トークンへの位置情報の埋め込み
「ランチ」のベクトルを と表すことにしていました。このベクトルに位置情報を埋め込んだ状態を$+p$の添え字を追加して、 
と表すことにします。これらのベクトルは同じ$D$次元です。
3.6. 入力ベクトルの全体を見る
さて、ここまで1つのトークン「ランチ」のみに注目してきましたが、同じ処理を全てのトークンに対して施します。その結果のイメージを図3-6に示します。
図3-6: 全てのトークンをベクトル化する
各トークンのベクトル を区別させるために色を変えています。ここから先は、ベクトルの違いを色の違いで区別します。入力ベクトルを全てまとめる図3-5となります。
図3-7: エンコーダへの入力ベクトル
3.7. Transformerへの入力
Transformerへの入力準備が整いました。図3-6はTransformerへの入力ベクトルのイメージです。エンコーダへは、ここまで説明してきた「今日のランチはカレーだ」をベクトル化した6色の を列にして入力しています。デコーダへは、すでに得られている翻訳文である "Today's lunch is" を同様にトークン分割・位置情報埋め込みをしたベクトルを3色の で表現し、列ベクトルにして入力しています。
図3-6: Transformerへの入力ベクトル
4. ベクトルが表現力を持つとは
先のセクションで入力の文をトークンに分割して、そのトークンを対応するベクトルへと変換しました。この時点では、Transformerモデルはトークン間の関係を学習していません。せいぜい、それぞれのトークンが他のトークンとは違うようだ、程度の知識しかない状態です。ここから先の自己注意機構・ニューラルネットワークを通じて、個々のトークンのベクトルは他のベクトルとの関係性を学習し、表現力を獲得していきます。ベクトルが表現力を持つとはどういうイメージでしょうか。
次の3つの文章を考えます。
「この高校はサッカーが強い。」
「主催者からの強いメッセージ。」
「地震に強い構造の建物。」
どの文章にも「強い」という形容詞が含まれています。しかしこの「強い」の意味するところは、それぞれの文章によって異なります。「サッカーが強い」は大会での成績を、「強いメッセージ」は一番言いたい事を、「強い構造」は自然災害でも安心であることを示しています。
図4-1: 表現力を持たないトークンのベクトル
図4-1のように、学習前のTransformerモデルはトークンに表現力を持っていないため、「強い」というトークンのベクトルは文脈に関係なく同じ方向・大きさとなっています。
図4−2: 表現力を獲得したトークンのベクトル
次に、学習が完了し、Transformerモデルがベクトルの表現力を持った状態を図4−2に示します。「強い」というトークンのベクトルが、それぞれ違う方向と大きさを持っていることが分かります。これは、元々の「強い」というトークンのベクトルが周辺のベクトルからの情報を受け取って、「（サッカーが）強い」などのそれぞれの位置に変換されていることを示しています。
図4−3: 「強い」と「サッカー」のベクトルの足し算
例えば、図4−3で「この高校はサッカーが強い。」という文章を考えると、「強い」というトークンは「サッカー」と関係性がありそうだとなります。そこで、「強い」ベクトルは「サッカー」ベクトルから関係性を情報として受け取り、「（サッカーが）強い」というベクトルへと変換されるのです。
Transformerでは、このような変換を自己注意機構を用いて全てのトークンに対して自動的に、何通りもの組合せで行います。そうすることで、強力で多様なベクトルの表現力を獲得することが可能です。なお、図では2次元ベクトルで表現力を説明しましたが、実際のGPTモデルでは、768〜2048次元(GPT-4ではそれ以上)の高次元空間で表現の学習が行われているそうです。
5. エンコーダ
5.1. 自己注意機構
ここからは自己注意機構のメカニズムを説明します。前のセクションまでで、文章をベクトル化して入力しました。自己注意機構はこの入力ベクトルを受け取って処理を進めます。ところで、エンコーダとデコーダともに、入力直後にそれぞれの自己注意機構が配置されています。この記事ではどちらの自己注意機構も同じものとしていますので、ここからはエンコーダの自己注意機構について説明します。
5.1.1. 自己注意機構の概要
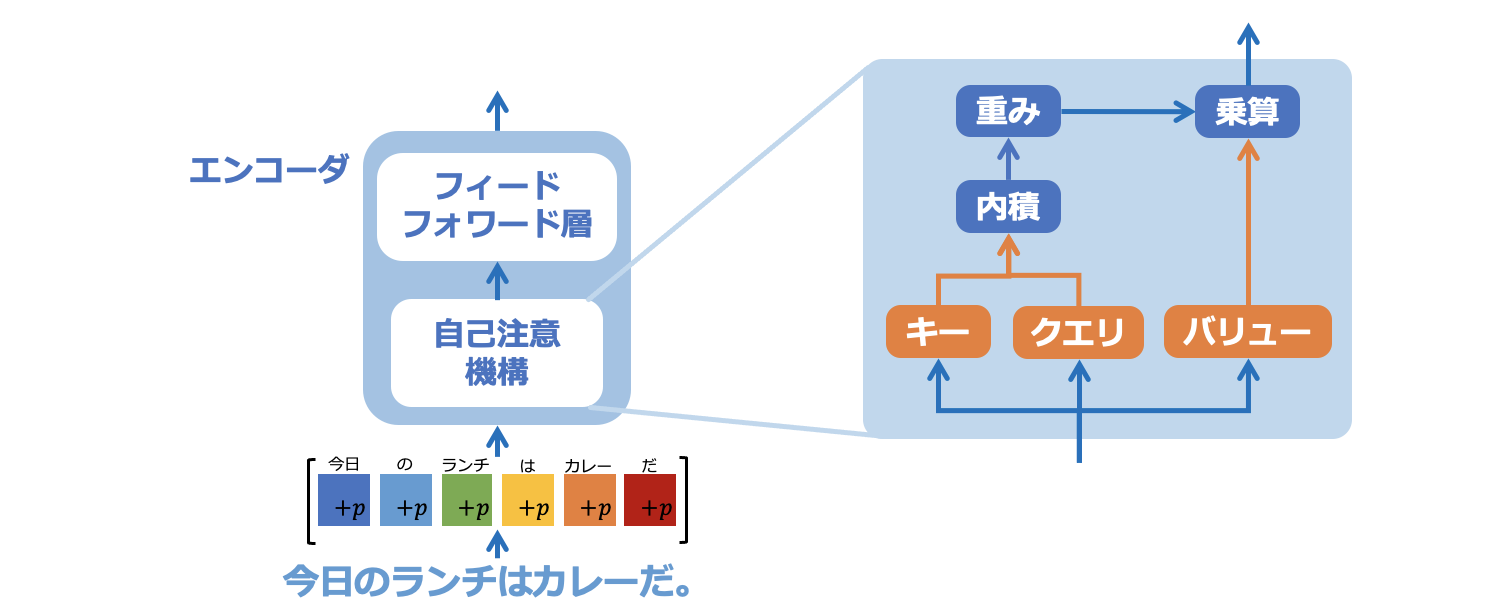
図5−1は自己注意機構の内部の計算過程をイメージで説明したものです。まず、入力ベクトルはキー、クエリ、バリューという3つの別のベクトルに変換されます。
図5−1: 自己注意機構の概略図
次に全てのキーとクエリの組合せで内積が計算されます。その結果をソフトマックス関数で正規化します。正規化された値は重み(アテンション・ウェイト)と呼ばれ、トークン間の関連性を示しています。重みはバリューと乗算され、エンコーダからの出力となります。ニューラルネットワークは、それぞれのベクトルの表現力をさらに高めます。
概略として文章にしてしまうと単純な仕組みですが、詳細はもう少し複雑です。次のセクションから詳しい計算方法と、それで何をしているのかについて見ていきます。
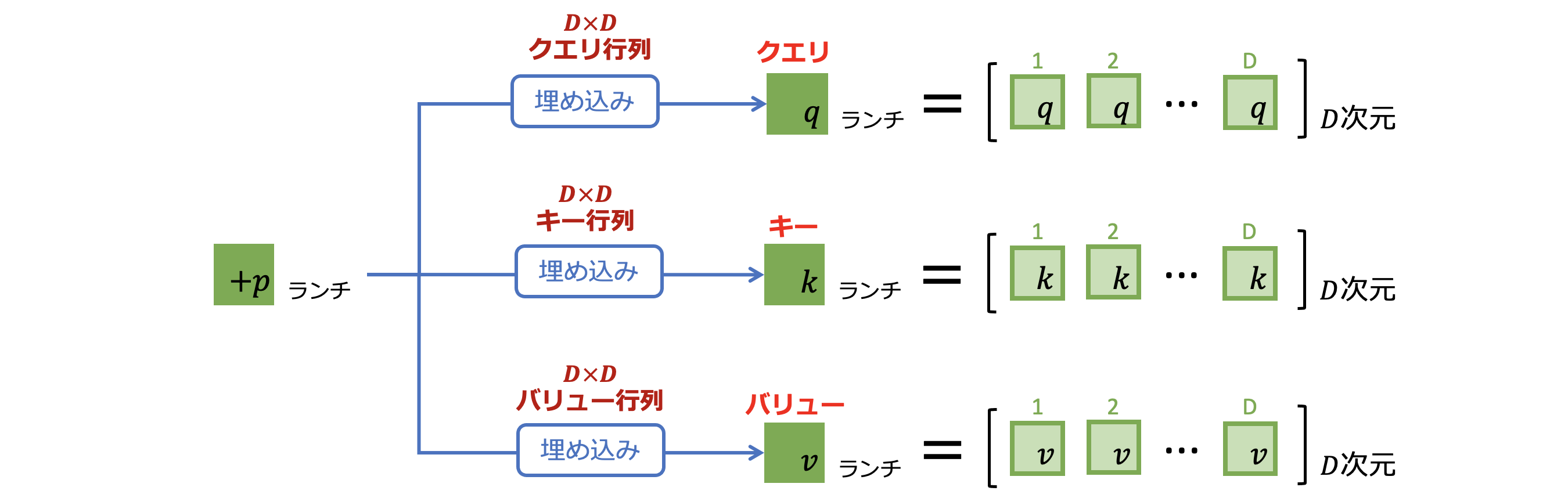
5.1.2. キー・クエリ・バリューの作成
まず、図5-2で「ランチ」というトークンの入力ベクトルを例にします。ここまでの説明通り、トークンはベクトルに変換され、位置情報を埋め込まれて という形式のベクトルになっています。これとキー行列と呼ぶ行列をかけ算することでキーを作成しています。キーはこの図にあるように 
で表示することにします。
図5-2: 「ランチ」ベクトルからキーの作成
少し込み入った話になりますが、 は$D$次元のベクトルで、キー行列は$D \times D$の行列と定義します。$D$次元のベクトルと$D \times D$の行列のかけ算なので、 も$D$次元のベクトルとなります。
続いてクエリとバリューを作成します。図5-3にあるように作成方法はキーと同じで、クエリの作成にはクエリ行列を、バリューの作成にはバリュー行列をかけ算して作成しています。
図5-3: 「ランチ」ベクトルからクエリとバリューの作成
「ランチ」トークンに対応するベクトルのキー・クエリ・バリューを計算しました。この計算を他のトークンのベクトルにも適用して、全てのトークンのベクトルに対してキー・クエリ・バリューを求めます。
5.1.3. アテンション・ウェイトの計算
アテンション・ウェイトの計算が、Transformerの自己注意機構における最もコアとなる部分です。まずはどのような計算をしているか見てから、その計算が何を意味するのか見てみましょう。
5.1.3.1. 内積と関連性スコア
内積とはベクトル同士のかけ算のことです。内積を計算した結果の意味するところは、ベクトル同士の関連性です。同じ方向を向いたベクトル同士の内積値は大きくなり、関連性が高いと判断されます。逆に違う方向を向いたベクトル同士の内積値は小さくなり、関連性が低いと判断されます。
そこで、この原理を応用してトークンのベクトル同士の内積を計算することで、お互いの関連性をスコアとしてを求めてみます。例として「ランチ」と「カレー」を見てみましょう。内積はトークンのクエリとキーを利用して、関連性スコア 
は図5-4で計算されます。
図5−4: 関連性の計算式
ベクトルを表す の色は、入力ベクトルのトークンに対応しています。ここでは 
は「ランチ」のクエリ、 
は「カレー」のキーを表していることになります。ちなみに、 の肩に乗った$T$の記号はベクトルの転置を表していて、これは同じ方向のベクトルの内積を計算するときのお決まりとなっています。また、$\sqrt{D}$はベクトルの次元数$D$が大きくなると、内積の計算値自体が大きくなってしまうことを防止する役目を果たしています。
図5-5: 関連性スコアの濃淡
さて、内積を計算することはベクトル同士の関連性スコアを計算することでした。従って、「ランチ」のクエリと「カレー」のキーの内積である は「ランチ」と「カレー」の関連性スコアを表しています。実際、関連性スコアの値は実数のスカラーなのですが、ここは の灰色の濃淡で表現することにします。図5-5にあるように、灰色が濃いと関連性スコアは高いことを示し、灰色が薄くなると関連性スコアは低くなることを表しています。つまり、灰色が濃いほど2つのトークンは文脈上の関係が強いということになります。なお、計算結果の色の濃淡は実際の計算値ではありません。あくまでもイメージとして捉えてください。
5.1.3.2. トークン同士の関連性スコア
さきほどは「ランチ」と「カレー」の組合せだけで関連性スコアを計算しましたが、ここで全てのトークンの組合せに拡張してみます。
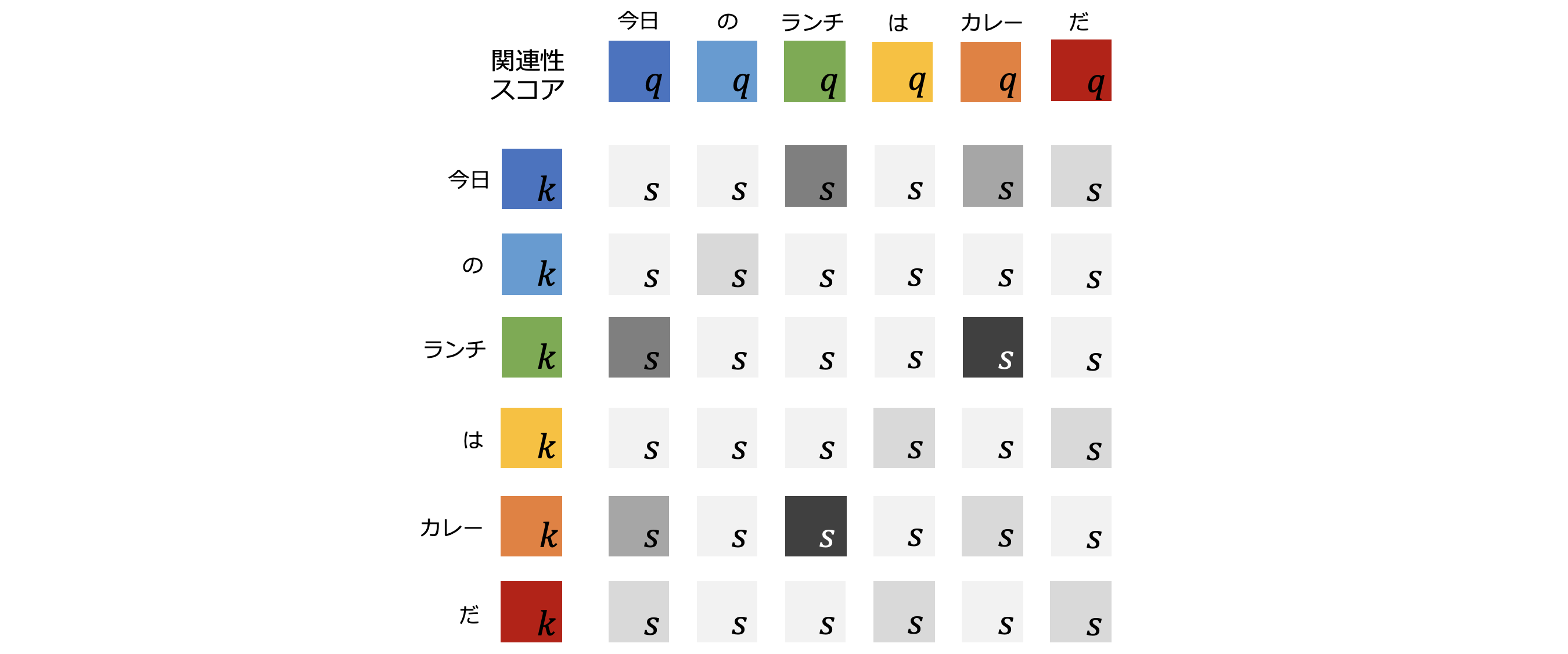
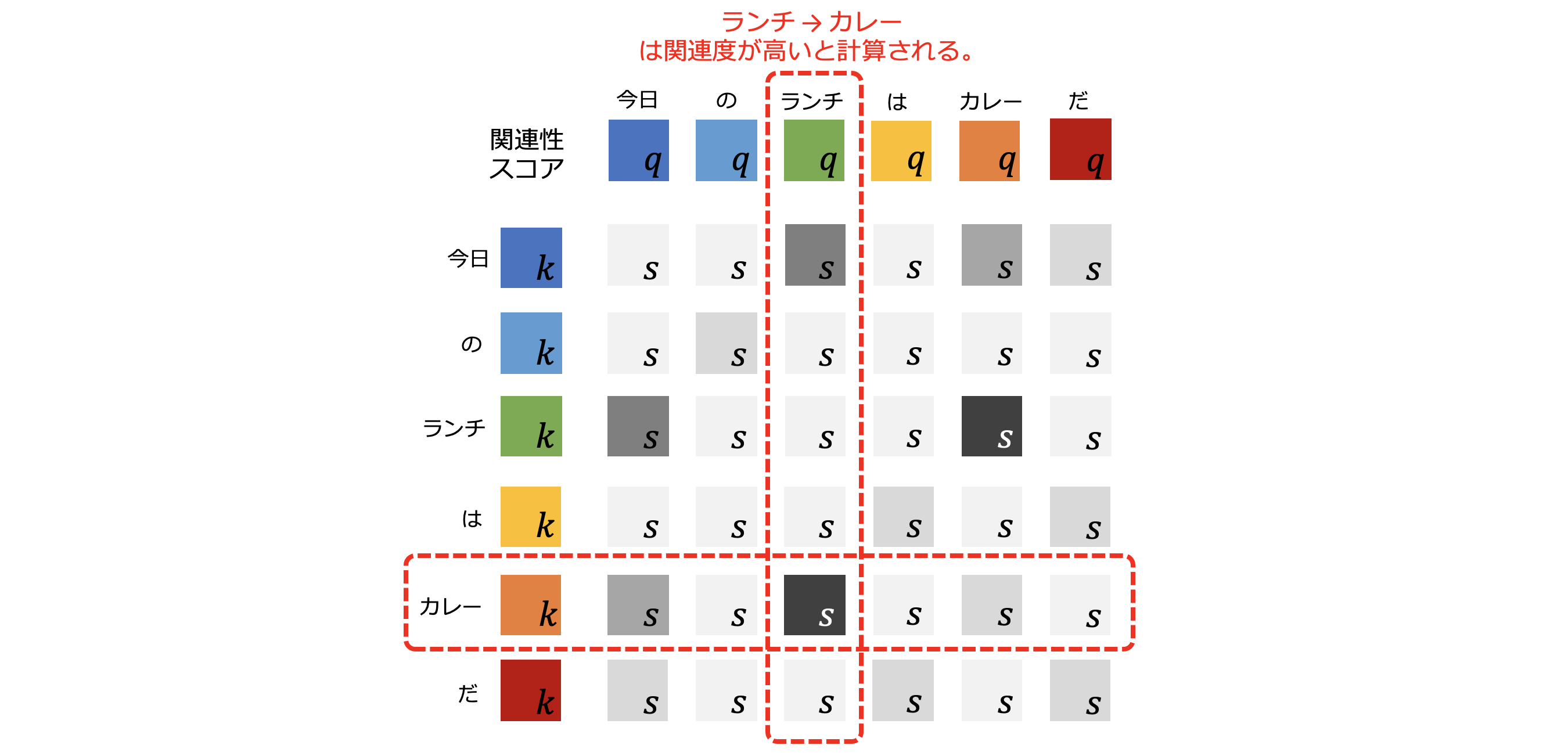
図5-6: 全てのトークン同士の関連性スコアを表した表
つまり、図5-6のように「今日／の／ランチ／は／カレー／だ」の全てのクエリとキーで関連性スコアを計算します。関連性スコアの灰色の は色が濃いほど高い関連性を示すものでした。
図5-7: 「ランチ」のクエリと他のキーとの関連性スコア
ここで、図5-7のように「ランチ」のクエリ に注目してみます。「ランチ」のクエリ と「カレー」のキー の組合せの関連性スコアの色が濃いので、この2つのトークンの関連性スコアは高そうです。逆に「ランチ」のクエリ に対して他のトークンのキーの組合せでは関連性が低そうです。このように、「ランチ」と他の全てのトークンとの関連性スコアを抽出することができました。
ところで、内積を計算するなら、わざわざベクトルをクエリ・キーに変換しなくても、直接トークンのベクトル同士の内積を計算すればいいと思うかもしれません。しかしトークンのベクトル同士で内積を計算すると、同じトークンでは同じベクトルでの内積となってしまい、当然その値は大きくなります。同じトークン同士に関連性スコアが集中するのを避けるために、クエリ・キーに変換しています。また、キー・クエリ・バリューの変換は、より適切な組合せで関連性スコアを抽出できるように調整する役目もあります。
5.1.3.3. 関連性スコアの埋め込み
図5-8: 出力ベクトルの計算①
続いて、図5-8でこの関連性スコアを用いて自己注意機構からの出力ベクトルを求めます。再び、「ランチ」と「カレー」に注目します。
「ランチ」のクエリ と「カレー」のキー で内積を計算して関連性スコア 
を求めることは説明しました。ここでは、 と「カレー」のバリュー 
をかけ算して、ベクトル 
を計算しています。これは 「ランチ」トークンから見た「カレー」トークンの関連性スコアを含んだベクトル と解釈することができます。つまり、「ランチ」トークンにとって「カレー」トークンは、文脈を理解する上でどれだけ重要か？ という情報です。
図5-9: 出力ベクトルの計算②
次に、図5-9で 「ランチ」トークンから見た関連性スコアを含んだベクトルを、全てのトークンに対して適用します。「ランチ」トークンから見た全てのトークンとの関連性スコアを含んだベクトルが各トークンの$a'$として出力されました。
さらに、各トークンの $a'$ を全て加算することでベクトル 
を得ます。これが「ランチ」トークンのベクトルを自己注意機構に入力したときの出力ベクトルです。
5.1.4. 自己注意機構からの出力
図5-9では「ランチ」トークンのみの出力ベクトルを求めていますが、この操作を全てのトークンに対して実施します。
図5-10: エンコーダへの入力と出力のベクトル
全てのトークンに対して出力ベクトルを求めると、自己注意機構からの出力は図5-10のようなベクトル列となります。これは入力したベクトル列と同じサイズのベクトル列です。
5.1.5. 自己注意機構の気持ち
自己注意機構では、キー・クエリ・バリューのベクトルが大きな役割を担っているということになります。キー・クエリ・バリューのベクトルは、元々はあるトークンのベクトルを変換したものでした。したがって、キー・クエリ・バリューと名前は違えど、どれも同じ1つのトークンを示していることになります。
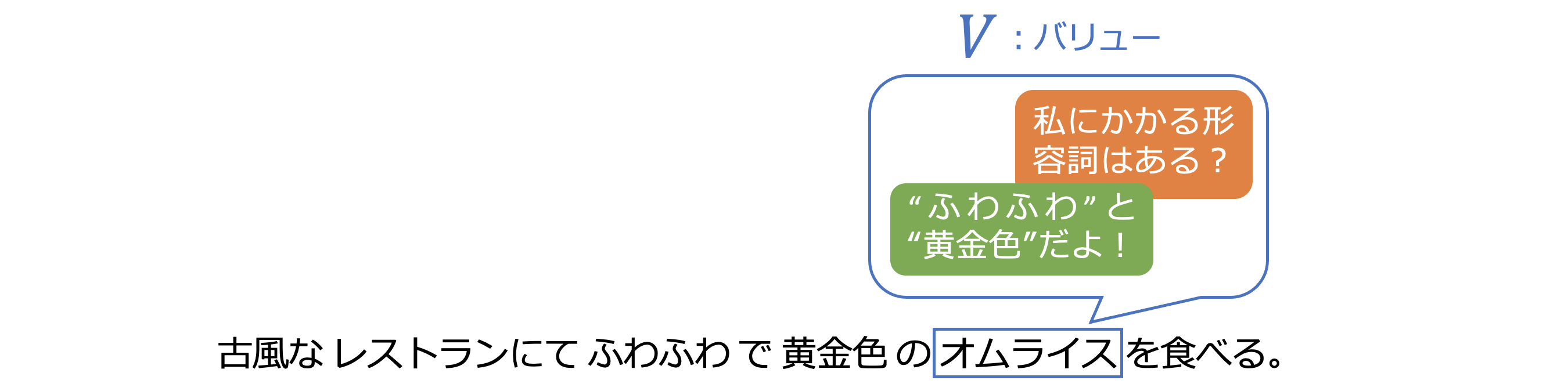
ここで例として「古風なレストランにてふわふわで黄金色のオムライスを食べる。」という文を考えてみます。
図5−11: クエリ・キーの関係
クエリベクトルは、そのトークンから他のトークンへの問合せに相当します。図5-11のように、「オムライス」トークンが他のトークンに対して「私にかかる形容詞はある？」という問合せがクエリです。すると、「ふわふわ」と「黄金色」というトークンがそれぞれ「あるよ！ここだよ！」と返事をします。この返事がキーに相当します。
もちろん、先ほどまでに見てきたようにクエリによる問合せは、全てのトークンに対して行います。「ふわふわ」と「黄金色」のように自信を持って答えるトークンもあれば、あまり自信のない答え方をする他のトークンもあるでしょう。したがって、自信を持って答えるトークンの重要度に重きを置き、そうでないトークンからは影響を受けないよう調整する必要があります。
例えば「古風な」という形容詞もありますが、これは「レストラン」にかかっているので、「オムライス」クエリへのキーにはなっていません。
図5−12: バリューが持つ情報
バリューベクトルは、そういった様々な問合せと回答と重要度の情報をひとまとめにして持っているベクトルです。図5-12にあるように、「オムライス」のバリューベクトルは、さきほどの形容詞に関する他のトークンとの情報を持っています。
5.2. フィードフォワード層
フィードフォワード層は、エンコーダの自己注意機構のあとに配置されています。
5.2.1 フィードフォワード層の構造
フィードフォワード層は入力層に加えて、1つの中間層と出力層をもつ、2層の順伝播型ニューラルネットワークです。中間層には活性化関数が配置されており、ReLu関数もしくはGELU関数が利用されるようです。
エンコーダの自己注意機構から出力された各トークンのベクトル列は、フィードフォワード層へと入力されます。そのうち「ランチ」ベクトル がフィードフォワード層へ入力されるイメージを図5-13に示しました。 は$D$次元あるので、フィードフォワード層の入力次元も$D$次元です。これが中間層では$D_m$次元へと拡張されます。中間層の次元数は入力層の4倍に設定されることが一般的なようです。GPTモデルの初期バージョンでは、入力ベクトルの次元数は768次元とされているので、中間層では3072次元にもなります。一方、出力層では入力と同じサイズの$D$次元へと集約され、 
として出力されます。
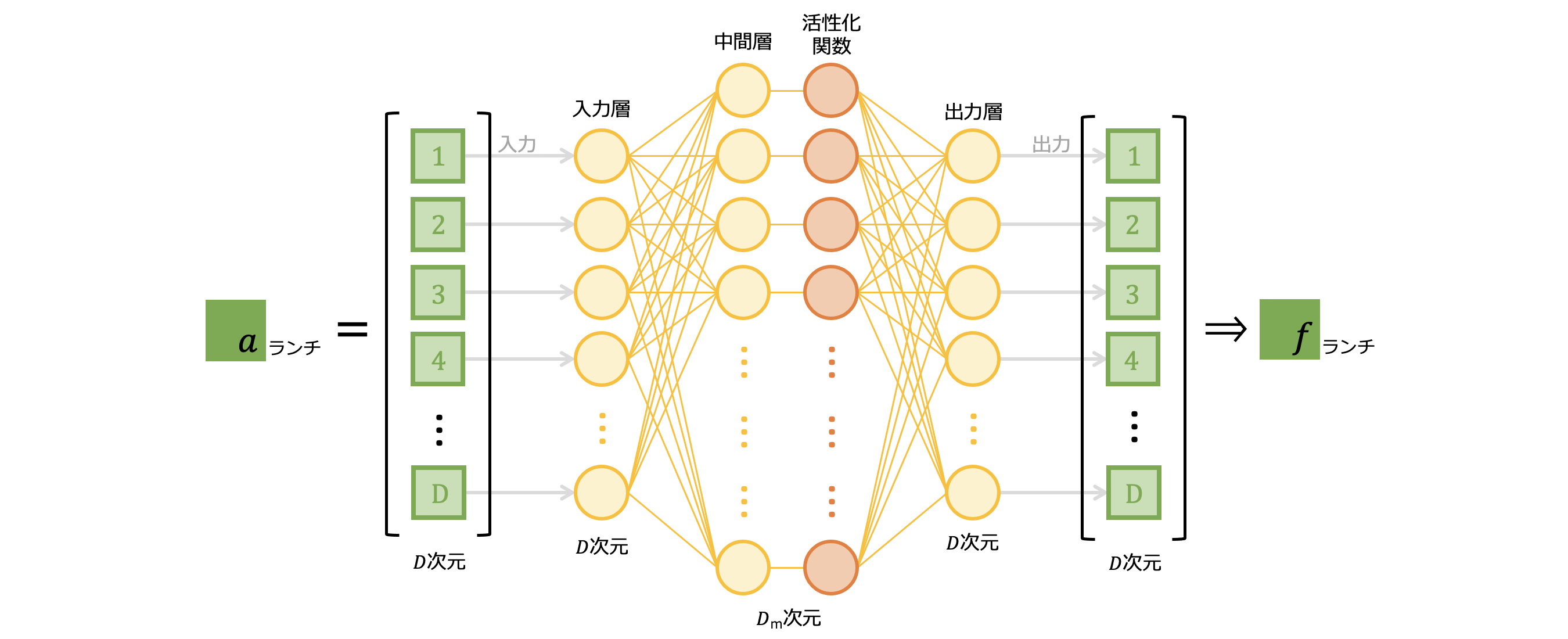
図5-13: 「ランチ」ベクトルのフィードフォワード層への入力
中間層で入力層の4倍もの次元があるため、そのパラメータ数は莫大なものになります。全てのフィードフォワード層のパラメータで、Transformer全体のパラメータ数の3/4を占めているそうです。Transformerの提案論文のタイトルは "Attention is All You Need" となっていますが、パラメータ数だけ見ればフィードフォワード層が最も大きなウェイトを占めていることになります。実際、Transformerが自己注意機構のみになってしまうと、ベクトルの表現力は著しく低くなってしまうそうです。
フィードフォワード層で情報がどのように扱われているのか明らかになってはいないようです。ただ、パラメータ数の大きさから、大規模言語モデルの持つ大半の知識がこの層に記憶されていると考えることができそうです。
また、自己注意機構ではトークン相互で計算が行われていましたが、フィードフォワード層では図5-13に示したように「ランチ」であれば「ランチ」トークンのみで学習が完結していて、他のトークンから干渉を受けることはありません。
5.2.2. フィードフォワード層からの出力
図5-14: フィードフォワード層からの出力
全てのトークンに対してそれぞれ個別にフィードフォワード層で学習が行われ、フィードフォワード層から出力されます。図5-14で各出力ベクトルは$f$という添え字を付けて表現しています。
5.3. エンコーダからの出力
図5-15: エンコーダからの最終的な出力
図5−15のように、フィードフォワード層からの出力ベクトルがそのまま自己注意機構からの出力ベクトルとなります。添え字が$f$から$o$に変わっていますが、ベクトルの中身は同じです。
6. デコーダ
6.1. 自己注意機構
図6−1: デコーダの自己注意機構への入力と出力
デコーダでも、図6−1にあるように入力ベクトルはエンコーダと同様に自己注意機構を通過します。処理内容は自己注意機構と同じで、出力もトークンの相互の関連性度合いを学習したベクトルとなっています。
6.2. 交差注意機構
交差注意機構の構造は、自己注意機構とほぼ同じです。すなわち、入力ベクトルからキーベクトル・クエリベクトル・バリューベクトルを作成し、アテンション・ウェイトを計算した後、出力のベクトルを算出します。交差注意機構の場合、入力ベクトルはエンコーダとデコーダのベクトルそれぞれから入力されることが自己注意機構との違いです。
6.2.1. 交差注意機構の演算
図6-2: 交差注意機構への入力
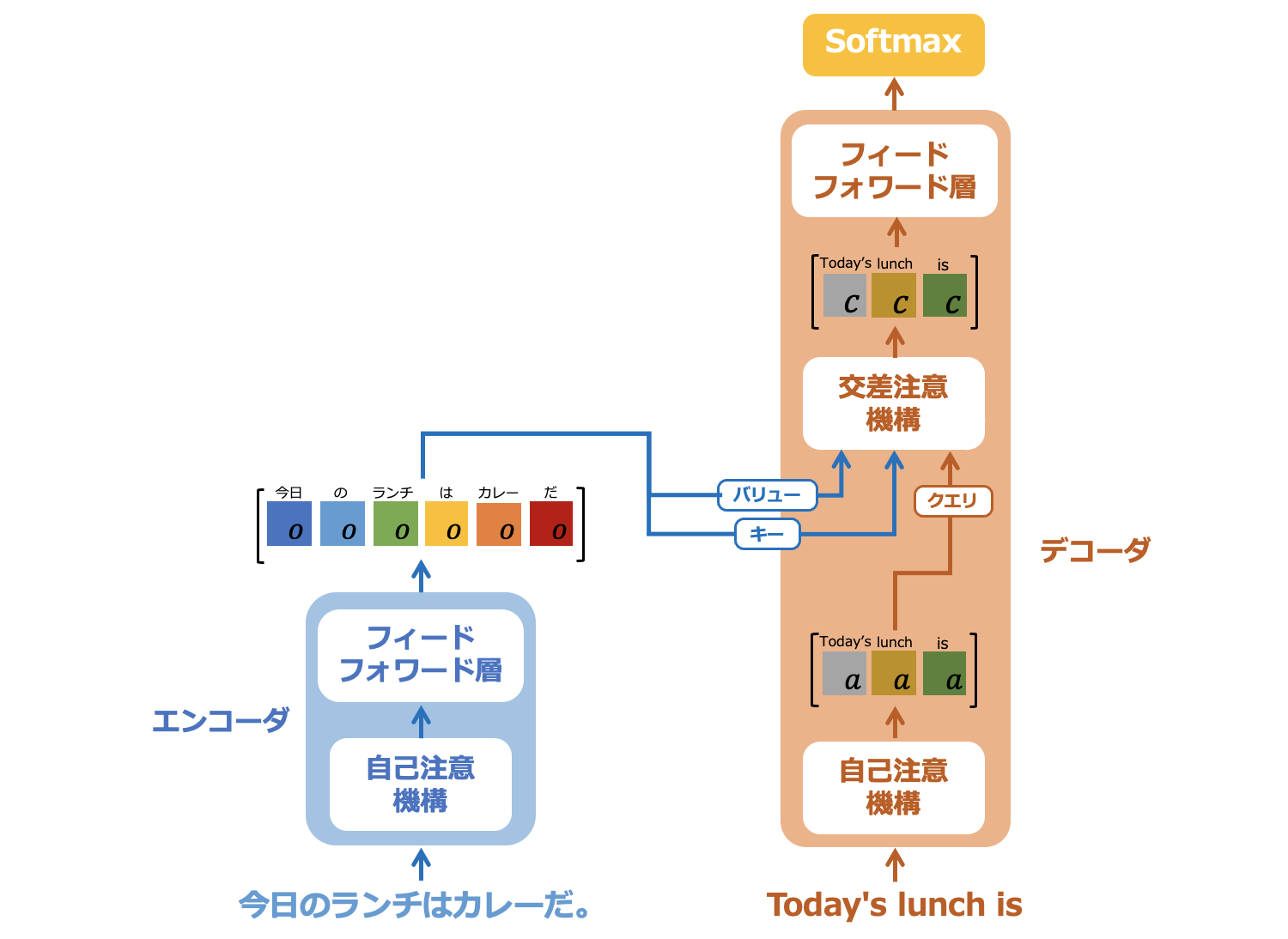
図6−2にあるように、交差注意機構も自己注意機構と同様に、クエリ・キー・バリュー ベクトルが入力されます。ただし、デコーダの自己注意機構からの出力ベクトルをクエリに変換し、エンコーダからの出力ベクトルをキー・バリューに変換するという、やや複雑な入力となっています。
図6-3: クエリ・キー・バリュー ベクトルへの変換イメージ
図6-3にベクトル変換のイメージを示しました。デコーダの自己注意機構からの出力は、"Today's lunch is" に対応するベクトル列で、これらはクエリベクトルに変換されます。この図では、クエリ行列を使って "lunch"トークンのベクトル 
が、クエリベクトル 
に変換されています。
エンコーダからの出力は、「今日のランチはカレーだ」に対応するベクトル列で、これらはキーベクトル・バリューベクトルに変換されます。この図では、キー行列・バリュー行列を使って「カレー」トークンのベクトル 
が、キーベクトル 
とバリューベクトル 
に変換されています。
図6-4: 関連性の計算式
キー・クエリ・バリューのベクトルに変換されれば、これらのベクトルの計算は自己注意機構と同じです。エンコーダから出力された原文「今日／の／ランチ／は／カレー／だ」と、デコーダの自己注意機構から出力された翻訳文 "Today's／lunch／is"の各トークンのベクトル同士の関連性スコアを内積を計算して算出します。計算式のイメージを図6-4に示しました。
図6-5: 原文と翻訳文のトークン同士の関連性スコアを表した表
自己注意機構と同じように、各トークンの関連性スコア$s$の計算結果のイメージを図6-5にしてみました。こちらも、関連性スコア$s$の色が濃ければ関連が高いと判断されます。
図6-6: 出力ベクトルの計算
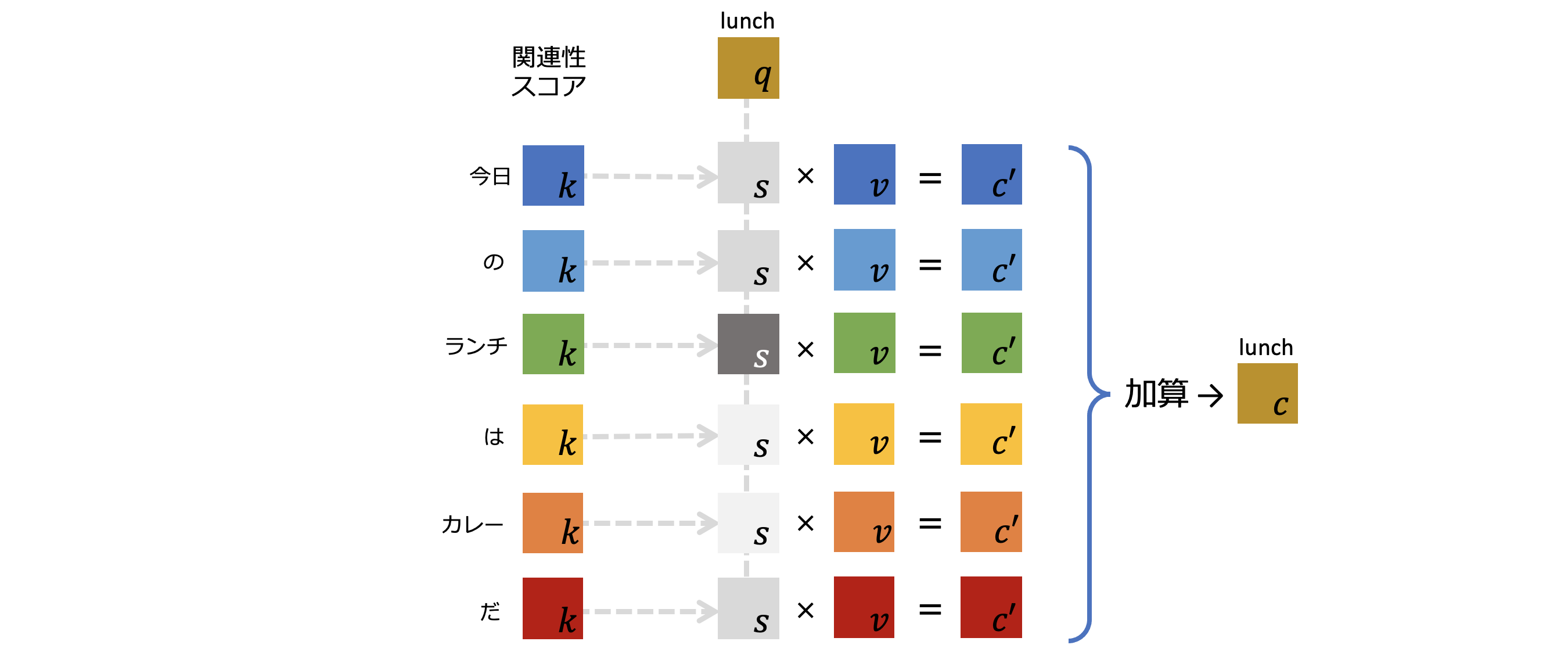
図6-6では、"lunch"トークンから見た関連性スコアを含んだベクトルを、全てのトークンに対して適用します。"lunch"トークンから見た全てのトークンとの関連性スコアを含んだベクトルが各トークンの$c'$として出力されました。
さらに、各トークンの$c'$を全て加算した 
が、"lunch"トークンの交差注意機構からの出力となります。
6.2.2. 交差注意機構からの出力
図6-7: 交差注意機構からの出力
図6-6では"lunch"トークンのみの出力ベクトルを求めていますが、この操作を全てのトークンに対して実施します。全てのトークンに対して出力ベクトルを求めると、結果的に入力したベクトル列と同じサイズのベクトル列が出力されます。デコーダの自己注意機構からの入力と出力イメージをまとめたのが図6−7です。
6.3. フィードフォワード層
デコーダのフィードフォワード層は、エンコーダのフィードフォワード層と同じ構造です。すなわち、入力層に加えて1つの中間層と出力層をもつ、2層の順伝播型ニューラルネットワークです。デコーダでのフィードフォワード層の役割は、エンコーダのそれと同様に膨大な知識情報を蓄積することにあるようです。
7. Transformerからの出力ベクトル
図7−1: Transformerからの出力ベクトル
Transformerからの出力をまとめると、図7-1となります。
図7-2:Transformerからの出力ベクトル
ここまでのベクトル計算で、Transformerからの出力ベクトルは、"Today's"の 
、"lunch"の 
、"is"の 
でした。各ベクトルは図7−2にあるように、$D$次元の縦ベクトルです。ちなみに、入力のベクトルも$D$次元だったので、同じサイズのベクトルが出力されることになります。
8. 次のトークンの予測
Trasformerからの出力ベクトルをもとに、入力した文章に続く次のトークンを予測します。その前に、このTransformerモデルが学習した全てのトークンの集合$V$を考えます。$V$の中身は $e_1, e_2, e_3, e_4, \dots$ となっていて、 番号の付いた$e$の1つ1つが学習したトークンに対応しています。例えばGPT-1では、約7,000冊の書籍を学習データとしたとのことなので、7,000冊分に登場したトークンが重複なく$V$に含まれていることになります。
図8-1: 全ての学習済みトークンの集合$V$
各ベクトル$e$は$D$次元で、これらを全てまとめると図8-1のようになります。次のトークンの予測にはこの$V$の全てのベクトルと、Transformerからの出力ベクトルで内積を計算します。
しかも、Transformerからの出力ベクトルは、予測したいトークンの直前のトークンである"is"のベクトル のみを使います。残りの出力ベクトルは必要ないのかと言うことになりますが、必要ありません。なぜなら自己注意機構・交差注意機構によって、 には関連するトークンからの情報をすべて受け取っている状態だからです。
図8-2: トークン同士の内積計算
$V$に含まれる全てのトークンベクトルと、"is"の出力ベクトル の内積を計算しているイメージを図8−2にまとめました。なお、ここではソフトマックス関数も通過していて、内積値は$(0，1)$の範囲に収まっていることとします。
内積はベクトル同士の関連性を表していて、その値が大きいほどお互いの関連性が高いことを示しているのでした。$V$に含まれるほとんどのトークンとの内積値は$0$に近い数値、つまり"is"との関連性がないという結果になります。
内積値の最大値を探したところ、$n$番目のトークンベクトル$e_n$との値が最大となったとします($0.8658$)。すなわち、$e_n$が推論された次のトークンということになります。その$e_n$に対応するトークンが、ここでは"curry"である、ということになります。
9. さらに詳しく
ここまで、私が理解した範囲でTransformerモデルの仕組みを説明してきました。
図9−1: Transformerの本当の姿
実は、図9−1に示すように、Transformerモデルはもっと複雑な構造をしています。ここまでの説明で言及できなかった点を以下に並べました。
9.1. エンコーダ・デコーダブロック
エンコーダとデコーダはそれぞれエンコーダブロック・デコーダブロックと呼ばれ、L個のブロックが直列に接続された構造をしています。L個のブロックにはそれぞれ独立したパラメータがあり、より多様な知識を学習することが可能です。
9.2. マルチヘッド注意機構
自己注意機構の次元を$M$個に分割し、それらを並列して学習させます。これをマルチヘッド注意機構と呼びます。$M$個に分割されているので、全体のパラメータ数に変化はありません。具体的には、入力の$D$次元が$D/M$次元になります。マルチヘッド化によって、品詞の表現力がより強化されるとのことです。
9.3. ショートカットと層正規化
マルチヘッド注意機構やフィードフォワード層を迂回するような矢印が引いてあります。これは処理後のベクトルに処理後のベクトルを加算していることを示しています。また、層正規化によってベクトルを正規化しています。
10. 参考文献
ここまで読んでいただき、ありがとうございます。こんなに書いといてなんですが、私もちゃんと理解できているのか不安です。きちんと勉強したい方には、以下の参考文献をおすすめします。
[1]はTransformerの提案論文です。[2]は[1]の数学的なアルゴリズムが解説されています。この記事の内容はほぼ[2]の理解に依るものです。[3]はHugging FaceというTranformerモデルライブラリの解説書ですが、[1]のアルゴリズムの解説もあります。[4][5]はYouTube上の解説動画です。この動画は東京大学の有志学生団体3Blue1BrownJapanによる公式和訳版で、英語のオリジナルは3Blue1Brownという数学のチャンネルです。数式の意味やイメージを理解するのにかなり役に立ちました。
[1] "Attention is all you need", Ashish Vaswaniら, 2017
[2] "大規模言語モデル入門", 山田育矢ら, 技術評論社, 2023
[3] "機械学習エンジニアのためのTransformers ―最先端の自然言語処理ライブラリによるモデル開発", Lewis Tunstallら, オライリージャパン, 2022
[4] "GPT解説2 アテンションの仕組み(Attention,Transformer)|Chapter6,深層学習", https://www.youtube.com/watch?v=j3_VgCt18fA, YouTube
[5] "LLMはどう知識を記憶しているか|Chapter7,深層学習", https://www.youtube.com/watch?v=mmWuqh7XDx4, YouTube