はじめに
本記事は簡単な線形回帰モデルのベイズ推定に関するものである。具体的にはギブス・サンプリングを用いてマルコフ連鎖モンテカルロ法(通称:MCMC)をpythonで実装を行なった。pythonでのMCMCの実行は、pymcというモジュールによるものが有名であるが、今回は敢えてpymcを用いずにnumpyとscipyのみで実装を試みた。この記事を書くにあたって古澄さんの『ベイズ計算統計学』(朝倉書店)を大いに参考にした。
理論
実装の前に簡単ではあるが理論を振り返る。推定したい線形回帰モデルは
y_i=\boldsymbol{x}_{i}'\boldsymbol{\beta}+u_i, \ \ u_i\sim N(0,\sigma^2) \ \ (i=1,\cdots,n)
と表される($y_i$は非説明変数、$\boldsymbol{x}$はk×1の説明変数ベクトルで、$u_i$は平均0、分散$\sigma^2$の正規分布に互いに独立に従う誤差項を表す)。このとき$y_i$は平均$\boldsymbol{x}_{i}^{'}\boldsymbol{\beta}$、分散$\sigma^2$の正規分布に従うことより、尤度関数は
\begin{align}
f(\boldsymbol{y} \ | \ \boldsymbol{\beta},\sigma^2) &= \prod_{i=1}^{n}\frac{1}{(2\pi\sigma^2)^{1/2}}\mathrm{exp}\left\{-\frac{(y_i-\boldsymbol{x}_{i}'\boldsymbol{\beta})^2}{2\sigma^2}\right\} \\
&\propto \left(\frac{1}{\sigma^2}\right)^{n/2}\mathrm{exp}\left\{-\frac{\sum_{i=1}^{n}(y_i-\boldsymbol{x}_{i}'\boldsymbol{\beta})^2}{2\sigma^2}\right\}
\end{align}
となる。
またパラメーターの事前分布については、
\boldsymbol{\beta} \sim N(\boldsymbol{\beta}_0,\boldsymbol{B}_0), \ \ \sigma^2 \sim IG\left(\frac{n_0}{2},\frac{s_0}{2}\right)
であると仮定する(ただしIGは逆ガンマ分布を意味する)。したがって、以上の尤度と事前分布にベイズの定理を適用すると、事後分布は
\pi(\boldsymbol{\beta},\sigma^2 \ | \ \boldsymbol{y}) \propto \left(\frac{1}{\sigma^2}\right)^{n/2}\mathrm{exp}\left\{-\frac{\sum_{i=1}^{n}(y_i-\boldsymbol{x}_{i}'\boldsymbol{\beta})^2}{2\sigma^2}\right\}\mathrm{exp}\left\{-\frac{1}{2}(\boldsymbol{\beta}-\boldsymbol{\beta}_0)'\boldsymbol{B}_{0}^{-1}(\boldsymbol{\beta}-\boldsymbol{\beta}_0)\right\}\left(\frac{1}{\sigma^2}\right)^{n_0/2+1}\mathrm{exp}\left(-\frac{s_0}{2\sigma^2}\right)
となる。
さて、事後分布のカーネルは無事導出できたが上の式の積分計算は解析的には行えないので、事後分布の基準化定数は計算することができない(だからこそ、MCMCを用いてのサンプリングが必要となる)。そこでギブス・サンプリングによって事後分布に従う乱数をうまく生成して、所望の分布の性質を分析していくのだが、ギブス・サンプリングを行うためにはそれぞれのパラメーターの完全条件付き分布を導出せねばならない。これは先ほど導出した事後分布のカーネルから計算することができるがその過程は煩雑なので省略して結果のみを示す(詳しくは各自『ベイズ計算統計学』(朝倉書店)等を参考にされたい)。それぞれのパラメーターの完全条件付き分布は
\begin{align}
\pi(\boldsymbol{\beta} \ | \ \sigma^2,\boldsymbol{y}) &= N(\hat{\beta},\hat{\boldsymbol{B}}) \\
\pi(\sigma^2 \ | \ \boldsymbol{\beta},\boldsymbol{y}) &= IG\left(\frac{n+n_0}{2},\frac{\sum_{i=1}^{n}(y_i-\boldsymbol{x}_{i}'\boldsymbol{\beta})^2)+s_0}{2}\right)
\end{align} \\
ただし、
\hat{\boldsymbol{B}}^{-1}=\sum_{i=1}^{n}\frac{\boldsymbol{x}_i\boldsymbol{x}_i'}{\sigma^2}+\hat{\boldsymbol{B}}_{0}^{-1}, \ \ \hat{\boldsymbol{\beta}}=\hat{\boldsymbol{B}}\left(\sum_{i=1}^{n}\frac{\boldsymbol{x}_iy_i}{\sigma^2}+\hat{\boldsymbol{B}}_{0}^{-1}\boldsymbol{\beta}_0\right)
である。この完全条件付き分布から逐次交互にサンプリングしていけば良い。
pythonによる実装
擬似データを生成して、そのデータからベイズ推定を行い結果の分布が元のパラメーターに近づくか検証を行う。非常に簡単であるがギブス・サンプリングのpythoコードは以下の通り。
import numpy as np
from numpy.random import normal, multivariate_normal
from scipy.stats import invgamma
import matplotlib.pyplot as plt
## 擬似データの生成
alpha = 2.5
beta = 0.8
sigma = 10
data = 100
x = np.c_[np.ones(data), rand(data) * data]
y = 2.5 * x[:,0] + 0.8 * x[:,1] + normal(0, sigma, data)
plt.plot(x[:,1],y,'o')
## ギブス・サンプリング
# burn inの回数とサンプリング数を指定
burnin = 10000
it = 2000
beta = np.zeros([burnin + it, 2])
sigma = np.zeros(burnin + it)
B_hat = np.zeros([2,2])
beta_hat = np.zeros(2)
sum1 = np.zeros([2,2])
sum2 = np.zeros(2)
# ハイパーパラメーターの指定
beta0 = np.array([0,0])
B0 = np.array([[1, 0],[0,1]])
n0 = 2
s0 = 2
# 初期値の設定
beta[0,0] = 1
beta[0,1] = 1
sigma[0] = 1
for i in range(data):
sum1[0,0] += x[i,0] ** 2
sum1[0,1] += x[i,0] * x[i,1]
sum1[0,1] += x[i,0] * x[i,1]
sum1[1,1] += x[i,1] ** 2
sum2[0] += x[i,0] * y[i]
sum2[1] += x[i,1] * y[i]
for i in range(burnin + it - 1):
B_hat = np.linalg.inv(sum1/sigma[i] + np.linalg.inv(B0))
beta_hat = B_hat @ (sum2/sigma[i] + np.linalg.inv(B0) @ beta0)
beta[i+1,:] = multivariate_normal(beta_hat, B_hat)
sigma[i+1] = invgamma.rvs((data+n0)/2,(np.dot(y-beta[i,0]*x[:,0]-beta[i,1]*x[:,1], y-beta[i,0]*x[:,0]-beta[i,1]*x[:,1])))
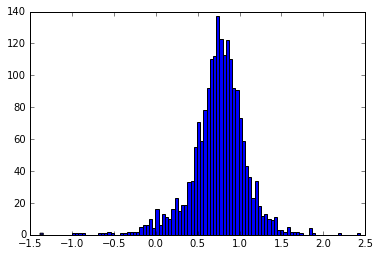
サンプリングの結果、betaのヒストグラムは以下のようになった。
MAP推定量は最初に設定した値である0.8に近づいている様子がうかがえる。やったぜ。
(細かい部分はまた後で追記します)