単回帰分析
単回帰分析で用いる数式の基本は、次のとおり。
$$\hat{y} = a(x - \bar{x}) + \bar{y}$$
入力値$x$に対して、予測したい結果$\hat{y}$を出力するのが、単回帰分析となる。予測したい場合、必要なデータとしては、$x$$i$と$y$$i$の生のデータが必要になる。それら生のデータをもとに、中心化を経て、傾き$a$を求める。求めた傾き$a$と生のデータ$x$$i$と$y$$i$を用いることで、単回帰分析で結果を予測することができる。
例えば、部屋の広さ$x$に対して、部屋の家賃$\hat{y}$を推測することができるようになる。
ただし生のデータ$x$$i$を使用していた場合で、その範囲外の入力値$x$をもとに、予測した結果$y$は正しい予測結果とはならない。これは内挿と外挿の問題であり、これらは学習という言葉を使えば意味がわかりやすい。例えば、$x$$i$と$y$$i$の生のデータをもとに、学習させたモデル(単回帰分析)で、学習させた範囲内の入力値$x$であれば予測値$\hat{y}$はそのモデルのとおり、十分に期待される予測値が出力される。一方で学習させた範囲外の$x$だった場合、そもそも学習されていない範囲での予測値$\hat{y}$となるので、全くもって期待されない予測値が出力されてしまう。これが内挿と外挿の関係である。
つまり内挿とは、訓練データの数値の範囲内で予測値を求めることを指し、外挿とは訓練データの数値の範囲外を入力値とすることであり、外挿では期待できない予測値が返ってくる。学生で例えるなら、ある学生が数学の試験で50〜100ページを勉強してきたのに対し、実際には150〜200ページの内容が試験として出題され、点数が取れないことに似ている。
ベクトルの定義
単回帰分析で用いるデータは基本的にベクトルとして持っておく必要がある。そのためにnumpyが必要となる。
#数値計算(ベクトルを定義するときなど)を行う場合は、numpyをインストールする
import numpy as np #数値計算用のライブラリ
x = np.array([[1, 2, 3]]) #2重に[]を書くのは、転置(行と列を入れ替える操作)の時に便利だから
y = np.array([[2, 3.9, 6.1]])
x
y
array([[1, 2, 3]])
array([[2. , 3.9, 6.1]])
データの中心化
データを取り扱う際、取り扱いが容易にするため、それらを中心化している。(後半にあるグラフをみてもらえれば中心化の意味が視覚でわかりやすい)
# データの取り扱いがしやすいようにするために、データを中心化することが一般的
x.mean() #各要素の平均値を算出
y.mean()
xc = x - x.mean() #各要素の値を、平均値から差し引くと、データを中心に移せる
yc = y - y.mean()
xc,yc
(array([[-1., 0., 1.]]), array([[-2. , -0.1, 2.1]]))
傾きaの計算
傾き$a$の計算は、次の数式で求めることができる。なお、$x$と$y$は中心化したデータを入力する必要がある。
$$ a = \frac{\sum_{n=1}^{N}x_{n}y_{n}}{\sum_{n=1}^{N}x_{n}^{2}} $$
xx = x * x
xy = x * y
a = xy.sum() / xx.sum()
a
2.007142857142857
Pandas
データを加工するために、使用するライブラリ。ここではcsvファイルを読み込み、それを表記したり、抽出したりしているだけ。
# Pandasはデータの加工を行うために使用するライブラリ
import pandas as pd
df = pd.read_csv('sample.csv')
df #データの中身全部
df.head(3) #先頭行のみ
df.tail(3) #最後の行のみ
df[:10] #行を抽出
df[10:]
df[10:16]
df.iloc[1, 1]
df['x'] #カラム名
df['y']
| 値 |
|---|
| 40.362 |
| 40.686 |
| 38.430 |
| 36.822 |
| 37.002 |
| ... |
| 47.250 |
| 43.722 |
| 42.642 |
| 43.644 |
| 41.850 |
Matplotlib
グラフを描画して可視化するために使用するライブラリ。
# Matplotlibはグラフを描画したりする際に使用するライブラリ
import matplotlib.pyplot as plt
x = df['x']
y = df['y']
#plt.scatter(x, y, c='blue')
fig = plt.figure(figsize=(10,10))
ax = fig.add_subplot(1, 1, 1)
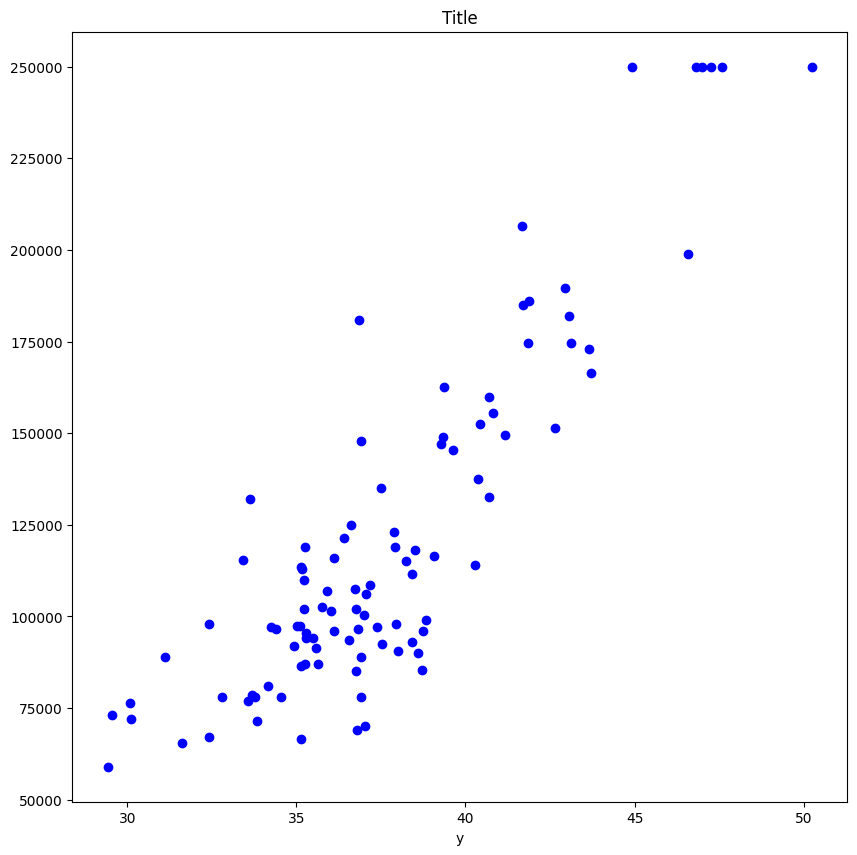
ax.scatter(x, y, c='blue')
ax.set_title('Title')
ax.set_xlabel('x')
ax.set_xlabel('y')
単回帰分析
基本的な単回帰分析は、以下の手順に従って、分析することができる。
ライブラリーの読み込みとファイルの読み込み
csvファイルに用意した大量の生データを、あらかじめ読み込ませておく。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
df = pd.read_csv('sample.csv')
df.describe()
| x | y | |
|---|---|---|
| count | 100.00000 | 100.00000 |
| mean | 37.62222 ・・・ (*) | 121065.0 ・・・ (*) |
| std | 4.08755 | 47174.01 |
| min | 29.41800 | 59000.0 |
| 25% | 35.15100 | 90375.0 |
| 50% | 36.90900 | 104250.0 |
| 75% | 39.43950 | 147250.0 |
| max | 50.25000 | 250000.0 |
※(*)は後半で用いる値。
データの中心化
読み込ませた大量のデータからを中心化しておく。
df_c = df - df.mean()
df_c
| x | y |
|---|---|
| 2.73978 | 16435.0 |
| 3.06378 | 11435.0 |
| 0.80778 | -28065.0 |
| -0.80022 | -24565.0 |
| -0.62022 | -20565.0 |
| ... | ... |
| 9.62778 | 128935.0 |
| 6.09978 | 45435.0 |
| 5.01978 | 30435.0 |
| 6.02178 | 51935.0 |
| 4.22778 | 53435.0 |
散布図の生成
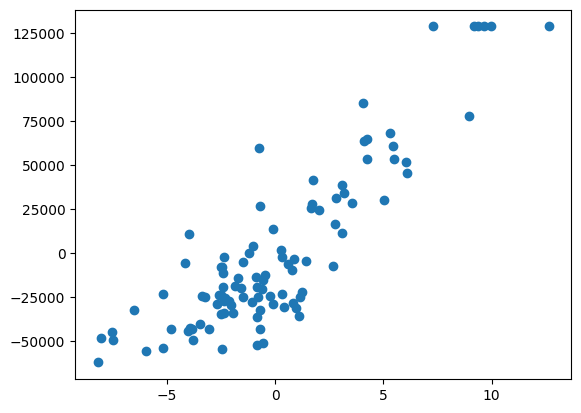
中心化したデータをグラフ化すれば、中心化されていることが容易に見てわかる。
x = df_c['x']
y = df_c['y']
plt.scatter(x,y);
傾きaの計算
読み込ませて、中心化させた大量のデータをもとに傾き$a$を求める
$$ a = \frac{\sum_{n=1}^{N}x_{n}y_{n}}{\sum_{n=1}^{N}x_{n}^{2}} $$
xx = x * x
xy = x * y
a = xy.sum() / xx.sum()
a
10069.022519284063 ・・・ (*)
※(*)は後半で用いる値。
傾きaをプロットに反映
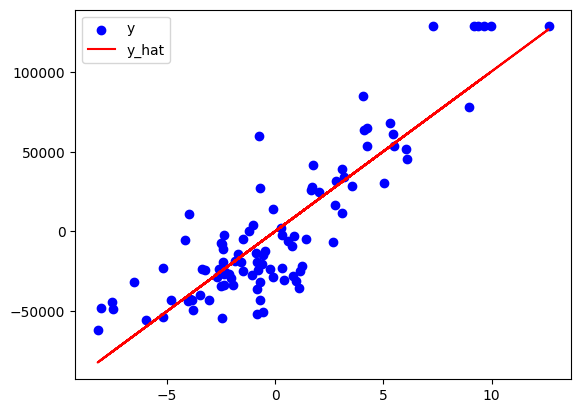
反映すると、各種データの中心側を沿っていることが見てわかる。(これが予測値を求める基本的な直線になるが、この後、中心化をもとに戻す作業が必要となる)
plt.scatter(x, y, c='blue', label='y')
plt.plot(x, a * x, c='red', label='y_hat')
plt.legend();
中心化前の情報に戻して、予測する
中心化前の情報に戻す手続きには、$x$$i$と$y$$i$の平均$\bar{x}$と$\bar{y}$が必要となる。(mean['x']やmean['y']の部分がその箇所)
x_new = 40 #ここでは仮に40として計算しているだけ
mean = df.mean()
mean['x'] #37.62222
xc_new = x_new - mean['x']
xc_new
yc = a * xc_new
yc
# 中心化前の状態に戻す
y_hat = yc + mean['y']
y_hat
リザルトを確認すれば、それらしい予測値が取得できる。
145006.92036590326
単回帰分析と重回帰分析の違い
単回帰分析では、予測したい値が一つの要素(変数)で決まる場合の際に使用する。一方で重回帰分析では、予測したい値が複数以上の要素(変数)で決まる場合の際に使用する。この記事でいうところの、$x$が$x$$1$,$x$$2$,$x$$3$...のように複数あるということ。つまり、予測したい現象や事象が複数の要因によって影響を受ける場合に、重回帰分析を用いる。