混合密度ネットワーク（Tensorflow2.0）

混合密度ネットワーク（Mixture Density Networks; MDN）を実装する必要があったので、チュートリアル？っぽいのを実装してみました。

参考
・Mixture Density Networks with TensorFlow
・Mixture Density Networks
・PRML第5章 混合密度ネットワーク Python実装 | Qiita

import

以下はimport済みとします。

import math
import random

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import tensorflow as tf
import tensorflow.keras as keras
from tensorflow.keras import layers as kl

1. 基本的なデータの予測

MDNを理解する上で、どういう性質のデータに適用できるかを順を追ってみていきます。
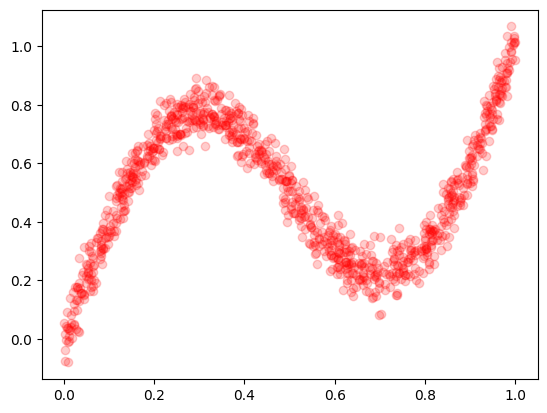
まずは以下のデータを予測します。

$y = 0.5 \sin(2 \pi x) + x + noise$

$noise$ はガウス分布に従う乱数です。(平均0、標準偏差0.05)
コードは以下です。

def create_dataset(data_num):
    x = np.random.uniform(0, 1, size=(data_num, 1)).astype(np.float32)
    noise = np.random.normal(loc=0, scale=0.05, size=(data_num,1))
    y = (0.5 * np.sin(2 * np.pi * x) + x + noise).astype(np.float32)
    return x, y

# データの可視化
x, y = create_dataset(1000)
plt.plot(x,y,'ro',alpha=0.2)
plt.show()

これを単純なニューラルネットに学習させてみます。
損失は平均二乗誤差（MSE）を使用します。

# モデル
model1 = keras.Sequential([
    kl.Input(shape=(1,)),
    kl.Dense(16, activation="relu"),
    kl.Dense(16, activation="relu"),
    kl.Dense(16, activation="relu"),
    kl.Dense(1),
])

# 学習
x_train, y_train = create_dataset(10000)
model1.compile(optimizer="adam", loss="mse")
history = model1.fit(x_train, y_train, batch_size=32, epochs=50)

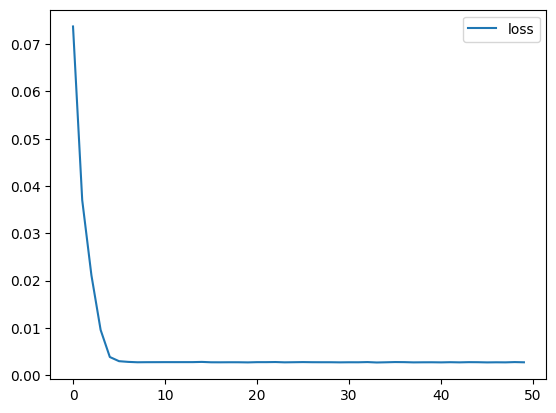
# 学習過程
df_hist = pd.DataFrame(history.history)
df_hist[["loss"]].plot()
plt.show()

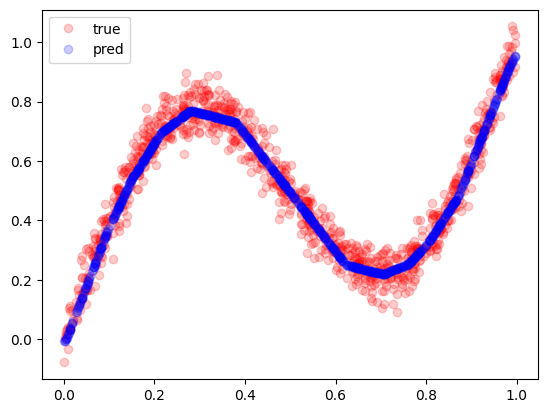
# 予測
x_true, y_true = create_dataset(1000)
y_pred = model1(x_true.reshape((-1, 1))).numpy()

plt.plot(x_true, y_true, 'ro', alpha=0.2, label="true")
plt.plot(x_true, y_pred, 'bo', alpha=0.2, label="pred")
plt.legend()
plt.show()

ちゃんと学習できていますね。

2. 答えが複数あるデータセットの予測

上記ですが、一般的に答えが1つになるデータしか予測できません。
（x,yの関係が1対1または多対1）

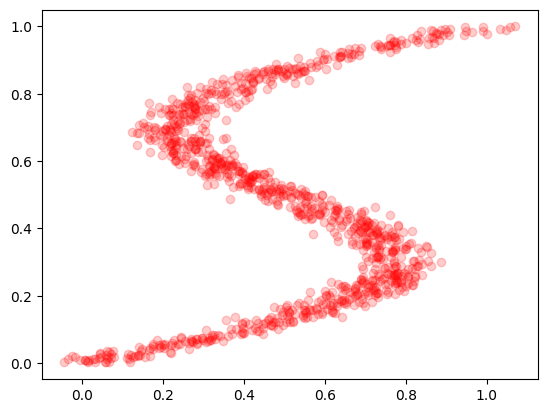
このデータセットのxとyを逆にしてみます。

def create_dataset2(data_num):
    x, y = create_dataset(data_num)
    return y, x

# データの可視化
x, y = create_dataset2(1000)
plt.plot(x, y, 'ro', alpha=0.2)
plt.show()

これは x に対して y が複数の値をとるのでこのままだと学習できません。
実際に学習させてみると以下になります。

# モデル
model2 = keras.Sequential([
    kl.Input(shape=(1,)),
    kl.Dense(16, activation="relu"),
    kl.Dense(16, activation="relu"),
    kl.Dense(16, activation="relu"),
    kl.Dense(1),
])

# 学習
x_train, y_train = create_dataset2(10000)
model2.compile(optimizer="adam", loss="mse")
model2.fit(x_train, y_train, batch_size=32, epochs=50)

# 予測
x_true, y_true = create_dataset2(1000)
y_pred = model2(x_true.reshape((-1, 1))).numpy()

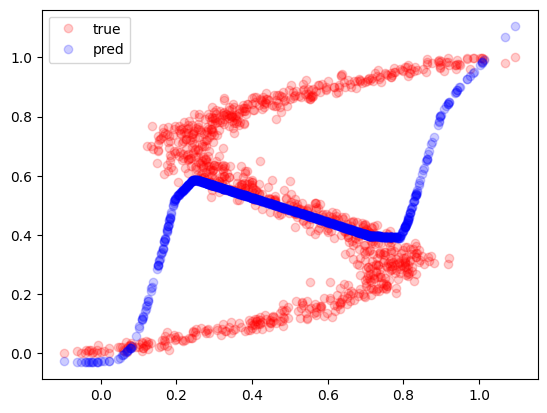
plt.plot(x_true, y_true, 'ro', alpha=0.2, label="true")
plt.plot(x_true, y_pred, 'bo', alpha=0.2, label="pred")
plt.legend()
plt.show()

学習できていませんね。

3. 混合密度ネットワークによる予測

上記ですが、値を直接予測するのではなく、混合ガウス分布と呼ばれる確率モデル（混合ガウスモデル、Gaussian Mixture Model; GMM）を予測します。
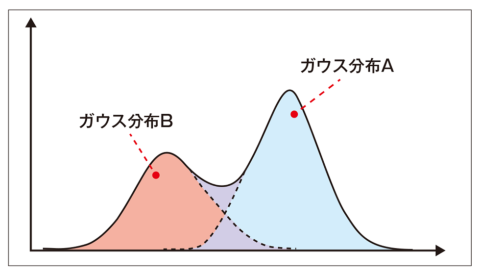
ガウス分布は1つの山を予測しますが、混合ガウス分布は複数の山を予測するイメージです。
（例えば3つの山なら、1つのxに対して3つのyの値を予測できるイメージ）

画像引用：https://xtrend.nikkei.com/atcl/contents/18/00076/00009/

MDNでは正規分布を $K$ 個の線形和として正規化します。
1個の正規分布は混合係数 $\pi(x)$、平均 $\mu(x)$、分散 $\sigma(x)$ の3つのパラメータを持ちます。（なので総パラメータ数は $3 \times K$）
xに対するyの条件付確率は以下です。

$$
P(y|x) = \sum_k{\pi_k(x) \phi(y | \mu_k(x), \sigma_k^2(x))}
$$

$\phi$ はガウス関数を表します。
また、混合係数 $\pi(x)$ ですが、合計すると1になる必要があります。（ $\sum_k{\pi_k(x)}=1$ ）
なので一般的にはソフトマックス関数を通すようです。

$$
\pi_k = \frac{\exp(\pi_k)}{\sum_i{\exp(\pi_i)}}
$$

これを学習するための損失関数は以下です。

$$
loss = - \log \sum_k{\pi_k(x) \phi(y,\mu_k(x), \sigma_k(x))}
$$

これで実装に必要な情報がそろったのでこのまま実装してもいいのですが、ニューラルネットから出力されるパラメータが対数の値と仮定すると計算が一部簡単になるので、ソフトマックス関数とガウス関数の対数も計算しておきます。

• ソフトマックス関数

$$
\log(\pi_k) = x_k - \log(\sum_{i=1}^N{\exp(x_i)})
$$

計算過程

\begin{align}
\log(\pi_k) &= \log(\exp(\pi_k)) - \log(\sum_i{\exp(\pi_i)}) \\
&= \pi_k - \log(\sum_i{\exp(\pi_i)})
\end{align}

• ガウス関数

$$
\log(\phi(y, \mu, \sigma)) =-\frac{1}{2} \Big( \log(2 \pi) + 2 \log(\sigma) + \frac{(y - \mu)^2}{ \sigma^2} \Big)
$$

計算過程

\begin{align}
\log(\phi(y, \mu, \sigma)) &= \log (\frac{1}{\sqrt{2 \pi \sigma^2 } }
\exp(- \frac{(y - \mu)^2}{ 2 \sigma^2} ) ) \\
&= \log (\frac{1}{\sqrt{2 \pi \sigma^2 } }) + \log(\exp(- \frac{(y - \mu)^2}{ 2 \sigma^2} ) )
\\
&= \log(1) - \log(\sqrt{2 \pi \sigma^2 }) - \frac{(y - \mu)^2}{ 2 \sigma^2}
\\
&= 0 - \log((2 \pi \sigma^2)^{ \frac{1}{2}}) - \frac{(y - \mu)^2}{ 2 \sigma^2}
\\
&= -\frac{1}{2} \log(2 \pi \sigma^2) - \frac{(y - \mu)^2}{ 2 \sigma^2}
\\
&= -\frac{1}{2} \Big( \log(2 \pi) + \log(\sigma^2) \Big) - \frac{(y - \mu)^2}{ 2 \sigma^2}
\\
&= -\frac{1}{2} \Big( \log(2 \pi) + 2 \log(\sigma) \Big) - \frac{(y - \mu)^2}{ 2 \sigma^2}
\\
&= -\frac{1}{2} \Big( \log(2 \pi) + 2 \log(\sigma) + \frac{(y - \mu)^2}{ \sigma^2} \Big)
\\
\end{align}

モデルと損失関数は以下です。

# 正規分布の数
num_mixture = 3

class MyModel(keras.Model):
    def __init__(self):
        super().__init__()
        
        in_l = c = kl.Input(shape=(1,))
        c = kl.Dense(32, activation="relu")(c)
        c = kl.Dense(32, activation="relu")(c)
        c = kl.Dense(32, activation="relu")(c)
        c3 = kl.Dense(num_mixture * 3)(c)
        self.model = keras.Model(in_l, c3)

    def call(self, x, training=False):
        return self.model(x)

def loss_function(y_true, y_pred):
    pi = y_pred[:, 0:num_mixture]
    mu = y_pred[:, num_mixture:num_mixture*2]
    log_sigma = y_pred[:, num_mixture*2:num_mixture*3]
    
    # ソフトマックス関数のオーバーフロー防止
    # (https://leico.github.io/TechnicalNote/Math/deep_learning)
    pi = pi - tf.reduce_max(pi, axis=1, keepdims=True)

    # log softmax
    log_pi = pi - tf.math.log(tf.reduce_sum(tf.exp(pi), axis = 1, keepdims = True))

    # los gauss
    log_gauss = -0.5 * (np.log(2 * np.pi) + 2 * log_sigma + (y_true - mu) ** 2 / tf.exp(log_sigma) ** 2)

    # loss
    loss = tf.reduce_sum(tf.exp(log_pi + log_gauss), axis=1, keepdims=True)
    loss = tf.maximum(loss, 1e-6)  # log(0) 回避
    loss = -tf.math.log(loss)
    return tf.reduce_mean(loss)

model3 = MyModel()
model3.compile(optimizer="adam", loss=loss_function)

パラメータの出力を1つにしてその後分割しているのは、Kerasのカスタム損失関数の引数が1つしか取れないからです。
参考：https://www.web-dev-qa-db-ja.com/ja/model/keras%E3%81%AE%E8%A4%87%E6%95%B0%E5%87%BA%E5%8A%9B%EF%BC%9A%E3%82%AB%E3%82%B9%E3%82%BF%E3%83%A0%E6%90%8D%E5%A4%B1%E9%96%A2%E6%95%B0/832423593/

学習コードです。

x_train, y_train = create_dataset2(10000)
history = model3.fit(x_train, y_train, batch_size=32, epochs=100, verbose=1)

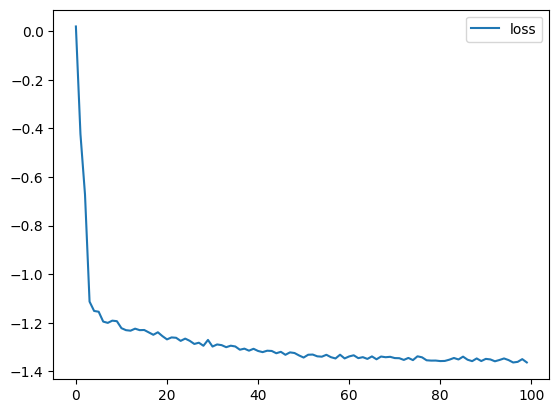
df_hist = pd.DataFrame(history.history)
df_hist[["loss"]].plot()
plt.show()

サンプリングのコードは以下です。
混合係数を元にした確率でガウス分布を選び、その後にサンプリングします。

def sample(model, x):
    x = model(x)
    pi = x[:, 0:num_mixture]
    mu = x[:, num_mixture:num_mixture*2]
    log_sigma = x[:, num_mixture*2:num_mixture*3]
    sigma = np.exp(log_sigma)

    # softmax
    exp_pi = tf.exp(pi - tf.reduce_max(pi, axis=1, keepdims=True))
    pi = exp_pi / tf.reduce_sum(exp_pi, axis=1, keepdims=True)

    samples = []
    for i in range(len(x)):
        
        # 混合係数の確率で選ぶ
        idx = random.choices([i for i in range(num_mixture)], weights=pi[i])

        # ガウス分布に従った乱数を出す
        z = np.random.normal(mu[i][idx], sigma[i][idx])
        samples.append(z)

    return samples


# --- 予測（サンプリング）
x_train, y_train = create_dataset2(1000)
y_pred = sample(model3, x_train)

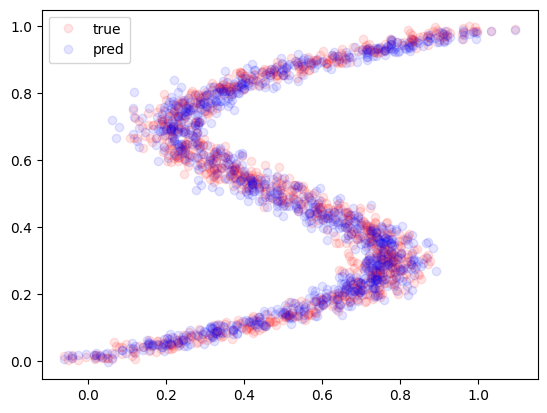
plt.plot(x_train, y_train, 'ro', alpha=0.1, label="true")
plt.plot(x_train, y_pred, 'bo', alpha=0.1, label="pred")
plt.legend()
plt.show()

ちゃんと予測できていますね。

おまけ、それぞれの確率分布の可視化

学習後の確率分布を可視化してみます。

• 平均

x_train, y_train = create_dataset2(500)
y_pred = model3(x_train)
mean = y_pred[:, num_mixture:num_mixture*2]

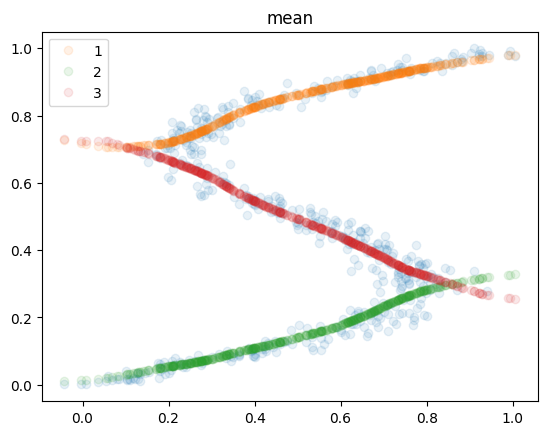
plt.plot(x_train, y_train, "o", alpha=0.1)
plt.plot(x_train, mean[:,0], 'C1o', alpha=0.1, label="1")
plt.plot(x_train, mean[:,1], 'C2o', alpha=0.1, label="2")
plt.plot(x_train, mean[:,2], 'C3o', alpha=0.1, label="3")
plt.legend()
plt.title("mean")
plt.show()

3個のガウス分布がちゃんとそれぞれの平均を学習していますね。

• 分散

x = np.linspace(0, 1, 100)
y = model3(x)
log_sigma = y[:, num_mixture*2:num_mixture*3]
sigma = np.exp(log_sigma)

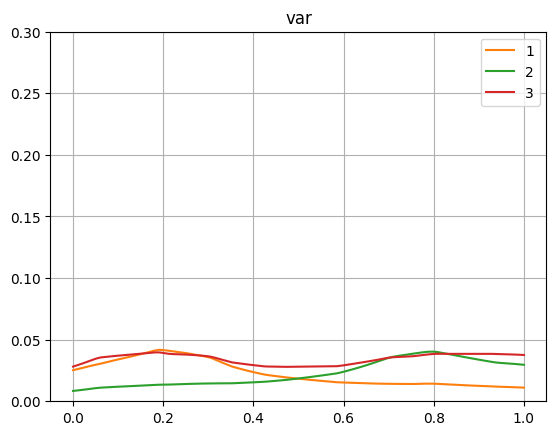
plt.plot(x, sigma[:,0], "C1", label="1")
plt.plot(x, sigma[:,1], "C2", label="2")
plt.plot(x, sigma[:,2], "C3", label="3")
plt.ylim(0, 0.3)
plt.legend()
plt.title("var")
plt.grid()
plt.show()

今回はノイズとして0.05の分散の値を入れています。
どの確率分布も近い値で学習されていますね。

• 混合係数

x_train, y_train = create_dataset2(500)

x = np.linspace(0, 1, 100)
y = model3(x)
pi = y[:, 0:num_mixture]
pi = np.exp(pi) / np.sum(np.exp(pi), axis=1, keepdims=True)

fig = plt.figure()
ax1 = fig.add_subplot(111)
ax2 = ax1.twinx()

# 1軸
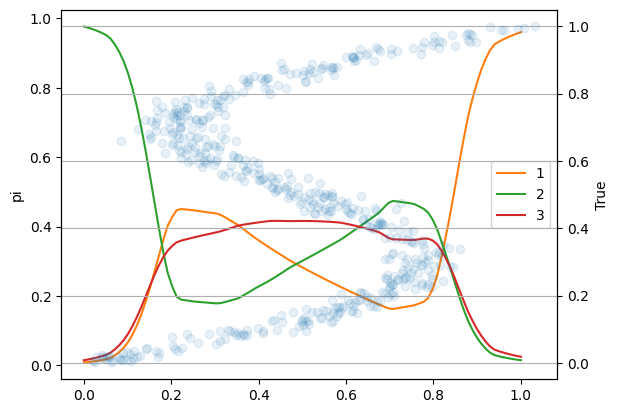
ax1.plot(x, pi[:,0], "C1", label="1")
ax1.plot(x, pi[:,1], "C2", label="2")
ax1.plot(x, pi[:,2], "C3", label="3")
ax1.set_ylabel("pi")
ax1.legend()

# 2軸
ax2.plot(x_train, y_train, "o", alpha=0.1)
ax2.set_ylabel("True")

plt.grid()
plt.show()

混合係数は、各分布の反映率みたいなものです。
平均と見比べてもらえればと思いますが、左下は2番の分布がメインなので2番の混合係数が大きいです。
真ん中は3個の分布が割と均等にあるのでどれも似た値ですね。
右上は1番の分布がメインなので1番の混合係数が大きくなっています。

おわりに

以前に TensorFlow Probability を用いた混合ガウス分布の予測は記事に書いていますが、必要があったのでライブラリを使わずに実装しました。