この記事は自作している強化学習フレームワークの解説記事です。
以前書いた記事とほとんど同じ内容ですが、フレームワーク用に改めて書きました。
以前の記事:第6回 今更だけど基礎から強化学習を勉強する PPO編
PPO(Proximal Policy Optimization)
方策を直接学習するアルゴリズムとして方策勾配法がありました。(方策勾配法についてはこちらの記事を参照)
方策勾配法は方策の更新として方向のみしか教えてくれず、更新幅が分からないという問題がありました。
方策の大幅な変更は方策が劣化する可能性があります。
方策が劣化すると報酬の少ないサンプルのみを収集し、更に方策が劣化するという悪循環に陥る可能性があります。
そこで、TRPO(Trust Region Policy Optimization)では方策の大幅な変更を回避するために、更新幅に制約を設けて学習する手法を提案しました。
TRPOはとても優れたアルゴリズムでしたが、計算がとても複雑という欠点がありました。
また、他にも以下の課題がありました。
- ノイズ(Dropout層など)を組み込めない
- ActorとCriticでパラメータを共有するアーキテクチャが使えない
これらの課題を解決するためにTRPOとは違ったアプローチで更新幅を制限した手法がPPOとなります。
また、PPOはA3Cも参考にしているので分散学習の話もありますが、本質ではないのでこの記事では省略しています。
参考
・論文:https://arxiv.org/abs/1707.06347
・ハムスターでもわかるProximal Policy Optimization (PPO)①基本編
・Proximal Policy Optimization(OpenAI)
・baselines/ppo2(github)
Clipped Surrogate Objective
TRPOでは以下の式(代理目的関数:Surrogate Objective)を最大化しつつ、KL距離による制約をかけて更新幅を抑える手法を提案しました。
$$
\underset{\theta}{\text{maximize}} L(\theta) = \hat{E}[ \frac{\pi_{\theta} (a|s)}{ \pi_{\theta_{old}}(a|s)} \hat{A} ]
$$
ただ、この式をKL距離の制約の元で解こうとするととても複雑になります。(ラグランジュ乗数法で解くとの事)
そこでPPOでは制約条件の代わりに単純にclipすることで更新幅を抑える事を提案しました。
clipの方法は以下となります。
まず、代理目的関数内の更新前の方策 $\pi_{\theta} (a|s)$ と更新後の方策 $\pi_{\theta_{old}}(a|s)$ の比を $r_t(\theta)$ と置きます。
$$
r_t(\theta) = \frac{\pi_{\theta} (a|s)}{ \pi_{\theta_{old}}(a|s)}
$$
そしてclip条件は以下です。
$$
L^{CLIP}(\theta) = \hat{E}[ min(r(\theta) \hat{A}, clip(r(\theta), 1 - e, 1+e) \hat{A})]
$$
$e$ はclip範囲を決めるハイパーパラメータです。
clipしてない代理目的関数とclipされた代理目的関数を比較し小さい方を採用します。
数式だと分かりづらいですが、コードだと以下です。
old_pi = 更新前の方策(確率)
new_pi = 更新後の方策(確率)
advantage = 計算した割引報酬率(にbaseline等加味したもの)
epsilon = 0.2 # clip範囲
ratio = new_pi / old_pi
ratio_clipped = tf.clip_by_value(ratio, 1 - epsilon, 1 + epsilon)
loss_unclipped = ratio * advantage
loss_clipped = ratio_clipped * advantage
# 小さい方
loss = tf.minimum(loss_unclipped, loss_clipped)
Adaptive KLペナルティ
TRPOの制約条件に関する別のアプローチとして、目的関数に直接KL距離のペナルティを組み込む手法も提案されています。
ただ、あまり性能向上に貢献できていないようです。
L^{KLPEN}(\theta) = \hat{E}
\begin{bmatrix}
\frac{\pi_{\theta} (a|s)}{ \pi_{\theta_{old}}(a|s)} \hat{A}
- \beta KL[\pi_{\theta_{old}} ( . |s) || \pi_{\theta} (.|s)]
\end{bmatrix}
$\beta$ はハイパーパラメータですが、以下の式で自動調整されます。
\begin{align}
d = \hat{E}
\begin{bmatrix}
KL[\pi_{\theta_{old}} ( . |s) || \pi_{\theta} (.|s)]
\end{bmatrix}
\\
\beta = \left\{
\begin{array}{ll}
\frac{\beta}{2} & (d < \frac{d_{targ}}{1.5})\\
2 \beta & (d > 1.5 d_{targ})\\
\beta & (otherwise)
\end{array}
\right.
\end{align}
$d_{targ}$ は定数(0.01等)です。
コード例は以下となります。
# KL距離の計算(離散ver、softmax)
def compute_kl_divergence(prob1, prob2):
return tf.reduce_sum(prob1 * tf.math.log(prob1 / prob2), axis=1, keepdims=True)
# KL距離の計算(連続ver、ガウス分布)
def compute_kl_divergence_normal(mean1, stddev1, mean2, stddev2):
a1 = tf.math.log(stddev2 / stddev1)
a2 = (tf.square(stddev1) + tf.square(mean1 - mean2)) / (2.0 * tf.square(stddev2))
a3 = -0.5
return a1 + a2 + a3
adaptive_kl_target = 0.01
adaptive_kl_beta = 0.5
# 学習のタイミング
def train():
states = 状態
old_probs = 経験取得時の各アクションの確率
# 勾配計算
with tf.GradientTape() as tape:
new_probs = 現在のモデルから出したアクション確率
policy_loss = 計算した後の方策loss
# KLペナルティ
kl = compute_kl_discrete(old_probs, new_probs)
policy_loss -= adaptive_kl_beta * kl
(略)
# ミニバッチ
loss = tf.reduce_mean(loss)
# KLペナルティβの調整
kl_mean = tf.reduce_mean(kl)
if kl_mean < adaptive_kl_target / 1.5:
adaptive_kl_beta /= 2
elif kl_mean > adaptive_kl_target * 1.5:
adaptive_kl_beta *= 2
各手法の比較
折角なので前記事では省いた内容を追加しておきます。
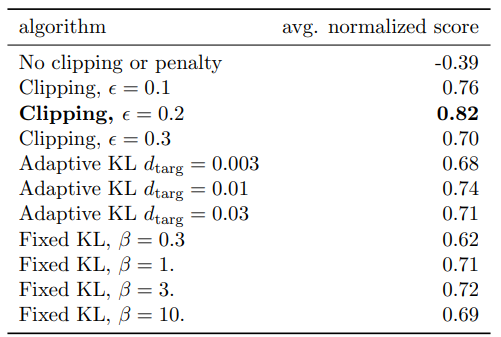
論文内で提案されている手法について比較しているのでそれを見てみます。
比較手法は以下の3つ+ハイパーパラメータです。
No clipping or penalty(補正なし) : $L(\theta) = r_t(\theta)\hat{A_t}$
Clipping(提案手法) : $L(\theta) = r_t(\theta)\hat{A_t}$
KL penalty(KLペナルティによる補正) : $L(\theta) = r_t(\theta)\hat{A_t} - \beta KL[\pi_{\theta_{old}} ( . |s) || \pi_{\theta} (.|s)]$
KL penaltyは更に2種類あり、Adaptiveは$\beta$を自動的に調整、Fixedは$\beta$を固定にします。
比較にはOpenAI GymのMuJuCoから7種類の環境を21回実行し、その平均正規化をスコアとして比較しています。(正規化は多分環境によって報酬の範囲がバラバラだから)
clipしない場合は学習ができていませんね。(スコアがマイナス)
一番スコアが良かったのがclipする場合で $\epsilon=0.2$ の場合だとの事です。
Advantage(GAE)の計算
価値の推定ですが、PPOではGAEが採用されています。
GAE(Generalized Advantage Estimator)では未来の価値をTD誤差を元に推定する方法となります。
TD誤差 $\delta_t^V$ は以下です。
$$ \delta_t^V = r_t + \gamma V(s_{t+1}) - V(s_t)$$
これを元にTD(λ)法のように各ステップをλで重みづけした手法がGAEとなります。
\hat{A}_t^{GAE(\gamma, \lambda)} = (1 - \lambda)(\delta_t^V + \lambda (\delta_t^V + \gamma \delta_{t+1}^V) + \lambda^2 (\delta_t^V + \gamma \delta_{t+1}^V + \gamma^2 \delta_{t+2}^V) + ... )
この式を解くと以下になります。
\hat{A}_t^{GAE(\gamma, \lambda)} = \sum^{\infty}_{l=0}( \gamma \lambda)^l \delta^V_{t+l}
コード例は以下です。(MC法も比較用に書いています)
# --- GAE
class Worker(RLWorker):
# エピソードの最初に呼ばれる
def call_on_reset(self, worker: WorkerRun) -> dict:
self.recent_states = []
self.recent_next_states = []
self.recent_rewards = []
self.recent_batch = [] # バッチ用のデータを格納する
return {}
# action決定するタイミングで呼ばれる
def call_policy(self, worker: WorkerRun) -> Tuple[Any, dict]:
self.state = worker.state # env.step前の状態を保存しておく
action = モデルからアクションを決定
self.batch = 学習に必要な情報(アクションの確率等)
return action, {}
# env.step後に呼ばれる
def call_on_step(self, worker: WorkerRun) -> dict:
reward = worker.reward
done = worker.done
# 各stepの情報を保存する
self.recent_states.append(self.state)
self.recent_next_states.append(worker.state)
self.recent_rewards.append(reward)
self.recent_batch.append(self.batch)
if done:
# 状態価値を推定
# (vは学習直後に計算したほうがより良いが、MCとの比較のためエピソード最後としている)
# (学習時にGAEを計算する場合、エピソード全体のstateをbatchにするのでメモリサイズは大きくなる)
v = self.parameter.model.value(np.array(self.recent_states))
n_v = self.parameter.model.value(np.array(self.recent_next_states))
v = v.numpy().reshape((-1,))
n_v = n_v.numpy().reshape((-1,))
# エピソード最後から計算する
gae = 0
for i in reversed(range(len(self.recent_rewards))):
r = self.recent_rewards[i]
if i == len(self.recent_rewards) - 1:
# エピソード最後は次の状態価値はない
delta = r - v[i]
else:
# delta = r + γV(t+1) - V(t)
delta = self.recent_rewards[i] + self.config.discount * n_v[i] - v[i]
# A = delta(t) + γ*λ*delta(t+1)
gae = delta + self.config.discount * self.config.gae_discount * gae
# 各stepのGAEを保存し、バッチとする
batch = self.recent_batch[i]
batch["discounted_reward"] = gae
self.remote_memory.add(batch)
return {}
# --- MC
class Worker(RLWorker):
# エピソードの最初に呼ばれる
def call_on_reset(self, worker: WorkerRun) -> dict:
self.recent_rewards = []
self.recent_batch = [] # バッチ用のデータを格納する
return {}
# action決定するタイミングで呼ばれる
def call_policy(self, worker: WorkerRun) -> Tuple[Any, dict]:
action = モデルからアクションを決定
self.batch = 学習に必要な情報(アクションの確率等)
return action, {}
# env.step後に呼ばれる
def call_on_step(self, worker: WorkerRun) -> dict:
reward = worker.reward
done = worker.done
# 各stepの情報を保存する
self.recent_rewards.append(reward)
self.recent_batch.append(self.batch)
if done:
# エピソード最後から計算する
mc_r = 0
for i in reversed(range(len(self.recent_rewards))):
r = self.recent_rewards[i]
mc_r = r + self.config.discount * mc_r
# 各stepの割引報酬を保存し、バッチとする
batch = self.recent_batch[i]
batch["discounted_reward"] = r
self.remote_memory.add(batch)
return {}
参考
- High-Dimensional Continuous Control Using Generalized Advantage Estimation(論文)
- Notes on the Generalized Advantage Estimation Paper
- 一般化報酬による高次元の強化学習の論文を読む
- OpenAIのSpinning Upで強化学習を勉強してみた その4
その他のテクニック
以下の論文を参考に、細かいテクニックも見てみます。
Implementation Matters in Deep Policy Gradients: A Case Study on PPO and TRPO(論文)
1. Value Clipping
Clipped Surrogate Objective は方策モデルに対して行っていますが、これを価値関数にも行う方法です。
$\epsilon$ は Clipped Surrogate Objective と同じ値を使用するとの事。
また、数式上は $t-1$ になっていますが、ここの $t$ は step のことではなさそうで、$V_{\theta_{t-1}}$ は以前の推定値との記載がありました。
$$
L^V = \max[
(V_{\theta_{t}} - V_{targ})^2 ,
(clip(V_{\theta_{t}}, V_{\theta_{t-1}} - \epsilon, V_{\theta_{t-1}} + \epsilon) - V_{targ})^2
]
$$
old_v = 経験収集時の状態価値
advantage = 計算した割引報酬率(にbaseline等加味したもの)
pi_clip_range = 0.2 # クリップ幅
# 勾配計算箇所
with tf.GradientTape() as tape:
# 現在の状態価値
v = model(states)
(略)
#--- Value loss
v_clipped = tf.clip_by_value(v, old_v - pi_clip_range, old_v + pi_clip_range)
value_loss = tf.maximum((v - advantage) ** 2, (v_clipped - advantage) ** 2)
2. Reward scaling
割引報酬和のスケーリング(baseline)ですが、標準偏差で割る手法です(平均は引きません)
報酬がスパース(報酬がなかなか取得できない場合)は逆に不安定になるようです。
コードはnoneも含め5種類作成しておきました。
advantage = 割引報酬
baseline_type = "std"
if baseline_type == "none":
pass
elif baseline_type == "ave":
advantage -= np.mean(advantage)
elif baseline_type == "std":
advantage = advantage / (np.std(advantage) + 1e-8)
elif baseline_type == "normal":
advantage = (advantage - np.mean(advantage)) / (np.std(advantage) + 1e-8)
elif self.config.baseline_type == "advantage":
v = model(states)
advantage -= v
3. Orthogonal initialization and layer scaling
方策・価値モデルの重みの初期化ですが、レイヤー毎にバラバラになるように直交行列で初期化したほうがパフォーマンスが向上するようです。
Kerasではレイヤーの kernel_initializer 引数をOrthogonalにする事で実現できます。
init_layer_weight = "orthogonal"
# kernel_initializer 省略時の初期値
if init_layer_weight == "":
init_layer_weight = "glorot_uniform"
nb_actions = アクション数
dense_units = ユニット数
activation = "tanh"
# 各レイヤーの定義
dense1 = keras.layers.Dense(dense_units, activation=activation, kernel_initializer=init_layer_weight)
dense2 = keras.layers.Dense(dense_units, activation=activation, kernel_initializer=init_layer_weight)
actor_layer = keras.layers.Dense(nb_actions, kernel_initializer=init_layer_weight)
critic_layer = keras.layers.Dense(1, kernel_initializer=init_layer_weight)
4. Adam learning rate annealing
Adamの学習率ですが、徐々に下げていく(焼きなまし法)ほうがパフォーマンスが向上するようです。
Kerasでは optimizer の学習率 lr は直接変更できます。
optimizer_initial_lr = 0.02 # 初期学習率
optimizer_final_lr = 0.01 # 終了学習率
optimizer_lr_step = 200*50 # 終了学習率になるまでの更新回数
model.optimizer = Adam()
update_count = 0
# 1回学習毎
def update():
if update_count > optimizer_lr_step:
model.optimizer.lr = optimizer_final_lr
else:
model.optimizer.lr = optimizer_initial_lr - \
(optimizer_initial_lr - optimizer_final_lr) * \
(update_count / optimizer_lr_step)
update_count += 1
5. Reward Clipping
報酬は事前設定された範囲([-5,5]または[-10,10]など)でclipします。
reward_clip = [-5, 5] # clip範囲
# 1stepのタイミング
n_state, reward, done, _ = env.step(action)
# 報酬のclip
if reward_clip is not None:
reward = np.clip(reward, reward_clip[0], reward_clip[1])
6. Observation Normalization
状態を標準化(平均0、分散1に正規化)して学習に使います。
# 学習時
states = 状態
# 状態を正規化
states = (states - np.mean(states, axis=0, keepdims=True)) / \
(np.std(states, axis=0, keepdims=True) + 1e-8)
7. Observation Clipping
報酬と同様に状態もclipします。(通常は[-10,10])
state_clip = [-10, 10] # clip範囲
# 1stepのタイミング
n_state, reward, done, _ = env.step(action)
# 状態のclip
if state_clip is not None:
state = np.clip(state, state_clip[0], state_clip[1])
8. Hyperbolic tan activations
方策/価値モデルの活性化関数は Hyperbolic tan(tanh) が使われるようです。
コードは 3. に記載してあります。
9. Global Gradient Clipping
方策/価値モデルの勾配を計算した後、全てのパラメータはL2(ノルム2)でclipします。
global_gradient_clip_norm = 0.5 # clip範囲
with tf.GradientTape() as tape:
(省略)
loss = tf.reduce_mean(loss)
grads = tape.gradient(loss, model.trainable_variables)
# L2でクリップ
grads, _ = tf.clip_by_global_norm(grads, global_gradient_clip_norm)
model.optimizer.apply_gradients(zip(grads, model.trainable_variables))
(おまけ)アクションの(逆?)正規化
論文には書いていないですが実装上のテクニックとして書いておきます。
連続行動空間に限った話ですが、アクションの範囲を制限して学習します。
学習では[-1,1]の範囲で学習し、環境へは適切な範囲に置き換えて渡します。
例えば環境の取りうる値が[0,10]の場合は $5a + 5$ して渡します。
action_center = (action_space.high + action_space.low)/2
action_scale = action_space.high - action_center
action = アクション
env_action = action * action_scale + action_center
# 1step
env.step(env_action)
サンプルコード
実装コードおよびサンプルコードはgithubを見てください。