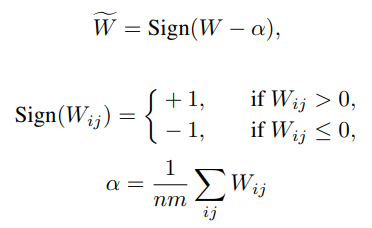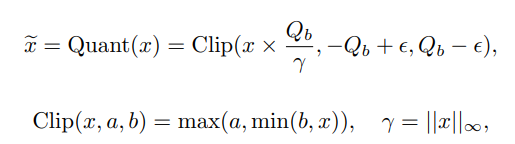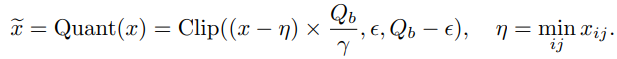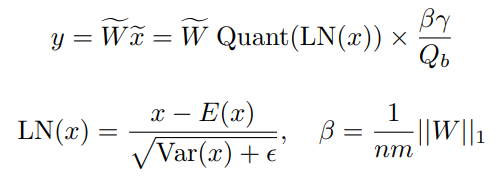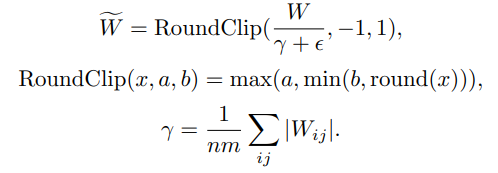LoginSignup
15
8
@pocokhc(ちぃがぅ)

BitNet b1.58(BitLinear)を実装してMNISTで検証してみた(Tensorflow/Torch)

Last updated at Posted at 2024-03-15

はじめに

2/27にMicrosoftから BitNet b1.58 に関する論文が発表されました。
これはモデルの推論を従来の小数でするのではなく、ビットで推論する事により速度・メモリを含めたエネルギーの省力化を実現した内容となります。
（ディープラーニングにおいて、こういったモデルを低ビット等に離散化して計算量を減らす技術のことを量子化といいます）
（ちなみに私は量子化分野はほとんど分からないので間違っている内容があればすいません…）

論文では主にTransformerの利用に言及していますが、仕組み自体は単純でニューラルネット全般に適用できるので、そちらの視点をメインに書いています。
また、BitNetに関する解説記事はすでに分かりやすい記事があるので、この記事では技術メインに解説していきます。

・【論文丁寧解説】BitNet b1.58とは一体何者なのか

また実装に関してですが、多分まだ公式のコードはないようなので論文ベースで実装していきます。
Github上にはいくつかコードがあるのですが、論文と違っていたりまだ作成途中だったりしていい感じのがなかったので自作しました。
参考文献は以下です。

・（論文1）BitNet: Scaling 1-bit Transformers for Large Language Models
・（論文2）The Era of 1-bit LLMs: All Large Language Models are in 1.58 Bits
・https://github.com/kyegomez/BitNet （非公式？b1.58に関しては作成中っぽい）
・BitNet&BitNet b158の実装
・BitNetから始める量子化入門
・【BitNet b1.58】1ビットでLLaMAよりも性能が優れているLLMを使ってみた

本記事のコードは以下です。

BitLinear（BitNet）

技術だけを見ると論文1がメインで論文2はちょっとした変更みたいな感じなので、まずは論文1のBitLinearを見ていきます。
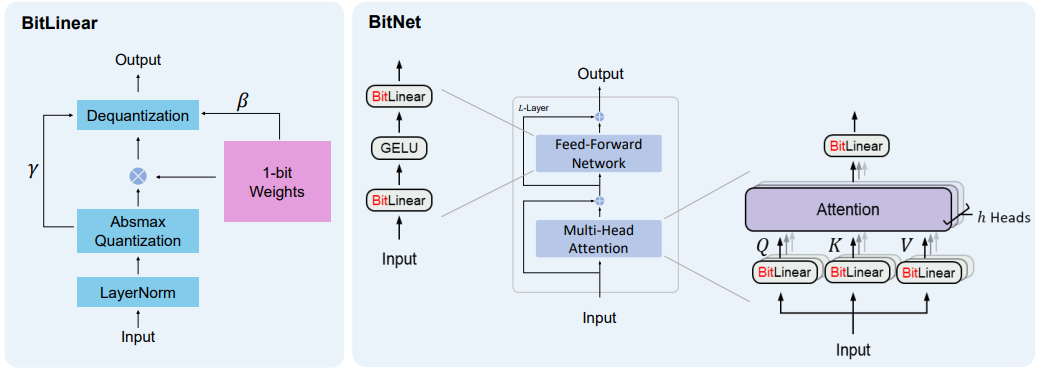
BitLinearの概要は以下です。（論文より）

ss1.png

左側がBitLinearでLinear層（torchならnn.Linear、tfならDense）の置換を想定しています。
右側がLinear層をBitLinear層に置き換えたTransformerになります。
本記事では右側のBitNetには触れません。
興味があるのがあくまでBitLinearだけだったので…。

BitLinearには大きく4つの処理があるのでそれぞれを解説していきます。

0. Linear層の概要

解説に入る前にLinear層の説明をしておきます。
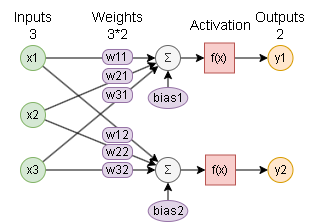
ニューラルネットワークのニューロン（計算ノード）のイメージは以下です。（入力3、出力2の例）

aa-ページ3.drawio.png

$y1$ の計算は以下となります。

\begin{align}
x1' &= (w11 \times x1 + w21 \times x2 + w31 \times x3) + bias1 \\
y1 &= f(x1') \\
\end{align}

$f$ は活性化関数でニューロンの性質を決める関数です。
Linear層は活性化関数が線形 $f(x) = x$ の場合となり、いわゆる値をそのまま出力するニューロンの事を言います。

1. Weightsの量子化（1-bit Weights）

重みを{-1,1}の2値化で量子化します。
（2種類なので1bit）
（図で言うところの w11,w21,w31,w12,w22,w32 の箇所を量子化します）

数式は以下です。

ss2.png

$W$が量子化前の重みで$\tilde{W}$が量子化後の重みで、$\alpha$ は重みの平均です。
$Sign$ 関数が少し特殊で、普通は0の時には0を返しますが、-1を返すようです。

コードは以下です。
self.weightがニューラルネットの重みを表しています。

Tensorflow
# Tensorflow
alpha = tf.reduce_mean(self.weight)
weight = self.ste_sign(self.weight - alpha)
Torch
# Torch
alpha = self.weight.mean()
weight = self.ste_sign(self.weight - alpha)

※ self.ste_sign については後述しますが、符号を返す sign 関数と同じ動作をします

biasについて

ちなみにbiasについては論文1では特に触れられていません。
論文2ではすべて削除しているとの事ですので、実装ではデフォルトは使用しない方向で使用する場合は特に何もしていません。

2. 入力値の量子化（Absmax Quantization）

入力を8-bitに量子化します。（図で言うところの x1,x2,x3 の箇所）
8bitなので量子化後の値の範囲は[-127,127]になります。

数式は以下です。

ss3.png

$x$が入力値で$\tilde{x}$が量子化後の入力値、$Q_b$は $Q_b=2^{b-1}$、$b=8$の定数です。
$\gamma=||x||_{\infty}$ は$L{\infty}$ノルムの事で、絶対値の最大値となります。

計算としては、$x$を最大値で割ることで、$\frac{x}{\gamma}$は$[-1,1]$の範囲になり、これに$Q_b$を掛けることで$[-Qb,Qb]$の範囲にしています。
最後に、$\frac{x}{\gamma}Q_b$に対して $[-Q_b+\epsilon, Q_b-\epsilon]$ になるように$Clip$します。
$\epsilon$は$Clip$時のオーバーフローを防ぐ小さな定数です。
（参考記事にありましたが、確かにclipの意味がないような？）

コードは以下です。
xが入力値を表しています。

# 定数
bits = 8
Qb = 2 ** (bits - 1)
eps = 1e-5
Tensorflow
gamma = tf.reduce_max(tf.abs(x))
x = x * Qb / gamma
x = tf.clip_by_value(x, -Qb + eps, Qb - eps)
Torch
gamma = torch.abs(x).max()
x = x * Qb / gamma
x = torch.clamp(x, - Qb + eps, Qb - eps)

コード上は小数のままで特に整数の処理は入れていません。
値がほぼ整数の近似値になるので整数処理を入れても性能に変化はないと思われます。
ちゃんとbit演算で高速化するなら整数への変換が必要になりそうです。

活性化関数が非線形関数の場合のスケール

論文1ではBitLinear層の後の活性化関数がReLU等の非線形関数の場合、スケール範囲を$[0, Q_b]$ にするとの事です。
これは論文2では廃止されている処理となります。

数式とコードは以下です。

ss4.png

Tensorflow
eta = tf.reduce_min(x)
x = (x - eta) * Qb / gamma
x = tf.clip_by_value(x, eps, Qb - eps)
Torch
eta = torch.min(x)
x = (x - eta) * Qb / gamma
x = torch.clamp(x, eps, self.Qb - eps)

3. 行列の計算

量子化したxとwを加算します。（図でいうΣの箇所です）
量子化前の計算は以下でした。（biasは省略）

$$
x1' = w11 \times x1 + w21 \times x2 + w31 \times x3
$$

ここで量子化後はwが{-1,1}または{-1,0,1}の値しかない状態になります。（3値化に関しては後述）
例えば w11=-1, w21=1, w31=0 とします。

\begin{align}
x1' &= -1 \times x1 + 1 \times x2 + 0 \times x3 \\
&= -x1 + x2 \\
\end{align}

乗算がなくなり加算だけで計算できるようになりました。
さらにxも量子化されて8bitなのでbit演算で処理できるようになっています。
これは乗算が得意なGPUより、このシンプルな計算に特化したハードウェアを使った方が計算が早そうです。
これでさらなる高速化ができるよねというのが論文の主張です。

ただ、実装ではこの高速な計算は実現できないので、今までと同じ処理で実装します。

Tensorflow
x = tf.matmul(x, weight)
if self.use_bias:
    x = tf.nn.bias_add(x, self.bias)
Torch
x = torch.nn.functional.linear(x, weight, self.bias)

4. 入力の正規化

ここの論文の言い回しが理解できている自信がありません…。
ちゃんと理解したい人は論文を読んでみてください。

Linear層を通した後の出力ですが、よくある初期化方法だと1が想定されます。（Kaiming initialization や Xavier initialization 等）
量子化後も分散を保持するために量子化前に分散が1になるように正規化を導入します。
量子化前に分散を1にしておくことで、BitLinearの出力も分散が保持されるとの事です。

正規化方法はLayerNormalizationを使用します。

5. 出力値の逆量子化（Dequantization）

最後に量子化されている値を元に戻します。
数式は以下です。

ss5.png

$LN(x)$ は LayerNormalization、$\tilde{W}$は量子化後の重み、$Quant(LN(x))$は量子化後の入力値を表します。
$\frac{\beta \gamma}{Q_b}$ が逆量子化用の再スケール値で、$\gamma$ は「2. 入力値の量子化」で計算した$\gamma$と同じもので、$\beta$ はL1ノルムの平均値です。

コードは以下です。

Tensorflow
beta = tf.reduce_mean(tf.abs(self.weight))
x = x * gamma * beta / Qb
Torch
beta = torch.abs(self.weight).mean()
x = x * gamma * beta / Qb

BitLinear 1.58bit

BitLinearは以上で残りは論文2の内容です。
変更箇所としては2つです。

  • 重みの量子化を {-1, 1} から {-1, 0, 1} に変更
  • 活性化関数が非線形関数の場合のスケールを廃止

重みの値が3つの場合の情報エントロピーを計算すると

$$
H = -3\times\frac{1}{3}log_2(\frac{1}{3}) = log_2(3) \approx 1.58496250072 (bit)
$$

なので1.58bitと表現されています。

3値化の方法ですが、絶対平均で量子化します。(absmean quantization function)
数式は以下です。

ss6.png

$\gamma$ですが、論文が違うので$\gamma$表記ですが論文1の$\beta$と同じものです。
コードは以下です。

Tensorflow
gamma = beta
weight = self.weight / (gamma + eps)
weight = self.ste_round(weight)
weight = tf.clip_by_value(weight, -1, 1)
Torch
gamma = beta
weight = self.weight / (gamma + eps)
weight = self.ste_round(weight)
weight = torch.clamp(weight, -1, 1)

※ self.ste_round については後述しますが、四捨五入する round 関数と同じ動作をします

Straight-through estimator

実装で一番苦労した点…。
学習時の逆伝搬ですが、sign関数やclip関数が微分不可能なので勾配が流れません。
これをStraight-through estimator(STE)という方法で勾配を流します。1

STEは順伝搬は普通に計算しますが、逆伝搬ではそのまま値を返すように実装する方法です。
コード例は以下です。

Tensorflow
def ste_f(self, x):
    x2 = 微分できない何かしらの計算
    return tf.stop_gradient(x2 - x) + x

# これでも同じらしい
@tf.custom_gradient
def ste_f(self, x):
    def grad(dy):
        return dy
    x = 微分できない何かしらの計算
    return x, grad
Torch
def ste_f(self, x):
    x2 = 微分できない何かしらの計算
    return (x2 - x).detach() + x

順伝搬では (x2-x)+x == x2 となり計算結果の x2 が返ります。
逆伝搬では (x2-x) が無視され、x のみが返ります。

問題だったのは勾配が流れない関数が何か分からない事でした…
多分sign関数とclip関数だけだと思います。
実装コードは以下。

Tensorflow
def ste_sign(self, x):
    x2 = tf.cast(tf.where(x > 0, 1, -1), x.dtype)
    return tf.stop_gradient(x2 - x) + x  # STE

def ste_round(self, x):
    x2 = tf.round(x)
    return tf.stop_gradient(x2 - x) + x  # STE
Torch
def ste_sign(self, x):
    x2 = torch.where(x > 0, 1, -1)
    return (x2 - x).detach() + x  # STE

def ste_round(self, x):
    x2 = torch.round(x)
    return (x2 - x).detach() + x  # STE

・実装苦労話
STEの実装で苦労した点はSTEを実装しなくても動くことですね…。
勾配が流れる範囲では学習するのでぱっと見問題ないように見えます。
ただ逆伝搬が止まるので最終的な正解率は低くなります。
MNISTでは未学習で10%ぐらい、ちゃんと学習すると96%ぐらいの正解率になるのですが、STEが一部しか実装できてない時は86%ぐらいの正解率だったりしてBitLinearはそんなもんなのか？それとも実装が間違っているのか？といった事がありました…。
一応本実装ではただのLinear層とBitLinear層を比較してほぼ同じ正解率になることを確認しています。

グループ量子化

力尽きました。
BitLinearの計算ですがグループ単位に分けて計算することで並列計算でき高速化できますよ、というものです。
githubの他の方のコードでは実装しているものもありましたが、本記事では省略します。

Q&A

Q. 重みだけど結局小数で保存される？
A. 論文で混合精度トレーニングと記載がありました。これは学習可能な重み自体や勾配、オプティマイザーは高精度形式（小数値）で保存され、学習の精度を担保しているとの事。
ただ、高精度な重みは順伝搬で2値化(3値化)されるので、推論時には使用されないとの事。
多分、学習時は小数使うけど推論時は2値化(3値化)後の重みだけでよくなるから問題ないよ、みたいな内容かと

MNISTによる検証

BitLinearの実装コードと検証で使ったコードの全体はgithubを見てください。
比較用のモデルは以下です。(TensorflowのコードのみでTorchはgithubを見てください)

models = []
units = Linear層のニューロン数
layers = 重ねる層の数

# --- dense
m = tf.keras.models.Sequential()
m.add(kl.Flatten(input_shape=(28, 28)))
for _ in range(layers):
    m.add(kl.LayerNormalization())
    m.add(kl.Dense(units, use_bias=False))
    m.add(kl.Activation("relu"))
m.add(kl.Dense(10))
models.append(["Dense", m])

# --- 1bit
m = tf.keras.models.Sequential()
m.add(kl.Flatten(input_shape=(28, 28)))
for _ in range(layers):
    m.add(BitLinear(units, "1bit", flg_before_linear=False))
    m.add(kl.Activation("relu"))
m.add(kl.Dense(10))
models.append(["BitLinear 1bit", m])

# --- 1.58bit
m = tf.keras.models.Sequential()
m.add(kl.Flatten(input_shape=(28, 28)))
for _ in range(layers):
    m.add(BitLinear(units, "1.58bit"))
    m.add(kl.Activation("relu"))
m.add(kl.Dense(10))
models.append(["BitLinear 1.58bit", m])

活性化関数がないと学習できないのでBitLinearは "BitLinear -> ReLU" としました。
同じ層構成にするためにDenseは "LayerNormalization -> Dense(use_bias=False) -> ReLU" としています。

また比較はGithubの examples/mnist_tf.py, examples/mnist_torch.py の compare 関数を実行した結果を載せています。

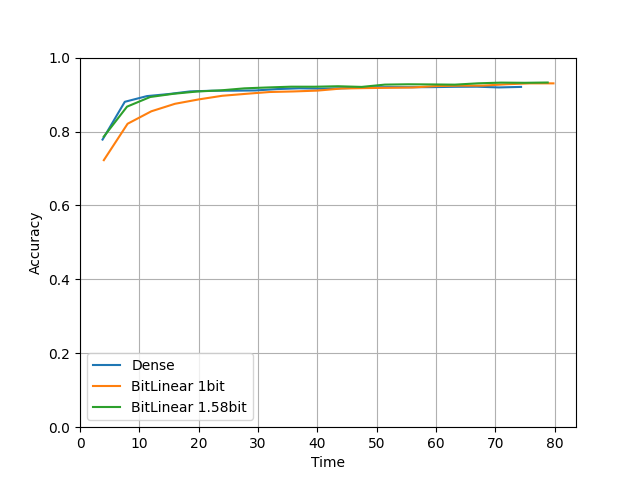
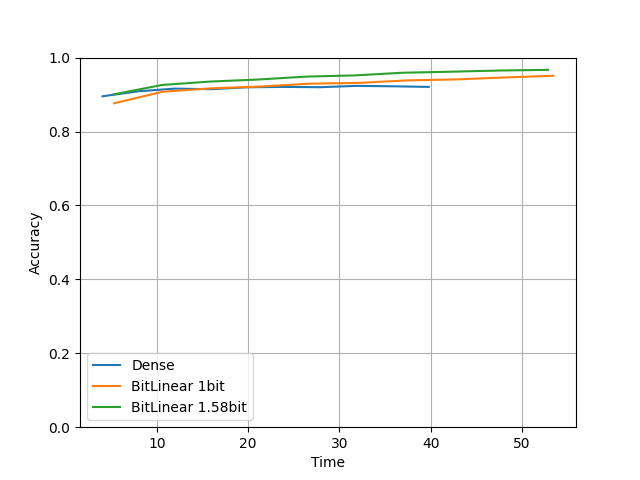
比較1. Baselineっぽいモデル

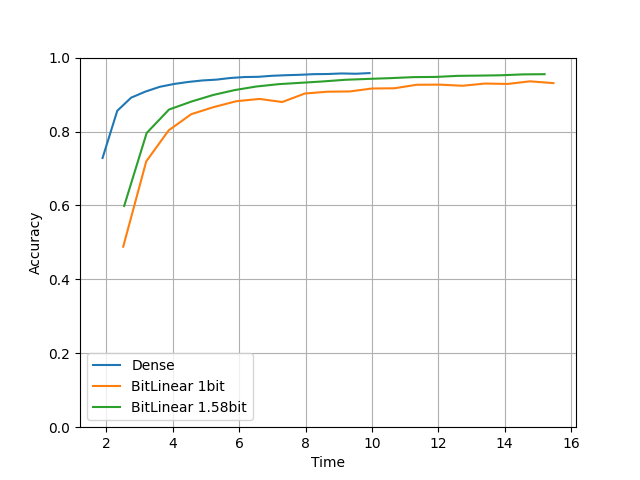
compare(units=64, layers=5, lr=0.0001, epochs=20) を実行した結果です。
実装中によく試した値です。

横軸が時間、縦軸がテスト用データの正解率です。

・Tensorflow

Figure_00.png

・Torch

Figure_01.png

TensorflowとTorchでなぜか結果がそこそこ違いました…。
学習時間はTensorflowだとDenseモデルの方が半分ぐらい早いですね。
Torchは同じぐらいですが、全体的にTensorflowより時間がかかっています。

精度はBitLinearは量子化しているにもかかわらずちゃんとDenseモデルと同じ精度になってますね。
1.58bitのモデルは元のDense層をわずかに超えていそうなきもします。
また1bitより1.58bitの方がちゃんと精度が高いですね。

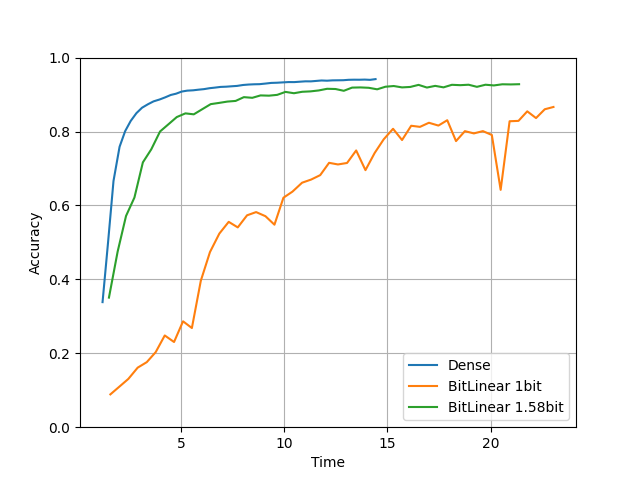
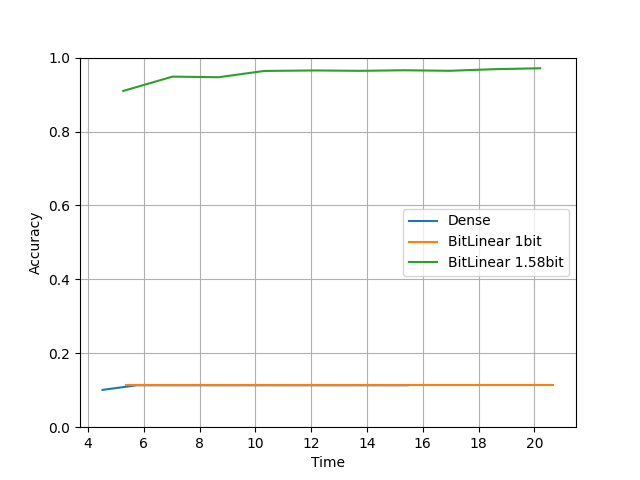
比較2. 小さいモデル

compare(units=16, layers=3, lr=0.0001, epochs=50) を実行した結果です。
units=16, layers=3 と小さいモデルです。

・Tensorflow

Figure_1.png

・Torch

Figure_2.png

精度に関して、BitLinearは量子化しているにもかかわらずちゃんとDenseモデルと同じ精度になってますね。(TensorflowのBItLinear 1bit は微妙ですけど)

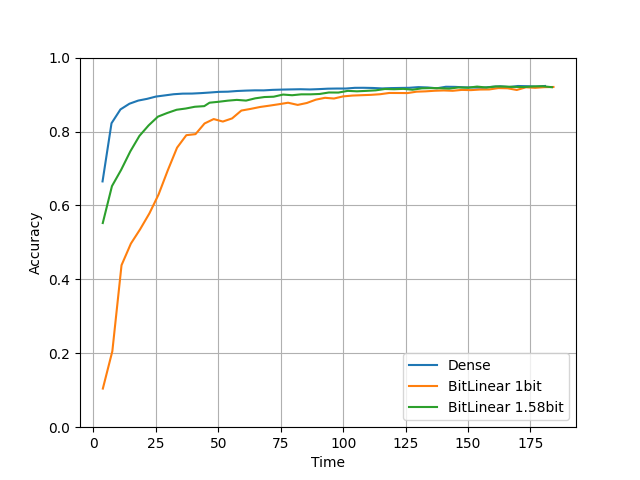
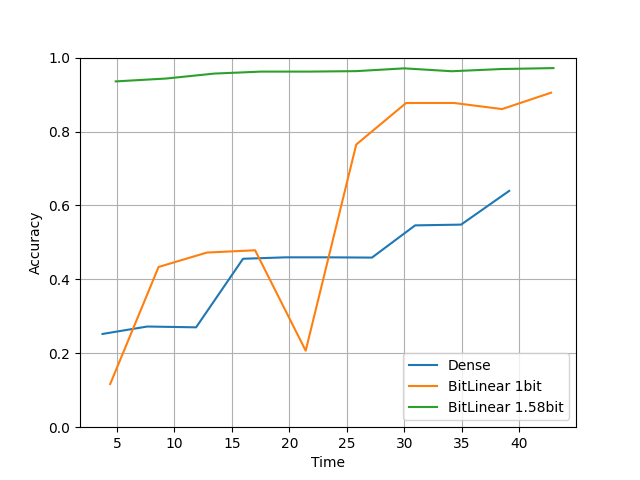
比較3. 大きいモデル

compare(units=512, layers=20, lr=0.0001, epochs=10) を実行した結果です。
units=512, layers=20 とモデルを大きくしました。

・Tensorflow

Figure_3.png

・Torch

Figure_4.png

なんとBitLinearモデルがDenseモデルよりも好成績を収めてます！
時間はDenseモデルよりかかっていますが論文通り精度が上がる結果が見れたのは良かったです。
またなぜかこっちはTorchよりTensorflowの方が時間がかかっています。

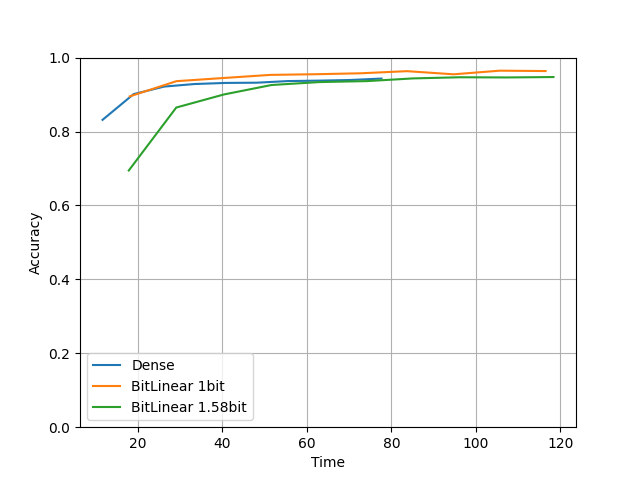
比較4. 学習率が大きいモデル

compare(units=128, layers=10, lr=0.01, epochs=10) を実行した結果です。
学習率を lr=0.0001 → lr=0.01 と大きくしました。

・Tensorflow

Figure_5.png

・Torch

Figure_6.png

論文にあった通りBitLinearは高い学習率でも安定して学習できていますね。

おわりに

論文ではTransformer(LLM)を想定しているのでMNISTの結果はあくまで目安でしかありません。
しかし、論文で言われている内容と似た結果が再現できたのは良かったです。
ただ速度は何とも言えず、量子化と逆量子化のタイミングが腑に落ちないのでまだ何かあるかもしれません。
量子化に時間がかかっているような？
多分実際には学習後にweightsを量子化して固定化する処理を入れる想定かな？

  1. DreamerV2の論文であった手法ですね ↩

15
8
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
15
8