ABC024-D 動的計画法

この問題が2020年新年初AC && 初自力黄色dificultyACだったので解説記事に書いてみることにしました。

問題

問題の概要

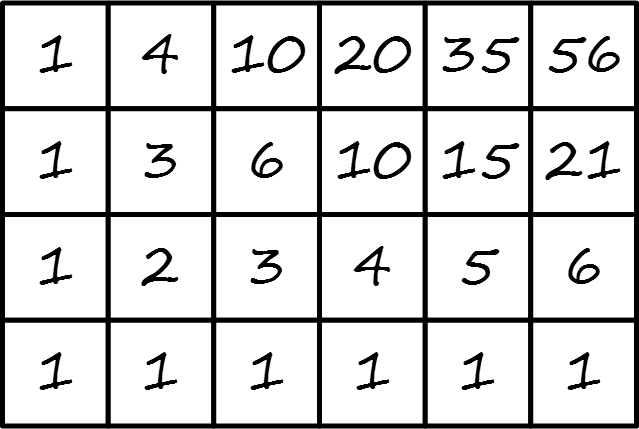
上図のように左のマスト下のマスを足した値をmod(10^9+7)で割った余りがそのマスの値となるような10^8×10^8の大きな方眼紙がある。この時「あるマス」の値(A)とあるマスの上のマスの値(B)とあるマスの左のマスの値(C)が与えられるのであるマスの座標を求めよという問題である。
例えばA=15、B=35、C=21の時は下図のような状態であるので(4,2)を出力すれば良い。

考察

問題名に動的計画法とあるものの、動的計画法をそのまま使うことはできなさそう

→一旦modは忘れて考えてみる

→それぞれのマスを(x,y)とするとその値は$x+yCx$と表せることにすぐ気付く（これは最短距離と同じ要領で）

→つまり答えを(r,c)とすると$A=r+cCr$、$B=r+c+1Cr+1$、$C=r+c+1Cr$である。

→コンビネーションは前後の関係が深いので、これらの値の関係が気になる。

→コンビネーションの前後関係の等式などを示す時には定義に帰るの一般的なので、とりあいずコンビネーションの定義に返ってみる。

→$A=(r+c)!/r!c!$、$B=(r+c+1)!/(r+1)!c!$、$C=(r+c+1)!/r!(c+1)!$である

→これを変形すると
$(r+c+1)/(c+1)=B/A$
$(r+c+1)/(r+1)=C/A$

→これはただの連立方程式なので解けて(c,r)が求められる！！

→これを解いて
$r=(AC-CB)/(CB-AB-AC)$
$s=(AB-BC)/(BC-AC-AB)$
(B,Cの対称性)

→こうして無事modを考えない場合の解法ができた

→じゃあmodを考えたらどうなるか

→結局modでも4則演算は成り立つのでmodint(mod内での四則演算が使える構造体)を同じように使い計算できる！

→modintはei1333氏のライブラリを拝借して無事AC!!!

自分の解答

最後に

初の黄色difficultyACなので嬉しくて記事化しました。読んでくれた方はありがとうございました。参考になれば幸いです。