LoginSignup
36
33
@phyblas(雛星 φυβλας)

MNIST手書き数字データをnumpyで書いたロジスティック回帰で学習して結果を分析する

Last updated at Posted at 2017-10-01

はじめに

最近機械学習について勉強し始めました。

色んな本を読んで、自分でも実装してみて、色々わかるようになりましたので、今回は自分が勉強してわかるようになったことをここで記録してみたいと思っています。

まずは機械学習の重要な基礎ともいえるロジスティック回帰の実装し方から始めたいと思います。

sklearnとかを使ったら簡単に実装できますが、numpyでスクラッチから書いた方が中身が理解できて、いい勉強になるはずです。

そう考えて、この記事では自分なりにロジスティック回帰のモデルをnumpyで書いてみます。

そしてMNISTの手描き数字データで効果のテストをさせてみます。

MNISTデータを学習するにはニューラルネットワークの方が効果的のはずですが、ニューラルネットワークの基礎はロジスティック回帰ですから、まずロジスティック回帰から把握しなければ歩き続けにくいです。

概要

この記事で書く内容はこのとおりです

  • MNISTデータの取得と可視化
  • 訓練データと検証データの分割
  • ロジスティック回帰モデルの実装
  • モデルをMNISTデータに使う
  • 過学習注意
  • 重みの分析
  • 混同行列
  • 交差検証
  • サンプル不足の場合

MNISTデータの取得

MNISTデータは数万枚の手書き数字の画像です。取得の方法は色々ありますが、今回はsklearnを通じてhttp://openml.org からデータを取得します

mnistデータの取得
import numpy as np
from sklearn import datasets
mnist = datasets.fetch_openml('mnist_784')
X,y = mnist.data,mnist.target
X = X/255.

print(X.shape) # (70000, 784)
print(y.shape) # (70000,)
print(y) # [ 0.  0.  0. ...,  9.  9.  9.]

mnist.dataは鉛筆の濃さを示す0~255の数字であり、高ければ黒で、低ければ白とされています。学習に適応とするように255で割ります。これで0~1になります。28×28の画像だから全部784列。

mnist.targetは正解を示す0~9の数字。

MNISTデータの可視化

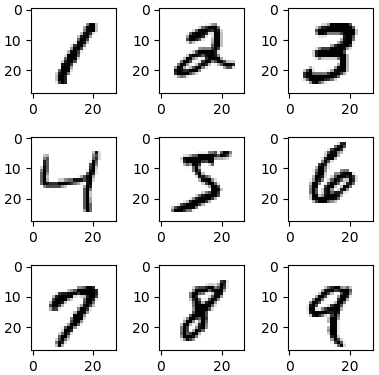
数字の絵に見えるために、28×28にreshapeする必要があります。

ここではmatplotlibで一部の数字を表示します。

mnistデータの可視化
import matplotlib.pyplot as plt
for i in range(1,10):
    plt.subplot(330+i)
    plt.imshow(X[30+i*6500].reshape(28,28),cmap='gray_r')
    plt.show()

そして手書き数字の画像が出ます。

123456789

訓練データと検証データの分割

過学習を防ぐために全部のデータを学習に使うのではなく、データを分割して、一部のデータを検証のために使うという方法がよく使われています。

今回は5分の1のデータを検証データにしましょう。

データは.targetにある数字によって0から9まで並んでいるため、分割の前にまずはシャッフルしなければなりません。numpyのrandom.permutationを使うといいです。

データの分割
n = len(X)
s = np.random.permutation(n)
nn = int(n/5)
X_kunren,X_kenshou = X[s[nn:]],X[s[:nn]]
y_kunren,y_kenshou = y[s[nn:]],y[s[:nn]]

その他に、sklearnを使うという方法もあります。一行だけで済みますので、とても簡潔。

train_test_split
from sklearn.model_selection import train_test_split
X_kunren,X_kenshou,y_kunren,y_kenshou = train_test_split(X,y,test_size=0.2)

ちなみに、昔はtrain_test_splitはcross_validationというサブモジュールに所属していたが、cross_validationはもはや破棄するため、今はmodel_selectionサブモジュールの中のtrain_test_splitを使ったほうがいいです

実装の概念

ロジスティック回帰の実装が色々詳しく説明しなければならないことがいっぱいあります。今回で使うのは

  • 確率的勾配降下法
  • ミニバッチ
  • 早期終了
  • 損失関数
  • 交差エントロピー
  • ワン・ホット
  • ソフトマックス関数

これらの内容は詳しく説明すれば長くなりますが、キーワードで検索すればすぐ見つかるはずのため、ここではアイカツ・・・じゃなくて、割愛します。

ここではまずは今回で使うロジスティック回帰モデルの設計

  • 損失関数に交差エントロピーを使う
  • 大量のデータがあるのでミニバッチを使う
  • ミニバッチを一周終わったら、検証データに対する予測正確度を計算する
  • 学習が終わる条件は、予測正確度がもう随分の間上がっていないこと
  • 後で見るために毎回算出された損失と予測正確度を登録する
  • 検証データを渡さない場合は、代わりに訓練データ自体を同時に検証データに使う
  • 学習が終わったら一番高い予測正確度を与えた時の重みを採用する

クラスの定義

私はコードを書いていた時に、無邪気に物事を勉強しているAI少女の姿が浮かんできました。それで、あぴミクというMMDモデルを使ってこの画像を作りました。

学習中

なので、初音ミクをイメージキャラとして使わせていただくことにします。モデルのクラスの名前もMikumikukaikiにします。

ロジスティック回帰モデル
class Mikumikukaiki:
    def __init__(self,gakushuuritsu):
        self.gakushuuritsu = gakushuuritsu # 学習率

    def gakushuu(self,X,y,kurikaeshi,n_batch=0,X_kenshou=0,y_kenshou=0,patience=0):
        n = len(y) # データの数
        # もし検証データが渡されなければ、代わりに訓練データを検証データにも使う
        if(type(X_kenshou)!=np.ndarray):
            X_kenshou,y_kenshou = X,y
        # バッチの数が指定されていないか、データの数より多い場合、ミニバッチをしないことにする
        if(n_batch==0 or n<n_batch): 
            n_batch = n
        self.n_group = int(y.max()+1) # 種類の数
        y_1h = y[:,None]==range(self.n_group) # 正解ラベルの配列をone-hotにしておく
        self.w = np.zeros([X.shape[1]+1,self.n_group])
        # 毎回の損失と訓練データに対する正確度と検証データに対する正確度を記録するためのリスト
        self.sonshitsu = []
        self.kunren_seikaku = []
        self.kenshou_seikaku = []
        saikou = 0 # 今までの最高の正確度
        agaranai = 0 # 正確度が何回上がっていない
        for j in range(kurikaeshi):
            s = np.random.permutation(n)
            for i in range(0,n,n_batch):
                Xn = X[s[i:i+n_batch]]
                yn = y_1h[s[i:i+n_batch]]
                phi = self.softmax(Xn)
                eee = (yn-phi)/len(yn)*self.gakushuuritsu
                self.w[1:] += np.dot(eee.T,Xn).T
                self.w[0] += eee.sum(0)
            
            seigo = self.yosoku(X)==y
            kunren_seikaku = seigo.mean()*100 # 訓練データに対する正確度
            seigo = self.yosoku(X_kenshou)==y_kenshou
            kenshou_seikaku = seigo.mean()*100 # 検証データに対する正確度
            
            
            if(kenshou_seikaku > saikou):
                # 正確度が以前より高くなるとその値を取っておく
                saikou = kenshou_seikaku
                agaranai = 0
                w = self.w.copy()
            else:
                agaranai += 1 # 上がらなければ、カウント
            
            self.kunren_seikaku += [kunren_seikaku]
            self.kenshou_seikaku += [kenshou_seikaku]
            self.sonshitsu += [self.entropy(X,y_1h)]
            
            print(u'%d回目、正確度%.3f%%、最高%.3f%%'%(j+1,self.kenshou_seikaku[-1],saikou))
            
            if(patience!=0 and agaranai>=patience):
                break # 正確度が何回たっても上がらなければ学習が終わる
                
        self.w = w # 最後に取っておいた重みを採用する

    def yosoku(self,X):
        # 予測値を計算する
        return (np.dot(X,self.w[1:])+self.w[0]).argmax(1)

    def softmax(self,X):
        # ソフトマックス関数で確率を計算する
        h = np.dot(X,self.w[1:])+self.w[0]
        exp_h = np.exp(h.T-h.max(1))
        return (exp_h/exp_h.sum(0)).T

    def entropy(self,X,y_1h):
        # 交差エントロピーを計算する
        return -(y_1h*np.log(self.softmax(X)+1e-7)).mean()

モデルにMNISTデータを学習させる

学習
gakushuuritsu = 0.24 # 学習率
kurikaeshi = 1000 # 学習が終わらない場合の繰り返す回数
n_batch = 100 # ミニバッチのサイズ
patience = 10 # 正確度が何回上がらなければ学習が終わる
mmk = Mikumikukaiki(gakushuuritsu)
mmk.gakushuu(X_kunren,y_kunren,kurikaeshi,n_batch,X_kenshou,y_kenshou,patience)

# 学習進歩のグラフを描く
plt.figure(figsize=[8,8])
ax = plt.subplot(211)
plt.plot(mmk.sonshitsu,'#000077')
plt.legend([u'損失'],prop={'family':'AppleGothic','size':17})
plt.tick_params(labelbottom='off')
ax = plt.subplot(212)
ax.set_ylabel(u'正確度 (%)',fontname='AppleGothic',size=18)
plt.plot(mmk.kunren_seikaku,'#dd0000')
plt.plot(mmk.kenshou_seikaku,'#00aa00')
plt.legend([u'訓練',u'檢證'],prop={'family':'AppleGothic','size':17})
plt.show()

学習進歩

結果を見れば、92%くらいの正確度に到達しました。ロジスティック回帰を使っただけでもこんなによくできましたが、ニューラルネットワークを使わったらもっといい結果になるはずです。

正解

過学習にならないように

ちなみに、もし検証データに対する正確度が下がり始めた時に止まらずに1000回まで続ければ、こんな結果になります。

過学習

これは過学習に陥るということです。訓練データに対する正確度はどんどん上がっていくものの、検証データに対する正確度は下がっていくというあまり望ましくない現象。同じ物の勉強を繰り返しすぎると逆に悪い結果になる。多分人間も同じ。

重みを分析する

学習した後、予測に一番適する重みとバイアスはもらえます。その重みとバイアスは今.wという属性にあります。w[0]はバイアスなので重みではない。w[1]からw[784]までを28×28にreshapeして表示します。

まずは0の重みです。

重みの表示
plt.imshow(mmk.w[1:,0].reshape(28,28),cmap='gray_r')
plt.show()

重み123456789

この重みは鉛筆の濃さの値とかける値であり、0だと予測する可能性に対するその部分の貢献を表します。つまり、重みが大きければ、その部分に鉛筆が書かれると、0である可能性が大きく上がると判断されます。

そして他の数字の重みも見ましょう。

重みの表示
for i in range(1,10):
    plt.subplot(330+i)
    plt.imshow(mmk.w[1:,i].reshape(28,28),cmap='gray_r')
plt.show()

重み123456789

混同行列

次はどこが間違いやすい部分なのかを検査します。よく使われる方法として、混同行列（混合行列とも）を作ります。

混同行列は予測結果と正解を比較する行列です。これを使ったらどの数字がよくどの数字に誤認されることはわかります。

混同行列を作る関数はこんな風に定義できます

混同行列
def confusion_matrix(y1,y2):
    n = max(y1.max(),y2.max())+1
    return np.dot((y2==np.arange(n)[:,None]).astype(int),(y1[:,None]==np.arange(n)).astype(int))

sklearnにはすでに混同行列を作る関数を持っています。これを使ってもいいですね。

sklearnのconfusion_matrix
from sklearn.metrics import confusion_matrix

どっちを使っても結果は同じです。

混同行列
t = mmk.yosoku(X_kenshou)
conma = confusion_matrix(y_kenshou,t)
for c in conma: print(c)

結果

[1276    0    4    2    3    9    8    3    6    1]
[   0 1556   11    4    1    5    0    4   17    6]
[   9   16 1225   21   11    3   15   16   26    6]
[   4   12   33 1269    0   45    3   17   34   10]
[   5    7   11    2 1245    3   16    5   12   56]
[  12    6   16   44   10 1105   25   10   39   13]
[  12    3    9    0    5   16 1343    2    4    3]
[   6    4   20    5   14    1    1 1377    1   32]
[   6   34   12   36    7   24   10    5 1242   14]
[  10    6    6   20   35   12    1   46   10 1273]

このままではわかりにくいので、よくわかりやすく見えるように、次は色をつけます。このような関数を定義して使います。

混同行列の可視化
import matplotlib as mpl

def plotconma(conma,log=0):
    n = len(conma)
    plt.figure(figsize=[9,8])
    plt.gca(xticks=np.arange(n),xticklabels=np.arange(n),yticks=np.arange(n),yticklabels=np.arange(n))
    plt.xlabel(u'予測',fontname='AppleGothic',size=16)
    plt.ylabel(u'正解',fontname='AppleGothic',size=16)
    for i in range(n):
        for j in range(n):
            plt.text(j,i,conma[i,j],ha='center',va='center',size=14)
    if(log):
        plt.imshow(conma,cmap='autumn_r',norm=mpl.colors.LogNorm())
    else:
        plt.imshow(conma,cmap='autumn_r')
    plt.colorbar(pad=0.01)
    plt.show()

plotconma(conma,log=1)

正解は誤解よりずっと多いためcmapにlog関数を使った方が見やすい。

混同行列

こうやって見やすくなりました。

結果を見ると、4と9の間に混同することが多いってことは明らかになりました。

4を9だと勘違い

この画像の中の数字は誤認された4です。見ての通り、これは9ではない。そしてろくでもない。人間なら間違うことないはずですが、確かに9と似ているところがあるため、ミクちゃんには難しいかもしれませんね。

交差検証

訓練データと検証データの分割し方は学習の結果に影響することもあります。ただ一回分割するだけでは足りないかもしれません。なので、交差検証をやってたらいいです。

ランダムにデータをk個に分けて、1回目は1個を取って検証データに、他は訓練データにします。そして2回目はもう一個を取って同じことを繰り返し、k回続くと全てのデータは一度検証データにされたことになります。そして、そのk回の結果を纏めて分析します。こんな方法はK-分割交差検証と呼びます。

例えばデータがたった14しかない場合で、5グループに分けるとしたら、このように、茶色は検証データに、緑色は訓練データに使われます。

k-foldミクテトネル

今回は試しにMNISTデータを5個に分けて、学習進歩中の正確度の平均値をプロットして、標準偏差を誤差にします。

k-fold
gakushuuritsu = 0.24 # 学習率
n_batch = 100 # ミニバッチのサイズ
n = len(y) # 全てのデータの数
nf = 5 # 何個にする
nn = int(n/nf)+(np.arange(nf)<(n%nf)) # 各グループのデータの数
kurikaeshi = 30 # 繰り返す回数（今回は早期終了はしない）
kunren_seikaku = []
kenshou_seikaku = []
s = np.random.permutation(n)
mmk = Mikumikukaiki(gakushuuritsu)
for i in range(nf):
    X_kunren = X[s[nn[i]:]]
    y_kunren = y[s[nn[i]:]]
    X_kenshou = X[s[:nn[i]]]
    y_kenshou = y[s[:nn[i]]]
    s = np.roll(s,nn[i],0) # 回すことでデータを分割するところは毎回変わる
    mmk.gakushuu(X_kunren,y_kunren,kurikaeshi,n_batch,X_kenshou,y_kenshou)
    kunren_seikaku.append(mmk.kunren_seikaku)
    kenshou_seikaku.append(mmk.kenshou_seikaku)
kunren_seikaku = np.stack(kunren_seikaku)
kenshou_seikaku = np.stack(kenshou_seikaku)

plt.figure(figsize=[8,6])
plt.errorbar(np.arange(kurikaeshi),kunren_seikaku.mean(0),yerr=kunren_seikaku.std(0),color='#dd0000')
plt.errorbar(np.arange(kurikaeshi),kenshou_seikaku.mean(0),yerr=kenshou_seikaku.std(0),color='#00aa00')
plt.title(u'正確度 (%)',fontname='AppleGothic',size=18)
plt.legend([u'訓練',u'檢證'],prop={'family':'AppleGothic','size':17})
plt.show()

k-fold

結局のところ、やはり正確度は92%くらいです。

ちなみにsklearnにはk-foldを行うための関数もあります。もしこれを使ったらこのように簡潔に書けます。

sklearnのk-fold
from sklearn.model_selection import KFold
kf = KFold(n_splits=5,shuffle=True)
for kr,ks in kf.split(y):
    X_kunren = X[kr]
    y_kunren = y[kr]
    X_kenshou = X[ks]
    y_kenshou = y[ks]
    # ...使う部分

それに、StratifiedKFoldというクラスもあります。これを使ったらデータセット内のラベルの比率を保ったまま分割することができますが今回では必要がありません。

学習サンプル不足の場合

もし学習のためにサンプルが少なすぎたらどうなるか、こういう状況も考えてみましょう。例えば、MNISTの全て70000から7000だけ取り出してみます。

サンプルを減らす
s = np.random.permutation(len(y))
X = X[s[:7000]]
y = y[s[:7000]]

そしてまた前と同じようなK-分割交差検証を行ってみたら、こういう結果になります。

7000過学習

訓練データに対する正確度はだんだん増えますが、検証データに対する正確度は90%未満になります。つまり過学習は激しくなります。

更に、もしサンプルの数を700まで減らしたらこうなります。

サンプルをさらに減らす
s = np.random.permutation(len(y))
X = X[s[:700]]
y = y[s[:700]]

700過学習

訓練データに対する正確度は100%になりました。検証データに対する正確度もまた下がりました。もし更にサンプルが減ったらもはやこれは『その画像セットだけを予測するための学習』になります。

サンプルデータが足りないのは過学習の一番の原因となります。解決するために色んな方法がありますが、話が長くなりますので、ここで終わることにします。

終わりに

色々試してきてこの記事に纏めましたが、コードはあくまで自分がいいと思って書いたもので、実際にもっといい書き方があるかもしれません。指摘していただければ嬉しいです。

参考

使ったmmdモデル

36
33
1

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
36
33