LoginSignup
60
55

More than 1 year has passed since last update.

@perico_v1

SHAP(SHapley Additive exPlanation)についての備忘録

Posted at

背景・目的

ブラックボックス化しがちな機械学習モデルを解釈し、なぜその予測値が出ているのかの説明に役立つSHAP値について、理解を深めるべく論文や公式資料を漁りました。自分用の備忘録としてこちらに内容をまとめておきます。

SHAPとは何か?

  • 正式名称はSHapley Additive exPlanationsで、機械学習モデルの解釈手法の1つ
    • なお、「SHAP」は解釈手法自体を指す場合と、手法によって計算された値(SHAP値と呼ぶこともある)を指す場合がある
  • NIPS2017 1にて発表された
  • それまでに存在した解釈手法(Additive Feature Attribution Methods。 LIMEの基本アイデア)に協力ゲーム理論のShapley Valueを導入して改良したもので、計算効率の向上と実用上の望ましい数学的性質(後述)を兼ね備えている
    • 協力ゲーム理論において、Shapley Valueとは各プレイヤーの貢献度合いに応じて利益を分配する指標のこと
    • そこで、機械学習モデルの各特徴量をプレイヤーに見立ててShapley Valueを計算することで各特徴量の貢献度合いを評価しようというもの
  • 各特徴量のSHAP値はサンプルのそれぞれのレコードに対して求められる
    • そのため、特定のレコードに対して予測結果の解釈が可能(ミクロ的解釈)
    • また、サンプル全体で各特徴量のSHAP値の分布や平均を見ることで、モデル内での各特徴量の予測値に対する影響の仕方を把握できる(マクロ的解釈)

Additive Feature Attribution Methodsとは何か?

  • Additive Feature Attribution Methodsとは、特徴量の線形関数を用いた機械学習の解釈手法のこと
  • 線形回帰モデルの解釈が容易なことから、機械学習モデルにおいても各データに対して特徴量と予測結果の線形モデルを作り、特徴量が予測に与える影響を定量評価しようとする手法
  • 元の特徴量($x_{i}$)から、その特徴量の存在有無を示すバイナリ値($z_{i}^{'}$)に代えて扱う

定義式は以下の通りです。

\begin{align}
g(z^{'})&=\phi_{0}+\sum_{i=1}^{M}\phi_{i}z_{i}^{'}\\
&(=bias+\sum contribution \space of \space each \space feature)
\end{align}

ここで、$g(z^{'})$は元の予測モデル$f(x)$に対する局所的な代替モデルを表し、$\phi_{i}$は特徴量$i$の有無によってどれだけ最終的な予測結果に影響があるかを示しています。

Shapley Valueとは何か?

  • 協力ゲーム理論 2において利益分配の基準として用いられる指標の1つ
  • 複数のプレイヤーが協力して得た利益を各プレイヤーの貢献度に応じて分配する際に、どのプレイヤーにどれだけ分配すればよいかを表す
  • プレイヤー $i$ が加わることによって生じる追加的な貢献度を限界貢献度と呼び、この限界貢献度を用いて計算される
    • (参考) 限界貢献度とは
      • プレイヤー $i$ が加わることによって生じる追加的な貢献度のこと
      • プレイヤーの部分集合$S$に対して、$v(S)$をSのメンバーが協力することによって獲得できる利益とした時、任意の$i\in N$と任意の部分集合$S\subseteq N\setminus \{ i \}$ 3に対して、プレイヤー$i$の限界貢献度は$v( S\cup \{ i \} )-v(S)$で表される
  • プレイヤー$i\space(\in N)$のShapley Valueは以下で定義される ( $|S|$ は任意の部分集合$S\subseteq N$に対して$S$の要素数)$$\phi_{i}(v)=\sum_{S\subseteq N\setminus \{i\}}\frac{|S|!(n-|S|-1)!}{n!}(v(S\cup \{i\})-v(S))$$
  • アルバイトゲームとShapley Valueに記載されているアルバイトの例が非常にわかりやすい

機械学習モデルの解釈を目的とした場合のSHAP値

  • 機械学習モデルの解釈においては、協力ゲーム理論における各プレイヤーを機械学習モデルの各特徴量に置き換えてSHAP値を計算する
  • ある特徴量$i$以外の全ての特徴量の組み合わせについて、予測モデルの出力$f_{x}$が特徴量$i$を含むことで生じる予測結果$f_{x}$の差を評価する

計算式は以下の通り(前述の式と同じ)です。

\phi_{i}=\sum_{S\subseteq N\setminus \{i\}}\frac{|S|!(n-|S|-1)!}{n!}(f_{x}(S\cup \{i\})-f_{x}(S))

ここで、$S$は特徴量$i$を除いた特徴量の部分集合であり、$f_{x}(S)$は特徴量の集合$S$の元での予測結果の期待値です。

f_{x}(S)=E[f(x)|x_{S}]

SHAPの3つの性質

SHAPには以下3点の性質があり、この3点を満たす説明モデルはただ1つとなることがわかっています (SHAPの主定理)。

  • 1: Local accuracy
    • 説明対象のモデル予測結果 = 特徴量の貢献度の合計値(SHAP値の合計) の関係になっている
    • $f(x)=g(x^{'})=\phi_{0}+\sum_{i=1}^{M}\phi_{i}x_{i} ^{'}$
  • 2: Missingness
    • 存在しない特徴量( $z_{i}^{'}=0$ )は影響しない
    • $x_{i}^{'}=0\Rightarrow \phi_{i}=0$
  • 3: Consistency
    • 任意の特徴量がモデルに与える影響が大きくなるようにモデルを変更した際に、その特徴量の貢献度が減少しない
    • $f_{x}^{'}(z^{'})-f_{x}^{'}(z^{'}\setminus i)\geq f_{x}(z^{'})-f_{x}(z^{'}\setminus i)$

SHAPの様々なタイプ

特定のモデルに関しては、モデル個別のSHAP(近似値)の計算手法があります。特定のモデルに特化することで計算をより高速にできる利点があります。

  • Linear SHAP
    • 線形モデルの貢献度合い計算法
    • 線形モデルの場合、SHAP値はモデルの重み係数から直接近似できる
    • $f(x)=\sum_{j=1}^{M} w_{j}x_{j}+b, \space \phi_{0}(f, x)=b$のもとで、$\phi_{i}(f, x)=w_{j}(x_{j}-E[x_{j}])$
    • 実際、重回帰モデルなどでSHAP値を出すと、回帰係数×変数の値 とSHAP値が一致
  • Tree SHAP
    • 決定木ベースのモデルに対する手法
  • Deep SHAP (DeepLIFT + Shapley Values)
    • 深層学習モデルに特化した手法

SHAP値の手計算

シンプルな決定木を用いて、実際にSHAP値を手計算してみます。 SHAP値がどのように計算されているかを大まかに把握することが目的なので、決定木自体はpythonで作成し、特に精度にはこだわっていません。

以下は利用スクリプトです。(※Jupyter Notebookを利用しています。)

# ライブラリの読み込み
import numpy as np
import pandas as pd

from sklearn.model_selection import train_test_split
from sklearn.tree import  DecisionTreeRegressor
from sklearn.metrics import mean_absolute_error

import matplotlib.pyplot as plt
%matplotlib inline
from sklearn.tree import plot_tree

# データ用意
X, y = shap.datasets.boston()
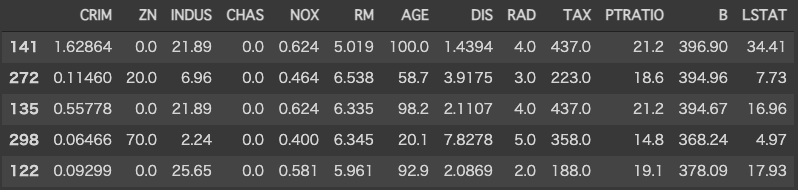
X.head()

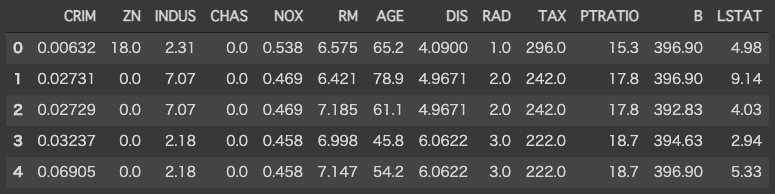
Toy dataとしてボストンの住宅価格データを用います。データの中身は以下の通りです。
image.png

続いて、決定木の作成~可視化です。

# 決定木をシンプルな構成にするため、変数を絞る
X = X.loc[:, ['CRIM', 'DIS']]

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)

# create model
model = DecisionTreeRegressor(max_depth=2) # シンプルな木にするため2階層に指定
model.fit(X_train, y_train)

print(mean_absolute_error(y_train, model.predict(X_train)).round(2))
print(mean_absolute_error(y_test, model.predict(X_test)).round(2))
# 5.56
# 6.26

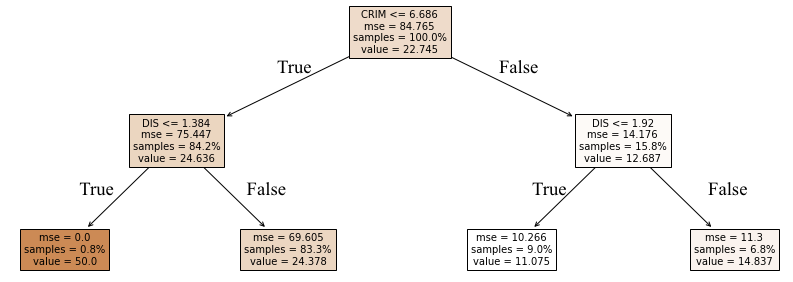
plt.figure(figsize=(16, 6))
plot_tree(model, feature_names=X.columns, filled=True, proportion=True, fontsize=10)
plt.show()

image.png

(※True/Falseのテキストは後で手動でつけたものなので、上記コードを実行しても出てきません。)
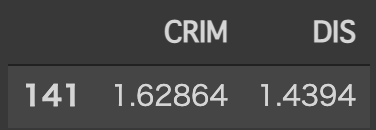
1番目の訓練データについてSHAP値を計算してみようと思うので、まず特徴量を確認します。

X_train.head(1)

image.png

次に、特徴量の組み合わせ($S$)ごとにモデル期待値を計算します。計算した結果が以下の表です。

特徴量の組み合わせ モデル期待値 ($f_{x}(S)$)
1 {特徴量なしの場合} 22.74
2 {CRIM} 24.63
3 {DIS} 17.72
4 {CRIM, DIS} 24.37

それぞれの特徴量の組み合わせごとのモデル期待値 ($f_{x}(S)$) は以下のように計算しました。
(あくまでSHAP値の計算方法のイメージを掴むことが目的であり、SHAP値が概算できれば良いものとして進めています。そのため、一部大雑把な計算になっているところがあるかと存じます。修正点があれば修正方法と併せてご指摘いただけると幸いです。)

  • 特徴量なしの場合: $f_{x}$は予測値の平均値
  • 特徴量がCRIMのみの場合
    • CRIMの情報のみわかっている場合のモデル期待値を計算するには、周辺化でDIMの影響を除外した予測値を計算する
    • CRIM = 1.62なので、決定木の最初の分岐条件はTrueでそれ以上先はないので最初の条件分岐にあるvalue=24.636(CRIM<=6.686を満たす訓練データの平均値になっている)をモデル期待値とする
  • 特徴量がDISのみの場合
    • DISの情報のみわかっている場合のモデル期待値を計算するには、周辺化でCRIMの影響を除外した予測値を計算する
    • DIS=1.43の場合は予測値は24.37, 11.07のどちらかになるので、平均をとって17.72
  • 特徴量がCRIM、DISの場合: 今回作った決定木の予測結果そのもので、24.37

上記の値を用いると、テストデータの1レコード目における、CRIM、DISそれぞれのSHAP値を手計算することができます。

例えば、CRIMのSHAP値を求める場合($i=$CRIMの場合)は以下のようになります。
特徴量のサブセットは2通りあり、

  1. $S=\{\}, |S|=0, |S|!=1, S\cup \{ i \} = \{ CRIM \}$
  2. $S={DIS}, |S|=1, |S|!=1, S\cup \{ i \} = \{ CRIM, DIS \}$

計算式と結果は以下の通りです。

\begin{align}
\phi _{CRIM}&=\frac{0!1!}{2!}[f_{x}(CRIM=1.62)-f_{x}()]+\frac{0!1!}{2!}[f_{x}(CRIM=1.62, DIS=1.43)-f_{x}(DIS=1.43)]\\
&=\frac{1}{2}(24.63-22.74)+\frac{1}{2}(24.37-17.72)=4.27
\end{align}

同様に、DISのSHAP値も計算してみます。

\begin{align}
\phi _{DIS}&=\frac{0!1!}{2!}[f_{x}(DIS=1.43)-f_{x}()]+\frac{0!1!}{2!}[f_{x}(DIS=1.43, CRIM=1.62)-f_{x}(CRIM=1.62)]\\
&=\frac{1}{2}(17.72-22.74)+\frac{1}{2}(24.37-24.63)=-2.63
\end{align}

上記の計算式から明らかではありますが、求めたSHAP値を特徴量がないときのモデル期待値(base value:$\phi_{0}$)に足していくと、予測結果になります。

\begin{align}
\phi_{0}+\phi_{CRIM}+\phi_{DIS}&=22.74+4.27-2.63\\
&=24.38\space(=f(x))
\end{align}

検算も兼ねてpythonでもSHAP値を出してみます。

# SHAP(SHapley Additive exPlanations)
import shap

explainer = shap.Explainer(model, X_train)
shap_values = explainer(X_train)
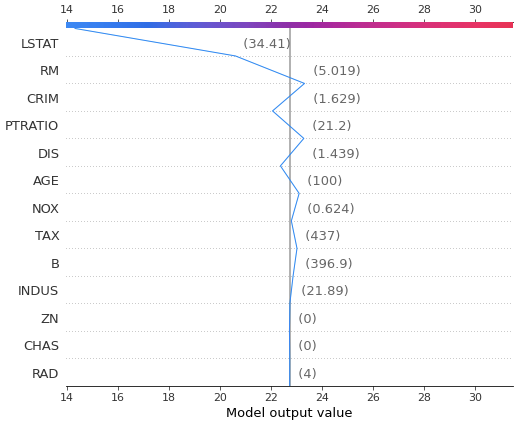
shap.plots.waterfall(shap_values[0])

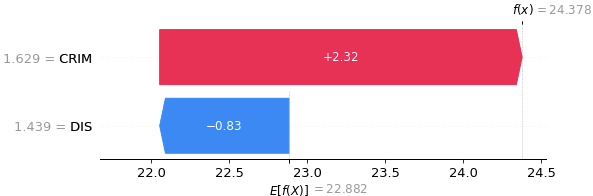
結果は以下の通りです。手計算した値はやや異なってしまったのですが、SHAP値の絶対値がCRIM>DISとなっている点と、CRIMが正でDISが負の値になっている点は一致していました。
image.png

SHAP値の取得と可視化スクリプト一式

簡易的にモデルを作り、SHAPの取得から可視化までを一通り行ってみます。可視化についてはいろいろな関数が用意されているので使い方を見ていきたいと思います。

データの準備

# ライブラリの読み込み
import numpy as np
import pandas as pd

from sklearn.model_selection import train_test_split
from xgboost import XGBRegressor

from sklearn.metrics import mean_absolute_error
from sklearn.model_selection import GridSearchCV

# SHAP(SHapley Additive exPlanations)
import shap

from sklearn.tree import plot_tree
import matplotlib.pyplot as plt
%matplotlib inline

# dataの用意
X, y = shap.datasets.boston() # ボストンの住宅価格データ
X.shape
# (506, 13)

X.head()

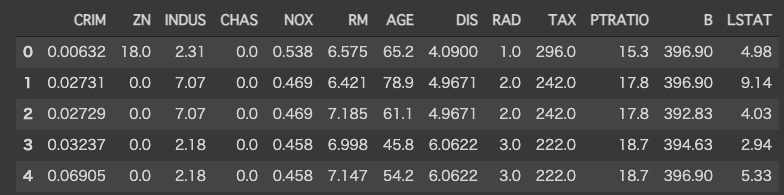
ここでもToy dataとしてボストンの住宅価格データを用います。データの中身は以下の通りです。
image.png

# 訓練データとテストデータに分ける
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)

モデル作成(XGBoost)

※SHAP値の計算・可視化が目的なので、モデルの精度などは一旦度外視しています。

params = {'n_estimators': 100,
          'max_depth': 5,
          'min_samples_split': 5,
          'learning_rate': 0.01,
          'loss': 'ls'}

xgb = XGBRegressor(**params)

params_search = {'n_estimators': [10, 100, 1000]}
grid = GridSearchCV(xgb, params_search, cv=10, n_jobs=-1, verbose=True)
grid.fit(X_train, y_train)

print('Grid best parameter: ', grid.best_params_)
# Grid best parameter:  {'n_estimators': 1000}

params = {'n_estimators': grid.best_params_['n_estimators'],
          'max_depth': 5,
          'min_samples_split': 5,
          'learning_rate': 0.01,
          'loss': 'ls'}

xgb = XGBRegressor(**params)
xgb.fit(X_train, y_train)

# 一応確認
print(mean_absolute_error(y_train, xgb.predict(X_train)))
print(mean_absolute_error(y_test, xgb.predict(X_test)))
# 0.34361747671655346
# 2.526548767717261

予測結果の確認

訓練データに対する予測結果の平均値(=SHAP値のbase value)を見ておきます。合わせて、最初の数レコードの予測値、訓練データの各特徴量の値を確認しておきます。

# 予測結果
y_pred = xgb.predict(X_train)

# 最初の5レコード分の予測値
print(y_pred[0:5].round(1))
# [14.3 24.3 17.8 22.9 20.4]

# 予測値の平均
y_pred.mean()
# 22.743422

# 訓練データの特徴量
X_train.head()

以下は訓練データの最初の数レコードの内容です。
image.png

SHAP値の計算

ここからSHAPの計算~可視化です。

explainer = shap.TreeExplainer(xgb)

# SHAP値は「shap._explanation.Explanation」で持つか、array型で持つかで出し方が少し変わる
shap_values = explainer(X_train) # shap._explanation.Explanation型の場合
shap_values_ar = explainer.shap_values(X_train) # numpy.ndarray型の場合
print('shap_values: ', type(shap_values))
print('shap_values_ar: ', type(shap_values_ar))
# shap_values:  <class 'shap._explanation.Explanation'>
# shap_values_ar:  <class 'numpy.ndarray'>

waterfall

滝グラフの形式で可視化です。

# 訓練データの1レコード目の各特徴量のSHAP値を滝グラフで可視化
shap.plots.waterfall(shap_values[0])

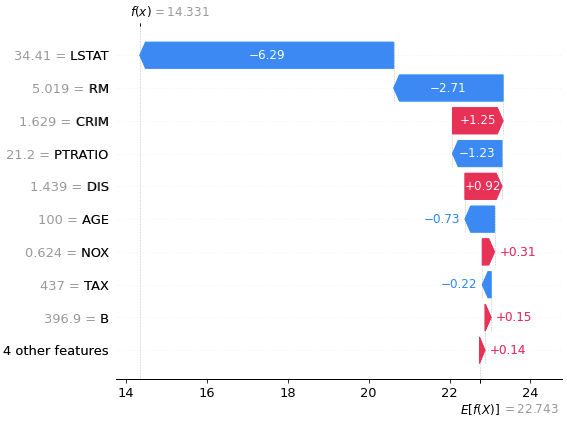
image.png
グラフ上部の$f(x)=14.331$と書かれているグレーの線が予測値を示し、グラフ左下の$E[f(X)]=22.743$と書かれている場所がbase valueです。各特徴量の棒グラフの値はSHAP値で、予測値を引き上げる特徴量は赤で示され、予測値を下げる特徴量は青で示されています。それぞれの特徴量がbase valueに対し正負どちらの方向にどの程度影響し、予測値に至ったかが直感的にわかるようになっています。

decision_plot

decision_plotという関数でも各特徴量のSHAP値と予測結果の可視化が可能です。(使い勝手が悪いのか、あまり見かけることはないグラフですが、個人的には1レコード可視化する分にはわかりやすいと思ってます。) 詳しい説明は論文著者が公開しているdecision_plotのドキュメントに載っています。

# 訓練データの1レコード目の各特徴量が予測結果に与える影響を可視化
# モデルのbase valueはグラフ中央付近のグレーの線で、グラフ上部の目盛りと折れ線の接点が最終的な予測値になっている
# 各特徴量がbase valueにどの程度作用して最終的な予測値になっているかがわかるようになっている
shap.decision_plot(explainer.expected_value, shap_values_ar[0], X_train.iloc[[0], :])

image.png

waterfallと違って、複数レコードまとめて確認することも可能です。

# 訓練データの10レコード分をdesicion_plotで可視化した場合
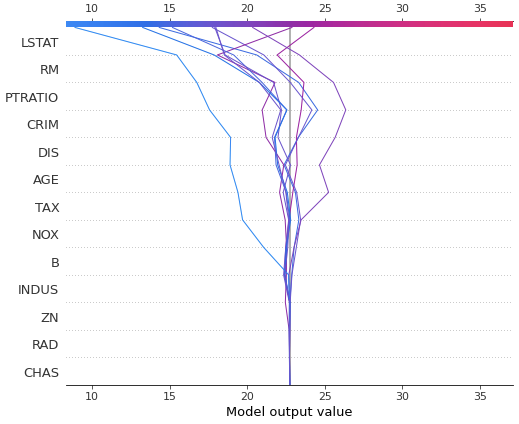
shap.decision_plot(explainer.expected_value, shap_values_ar[0:10], X_train.iloc[0:10, :])

image.png

しかし、可視化対象が多すぎると、decision_plotでは収拾がつかなくなります。

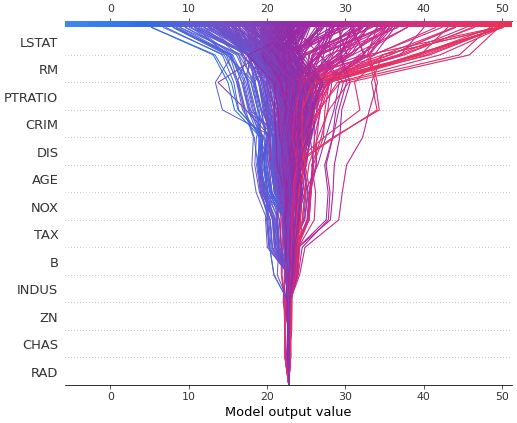
# 訓練データの全てをdesicion_plotで可視化した場合
shap.decision_plot(explainer.expected_value, shap_values_ar, X_train)

image.png

force_plot

force_plotという関数もあるので、試してみます。

# 訓練データの1レコード目の各特徴量のSHAP値を数直線上で可視化
shap.initjs()
shap.plots.force(shap_values[0])
# 以下でも同じ結果になる
# shap.force_plot(explainer.expected_value, shap_values_ar[0], X_train.iloc[0, :])

image.png

複数レコードに対してforce_plotを作成した場合は、各レコードのforce_plotが90度回転し、縦に並んだ形式で可視化されます。このグラフはインタラクティブになっており、サンプルの並び順(デフォルトではサンプルの類似度順)、縦軸の内容を変えられるようになっています。

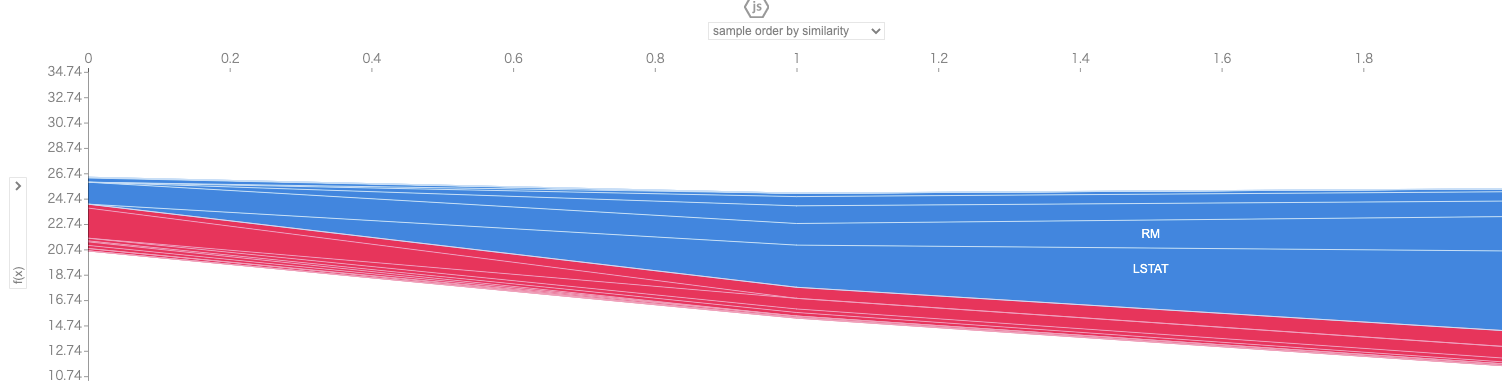
# 訓練データの初めの3レコードについてSHAP値を可視化
shap.initjs()
num = 3
shap.force_plot(explainer.expected_value, shap_values_ar[0:num], X_train.iloc[0:num, :])

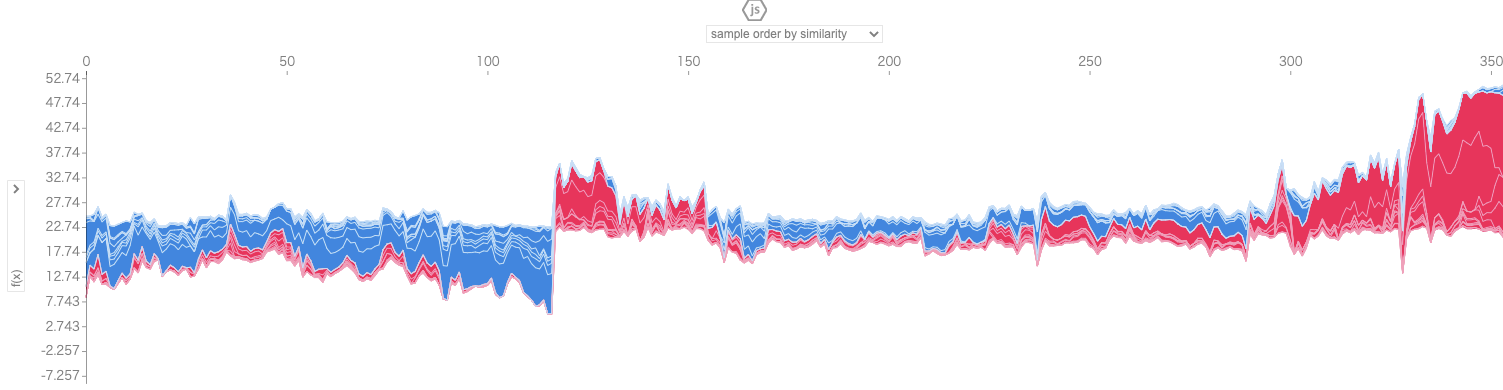
image.png

# 訓練データの全レコードについてSHAP値を可視化
shap.initjs()
shap.force_plot(explainer.expected_value, shap_values_ar, X_train)

image.png

summary_plot

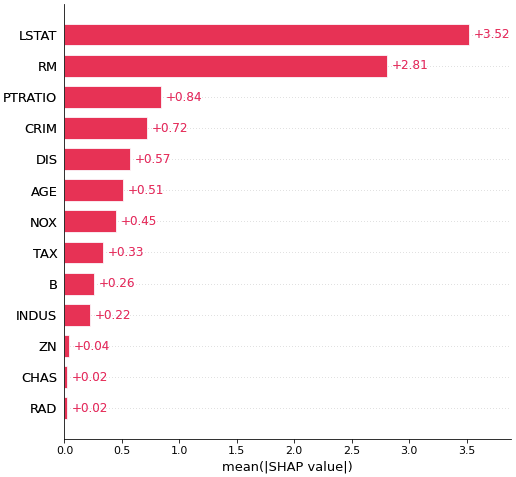
# 各特徴量のSHAP値の絶対値の平均(つまり、各特徴量の予測に対する寄与度)を棒グラフで表示
# 予測に対する寄与度が大きい順にソートされて表示される
shap.plots.bar(shap_values, max_display=20) # max_displayで表示する変数の最大数を指定

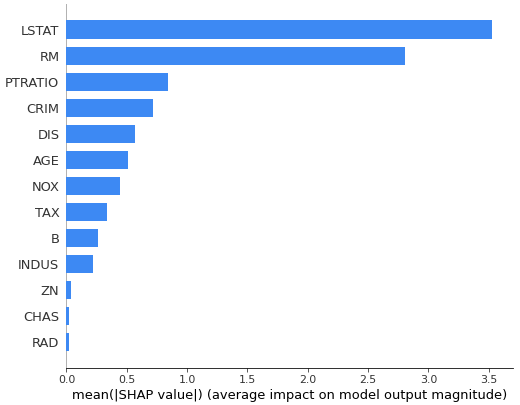
image.png

# 少し見た目が異なるが、以下でも同じグラフが作れる
shap.summary_plot(shap_values_ar, X_train, show=True, plot_type='bar', max_display=20) # max_displayで表示する変数の最大数を指定

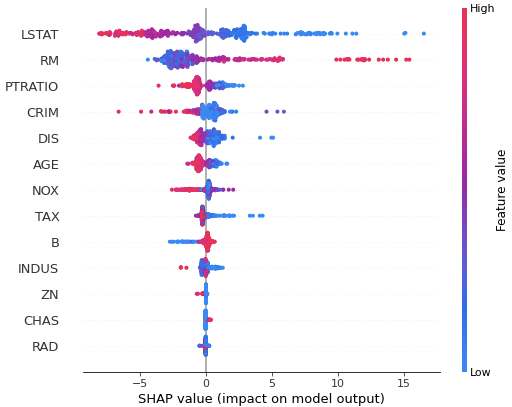
image.png

# 全サンプルについて、各特徴量のSHAP値の分布を可視化したもの
# 上記の棒グラフ同様、予測に対する寄与度が大きい順にソートされて表示される
# 色は特徴量の値の大小を表している(赤が大きくて青が小さい)
# LSTATの値が小さいほど予測値(住宅価格)は大きくなることがわかる
shap.plots.beeswarm(shap_values, max_display=20) # max_displayで表示する変数の最大数を指定

# 以下でも同じ結果が得られる
# shap.summary_plot(shap_values_ar, X_train, show=True)

image.png

dependence_plot

論文著者が公開しているdependence_plotのドキュメントが参考になります。

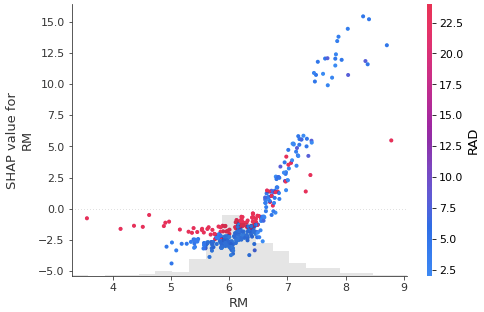
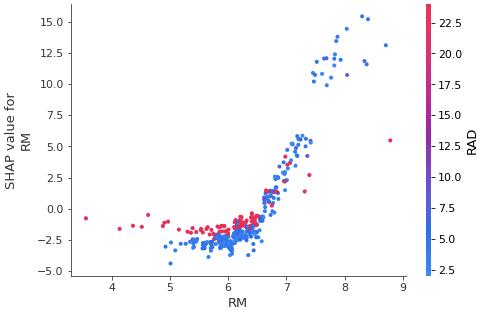
# ある1つの特徴量(今回はRM)について、訓練データ全体でのその特徴量(RM)の値と、対応するSHAP値の散布図を作成
# 横軸が特徴量の値、縦軸が対応するSHAP値
# SHAP値は予測値に対する特徴量の寄与を示すので、この図から、RMが変化したら予測値がどう変化するか読み取れる
# RMが大きいほどSHAP値は大きい、つまり、home priceが大きくなることを示している

# また、このグラフでは選択した特徴量(RM)と他の特徴量との相互作用も確認できるようになっていて
# color引数にshap値の変数を指定すると、自動的に適した変数が選択される
# 今回はRADが選ばれていて、RADの大小によって、同じRMでもSHAP値が異なることが確認できる
shap.plots.scatter(shap_values[:,'RM'], color=shap_values)

image.png

# 以下でも似たグラフが描画できる。ヒストグラムは付いてこない
shap.dependence_plot('RM', shap_values_ar, X_train, show=True)

image.png

終わりに

SHAPそのものについては調べたものの、Permutation importanceやランダムフォレストで出力される特徴量重要度などと比較したメリット・デメリット、使い分けなどについては調べきれなかったので、今後の宿題にしようと思いました。

参考文献

  1. NIPSとはNeural Information Processing Systemsの略で、1987より開催されている機械学習に関する国際会議。機械学習分野における最難関の会議の1つ。NIPS2017は2017年12月に米カリフォルニア州ロングビーチにて開催された ↩

  2. ゲーム理論は大きく「非協力ゲーム理論」「協力ゲーム理論」に分けられる。協力ゲーム理論ではプレイヤー間で協力して得られた便益をどのように分配するかを扱う ↩

  3. $\setminus$は差集合を意味し、$N\setminus \{ i \}$は集合$N$から$i$を除いた集合を指す ↩

60
55
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
60
55