【独自射影構造によるLLM】N4: Nova Nox Neural Network Flash Technical Report

※執筆者のデザインしたアイコンとなっています。ご自由にご利用ください。

はじめに

川面にリップが灯り、そよ風がかすかに温かみを帯びる今日この頃、皆様いかがお過ごしでしょうか？
六花　牡丹（りっか　ぼたん）と申します。
個人的に人工知能技術、特にアーキテクチャや計算機構に関する研究を行っており、その簡易的な技術報告として、本記事を執筆させていただきます。
本記事では、Attention Mechanismをベースとしつつ、Attention MechanismにSimplified Selective Mechanismを統合することで、高い表現力および適応性を付加した機構である、
N4: Nova Nox Neural Network
のご説明と、
ASGG: Adaptive Swish GELU Gating
という活性化関数を用いたMLPのご説明となります。

本記事に記載のモデルは、
GitHub Repository(N4 pytorch implementation)
からご利用いただけます。

N4CがCausal Language Modelとなっていますので、こちらのclassを用いて学習などしてみてください。

拙筆ではございますが、皆様のお役に立つことを心から願っております。
未熟者故、記事中にて誤記・欠落などが見られることがございます。
もし発見しました場合には、コメント等にてご指摘いただきますようお願い申し上げます。

六花牡丹のX(Twitter)アカウント
ここで最新の進捗や技術に関する情報（時々近況）を共有していきますので、もしよろしければフォローなどよろしくお願いいたします。（Also, question, issue, correction request, joint research, recruit, etc...）

論文と比較するとデータの数が少なく、
簡易的な技術報告としての位置づけとなります。

著者は趣味にて研究を継続しているため、
大規模モデルを作成することができません。
企業や研究所の方で計算機リソースがある場合は選択肢の一つとしていただけると幸いです。

執筆動機

独自LLMの技術展開によって、日本国の一研究者においても、実用可能なLLMの機構を創造することは可能であることを周知するとともに、諸外国と比較して報告件数の伸び悩む分野に対して興味関心を高める契機とし、もって日本国の科学技術発展に寄与することを目的とする。

対象とする読者

• pythonを用いたプログラミングは最低限行うことが可能である
• CNNやRNN、Transformerの構造についてはある程度理解している
• 最新のアーキテクチャを用いた研究・開発を行いたい
• 新しい計算機構を有するLLMを開発したい

独自LLM（N4: Nova Nox Neural Network）の技術報告

N4: Nova Nox Neural NetworkはAttentionやRNN、Mambaのようなネットワークアーキテクチャの一種です。
ベースとなっているのはAttentionであり、そこにSimplified Selective Mechanismを加え、Induction Gateのような選択的抽出機能を付与し、かつRoPE: Rotary Position Embeddingなどのような位置埋め込みを同時に実現したものとなります。
これにより、Attn_Matrixは単なるトークン間の関係性を表すのではなく、文脈を圧縮した状態とトークンとの関係を表すものとなり、高い表現力と適応性を獲得できるものと考えられます。
これだけの機能にもかかわらず、少ないコードおよび演算で実現可能であることを示し、かつN4モデルを利用するためのサンプルコードも示します。

本記事では以下の流れに沿って解説を行っていきます。

1. お忙しい方へ（要約）
2. Attentionとは
3. 選択的抽出機構の数学的理解
4. Simplified Selective Mechanism
5. 位置埋め込みという視点から見たSimplified Selective Mechanism
6. ASGGによる適応性
7. N4モデルのアーキテクチャ
8. N4モデル利用のためのコード
9. 実験結果（簡易報告）
10. 議論
11. 謝辞
12. 最後に
    参考文献・記事等（リンク）

1. お忙しい方へ

N4: Nova Nox Neural Networkの概要は次の通りです。

1. Tanh Gatingおよびチャネル方向のテンソルの加算により、Simplified Selective Mechanismを実現し、多解釈性を有する文脈圧縮状態（Key）を作成し、QueryとのMatrixを作成することで表現力・適応性の向上を志向しています

2. チャネル方向のテンソルの加算時に勾配を設けることで、ALiBiのような位置埋め込みを実現しています

3. ASGG: Adaptive Swish GERU Gatingにより、適応性を向上させたMLP層を実現しています

4. DyT: Dynamic Tanh NormalizationをN4層, MLP層のpre&post normalizationとして用いることで、内部共変量シフトと層間の非線形性の偏りを効率的に防止しています

5. モダンな手法(Unet likeなresidual構造やMuon Optimizer)を用いなくてもNanoGPT（現代においてPPL（Loss）減少が最も早い言語モデル）と同等程度のPPL（Loss）減少を示しました

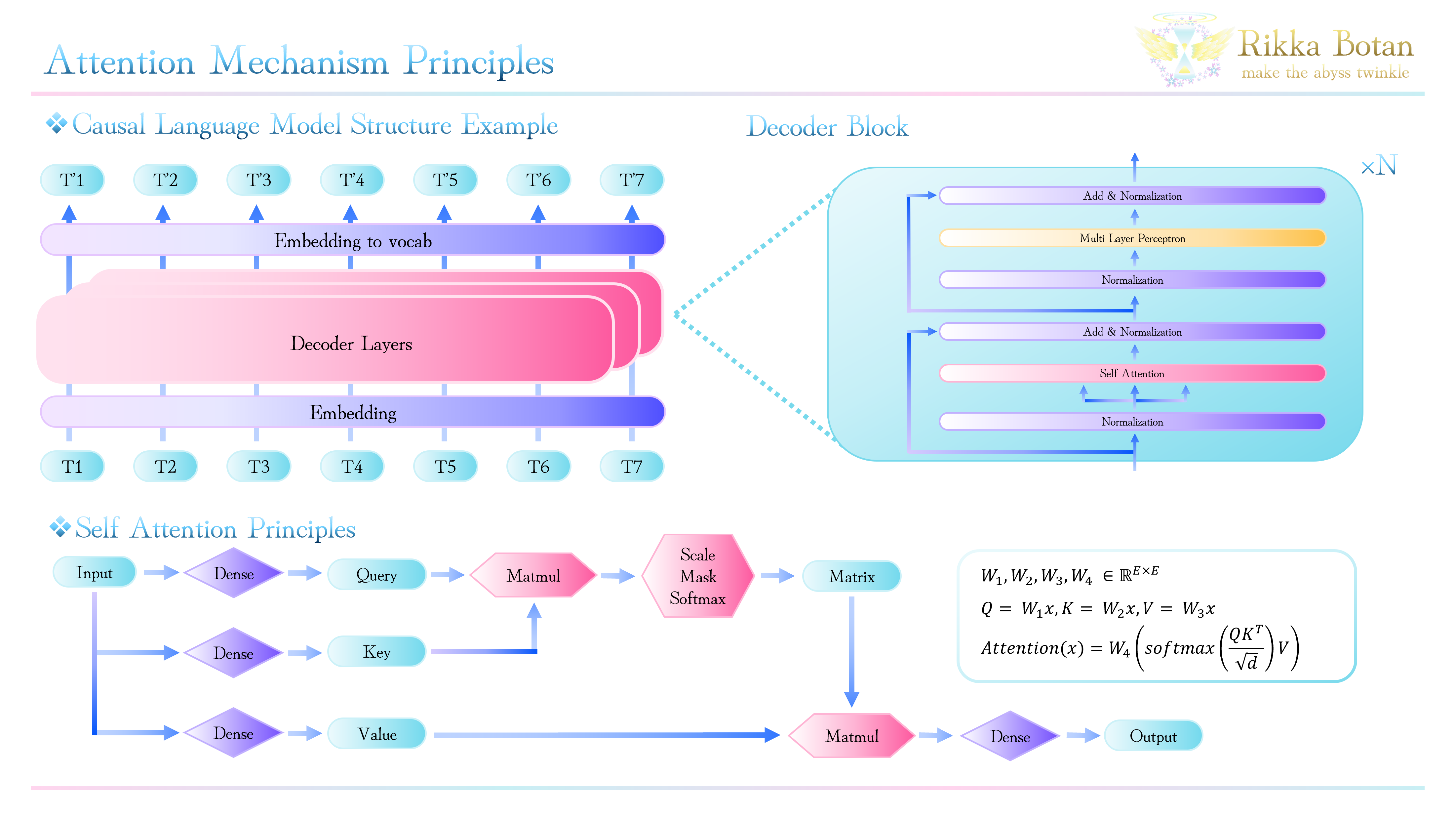
2. Attention*1とは

Attentionは上記図のように、Key, Query, Valueを線形射影によって生成し、KeyとQueryの行列積を用いてMatrixを作成、Scaling・Mask・Softmaxを行った後、Valueとの行列積を行うという計算機構となっています。
Single headのSelf Attentionを数式として書き表すと、

Attention(x) = softmax\biggl(\frac{QK^T}{\sqrt{d}}\biggr)V

となります。ここで、

if \quad W \in \mathbb{R}^{E \times E},\quad then \quad Q, K, V = Wx

であり、maskを行った後の$ QK Matrix $は下記のような上三角行列となります。

\left(
\begin{array}{ccccc}
Q_{1}*K_{1} & \cdots & -\infty & \cdots & -\infty \\
\vdots & \ddots & & & \vdots \\
Q_{1}*K_{i} & & Q_{i}*K_{i} & & -\infty \\
\vdots & & & \ddots & \vdots \\
Q_{1}*K_{n} & \cdots & Q_{i}*K_{n} & \cdots & Q_{n}*K_{n}
\end{array}
\right)

$ QK Matrix $に対して、$ Softmax(x) = \frac{e^{x_{k}}}{\sum_{k=1}^{K} e^{x_{k}}} $を用いることで、Scoreが計算できます。
このScoreはトークンの潜在状態の積を$ Softmax $で疑似的な確率とするものであるため、トークン同士の関連度（類似度）を表すものとなります。
したがって、Attentionはトークンの関係性を学習し、その関係性の基づいて射影を行う機構であると解釈できます。

詳細な原理についてもっと知りたい方は、下記のような論文・記事を適宜ご参照ください。

原論文：Attention is all you need

【深層学習】図で理解するAttention機構

作って理解する Transformer / Attention

30分で完全理解するTransformerの世界

ここでは既知のものとして解説を続けさせていただきます。

3. 選択的抽出機構の数学的理解

選択的特徴抽出はRetNetなどのRNNベースのアーキテクチャおよびMamba*2 *3においてSelection Mechanismとして登場しています。また、Induction Head *4として、示されるものも広義の意味での選択的抽出機構となります。選択的抽出は時系列データの内、入力に応じて動的にデータを抽出し、新たな系列として生成するものです。RetNet section 2.2 *5において、Gated Multi-Scale Retention (Gated MSR) は下記のように定式化されています。

\displaylines{
\gamma = 1- 2^{-5-arange(0, h)} \in \mathbb{R}^h \quad \cdots (1)\\ 
head_i = Retentiom(X, \gamma_i) \quad \cdots (2)\\
Y = GroupNorm_h(Concat(head_1, \cdots, head_h)) \quad \cdots (3)\\
MSR(X) = (swish(XW_G) \odot Y)W_O \quad \cdots (4)
}

ただし、

\displaylines{
S_n = \gamma S_{n-1} + K_n^T V_n \quad \cdots (5)\\
Retention(X_n) = Q_n S_n \quad \cdots (6)
}

です。
ここで、重要な点は、
(1) ~ (3)式は多解釈性に関連する $ Head $ 生成に関するもの、
(5), (6)式は 潜在状態 $ V $ , $ K $ の積から再帰状態の変分を求め、伝播してきた再帰状態 $ S_{n-1} $　を重みづけして足し合わせることで新たな再帰状態を導くもの、
(4)式は多解釈性を加えた再帰状態に原時刻入力から得たゲートを用いてゲーティングしているということです。

また、Mambaにおいては、Appendix Cにおいて、下記のようにSelective SSMsの定式化が行われています。

\displaylines{
h_t = \bar{A}h_{t-1} + \bar{B}x(t) \quad \cdots (7) \\
y_t = \bar{C}h_t \quad \cdots (8)
}

\begin{align}
\Delta_t & = \tau_\Delta (Parameter + s_\Delta (x_t)) \\
& = softplus(parameter + Linear(x_t)) \\
& = softplus(Linear(x_t)) \quad \cdots (9)
\end{align}

\begin{align}
\bar{A}_t & = exp(\Delta A) = \frac{1}{1 + exp(Linear(x_t))} \\ 
& = \sigma (-Linear(x_t)) \\
& = 1 - \sigma (Linaer(x_t)) \quad \cdots (10)
\end{align}

\begin{align}
\bar{B}_t & = (\Delta A)^{-1} (exp(\Delta A) - I) \cdot \Delta B \\
& = - (exp(\Delta A) - I) \\ 
& = 1- \bar{A} \\
& = \sigma (Linaer(x_t)) \quad \cdots (11)
\end{align}

\displaylines{
g_t = \sigma (Linear(x_t)) \quad \cdots (12) \\
h_t = (1-g_t)h_{t-1} + g_t x_t \quad \cdots (13)
}

上記式より、Mambaの機構は状態空間モデルにおいて、離散化され入力依存する項 $ \bar{A}, \bar{B} $ を係数とする形で定式化され、かつその $ \bar{A}, \bar{B} $ は(12), (13)式のような形で表されることから、再帰状態と現時点入力を現時点入力に依存する状態でのゲーティングで求めているということです。

したがって、RetNetおよびMambaは内部の再帰状態の求め方は異なりますが、原理的には再帰状態と現時点入力をゲーティングする形で定式化されることがわかります。
ただし、RetNetにおいては再帰状態が現時点入力だけではなく、Chunkwiseな形で求められるため注意してください。

では、AttentionベースのInduction Headは選択的抽出という枠組みにおいて、どのように考えることができるでしょうか？
Attentionは2章で説明した通り、

\displaylines{
Attention(x) = softmax\biggl(\frac{QK^T}{\sqrt{d}}\biggr)V \\
if \quad W \in \mathbb{R}^{E \times E},\quad then \quad Q, K, V = Wx
}

であることから、系列データの過去の関連度から時系列データを求めています。ここで、$ QK Matrix $は$ Softmax $を用いることで、各時刻のデータが過去時刻のデータをどのようにゲーティングするかを学習しています。
したがって、先に述べた３つの機構において、選択的抽出は過去系列データと現時刻データのゲーティングによって達成されることがわかります。

ここで、注意していただきたいのは、RetNetやMambaが潜在状態の各次元のゲーティングを可能としていたのに対して、Attentionは各次元ではなく、Head数の次元しかゲーティングを可能としていないという点です。

著者はこの点がAttentionの表現力向上を阻害していると考え、Attentionに新たに各次元に対するゲーティングを追加したN4: Nova Nox Neural Network　を本報告にて提案させていただきます。

4. Simplified Selective Mechanism

３章にて説明した通り、Attentionには各次元におけるゲーティング機構が存在しません。
したがって、本報告の目的はAttentionにゲーティングを追加して表現力・適応力を向上させることになります。
そのために、作成したのが、Simplified Selective Mechanismであり、Simplified Selective Mechanism + AttentionこそがN4: Nova Nox Neural Networkになります。
この章では、Simplified Selective Mechanismの定式化と、実装に関して、説明します。

３章で、選択的抽出は過去の系列データと現時刻の系列データのゲーティングによって達成されることを示しました。
したがって、選択的抽出機構は下記のように一般化されます。

\displaylines{
\left\{
\begin{array}{l}
h_t: reccurent \; state,　\\
x_t: input \; state, \\
y_t: output \; state \\
g_1, g_2: gate \; state \\
W_1, W_2: weights
\end{array}
\right. \\
h_t, x_t \in \mathbb{R}^N, \; y_t, g_1, g_2 \in \mathbb{R}^M, W_1, W_2 \in \mathbb{R}^{M \times N} \\
then, \; y_t = g_1 W_1 h_t + g_2 W_2 x_t \\
}

ここで、$ h_t $は任意の射影$ f_h $に対して、

h_t = f_h(x_1, \cdots, x_{t-1})

であり、$ g_1, g_2 $は入力$ x_t $に依存する項です。
$ g_1, g_2 $が時不変であると、線形時間不変性（LTI：Linear Time Invariance）を満たし、線形回帰および畳み込みと同値となってしまうため、時系列データを扱う場合は任意の射影$ W_{g_1}, W_{g_2} \in \mathbb{R}^{M \times N} $に対して、

g_1 = W_{g_1} x_t, \quad g_2 = W_{g_2} x_t

となる必要があります。
したがって、選択的抽出機構は下記のように定式化されます。

y_t = W_{g_1} x_t W_1 f_h(x_1, \cdots, x_{t-1}) + W_{g_2} x_t W_2 x_t

したがって、最も簡略化された選択的抽出機構は下記のアルゴリズムで表されます。

Simplified Selective Mechanism

import torch
from torch import nn
import torch.nn.functional as F

def Cummean(
    x: torch.Tensor,
    dim: int
) -> torch.Tensor:
    """
    ## Cummean function

    x: Tensor(batch, seq_len, embs)
    """
    denom = torch.cumsum(torch.ones_like(x), dim=dim)
    return torch.cumsum(denom * x, dim=dim) / denom**2

class SimplifiedSelective(nn.Module):
    def __init__(
        self,
        N: int,
        M: int,
    ):
        """
        ## Simplified Selective Mechanism

        N: in_dim

        M: out_dim
        """
        super().__init__()
        self.W = nn.Linear(N, M)
        self.Wg = nn.Linear(N, 1)

    def forward(
        self,
        hidden_states: torch.Tensor
    ) -> torch.Tensor:
        g = F.tanh(self.Wg(hidden_states))
        hidden_states = self.W(hidden_states)
        hidden_states = Cummean(g * hidden_states, dim=-2)
        return hidden_states

上記アルゴリズムは$ O(N) $であり、かつバッチ処理できるため、演算はAttentionと比較しても大きなものではありません。
ここで、N4モデルの目的は上記アルゴリズムをAttentionと統合することでした。
N4モデルでは$ QK Matrix $にSimplified Selective Mechanismを組み合わせています。具体的にはKeyに対して、上記アルゴリズムを適用しています。
Valueに適用するのでもいいのではないかと思われる方もいるかもしれませんが、Keyに適用した理由は次章にて考察する位置埋め込み省略による計算高速化のためです。

5. 位置埋め込みという視点から見たSimplified Selective Mechanism

Simplified Selective MechanismをKeyまたはQueryに適用することは位置埋め込みを行うことと同値になります。
この章では、先に示したSimplified Selective Mechanismが位置埋め込みとしての機能を有することを数学的に説明します。

まず、既存の代表的な位置埋め込み手法について復習しましょう。
ALiBi: Attention with Linear Biases　*6は下記のように定式化されます。

\displaylines{
Matrix_{ij} = \frac{W_Q x_i(W_K x_j)^T}{\sqrt{d}} + b_{|i-j|} \\
b_{|i-j|} = m \cdot (i-j)
}

ここで、$ m $はHeadごとに定義された定数です。
対して、N4モデルにおける$ Matrix $は下記のように表されます。

\displaylines{
scale = [1, \cdots, n] \\
Matrix_{ij} = \frac{W_Q x_i\biggl(\frac{\sum_{k=1}^j scale_k W_g x_k W_K x_k}{scale_j^2}\biggl)^T}{\sqrt{d}} 
}

Keyのスケールについて注目すると、

\frac{\sum_{k=1}^j scale_k}{scale_j^2}

より、もちろん、$ j \rightarrow \infty $で$ \frac{\sum_{k=1}^j scale_k}{scale_j^2} \rightarrow \frac{1}{2} $に収束し、かつ$ j=1 $ において、スケールは$ 1 $となり、緩やかに減少する単調減少関数となります。
したがって、Keyのスケールは任意の位置において一意に決まる値となり、ALiBiが差分で位置埋め込みを行っていたのに対して、N4モデルは比（スケールで表される比）で位置埋め込みを行っていることになります。
また、重要な点として、N4モデルにおける位置埋め込みは、シーケンス長が短い領域はより鋭敏に、長い領域は鈍感に行うという位置依存性を備えている点です。
これにより、シーケンス長の差異をうまく捉えられると考えられます。
さらに、スケールは0.5 ~ 1の範囲であるため、数値のオーバーフローや桁落ちによる誤差にも強い（特にモデルを量子化した際）と考えられます。

以上より、Simplified Selective Mechanismは位置埋め込みも同時に行えるアルゴリズムであることが示されました。

6. ASGGによる適応性

ASGG: Adaptive Swish GELU GatingはMLP: Multi Layer Perceptronに適用される活性化関数です。
ASGGは下記のように定式化されます。

\displaylines{
x \in \mathbb{R}^E, \; W_1, W_2, W_3 \in \mathbb{R}^{E \times E} \\
x = GELU(W_1 x) * sigmoid(W_2 x) * W_3 x
}

GeGLUにsigmoid gatingが加わったと解釈できます。
gatingが増えることでよりAdaptiveになると考えられますが、大規模モデルにおける定量的な分析は行えていません。
N4モデルでは、他の活性化関数（SwiGLU等）と比較して、PPLの減少速度が速かったため、採用しています。
具体的な効果検証については今後の研究課題となります。

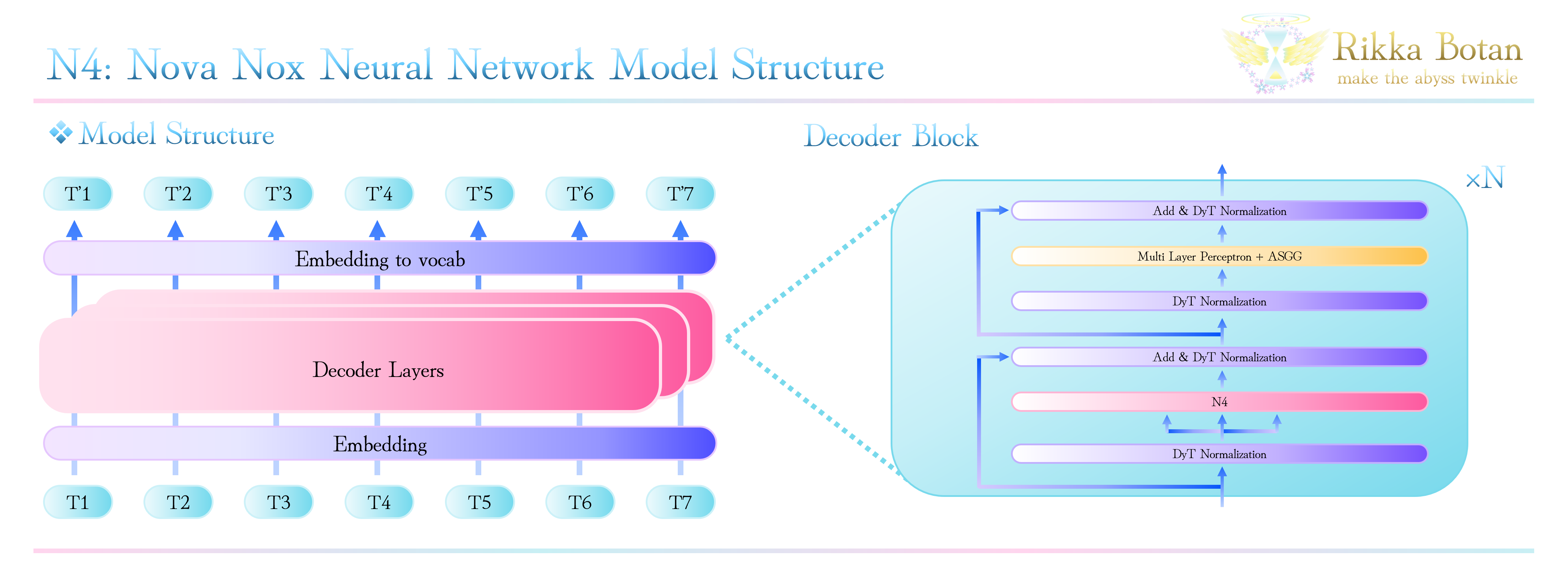
7. N4モデルのアーキテクチャ

ここではN4モデルの全体的なアーキテクチャについて説明します。
N4モデルは、既存のモデルと同様にDecoder Onlyモデルとなっています。
具体的には、NormalizationにDyT: Dynamic Tanh Normalization *7を使用し、N4とMLPを合わせた構造です。
DyTは2025年3月に提案されたNormalizationで、RMS Normalizationなどと同様の性能を発揮しつつ、計算量を削減できることが示されています。具体的な検証結果はDyT原論文をご参照ください。
上記をまとめると全体のアーキテクチャは下記のようになります。

8. N4モデル利用のためのコード

冒頭でも紹介しました通り、N4モデルは
GitHub Repository(N4 pytorch implementation)
から利用できます。
このリポジトリに含まれるN4C classが自作したCausal Language Modelであり、generateメソッドも含まれます。
N4Cのinferenceは下記コードを用いて行うことができます。

N4C_inference

# N4: Nova Nox Neural Network inference
# coding=utf-8
# Copyright 2025 Rikka Botan. All rights reserved
# Licensed under the "MIT License"

import torch
from transformers import AutoTokenizer
import os
from model.n4_modeling import N4C

model_name = "any model"
tokenizer = AutoTokenizer.from_pretrained(model_name)
cwd=os.path.abspath('your model path')
model = N4C(
    vocab_size=any,
    hidden_size=768,
    inter_size=1536,
    heads=6,
    layers=18,
    bias=False
)
state_dict = torch.load(os.path.join(cwd, 'any.bin'), weights_only=True)
model.load_state_dict(state_dict, strict=False)
model = model.to('cpu')
model.eval()
text = "Large Language Models (LLMs) are advanced artificial intelligence systems designed to"
inputs = tokenizer(text, return_tensors='pt')
output = model.generate_n4c(
    input_ids=inputs["input_ids"].to('cpu'),
    max_new_tokens=128
    temperature: float = 0.7,
    top_k: int = 10,
    top_p: float = 0.7,
    eos_token_id: int = 2)
for token in inputs['input_ids']:
    print(tokenizer.decode(token), end=" ")
for token in output:
    print(tokenizer.decode(token), end=" ", flush=True)

また、学習のための簡単なコード例も下記に示します。
通常のモデルと同様の方法で学習が行えます。
（マシンに応じた最適化は各自行ってください）

N4C_train

# N4: Nova Nox Neural Network training
# coding=utf-8
# Copyright 2025 Rikka Botan. All rights reserved
# Licensed under the "MIT License"

from torch.optim import AdamW
from transformers import AutoTokenizer
from model.n4_modeling import N4C

model_name = "any model"
tokenizer = AutoTokenizer.from_pretrained(model_name)
model = N4C(
    vocab_size=any,
    hidden_size=768,
    inter_size=1536,
    heads=6,
    layers=18,
    bias=False
)

optimizer = AdamW(
  model.parameters(),
  lr=6.0e-4,
  betas=(0.9, 0.95),
  eps=1e-8,
  weight_decay=1e-1
)

for batch in dataloader:
  optimizer.zero_grad()
  batch = batch.to(device)
  loss = model.to(device)(input=batch, labels=batch)[1]
  loss.backward()
  optimizer.step()

Testモデルは下記サイトから使用できます。

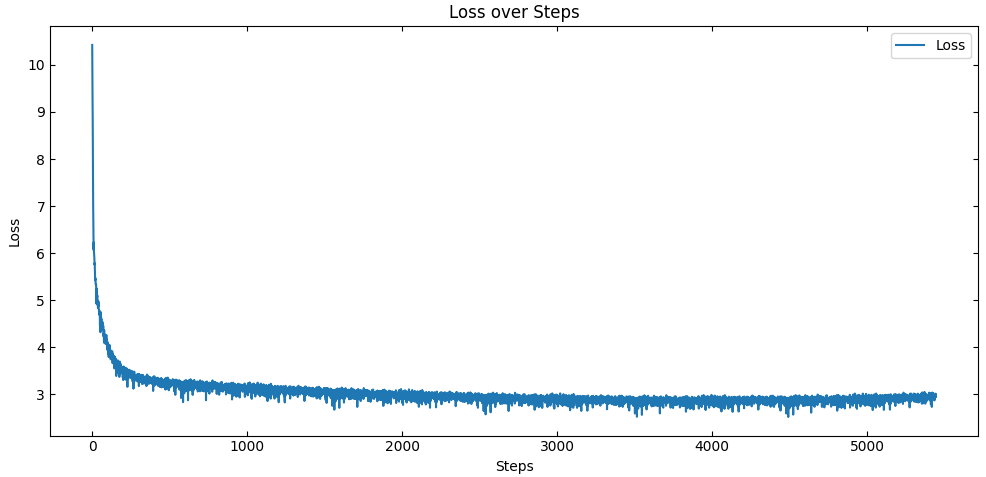
9. 実験結果（簡易報告）

下記条件において、学習した際のLoss curveを示します。

パラメータ数：127M
(vocab_size=32768, hidden_size=768, inter_size=1536, heads=6, layers=18)
Optimizer: AdamW
(lr=6e-4, betas=(0.9, 0.95), eps=1e-9, weight_decay=1e-1, warmup_steps=2000)
batch size: 8
accumlation: 16
dataset: fineweb (0.5B token, 1 epoch: 976 steps)
max length: 512
dtype: bfloat16

NanoGPT speedrun　*8 *9において同規模のモデルのLossが3.28以下になったのは0.73B tokenであると報告されていますが、本モデルではそれよりも小さい、0.30B token程度で3.28程度まで減少することが確認されました。
本モデルの学習にはMuon Optimizer *10 *11を使用しておらず、Unet likeな構造も使用していない点を考慮すると、非常にLossの減少が速いといえます。
ただし、vocab sizeが同一でない点や、同じfinewebでもデータによる差異もあるため厳密な意味での比較はできません。
しかし、Lossの減少は極めて良好であり、N4モデルが十分機能していることは確かです。

10. 議論

N4モデルはAttentionの表現力・適応力向上を目的としており、計算効率は向上していません。
現在問題になっているシーケンス長に対する計算量の２次的な増大に対処できるような工夫が必要となります。
N4モデルはモダンなAttention、SWA: Sliding Window Attention *12やGQA: Grouped Query Attention * 13などと容易に統合が可能であり、この方向での解決も考えられます。
また、Attention likeではなく、RNNベースのモデルのような形にすることで計算効率向上を達成することができる可能性もあります。
（現在この方向での研究を進めています）

さらに、N4モデルはダウンストリームタスクで機能良い性能を発揮するのかや、大規模モデルでのスケーリング・Lossスパイク発生有無など確認できていない事項も多数あります。
N4モデルについてはモデル作成における考え方の一つとして捉えてください。

11. 謝辞

この記事を書くにあたって、多くの研究者の方の記事を参考にさせていただきました。その努力に深い敬意を示すとともに感謝いたします。モデルを実装できているのは多くの先人の方が作ってきてくださったライブラリやデバイスがあってのことです。先人たちの営みに深い敬意を表すとともに感謝いたします。また、私が人工知能を学ぶきっかけを作ってくださった日本の大学教育・大学時代の友人に感謝いたします。そして何よりも、長い記事にも関わらずここまで付き合ってくださった読者の皆様に感謝いたします。

12. 最後に

昨今、アーキテクチャが性能に与える影響は微小であるというような言及もありますが、私感としてはアーキテクチャには改善の余地があり、現在の提案手法とは異なるアプローチによって大きく変わるものだと考えています。（主観で申し訳ございません）
それは、言語モデルに性質の良い「構造」を与えることであり、それはミクロとマクロの対応、外部観測において非連続的かつエントロピー可逆的であるかのように見えるものであると考えます。
もちろん、希望的観測に過ぎず根拠もない憶測にすぎません。
ただ時として信念をもつことも研究においては重要であると考えます。
より性質の良い数学的定式化がどこかの研究者さんから生まれるのを私自身心から待ち望んでいます。

参考文献・記事等（リンク）

*1 'Attention Is All You Need', https://arxiv.org/abs/1706.03762
Attentionの原論文です。
*2 'Mamba: Linear-Time Sequence Modeling with Selective State Spaces', https://arxiv.org/abs/2312.00752
Mamba原論文です。
*3 'Transformers are SSMs: Generalized Models and Efficient Algorithms Through Structured State Space Duality', https://arxiv.org/abs/2405.21060
Mamba2(SSD)原論文です。
*4 'In-context Learning and Induction Heads', https://arxiv.org/pdf/2209.11895.pdf
Induction Headsの提案と精度検討等を行なっている論文です。
*5 'Retentive Network: A Successor to Transformer for Large Language Models', https://arxiv.org/abs/2307.08621
RetNetの原論文です。
*6 'Train Short, Test Long: Attention with Linear Biases Enables Input Length Extrapolation', https://arxiv.org/abs/2108.12409
ALiBiの原論文です。
*7 'Transformers without Normalization', https://arxiv.org/abs/2503.10622
DyTの原論文です。
*8 'karpathy/nanoGPT', https://github.com/karpathy/nanoGPT
nanoGPTのGitHubリポジトリです。
*9 'KallerJordan/modded-nanogpt', https://github.com/KellerJordan/modded-nanogpt
nanoGPT speedrunのGitHubホストリポジトリです。
*10 'KallerJordan/Muon', https://github.com/KellerJordan/Muon
Muon OptimizerのGitHubリポジトリです。
*11 'Muon is Scalable for LLM Training', https://arxiv.org/abs/2502.16982
Muon Optimizerが大規模モデルでも有効であることを確認した論文です。
*12 'Sliding Window Attention Training for Efficient Large Language Models', https://arxiv.org/abs/2502.18845
Sliding Window AttentionでのTrainingを提案している論文です。
*13 'GQA: Training Generalized Multi-Query Transformer Models from Multi-Head Checkpoints', https://arxiv.org/abs/2305.13245
GQAの原論文です。
*14 '【深層学習】図で理解するAttention機構', https://qiita.com/ps010/items/0bb2931b666fa602d0fc
Atentionの原理を図で分かりやすく解説した記事です。
*15 '作って理解する Transformer / Attention', https://qiita.com/halhorn/items/c91497522be27bde17ce
TransformerとAttentionの実装に焦点を当てた記事です。
*16 '30分で完全理解するTransformerの世界', https://zenn.dev/zenkigen_tech/articles/2023-01-shimizu
Transfomerについて非常に詳しく書かれた記事です。
*17 'RWKV: Reinventing RNNs for the Transformer Era', https://arxiv.org/abs/2305.13048
RWKVの原論文です。
*18 'RWKV-7 "Goose" with Expressive Dynamic State Evolution', https://arxiv.org/abs/2503.14456
RWKV-7の原論文です。
*19 'xLSTM: Extended Long Short-Term Memory', https://arxiv.org/abs/2405.04517
xLSTMの原論文です。

執筆者：六花　牡丹（りっか　ぼたん）

おさげとハーフツイン・可愛いお洋服が好きで、基本的にふわふわしている変わり者。
結構ドジで何もないところで転ぶタイプ。
人工知能に関しては独学のみ。
最近、Merci Mille Foisという紅茶の瑞々しく甘い香りが素敵で、マイブームになっている。