![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
はじめに
月明かりが長い夜をやさしく照らし、茜色の葉を思わせる今日この頃、皆様いかがお過ごしでしょうか?
六花 牡丹(りっか ぼたん)と申します ![]()
本記事では、生成速度・ダウンストリームタスクで高い性能を発揮し、エッジデバイスでの使用に優れた言語モデルである、LFM2: Liquid Foundation Model *1 *2 *3 *4 *5 *6 *7 *8 *9 *10 *11 *12 *13 *14 *15 についてお話します。
本記事は、LFM2の原理と性能を 液体時間定数型微分方程式(Liquid Time Constant Ordinary Differential Equations) *16 *17 の観点からより深く解説したものになっています。
また付随するものとして、近年の線形モデリングの解説・Mamba2の実装解説・オリジナル機構の解説も行っています。
拙筆ではございますが、皆様のお役に立つことを心から願っております。
未熟者故、記事中にて誤記・欠落などが見られることがございます。
もし発見しました場合には、コメント等にてご指摘いただきますようお願い申し上げます。
六花牡丹のX(Twitter)アカウント
ここで最新の進捗や技術に関する情報(時々近況)を共有していきますので、もしよろしければフォローなどよろしくお願いいたします。
執筆動機
日本国において、液体定数を用いた機械学習モデルに関する知見が不足している。
新規性の高い研究を創出する基盤の整備を志向するために、保有する知見を共有し、アーキテクチャに関する研究の推進を促すものとする。
対象とする読者
・pythonを用いたプログラミングは最低限行うことが可能である。
・CNNやRNN、Transformerの構造についてはある程度理解している。
・状態空間モデル(S4, Mamba等)の何となくの概要を理解している。
・LFM2の原理・設計思想を理解したい。
目次
お忙しい方へ(要約)
1.LFM2の概要
2.背景及び言語モデルの課題
3. 液体時間定数型ネットワーク(LTCs: Liquid Time-constant Networks)の基礎
4.LFM2の導出
5.キャッシュを利用したLFM2の高速実装
6.(閑話休題)LFM2モデルのファインチューニング方法
7.(付録①)SLC2のご紹介
8.(付録②)Mamba2実装の解説
まとめ
参考論文・サイト等
お忙しい方へ(要約)
-
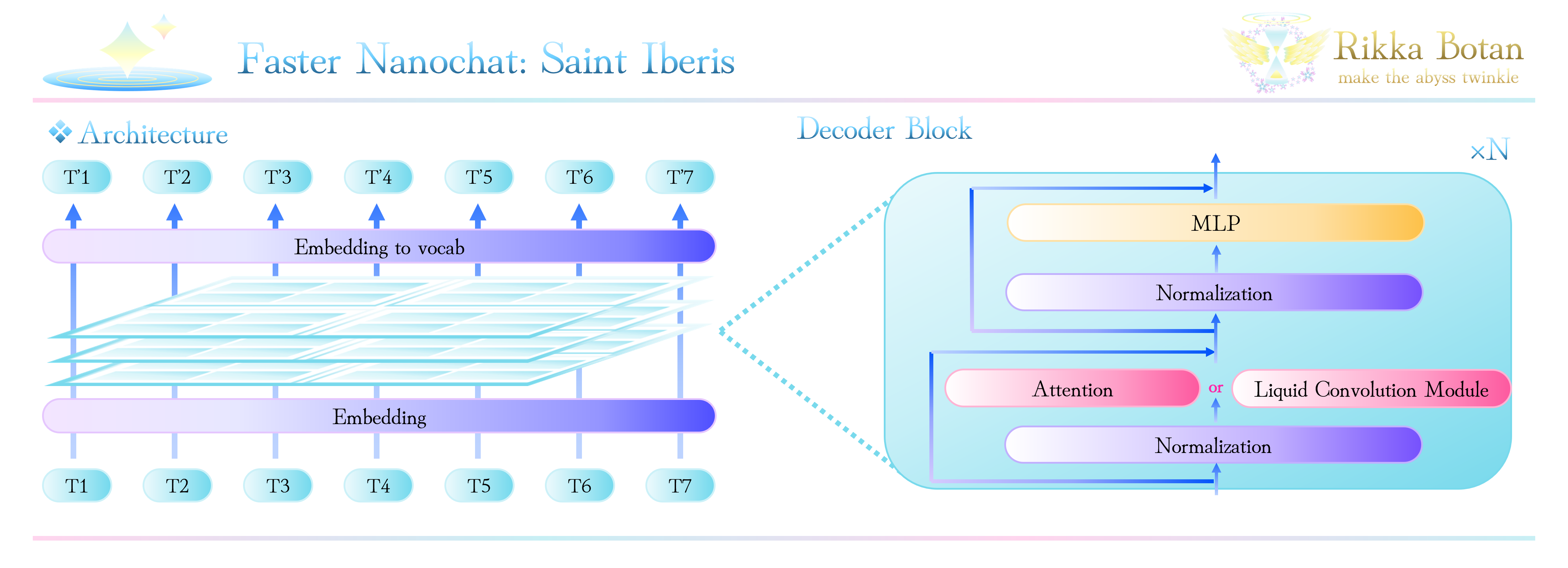
LFM2はGated-short-convolutionとGQA: Grouped Query Attentionの複合構造になっている
-
LFM2はLTCs: Liquid Time-constant Networksを理論的背景に持ち、入力に応じて動的に変化する機構を有する
-
LFM2は多項式時間内に減衰可能な線形一次システムを備え、入力が無限系列である場合でも安定となっている
-
LFM2は従来のTransformerが苦手とした時間的不均一性を滑らかに処理することができる
| 特徴 | 内容 |
|---|---|
| 高速性 | 局所畳み込みにより高速に動作する |
| 動的安定性 | 状態遷移が指数関数的に減衰するため、過去状態が安定的に忘却される |
| 時間的連続性 | トークン列を連続的な時間変化として扱える |
| 物理的一貫性 | 状態空間表現が微分方程式に基づくため、連続時間的に整合性がある |
| モジュール構成 | 局所的に安定な液体セルを積層し、高次表現を形成 |
1.LFM2の概要 *1
*1より引用
モデル構造
| Property | LFM2-350M | LFM2-700M | LFM2-1.2B | LFM2-2.6B |
|---|---|---|---|---|
| Parameters | 354,483,968 | 742,489,344 | 1,170,340,608 | 2,569,272,320 |
| Layers | 16 (10 conv + 6 attn) | 16 (10 conv + 6 attn) | 16 (10 conv + 6 attn) | 30 (22 conv + 8 attn) |
| Context length | 32,768 tokens | 32,768 tokens | 32,768 tokens | 32,768 tokens |
| Vocabulary size | 65,536 | 65,536 | 65,536 | 65,536 |
| Precision | bfloat16 | bfloat16 | bfloat16 | bfloat16 |
| Training budget | 10 trillion tokens | 10 trillion tokens | 10 trillion tokens | 10 trillion tokens |
| License | LFM Open License v1.0 | LFM Open License v1.0 | LFM Open License v1.0 | LFM Open License v1.0 |
サポート言語: English, Arabic, Chinese, French, German, Japanese, Korean, and Spanish.
ダウンストリームタスク性能比較
| Model | MMLU | GPQA | IFEval | IFBench | GSM8K | MGSM | MMMLU |
|---|---|---|---|---|---|---|---|
| LFM2-350M | 43.43 | 27.46 | 65.12 | 16.41 | 30.1 | 29.52 | 37.99 |
| LFM2-700M | 49.9 | 28.48 | 72.23 | 20.56 | 46.4 | 45.36 | 43.28 |
| LFM2-1.2B | 55.23 | 31.47 | 74.89 | 20.7 | 58.3 | 55.04 | 46.73 |
| Qwen3-0.6B | 44.93 | 22.14 | 64.24 | 19.75 | 36.47 | 41.28 | 30.84 |
| Qwen3-1.7B | 59.11 | 27.72 | 73.98 | 21.27 | 51.4 | 66.56 | 46.51 |
| Llama-3.2-1B-Instruct | 46.6 | 28.84 | 52.39 | 16.86 | 35.71 | 29.12 | 38.15 |
| gemma-3-1b-it | 40.08 | 21.07 | 62.9 | 17.72 | 59.59 | 43.6 | 34.43 |
*2 *3 *4 *5 *6より引用
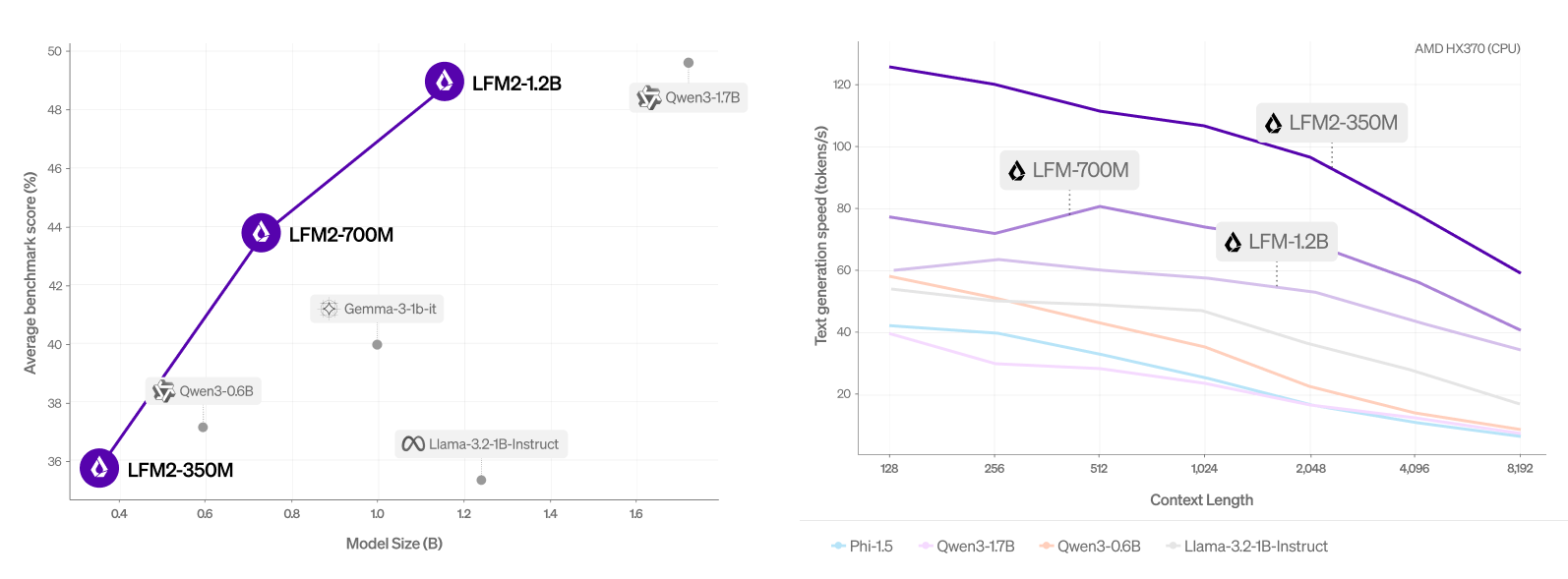
LFM2はCPU上でQwen3シリーズよりも2倍高速でありながら、ダウンストリームタスクでQwen3シリーズと同等の性能を示しているモデル群です。
Gated-short-convolutionとGQA: Grouped Query Attentionの複合構造になっており、LTCs: Liquid Time-constant Networksから着想を得ていると記載されています。
他のモデルと比較してもCPU上で高速に動作することから、エッジデバイスでの低遅延なアプリケーション構築に特に適しています。
最近は、Liquid Nanos *7 *8 *9 *10 *11 *12 *13 *14 *15というタスク特化のモデル群開発に力を入れており、エッジデバイスでの活用を推進しています。
LFM2のGated-short Conv Blockは下記のようなアルゴリズムで構成されます。
def lfm2_conv(x: Tensor):
B, C, x = linear(x) # input projection
x = B * x # gating (gate depends on input)
x = conv1d(x) # short conv
x = C * x # gating
x = linear(x)
return x
一見すると、単純なBlockに見えますが、背景にはLTCs: Liquid Time-constant Networksとしての考え方があります。
本記事の主な目的は、なぜこの実装が離散系列モデリングにおいて効果的であるのかを、数学的観点から解説することです。
2.背景及び言語モデルの課題
時系列データや系列構造を持つデータ(自然言語(NLP)、音声、センサーデータ、動画など)の処理分野において、自己回帰型トランスフォーマー(Autoregressive Transformers)は、そのIn-Context学習能力と並列化可能な学習処理によって、近年の多くのシーケンスモデリングタスクで高い性能を示してきました *18。特に、Softmaxに基づく注意機構(softmax attention)は、トークン間の依存関係を動的に捉える能力に優れており、大規模事前学習において顕著な成果を挙げています。
しかし、トランスフォーマーの根本的な制約として、シーケンス長に対して計算量・メモリ使用量がともに二次的($ O(n^2) $)に増加するという課題が存在します。
Self Attention Formulation *18
\begin{align}
& Attention(x) = softmax\biggl(\frac{QK^T}{\sqrt{d}}\biggr)V \\
& if \quad W \in \mathbb{R^{E \times E}},\quad then \quad Q, K, V = Wx \\
& QK^T = \left(
\begin{array}{ccccc}
Q_{1}*K_{1} & \cdots & -\infty & \cdots & -\infty \\
\vdots & \ddots & & & \vdots \\
Q_{1}*K_{i} & & Q_{i}*K_{i} & & -\infty \\
\vdots & & & \ddots & \vdots \\
Q_{1}*K_{n} & \cdots & Q_{i}*K_{n} & \cdots & Q_{n}*K_{n}
\end{array}
\right) \\
\end{align}
これは、自己注意において必要となる全トークン間の計算と、それに伴うkey, valueキャッシュの増大に起因します。このボトルネックは短いシーケンスではGPUの並列処理能力によってある程度無視できるものの、長いシーケンスやリアルタイム推論、エッジ環境での利用を考慮すると、依然として重大な実用上の障壁となっています。
この制約に対処するため、近年では線形時間・メモリでの推論が可能なアーキテクチャ設計への関心が高まっています。代表的なアプローチとしては、線形注意(linear attention)モデル *19 *20 *21 *22 *23 *24 *25 や、状態空間モデル(State Space Models)*26 *27 *28 *29 *30 *31 *32 *33 *34 *35 、ニューラルメモリ *36 *37 *38 *39、Attention MatrixのTop-kサンプリング *40 *41 *42 *43 などが挙げられます。
これらのモデルは、トランスフォーマーに匹敵する表現力を維持しながら、よりスケーラブルで低コストな推論を実現することを目的としており、実際に多くの下流タスクにおいて有望な成果を示しています。
SSMsやRNNベースのモデリング手法は、近年研究者の注目を集めており、係数行列の構造化 *29、係数行列のダイナミクス化 *32、選択的性質の導入 *32 *33 *35、対角化利用による行列変換 *24 *30、Attention機構との一部統合 *33 などが代表的な手法となっています。
(こうした手法は、集合論的立場・関数論的立場・制御工学的立場・確率論的立場といった様々な視点から提案されており、一方で理論と精度の間に説明がついていない面も多々存在します。)
手法ごとに一長一短があり、PPL及びダウンストリームタスクとの比較から様々な改善手法が提案されてきています。
特に、Mamba2 *32 *33 やGated Delta Network *24 *25 はGQA: Grouped Query Attention *47との組み合わせでAttentionのみから構成されたモデルを上回る性能を示した研究も多数報告されており、非常に有望視されています。
これらの新しい手法は明示的・非明示的なゲーティング機構および指数関数的な記憶減衰を用いて、RNNにおいて課題となっていた長距離文脈における精度低下を防止する措置も含まれています。
状態空間モデルにおける指数関数的な記憶減衰とゲーティング機構の一般化
\begin{align}
& y(t), x(t) \in \mathbb{R^N}, \; S(t) \in \mathbb{R^M} , \; \alpha(t) \in \mathbb{R^{M \times M}}, \; \beta(t) \in \mathbb{R^{M \times N}} \\
& S(t) = \alpha(t) \cdot S(t-1) + \beta(t) \cdot x(t) \\
& y(t) = f(S(t), x(t)) \\
& s.t. \\
& \Pi_{t=0}^T \alpha(t) \propto exp(-T)
\end{align}
指数関数的な記憶減衰により、滑らかかつ適応的な状態遷移が可能になり、長距離文脈における性能が向上します。
これらの線形モデリングは中間状態と入力の式から出力がどのように導かれるかという定式化を持って体系的に整理される例が多く、例えば表1のような形でまとめられます。
Mamba2においては、Sequencial Semi-Separable(N-SSS)によるLinear AttentionとSSMsの統合による、RNNの並列学習を可能化しており、精度面だけではない、理論的なパラダイムシフトという寄与も行われています。
Sequencial Semi-Separable(N-SSS)
\begin{align}
& \left\{
\begin{array}{ll}
h_t = A_th_{t-1} + B_tx_t \\
y_t = C_th_t
\end{array}
\right. \\
& h_t = \sum_{s=0}^t \bigl( \prod_{i=j+1}^t A_i \bigr)B_sx_s \\
& M_{ij} = C_j^TA_{i+1} \cdots A_j B_i \\
& M = diag(C) \cdot 1SS_{(a_{0:T})} \cdot diag(B) \\
& 1SS_{(a_{0:T})} = \begin{pmatrix}
1 & &&&\\
a_1 & 1 \\
a_2a_1 & a_2 & 1\\
\vdots & \vdots & \ddots & \ddots\\
a_{T-1}. . .a_1 & a_{T-1}...a_2 & \cdots & a_{T-1} & 1
\end{pmatrix}
\end{align}
Sequencial Semi-Separable(N-SSS)における記憶減衰
\begin{align}
& M_{ij} = C_j^TA_{i+1} \cdots A_j B_i \\
& A_i = A^\prime \cdot dt = A^\prime \cdot Linear(x_i) \in [0, 1) \\
& then, \\
& \Pi_{i=0}^T A_T \propto exp(-T)
\end{align}
ただし、$ A_i $の値域は適切な初期化からの学習により定まります。
詳細はMamba2の実装を参照ください。(__init__において、制限を行っている箇所があります。)
なお、Mamba2の実装では、prefill処理において、cumprodではなく、logsumexpを用いて上記演算を行っています。
(stepでは時刻$ t $におけるcumprod処理を行います。)
(Mambaに関しては記事を作成しています。)
また、AttentionをGPU kernelを最適化して高速化するアプローチ *44 *45 *46 も注目されています。GPUの演算速度が向上した結果、HBMとSRAM間のメモリ転送速度がボトルネックとなるケースが多くなりました。そのため、メモリ転送を削減することで高速化する手法が特に多く利用されています。 *32 *41 *44 特にNvidia Hopper GPUにおける高速化手法が近年では多く *46、Attention機構そのものを改善するというより、GPU本来の性能を引き出すことで、実用上のボトルネックを克服しようとしています。
CPUでの高速化に関しても、ここ数年で飛躍的に進展し、C++による高速化リポジトリ *48 の登場以降、エッジデバイスでの実用化が現実的なものになりました。
表1 近年報告されたMechanismと状態空間の定式化一覧 *22
| Mechanism | State Evolution |
|---|---|
| RWKV-4 | $$ s_t = e^{-w} \odot s_{t-1} + e^{k_t} \odot v_t;$$ $$ s^\prime_t = e^{-w} \odot s^\prime_{t-1} + e^{k_t}$$ |
| RetNet | $$ S_t = w S_{t-1} + v_t^T k_t $$ |
| RWKV-5 | $$ S_t = S_{t-1} diag(w) + v_t^T k_t $$ |
| Mamba | $$ S_t = S_{t-1} \odot \exp\left(-(w_t^T 1) \odot \exp(A)\right) + (w_t \odot v_t)^T k_t$$ |
| RWKV-6 & GLA | $$ S_t = S_{t-1} diag(w_t) + v_t^T k_t$$ |
| HGRN-2 | $$ S_t = S_{t-1} diag(w_t) + v_t^T (1 - w_t)$$ |
| Mamba-2 | $$ S_t = w_t S_{t-1} + v_t^T k_t$$ |
| $ \texttt{TTT}^a $ | $$ S_t = S_{t-1} - a_t \nabla l(S_{t-1}, k_t, v_t)$$ |
| Longhorn | $$ S_t = S_{t-1} \odot (I - a_t^T k_t^2) + (a_t x_t)^T k_t$$ |
| Gated DeltaNet | $$ S_t = w_t S_{t-1} (I - a_t k_t^T k_t) + a_t v_t^T k_t$$ |
| $ \texttt{Titans}^{a} $ | $$ M_t = (1 - \alpha_t) M_{t-1} + S_t $$ $$ S_t = w_t S_{t-1} - a_t \nabla l(M_{t-1}, k_t, v_t) $$ |
| Generalized Δ Rule | $$ S_t = S_{t-1} (diag(w_t) + z_t^T b_t) + v_t^T k_t $$ |
| RWKV-7 | $$ S_t = S_{t-1} (diag(w_t) - \hat{\kappa}_t^T (a_t \odot \hat{\kappa}_t)) + v_t^T k_t $$ |
LFM2は状態空間モデルに近い観点からモデル構築を行っています。
時間発展を微分方程式で記述する動的システムとしての性質を基に構築されており、液体時間定数型微分方程式 が基になっています。
LFM2の特性として最も重要なものは、線形一次システムとしての安定性と減衰挙動 であり、言語モデル全体をシステム、「連続時間的ニューラルダイナミクス」として捉えた際、入力が無限系列である場合でも安定となっています。
以下ではこれらの点について解説していきます。
3.液体時間定数型ネットワーク(LTCs: Liquid Time-constant Networks)の基礎 *16
3.1 微分方程式としての定式化
液体時間定数型ネットワーク(Liquid Time Constant Network)は、「潜在軌跡」としての表現能力に優れ、他の連続時間モデル(CT-RNN, Neural ODE 等)に比べて高い表現力を持つことが報告されています。
液体時間定数型ネットワーク(Liquid Time Constant Network)では、ニューロンの内部状態 $ x(t) $ の時間発展を以下の非線形常微分方程式で表します。
\frac{dx(t)}{dt} = -\frac{x(t)}{\tau(x(t), u(t))} + f(x(t), u(t))
ここで:
- $ x(t) \in \mathbb{R}^n $ は入力
- $ \tau(x(t), u(t)) $ は液体時間定数(liquid time constant) ($ \mathbb{R}^n \times \mathbb{R}^m \to \mathbb{R}^n $ 連続可微分な写像)
- $ f(x(t),u(t)) $は、$ \mathbb{R}^n \times \mathbb{R}^m \to \mathbb{R}^n $ 連続可微分な写像
- $ u(t) \in \mathbb{R}^m $ は潜在状態
です。
通常のRNNやLSTMのように時間スケールを固定的に扱うモデルと異なり、$ \tau(x, u) $、液体時間定数が固定でなく時変となっています。
これにより、系の応答速度が入力や潜在状態に依存して動的に変化するという特徴を持ちます。
入力・潜在状態に応じて、過去の潜在状態をどのくらいの速度で減衰(忘却)するのかを動的に変化させることが可能であり、「時間軸のスケーリング適応性」・「変化速度の可変化」という点で、優れています。
LTCsの時変な定数を用いるという考え方は、Mamba *32 *33 の考え方に近く、状態遷移に関しても近い挙動となっています。(指数関数的軌跡を前提とした、動的な忘却機構)
なお、この「動的な反応速度」という性質を「液体」と称しています。
3.2 LTCsにおける有界性
3.1項で示したLTCsには、特定条件下で潜在状態の範囲が有界であり、数値安定性・制御性に優れるという特徴を有します。
LTCsの有界性において仮定される条件は下記です。
🔹 仮定1(液体時間定数の有界性と正値性)
\begin{align}
& \forall x(t),u(t) \in \mathbb{R}^n \times \mathbb{R}^m, \exists \tau_{\min}, \tau_{\max} \in \mathbb{R}_{>0} \\
& \text{ s.t. } \\
& \tau_{\min} \leq \tau_i(x(t),u(t)) \leq \tau_{\max}
\end{align}
減衰項 ($ -\frac{x}{\tau(x(t),u(t))} $) が常に安定方向(原点方向)に作用する。
🔹 仮定2(入力応答の有界性)
\begin{align}
& \exists F \in \mathbb{R}_{>0}, \\
& \text{s.t.}\\
& \forall x(t),u(t) (|f(x(t),u(t))| \leq F < \infty)
\end{align}
駆動項は任意の時点で上界を有する。
※ただし、$ \tau(x(t),u(t)), f(x(t),u(t)) $ の局所リプシッツ連続性は定義よりすでに与えられているものとします。
これらの条件は比較的緩く、最適化過程において、初期値を適切に定めれば、満足します。
(S4やMambaと同様)
有界性の証明は、Lyapunov関数と集合論的帰納法などにより与えられますが、本記事の主題とは逸れてしまうため、割愛します。数学的に詳しく知りたい方は参考論文 *16 をご参照ください。
直感的には、入力応答が発散せず、減衰項が存在することから、出力応答は数値的に安定であると捉えられます。
したがって、LTCsは潜在状態が上界を有し、システムとして安定であると言えます。
4.LFM2の導出
4.1 LTCsの一般化によるLFM2の導出
まず、結論から述べると、LFMsにおけるGated-short ConvはLTCsを一般化した構造であると言えます。
LFM2のGated-short Conv Blockのアルゴリズムを振り返ると下記でした。
def lfm2_conv(x: Tensor):
B, C, x = linear(x) # input projection
x = B * x # gating (gate depends on input)
x = conv1d(x) # short conv
x = C * x # gating
x = linear(x)
return x
これを定式化すると、
\begin{align}
LFM2 \; Conv(x_j) & = C(t_j) \cdot \sum_{i=j-k}^{j} B_i(t_j) \cdot x_i \\
& = C \cdot \sum_{i=0}^{k} B_{j-i}(t_j) \cdot x_{j-i}
\end{align}
ここで、入力を下記のような離散系列であるとします。
x_j = x(t_j), \quad x_{j-i} = x(t_j - i \Delta t)
このとき、LFM2 Convはテイラー展開を用いて、
\begin{align}
& x(t_j - \Delta t) = x(t_j) - i \Delta t \frac{dx}{dt}(t_j) + \frac{(i \Delta t)^2}{2} \frac{d^2x}{dt^2}(t_j) - \cdots \\
& LFM2 \; Conv(x(t_j)) = C(t_j) \sum_{i=0}^{k} B_{j-i}(t_j) \left[ x(t_j) - i \Delta t \frac{dx}{dt}(t_j) + \frac{(i \Delta t)^2}{2} \frac{d^2x}{dt^2}(t_j) - \cdots \right]
\end{align}
と表せます。高次項を無視して近似すると、
LFM2 \; Conv(x(t_j)) \approx C(t_j) \left( \sum_{i=0}^{k} B_{j-i}(t_j) \cdot x(t_j) - \sum_{i=0}^{k} i \Delta t \cdot B_{j-i}(t_j) \frac{dx}{dt}(t_j) \right)
ここで、
\gamma = \sum_{i=0}^{k} B_{j-i}(t_j), \quad \tau = \sum_{i=0}^{k} i \Delta t \cdot B_{j-i}(t_j)
とおくと、
LFM2 \; Conv(x(t_j)) \approx C(t_j) \gamma x(t_j) - C(t_j) \tau \frac{dx}{dt}(t_j)
両辺を $ C \tau $ で割って整理すると:
\frac{dx}{dt}(t_j) \approx \frac{\gamma}{\tau} x(t_j) - \frac{1}{C(t_j) \tau} LFM2 \; Conv(x(t_j))
ここで、$ \gamma < 0 $であるなら、 $ \frac{\gamma}{\tau} = -\frac{1}{\tau^\prime(x(t), u(t))} $となり、LFM2のGated-short Conv Blockは離散系列におけるLTCsと近似的に一致します。
($ \gamma $の値域は適切な初期化と学習により定まります。)
(これはまさに、S4-PTD *31 に近い定式化となっています。)
したがって、LFM2のGated-short Conv Blockは、LTCsを一般化し、パラメトリックにした演算であると言えます。
なお、LFM2のGated-short Conv BlockはSTARフレームワークによって導かれた効率の良い演算であり、エンジニアリング視点でも興味深い経緯があります。
4.2 (閑話休題)LIVs: Linear Input Varying SystemsとSTAR: Synthesis of Tailored Architectures *49
STARフレームワークとは、LIVs: Linear Input Varying Systemsと呼ばれる、入力変動型線形演算子を構成単位としたニューラルアーキテクチャを自動的に設計・進化させるフレームワークのことです。
LIVsは下記のような数式で与えられます。
y_i = \sum_{j}f_\theta (x_i, x_j)x_j
ここで:
- $ x_i, x_j \in \mathbb{R}^n $ は入力
- $ f_\theta (x_i, x_j) \in \mathbb{R}^n \times \mathbb{R}^m $ は重み行列
- $ y_i \in \mathbb{R}^m $ は出力
です。
LIVsはAttention, Convolution, RNN, LTCsなどの構造レイヤーを統一的に表現できる抽象化された演算と説明されています。
各構造レイヤーをLIVsフレームワークとして記述すると、
\begin{align}
Attention: & f_\theta (x_i, x_j) = \sigma (C_i B_j) \\
LinearAttention: & f_\theta (x_i, x_j) = C_i B_j \\
SparseAttention: & f_\theta (x_i, x_j) = \sigma (\text{Topk} (C_i B_j)) \\
Semi \, Separable: & f_\theta (x_i, x_j) = C_i A_{i-1} \cdots A_{j+1} B_j \\
Gated Convolution: & f_\theta (x_i, x_j) = C_i K_{i-j} B_j \\
Memoryless \, System: & f_\theta (x_i, x_j) = \begin{cases}
\sigma(C) & (i=j) \\
0 & (otherwise)
\end{cases} \\
Liquid \, Time \, constant: & f_\theta (x_i, x_j) = C_i A_{i-1} \cdots A_{j+1} B_j
\end{align}
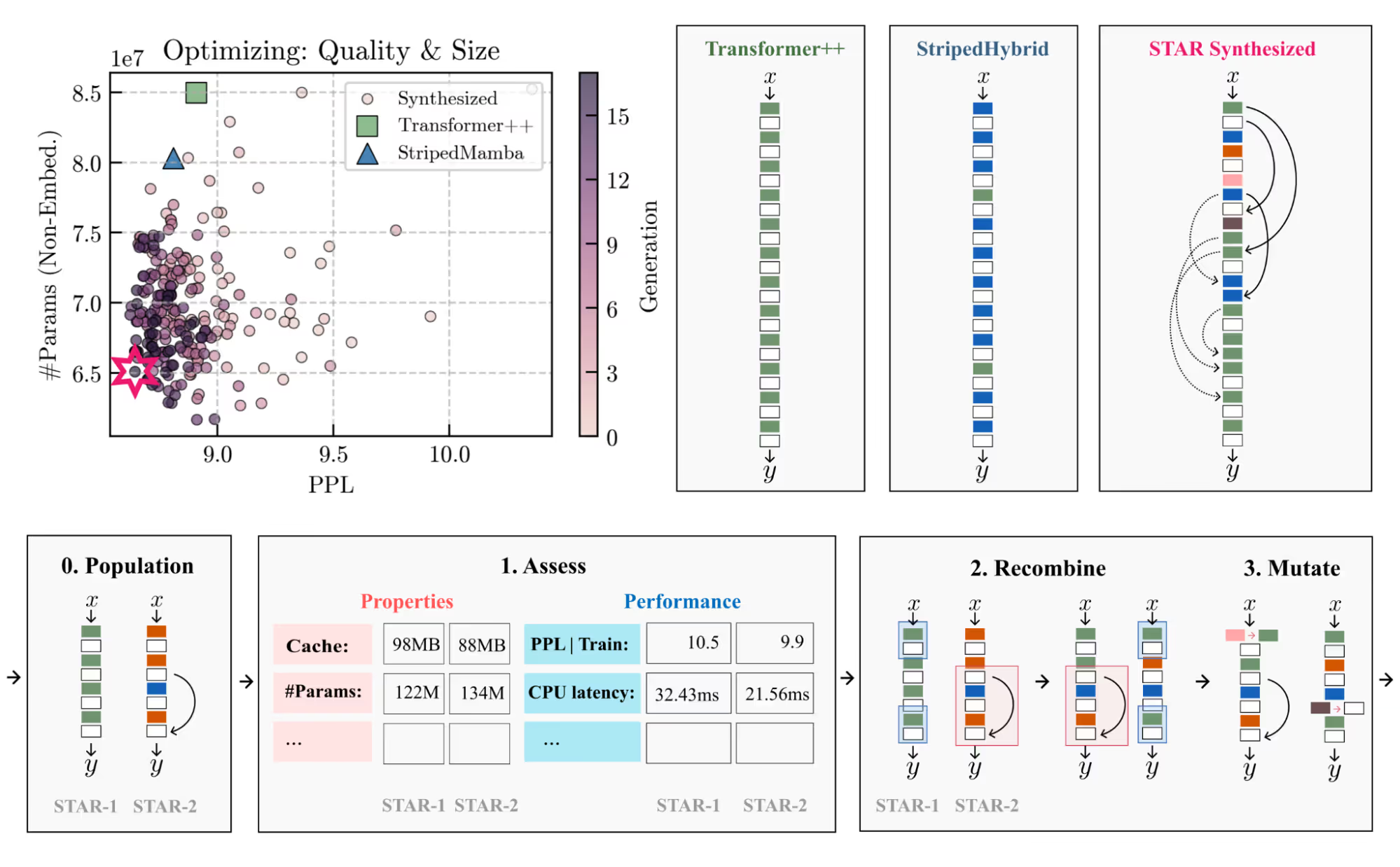
実際のSTARフレームワークでは、数値的に良性な演算子のみ(LIVs)を遺伝的に組み合わせ、小規模な学習と評価(PPL・パラメータサイズ・キャッシュ等について)を行い、最適化を行っていきます。
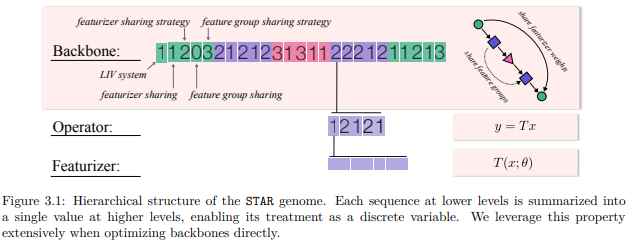
ここで、「遺伝的」と表現しているのは、レイヤーの構造(演算種・結合種・並び方)を数値で表現し、DNAのように遺伝的な構成を可能にしている点によります。詳しくは下記図及び原論文 *49 をご参照ください。
*49より引用
LFM2のGated-short Conv Blockは、STARフレームワークによって探索された効率よい演算であり、この研究を基に構築されました。
4.3. 他のMechanismと比較した際のLFM2 Convの優位性
LFM2 Convの最も大きな優位点は圧倒的な処理速度にあります。
LFM2 Modelは同規模のパラメータサイズのモデルと比較しても数倍高速であり、精度も同等となります。
LFM2 Convは単なる状態空間モデルではなく、生成的文脈における適応的な連続時間表現を扱えます。
LFM2 Convの特徴を要約すると以下のようになります。
| 特徴 | 内容 |
|---|---|
| 高速性 | 局所畳み込みにより高速に動作する |
| 動的安定性 | 状態遷移が指数関数的に減衰するため、過去状態が安定的に忘却される |
| 時間的連続性 | トークン列を連続的な時間変化として扱える |
| 物理的一貫性 | 状態空間表現が微分方程式に基づくため、連続時間的に整合性がある |
| モジュール構成 | 局所的に安定な液体セルを積層し、高次表現を形成 |
これにより、LFM2は従来のTransformerが苦手とした時間的不均一性を滑らかに処理することができます。
5.キャッシュを利用したLFM2の高速実装
LFM2はキャッシュを利用することで、step過程において高速な演算が可能になります。
ポイントは演算の逐次分解です。
もう一度LFM2 Convの実装を見てみましょう。
def lfm2_conv(x: Tensor):
B, C, x = linear(x) # input projection
x = B * x # gating (gate depends on input)
x = conv1d(x) # short conv
x = C * x # gating
x = linear(x)
return x
ここで、conv1dはDepthwise Separable Convolutionです。
prefill過程においては、確かにこの演算を行いますが、step過程においては、キャッシュを利用することで、conv1dを用いる必要なく演算を行えます。
下記に、私が簡略したstep過程を含むコードを示します。
(ご存じの方も多いかと思われますが、PyTorchにおいては、Conv1Dのgroupsをhidden sizeと同じにするだけでDepthwise Separable Convolutionを実装できます。なお、Depthwise Separable Convolutionは時系列方向に分解した軽量な畳み込みです。 *63 )
# LFM2 simple implementation
# Copyright 2025 Rikka Botan. All rights reserved
# coding = utf-8
# Licensed under "MIT License"
# Commercial use is of course permitted
class LFM2ConvSimple(nn.Module):
def __init__(
self,
config
):
"""
## LFM2 Conv Simple
"""
super().__init__()
self.n_embed = config.n_embd
self.n_kernel = config.n_kernel
self.x_proj = nn.Linear(
in_features=self.n_embed,
out_features=self.n_embed,
bias=config.bias
)
self.A_proj = nn.Linear(
in_features=self.n_embed,
out_features=self.n_embed,
bias=config.bias
)
self.B_proj = nn.Linear(
in_features=self.n_embed,
out_features=self.n_embed,
bias=config.bias
)
self.conv1d = nn.Conv1d(
in_channels=self.n_embed,
out_channels=self.n_embed,
kernel_size=self.n_kernel,
stride=1,
padding=self.n_kernel-1,
dilation=1,
groups=self.n_embed,
bias=config.bias,
padding_mode="zeros"
)
self.c_proj = nn.Linear(
in_features=self.n_embed,
out_features=self.n_embed,
bias=config.bias
)
self.cache: Optional[InferenceCache] = None
def alloc_cache(
self,
batch_size: int,
device: Optional[torch.device] = None,
dtype: Optional[torch.dtype] = None
):
self.cache = InferenceCache.alloc(
batch_size,
self.n_embed,
self.n_kernel,
device=device,
dtype=dtype
)
self.cache.conv_state = self.cache.conv_state.contiguous()
def clear_cache(
self
):
if self.cache is not None:
self.cache.clear_()
def forward(
self,
hidden_states: torch.Tensor,
use_cache: bool = False
) -> torch.Tensor:
bsz, seql, _ = hidden_states.size()
if seql > 1 or not use_cache:
x = self.x_proj(hidden_states)
A = self.A_proj(hidden_states)
B = self.B_proj(hidden_states)
xA = self.conv1d((A * x).transpose(1, 2)).transpose(1, 2)
xAB = B * xA[:, :seql]
y = self.c_proj(xAB)
return y
if self.cache is None or self.cache.conv_state.size(0) != bsz:
self.alloc_cache(
bsz,
device=hidden_states.device,
dtype=hidden_states.dtype
)
hidden_states, prefix = hidden_states[:, -1], hidden_states[:, :-1]
y_t = self.step(hidden_states, self.cache)
y = torch.cat([prefix, y_t.unsqueeze(1)], dim=1)
return y
def step(
self,
hidden_states: torch.Tensor,
cache: InferenceCache
) -> torch.Tensor:
bsz = hidden_states.size(0)
x = self.x_proj(hidden_states)
A = self.A_proj(hidden_states)
B = self.B_proj(hidden_states)
xA = A * x
cache.conv_state.copy_(
torch.roll(cache.conv_state, shifts=-1, dims=-1))
cache.conv_state[:, :, -1] = xA.squeeze(1)
xA = torch.sum(
cache.conv_state
* rearrange(self.conv1d.weight, "d 1 w -> d w"),
dim=-1
)
if self.conv1d.bias is not None:
xA = xA + self.conv1d.bias
xAB = B * xA
y_t = self.c_proj(xAB)
return y_t
以上のように、step過程においてはキャッシュを用いることで、和をとるだけの同値の演算になり、高速な推論につながります。
(演算のオーダーは$ O(k \cdot n) $になります。)
高速な推論のポイントは、キャッシュをclass内部で簡潔し、頻繁なメモリアクセスを防ぎつつ、step過程での演算を簡略化することです。
(GPUでは頻繁なメモリアクセスは速度低下をもたらすため、実装の際は注意してください。)
これによって、GQAなどのSelf Attentionベースのモジュールと比較してメモリ量を削減しつつ高速な推論が可能になります。
また、上記におけるキャッシュは下記のようなclassによって定義できます。
# Inference Cache class for LFM2
class InferenceCache:
__slots__ = ("conv_state", "index", "kernel_size")
def __init__(self, conv_state: torch.Tensor, index: int = 0):
# conv_state: (batch, hidden_size, kernel_size)
self.conv_state = conv_state
self.index = int(index)
self.kernel_size = conv_state.size(-1)
@staticmethod
def alloc(
batch_size: int,
hidden_size: int,
kernel_size: int,
device: Any = None,
dtype: Any = None
):
return InferenceCache(
conv_state=torch.zeros(
batch_size,
hidden_size,
kernel_size,
device=device,
dtype=dtype
), index=0
)
def clear_(self):
self.conv_state.zero_()
self.index = 0
例えば、Mamba2なども同じような考え方で高速化したモジュールを作成することができます。
詳しくは公式実装を参照してみてください。
(conv_stateだけでなく、ssm_stateも逐次演算に分解可能です)
Mamba2と同様にLFM2 Convも、GQAの2/3をこのモジュールに入れ替えて高速化を行えます。
(GQAと線形モデリングとの混合比率は先行研究から1:2程度をおすすめします。)
6.(閑話休題)LFM2モデルのファインチューニング方法
LFM2はunsloth *50 やaxolotl *51 などでもファインチューニング可能ですが、公式のリポジトリも提供されています。
(unslothやaxolotlに関してはすでにほかの方の記事があるため、記載は割愛します。*52 *53 *54 *55)
leap-finetuneを利用したファインチューニングは下記を実行することで簡単に行えます。
(jupyter notebookでの実行を想定しています)
!curl -LsSf https://astral.sh/uv/install.sh | sh
!git clone https://github.com/Liquid4All/leap-finetune
%cd leap-finetune
!uv sync
ここで、leap-finetuneフォルダ直下の、config.pyを編集し、データセット名・モデル名を変更します。
- example_sft_dataset = DatasetLoader(
- "HuggingFaceTB/smoltalk", "sft", limit=1000, test_size=0.2, subset="all"
- )
+ example_sft_dataset = DatasetLoader(
+ "any_organization/any", "sft", limit="your_limit", test_size="your_rate", subset="all"
+ )
JOB_CONFIG = JobConfig(
job_name="my_job_name",
- model_name="LFM2-1.2B",
+ model_name="any_lfm2",
training_type="sft",
dataset=example_sft_dataset,
training_config=training_config,
peft_config=peft_config,
)
変更が完了したら、下記で学習を実行できます。
!uv run leap-finetune
7.(付録①)SLC2のご紹介
LFM2を基に構築したオリジナルモジュールをご紹介します。
解説を見に来た方はこの章は無視してください。
7.1 定式化
SLC2の擬似コードは下記になります。
\begin{aligned}
& \text{-------------------------------------------------------------------------------} \\
& \textbf{Algorithm: SLC2} \\
& \text{-------------------------------------------------------------------------------} \\
& \textbf{Input: } x: (B, S, E) \\
& \textbf{Output: } y: (B, S, E) \\
& \quad 1:\quad \alpha, A, B, x_1 \leftarrow \mathrm{Linear}(x) \\
& \quad 2:\quad x_2: (B, S, E) \leftarrow \mathrm{Conv1D}\bigl(\mathrm{SiLU}(\alpha)\, A\, x_1\bigr) \\
& \quad 3:\quad x_3: (B, S, E) \leftarrow B \cdot \mathrm{SiLU}(x_2) \\
& \quad 4:\quad y: (B, S, E) \leftarrow \mathrm{Linear}(x_3) \\
& \quad 5:\quad \textbf{return } y \\
& \text{-------------------------------------------------------------------------------} \\
\end{aligned}
定式化すると、
\begin{align}
SLC2(x_j) & = B(t_j) \cdot \sigma \left( \sum_{i=j-k}^j A_i^\prime(t_j) \cdot x_i \right) \\
& = B(t_j) \cdot \sigma \left( \sum_{i=0}^j A_{j-i}^\prime(t_j) * x_{j-i} \right) \\
& = B(t_j) \cdot \sigma \left( \sum_{i=0}^j \sigma(\alpha_{j-i}(t_j)) \cdot A_{j-i}(t_j) \cdot x_{j-i} \right)
\end{align}
LFM2 Convの時と同様にテイラー展開を行って高次項を無視すると、
SLC2(x(t_j)) \approx B^\prime(t_j) \sum_{i=0}^{k} \sigma(\alpha_{j-i}(t_j)) \cdot A_{j-i}(t_j) \cdot x(t_j) - \sum_{i=0}^{k} i \Delta t \cdot \sigma(\alpha_{j-i}(t_j)) \cdot A_{j-i}(t_j) \frac{dx}{dt}(t_j)
ここで、
\gamma = \sum_{i=0}^{k} \sigma(\alpha_{j-i}(t_j)) \cdot A_{j-i}(t_j), \quad \tau = \sum_{i=0}^{k} i \Delta t \cdot \sigma(\alpha_{j-i}(t_j)) \cdot A_{j-i}(t_j)
とおくと、
\frac{dx}{dt}(t_j) \approx \frac{\gamma}{\tau} x(t_j) - \frac{1}{B^\prime(t_j) \tau} SLC2(x(t_j))
したがって、LFM2 Convと同様にLTCsをパラメトリックにしたものと見なせますが、$ \tau $に対して「良い」性質を導入しています。
$ \tau $は、時定数であり、正定値の時システムは安定(単調な減衰)になります。逆に、負値の場合は振動的/非減衰的挙動となり、好ましくありません。
SLC2ではLFM2 Convのこの課題に対して、時定数の符号安定性を改善することで対処しています。
具体的には、$ \alpha_{j-i}(t_j) \cdot A_{j-i} $は、非線形で負側を強く抑制するというSiLU関数の特性により、負ゲインの絶対値を小さくしています。
もちろんこれでは正定値になるわけではありませんが、学習時の確率分布が変わり学習安定性は向上します。
ReLUやSoftplus等の正定値を保証する関数もありますが、局所リプシッツ連続性や誤差伝搬時の取り扱い等を踏まえて、SiLU関数を採用しています。
実際、Mamba2においてもSiLU関数が採用されています。
また、
\begin{align}
SLC2(x_j) & = B(t_j) \cdot \sigma \left( \sum_{i=j-k}^j A_i^\prime(t_j) \cdot x_i \right) \\
& = B(t_j) \cdot \left( \sum_{i=0}^j A^\prime_{j-i}(t_j) \cdot x_{j-i} \right) \cdot \frac{1}{1-exp\left(- \sum_{i=0}^j A^\prime_{j-i}(t_j) \cdot x_{j-i} \right)}
\end{align}
ここで、
\begin{align}
a_{j-i} = exp(- A^\prime_{j-i}(t_j) \cdot x_{j-i}) \\
\Gamma_j = \sum_{i=0}^j A^\prime_{j-i}(t_j) \cdot x_{j-i}
\end{align}
とすると、
\begin{align}
SLC2(x_j) & \approx B(t_j) \cdot \Gamma_j \cdot \frac{1}{1 - \Pi_{i=0}^j a_{j-i}} \\
& = B(t_j) \cdot \Gamma_j \cdot \sum_{k=0}^\infty \Pi_{i=0}^j a_{j-i}^k
\end{align}
となり、局所領域おいてSequencial Semi-Separableに近い挙動となることが導かれます。
以上より、性質の「良い」演算であることが示せました。
なお、$ a_{j-i} $が十分小さい場合、
SLC2(x_j) \approx B^\prime(t_j) \cdot \Pi_{i=0}^j a_{j-i}
と近似することができます。ここからも、局所的なSequencial Semi-Separableを意識した演算であるというのはわかりやすいかと思われます。
7.2 SLC2のclass定義
LFM2 Convと同様にstep過程における逐次分解とclass内で完結したキャッシュ定義により高速実装を行うことができます。
下記にSimpleなSLC2 classを示します。
# Inference Cache class for SLC2
class SLCInferenceCache:
__slots__ = ("conv_state", "index", "kernel_size")
def __init__(self, conv_state: torch.Tensor, index: int = 0):
# conv_state: (batch, hidden_size, kernel_size)
self.conv_state = conv_state
self.index = int(index)
self.kernel_size = conv_state.size(-1)
@staticmethod
def alloc(
batch_size: int,
hidden_size: int,
kernel_size: int = 5,
device: Any = None,
dtype: Any = None
):
return SLCInferenceCache(
conv_state=torch.zeros(
batch_size,
hidden_size,
kernel_size,
device=device,
dtype=dtype
), index=0
)
def clear_(self):
self.conv_state.zero_()
self.index = 0
# SLC2 implementation
# Copyright 2025 Rikka Botan. All rights reserved
# coding = utf-8
# Licensed under "MIT License"
# Commercial use is of course permitted
class SLC2(nn.Module):
def __init__(
self,
config
):
"""
## Substitution Liquid Convolution Module
inspired by LFM2.LFM2ConvBlock
```
Formulation:
x ∈ ℝ^{B×S×E}
y ∈ ℝ^{B×S×E}
y = B ⋅ ∏ᵢ₌ⱼ⁽ʲ⁺ᵏ⁾ Aᵢ ⋅ xᵢ
----------------------------------------
Algorithm: SLC2
----------------------------------------
Input: x: (B, S, E)
Output: y: (B, S, E)
1: a, A, B, x₁ <- Linear(x)
2: x₂: (B, S, E) <- Convolution1D(E, E)(SiLU(a)*A*x₁)
3: x₃: (B, S, E) <- B*SiLU(x₂)
4: y: (B, S, E) <- Linear(x₃)
5: return y
----------------------------------------
```
"""
super().__init__()
self.n_embed = config.n_embd
self.n_head = config.n_head
self.d_head = config.n_embd//config.n_head
self.n_kernel = config.n_kernel
self.x_proj = nn.Linear(
in_features=self.n_embed,
out_features=self.n_embed,
bias=False
)
self.alpha_proj = nn.Linear(
in_features=self.n_embed,
out_features=self.n_head,
bias=False
)
self.A_proj = nn.Linear(
in_features=self.n_embed,
out_features=self.d_head,
bias=False
)
self.B_proj = nn.Linear(
in_features=self.n_embed,
out_features=self.n_embed,
bias=False
)
self.conv1d = nn.Conv1d(
in_channels=self.n_embed,
out_channels=self.n_embed,
kernel_size=self.n_kernel,
stride=1,
padding=self.n_kernel-1,
dilation=1,
groups=self.n_embed,
bias=False,
padding_mode="zeros"
)
self.c_proj = nn.Linear(
in_features=self.n_embed,
out_features=self.n_embed,
bias=False
)
self.cache: Optional[SLCInferenceCache] = None
def alloc_cache(
self,
batch_size: int,
device: Optional[torch.device] = None,
dtype: Optional[torch.dtype] = None
):
self.cache = SLCInferenceCache.alloc(
batch_size,
self.n_embed,
self.n_kernel,
device=device,
dtype=dtype
)
self.cache.conv_state = self.cache.conv_state.contiguous()
def clear_cache(
self
):
if self.cache is not None:
self.cache.clear_()
def forward(
self,
hidden_states: torch.Tensor,
use_cache: bool = False
) -> torch.Tensor:
bsz, seql, _ = hidden_states.size()
if seql > 1 or not use_cache:
x = self.x_proj(hidden_states)
alpha = self.alpha_proj(hidden_states)
A = self.A_proj(hidden_states)
B = self.B_proj(hidden_states)
A = A.unsqueeze(-2) * F.silu(alpha).unsqueeze(-1)
xA = self.conv1d(
(F.silu(A.reshape(bsz, seql, -1)) * x ).transpose(1, 2)).transpose(1, 2)
xA = F.silu(xA[:, :seql])
xAB = B * xA
y = self.c_proj(xAB)
return y
if self.cache is None or self.cache.conv_state.size(0) != bsz:
self.alloc_cache(
bsz,
device=hidden_states.device,
dtype=hidden_states.dtype
)
hidden_states, prefix = hidden_states[:, -1], hidden_states[:, :-1]
y_t = self.step(hidden_states, self.cache)
y = torch.cat([prefix, y_t.unsqueeze(1)], dim=1)
return y
def step(
self,
hidden_states: torch.Tensor,
cache: SLCInferenceCache
) -> torch.Tensor:
bsz = hidden_states.size(0)
x = self.x_proj(hidden_states)
alpha = self.alpha_proj(hidden_states)
A = self.A_proj(hidden_states)
B = self.B_proj(hidden_states)
A = A.unsqueeze(-2) * F.silu(alpha).unsqueeze(-1)
xA = F.silu(A.reshape(bsz, 1, -1)) * x
cache.conv_state.copy_(
torch.roll(cache.conv_state, shifts=-1, dims=-1))
cache.conv_state[:, :, -1] = xA.squeeze(1)
xA = torch.sum(
cache.conv_state
* rearrange(self.conv1d.weight, "d 1 w -> d w"),
dim=-1
) # (B D)
if self.conv1d.bias is not None:
xA = xA + self.conv1d.bias
xAB = B * F.silu(xA)
y_t = self.c_proj(xAB)
return y_t
7.3 SLC2を用いたリソース
SLC2を用いた言語モデルは下記から構築できます。
nanochatリポジトリのコードを編集して、どなたでも簡単に構築できるようにしています。
また、下記に示す通り、GQAの2/3をSLC2に入れ替えたnanochatはGQAのみからなるモデルと同等の性能を示しています。(推論速度は大きく向上しています。)
| Metric | GPT(karpathy/nanochat) | Saint Iberis |
|---|---|---|
| Total wall clock time | 3h51m | 3h15m |
| ARC-Challenge | 0.2807 | 0.2782 |
| ARC-Easy | 0.3876 | 0.3864 |
| HumanEval | 0.0854 | 0.0549 |
| MMLU | 0.3151 | 0.3166 |
| ChatCORE | 0.0844 | 0.2322 |
| Task Average | 0.1998 | 0.2190 |
英語バージョン:
日本語・英語バイリンガルバージョン:
使い方:
重み:
構成:
8.(付録②)Mamba2実装の解説 *56 *57 *58 *59
8.1 高速化・数値的安定化のための工夫点
(振り返り)Sequencial Semi-Separable(N-SSS)
\begin{align}
& \left\{
\begin{array}{ll}
h_t = A_th_{t-1} + B_tx_t \\
y_t = C_th_t
\end{array}
\right. \\
& h_t = \sum_{s=0}^t \bigl( \prod_{i=j+1}^t A_i \bigr)B_sx_s \\
& M_{ij} = C_j^TA_{i+1} \cdots A_j B_i \\
& M = diag(C) \cdot 1SS_{(a_{0:T})} \cdot diag(B) \\
& 1SS_{(a_{0:T})} = \begin{pmatrix}
1 & &&&\\
a_1 & 1 \\
a_2a_1 & a_2 & 1\\
\vdots & \vdots & \ddots & \ddots\\
a_{T-1}. . .a_1 & a_{T-1}...a_2 & \cdots & a_{T-1} & 1
\end{pmatrix}
\end{align}
Mamba2においては高速な演算のために下記の工夫を行っています。
![]() アインシュタイン縮約記法によるライブラリ内部最適化の積極的利用
アインシュタイン縮約記法によるライブラリ内部最適化の積極的利用
![]() 適切な初期化とパラメトライズによる演算簡易化
適切な初期化とパラメトライズによる演算簡易化
![]() segsumによる数値的安定化
segsumによる数値的安定化
![]() 対角成分と非対角成分を別計算することで効率化
対角成分と非対角成分を別計算することで効率化
特に最後の部分が重要かつ分かりにくい部分となっています。
M =
\left(
\begin{array}{c|c|c}
\begin{array}{ccc}
C_0^\top A_{0:0} B_0 \\
C_1^\top A_{1:0} B_0 & C_1^\top A_{1:1} B_1 \\
C_2^\top A_{2:0} B_0 & C_2^\top A_{2:1} B_1 & C_2^\top A_{2:2} B_2 \\
\end{array}
&& \\ \hline
\begin{array}{ccc}
\begin{bmatrix}
C_3^\top A_{3:2} \\
C_4^\top A_{4:2} \\
C_5^\top A_{5:2}
\end{bmatrix}
&
A_{2:2}
&
\begin{bmatrix}
B_0^\top A_{2:0} \\
B_1^\top A_{2:1} \\
B_2^\top A_{2:2}
\end{bmatrix}^\top \\
\end{array}
&
\begin{array}{ccc}
C_3^\top A_{3:3} B_3 \\
C_4^\top A_{4:3} B_3 & C_4^\top A_{4:4} B_4 \\
C_5^\top A_{5:3} B_3 & C_5^\top A_{5:4} B_4 & C_5^\top A_{5:5} B_5 \\
\end{array}
& \\ \hline
\begin{array}{ccc}
\begin{bmatrix}
C_6^\top A_{6:5} \\
C_7^\top A_{7:5} \\
C_8^\top A_{8:5}
\end{bmatrix}
&
A_{5:2}
&
\begin{bmatrix}
B_0^\top A_{2:0} \\
B_1^\top A_{2:1} \\
B_2^\top A_{2:2}
\end{bmatrix}^\top \\[12pt]
\end{array}
&
\begin{array}{ccc}
\begin{bmatrix}
C_6^\top A_{6:5} \\
C_7^\top A_{7:5} \\
C_8^\top A_{8:5}
\end{bmatrix}
&
A_{5:5}
&
\begin{bmatrix}
B_3^\top A_{5:3} \\
B_4^\top A_{5:4} \\
B_5^\top A_{5:5}
\end{bmatrix}^\top
\end{array}
&
\begin{array}{ccc}
C_6^\top A_{6:6} B_6 \\
C_7^\top A_{7:6} B_6 & C_7^\top A_{7:7} B_7 \\
C_8^\top A_{8:6} B_6 & C_8^\top A_{8:7} B_7 & C_8^\top A_{8:8} B_8
\end{array}
\end{array}
\right)
上記式のように時系列行列 M を、サイズ Q×Q のブロックに分割します。
このとき、非対角ブロックは、semiseparableの性質により低ランクに分解可能であり、複数のマトリックス積と再帰を組み合わせて効率的に処理できます。
また、非対角ブロックを対角ブロックに再帰させる操作は“小さな semiseparable 行列” とみなせます。
すなわち、これらはattention-likeな形式を使って並列に処理できます。
この分解により、ほとんどの演算が GPU で高速に並列化可能なマトリックス乗算に落とし込まれ、最終的な再帰はチャンクの数分に削減されます。
また、segsumは
a_{i:j}^\times = \exp\left( \sum_{t = i}^{j-1} \log a_t \right) = \exp\bigl( \mathrm{cumsum}(\log a)_j - \mathrm{cumsum}(\log a)_i \bigr)
のように表される演算です。
cumprodを対数空間上での和差で表現しています。
naiveな積商計算では、丸め誤差による数値精度悪化や underflow/overflowが問題となります。
この点を改善するためにsegsumが用いられています。
8.2 実装解説
Mamba2の実装は一見難しそうに見えますが、実は上記でお話しした内容を素直に実装しているだけです。
1.対角ブロックを計算
2.非対角ブロックで共有される状態を基に、非対角ブロックを並列で演算
3.1-SSを用いて再帰処理を行い、現在状態に対する寄与を算出
4.対角ブロックと非対角ブロックを組み合わせる。
という流れです。
# 和差による数値安定化を行うために対数空間上で計算
def segsum(x):
"""More stable segment sum calculation."""
T = x.size(-1)
x = repeat(x, "... d -> ... d e", e=T)
# maskを使って未来の要素の積を取らないようにする
mask = torch.tril(torch.ones(T, T, device=x.device, dtype=bool), diagonal=-1)
x = x.masked_fill(~mask, 0)
# 対数空間上で和を取る→積に相当
x_segsum = torch.cumsum(x, dim=-2)
mask = torch.tril(torch.ones(T, T, device=x.device, dtype=bool), diagonal=0)
# maskで-∞にすることでexpで戻したときに0になるようにする
x_segsum = x_segsum.masked_fill(~mask, -torch.inf)
return x_segsum
def ssd_minimal_discrete(X, A, B, C, block_len, initial_states=None):
"""
Arguments:
X: (batch, length, n_heads, d_head)
A: (batch, length, n_heads)
B: (batch, length, n_heads, d_state)
C: (batch, length, n_heads, d_state)
Return:
Y: (batch, length, n_heads, d_head)
"""
assert X.dtype == A.dtype == B.dtype == C.dtype
assert X.shape[1] % block_len == 0
# Rearrange into blocks/chunks
X, A, B, C = [rearrange(x, "b (c l) ... -> b c l ...", l=block_len) for x in (X, A, B, C)]
A = rearrange(A, "b c l h -> b h c l")
# チャンク内での積(チャンク間はsegsum)
A_cumsum = torch.cumsum(A, dim=-1)
# 1. Compute the output for each intra-chunk (diagonal blocks)
L = torch.exp(segsum(A))
# 対角ブロックの要素を計算
Y_diag = torch.einsum("bclhn,bcshn,bhcls,bcshp->bclhp", C, B, L, X)
# 2. Compute the state for each intra-chunk
# (right term of low-rank factorization of off-diagonal blocks; B terms)
# チャンク間で共有される潜在状態を低ランク(decay_state)で計算する
decay_states = torch.exp((A_cumsum[:, :, :, -1:] - A_cumsum))
states = torch.einsum("bclhn,bhcl,bclhp->bchpn", B, decay_states, X)
# 3. Compute the inter-chunk SSM recurrence; produces correct SSM states at chunk boundaries
# (middle term of factorization of off-diag blocks; A terms)
if initial_states is None:
initial_states = torch.zeros_like(states[:, :1])
# 1-SSを用いてチャンク間の再帰計算
states = torch.cat([initial_states, states], dim=1)
decay_chunk = torch.exp(segsum(F.pad(A_cumsum[:, :, :, -1], (1, 0))))
new_states = torch.einsum("bhzc,bchpn->bzhpn", decay_chunk, states)
states, final_state = new_states[:, :-1], new_states[:, -1]
# 4. Compute state -> output conversion per chunk
# (left term of low-rank factorization of off-diagonal blocks; C terms)
# 最終再帰状態から出力寄与を計算
state_decay_out = torch.exp(A_cumsum)
Y_off = torch.einsum('bclhn,bchpn,bhcl->bclhp', C, states, state_decay_out)
# Add output of intra-chunk and inter-chunk terms (diagonal and off-diagonal blocks)
# 対角ブロックと非対角ブロックの計算を統合
Y = rearrange(Y_diag+Y_off, "b c l h p -> b (c l) h p")
return Y, final_state
8.3 Mamba2の長距離文脈における議論 *24
Mamba2は学習時の系列長より長い系列が入力されたときに精度が悪化することが指摘されています。
\begin{array}{|ll|cccc|cccc|ccc|}
\hline
&& \text{S-NIAH-1} &&&&
\text{S-NIAH-2} &&&&
\text{S-NIAH-3} \\
&& \text{(pass-key retrieval)} &&&&
\text{(number in haystack)} &&&&
\text{(uuid in haystack)} \\ \hline
\text{Model} & &
1\text{K} & 2\text{K} & 4\text{K} & 8\text{K} &
1\text{K} & 2\text{K} & 4\text{K} & 8\text{K} &
1\text{K} & 2\text{K} & 4\text{K} \\ \hline
\text{DeltaNet} & &
97.4 & 96.8 & \mathbf{99.0} & \mathbf{98.8} &
98.4 & 45.6 & 18.6 & 14.4 &
85.2 & 47.0 & 22.4 \\ \hline
\text{Mamba2} & &
\mathbf{99.2} & \mathbf{98.8} & 65.4 & 30.4 &
99.4 & 98.8 & 56.2 & 17.0 &
64.4 & 47.6 & 4.6 \\ \hline
\mathbf{Gated\ DeltaNet} & &
98.4 & 88.4 & 91.4 & 91.8 &
\mathbf{100.0} & \mathbf{99.8} & \mathbf{92.2} & \mathbf{29.6} &
\mathbf{86.6} & \mathbf{84.2} & \mathbf{27.6} \\ \hline
\end{array}
この点について、内部状態のメモリ不足や記憶の一律減衰による忘却が原因であると指摘されています。私個人の見解としては、step過程においてcumprod処理を行うことによる数値的不安定性や、係数Aのスケールが学習時の系列長に依存してしまう点も重要であると考えています。論文 *24 でも提案されている通りgatingによる動的なメモリ選択性を強化することが重要かもしれません。
まとめ
LFM2 Convは速度・安定性の視点で優れた演算であることを解説してきました。
あくまで局所領域に限定された演算であるため、GQAなどのSelf Atentionベースのモジュールと一緒に使用することが前提となりますが、精度を維持したままモデルを高速化したい場合には有用なモジュールとなっています。
また、近年の状態空間モデルの流れや議論等もお話しさせていただきました。
もちろんまだ個々の手法にはそれぞれ課題があり、現在も研究が盛んに進められている分野になっています。
新しい手法が生まれ、「より良い性質」を与えていく過程が今後も楽しみだと考えています。
参考論文・サイト等
*1 'LFM2 を発表:市場最速のオンデバイス基盤モデル'
LiquidAIさんによるLFM2の発表記事です。
*2 'LiquidAI/LFM2-8B-A1B',
LFM2 MoE 8BA1BのModel cardです。
*3 'LiquidAI/LFM2-2.6B',
LFM2 2.6BのModel cardです。
*4 'LiquidAI/LFM2-1.2B',
LFM2 1.2BのModel cardです。
*5 'LiquidAI/LFM2-700M',
LFM2 700MのModel cardです。
*6 'LiquidAI/LFM2-350M',
LFM2 350MのModel cardです。
*7 'Introducing Liquid Nanos — frontier‑grade performance on everyday devices'
Liquid Nanosの紹介です。
*8 'LiquidAI/LFM2-1.2B-Extract'
情報抽出特化のLFM2-1.2Bファインチューニングモデルです。
*9 'LiquidAI/LFM2-350M-Extract'
情報抽出特化のLFM2-350Mファインチューニングモデルです。
*10 'LiquidAI/LFM2-350M-ENJP-MT'
短い文章の日英翻訳特化のLFM2-350Mファインチューニングモデルです。
*11 'LiquidAI/LFM2-1.2B-RAG'
RAG特化のLFM2-1.2Bファインチューニングモデルです。
*12 'LiquidAI/LFM2-1.2B-Tool'
tool calling特化のLFM2-1.2Bファインチューニングモデルです。
*13 'LiquidAI/LFM2-350M-Math'
数学特化のLFM2-350Mファインチューニングモデルです。
*14 'LiquidAI/LFM2-350M-PII-Extract-JP'
個人情報抽出・構造化特化のLFM2-350Mファインチューニングモデルです。
*15 'LiquidAI/LFM2-ColBERT-350M'
Re-ranker用のLFM2-350Mモデルです。
*16 'Liquid Time-constant Networks'
安定した有界動作と優れた表現力を実現している、液体時間定数ネットワーク(LTCs: Liquid Time-constant Networks)を提案している論文です。
*17 'Liquid Structural State-Space Models'
LTCsを用いてS4(Structural State Space Models)を改善した、 Liquid Structural State-Space Modelsを提案している論文です。
*18 'Attention Is All You Need'
Tranformerの原論文です。
*19 'Transformers are RNNs: Fast Autoregressive Transformers with Linear Attention'
Linear Attentionの原論文です。
*20 'Retentive Network: A Successor to Transformer for Large Language Models'
RetNetの原論文です。
*21 'Eagle and Finch: RWKV with Matrix-Valued States and Dynamic Recurrence'
Eagle(RWKV-5)とFinch(RWKV-6)の原論文です。
*22 'RWKV-7 "Goose" with Expressive Dynamic State Evolution'
Attention Free Transformer (AFT)による重み付きの和を状態更新に用いて、表現力を向上させたGoose(RWKV-7)を提案している論文です。記事中において線形モデリングの定式化部分等を引用しています。
*23 'Log-Linear Attention'
潜在状態を対数的なものとすることで効率化を志向する、Log-Linear-Attentionの原論文です。
*24 'Gated Delta Networks: Improving Mamba2 with Delta Rule'
ゲーティングを用いた状態更新により、特にロングコンテキストでの性能を向上させた、Gated Delta Networksを提案している論文です。
*25 'Kimi Linear: An Expressive, Efficient Attention Architecture'
Gated Delta Networkに対角要素を加えて改良したKimi Delta Attention (KDA)を提案している論文です。
*26 'HGRN2: Gated Linear RNNs with State Expansion'
外積による状態拡張メカニズムを用いて効率を向上させたモデル、HGRN2を提案している論文です。
*27 'Learning to (Learn at Test Time): RNNs with Expressive Hidden States'
隠れ状態をテストタイムにおいても学習可能にしたモデルである、Test-Time Training (TTT)を提案している論文です。
*28 'Longhorn: State Space Models are Amortized Online Learners'
オンライン凸計画法に基づきSSMsの状態更新を行う、Longhornを提案している論文です。
*29 'Efficiently Modeling Long Sequences with Structured State Spaces'
HIPPO行列を用いたStructured State Space sequence model (S4)を提案している論文です。
*30 'Simplified State Space Layers for Sequence Modeling'
S4のparallel scanによる効率化であるS5を提案している論文です。
*31 'Robustifying State-space Models for Long Sequences via Approximate Diagonalization'
S4におけるHIPPO行列の複雑性に対処するため、S4-PTD, S5-PTDを提案している論文です。
*32 'Mamba: Linear-Time Sequence Modeling with Selective State Spaces'
S4の係数をDynamicなものとし、Selection Mechanismを導入したMamba(S6)を提案している論文です。
*33 'Transformers are SSMs: Generalized Models and Efficient Algorithms Through Structured State Space Duality'
Matrixの分析からMamba(S6)とLinear Attentionには双対性があり、同一の枠組みで定式化できることを示しつつ、Mamba(S6)を高速化したMamba2を提案している論文です。
*34 'S7: Selective and Simplified State Space Layers for Sequence Modeling'
S5に対して選択的かつシンプルな状態更新を取り入れたS7を提案している論文です。
*35 'MEMMAMBA: RETHINKING MEMORY PATTERNS IN STATE SPACE MODEL'
Mamba2の長距離文脈での性能を改善するために、記憶減衰機構を再考し、 cross-layer and cross-tokenなattentionでメモリ補完を行う、MemMambaを提案している論文です。
*36 'Titans: Learning to Memorize at Test Time'
メモリ更新量をパラメトリックにすることで性能を向上させたニューラルメモリ、Titansを提案している論文です。
*37 'ATLAS: Learning to Optimally Memorize the Context at Test Time'
key, queryの多項式特徴写像の仕様とOmega RuleによりTitansより性能を向上させたニューラルメモリ、ATLASを提案している論文です。
*38 'Ultra-Sparse Memory Network'
スパースな構造でありながらメモリアクセスを効率化した、UltraMemを提案している論文です。
*39 'LM2: Large Memory Models'
CrossAttentionを用いてメモリモジュールとの混合を行う、LM2を提案している論文です。
*40 'MoBA: Mixture of Block Attention for Long-Context LLMs'
Attention Matrixをブロックに分割し、Top-kのブロックに対してのみSoftmax Attentionを行うことで効率を向上させた、MoBAを提案している論文です。
*41 'DeepSeek-V3.2-Exp: Boosting Long-Context Efficiency with DeepSeek Sparse Attention'
lightning indexerというAttention MatrixのTop-kスコアを求めるモジュールを用いつつ、MLAで高速化した、DSA: DeepSeek Sparse Attentionを提案している論文です。
*42 “Memory-efficient Transformers via Top-k Attention”
各クエリが参照すべきキー/値を全体ではなく「上位 k」だけに絞ることでメモリ・計算量を大幅に削減しつつ、性能低下が小さいことを示した論文です。
*43 “Top-Theta Attention: Sparsifying Transformers by Compensated Thresholding”
各クエリ/キー間の注意スコアにおいて、閾値 θ を超えるものだけを残す、Top-Theta Attentionを提案している論文です。
*44 'FlashAttention: Fast and Memory-Efficient Exact Attention with IO-Awareness',
GPU高帯域幅メモリ(HBM)とSRAM間のメモリの読み取り/書き込み数を減らすことで高速化する、FlashAttentionを提案している論文です。
*45 'FlashAttention-2: Faster Attention with Better Parallelism and Work Partitioning'
並列化・分散化によりFlash Attentionをさらに高速化した、FlashAttention2を提案している論文です。
*46 'FlashAttention-3: Fast and Accurate Attention with Asynchrony and Low-precision'
データ移動・アルゴリズムを改善し、Hopper GPUにおいてFlashAttention2をさらに高速化した、FlashAttention3を提案している論文です。
*47 'GQA: Training Generalized Multi-Query Transformer Models from Multi-Head Checkpoints'
*48 'ggml-org/llama.cpp'
C++で高速にLLMを動作させることのできるリポジトリです。
*49 'STAR: Synthesis of Tailored Architectures'
LIVsを構成単位としたニューラルアーキテクチャを自動的に設計・進化させるフレームワークを提案している論文です。
*50 'unslothai/unsloth'
unslothの公式リポジトリです。
*51 'axolotl-ai-cloud/axolotl'
axolotlの公式リポジトリです。
*52 'UnslothでLlama3をファインチューニングする'
unslothでのファインチューニング方法を解説した記事です。
*53 'Unsloth + TRL でLLMファインチューニングを2倍速くする'
unslothの解説記事です。
*54 'axolotlを使ったLLMのファインチューニング'
axolotlでのファインチューニング方法を解説した記事です。
*55 'LLMのファインチューニングのためのツール Axolotl'
axolotlの解説記事です。
*56 'state-spaces/mamba'
Mamba/Mamba2の公式実装です。
*57 'State Space Duality (Mamba-2) Part III - The Algorithm'
Mamba2のアルゴリズムに関する公式解説です。
*58 'mamba-2-matmul-free-models-june-papers-of-the-month'
Mamba2論文の紹介記事です。
*59 'Mamba-2: The ‘Transform’ation of Mamba'
Mamba2の解説記事です。
*60 'LTCsにおける順伝搬【解説】'
LTCsに関する簡易的な解説記事です。
*61 'Neural Ordinary Differential Equations'
ニューラルネットワーク + 常微分方程式 (ODE)のアプローチを確立した論文です。
*62 'Latent ODEs for Irregularly-Sampled Time Series'
不規則サンプリング時系列データにおいてODEベースモデルがRNNより高い性能を示した論文です。
*63 'MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications'
depthwise + pointwise convを用いて高効率な画像処理モデルを構築した研究です。
*64 'MobileNetV2: Inverted Residuals and Linear Bottlenecks'
MobleNetの後継研究です。
*65 'Depthwise Separable Convolutions for Neural Machine Translation'
Depthwise Separable Convolutionを翻訳タスクに用いた研究です。
執筆者:六花 牡丹(りっか ぼたん)
おさげとハーフツイン・可愛いお洋服が好きで、基本的にふわふわしている変わり者。
結構ドジで何もないところで転ぶタイプ。
人工知能に関しては独学のみ。