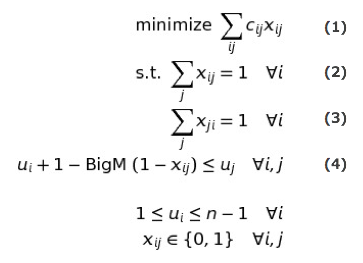巡回セールスマン問題から始まる数理最適化

この記事は BrainPad AdventCalendar 2017 8日目の記事です。
今回は数理最適化を取り上げてみようと思います。

ビジネス課題と数理最適化

BrainPadでは、データ分析に基づいて様々なビジネス課題に取り組んでいますが、業務貢献に寄与する最終段階で頻繁に検討されるのが数理最適化です。そこでは、様々な要素（例えば商品）に関する予測などを行った結果に基づき、どのような要素（商品）の組合せや割合が利益を最大化するのかを求めたりします。

今回はそのような問題の基礎例として、典型的な離散数理最適化問題である、”巡回セールスマン問題”を取り上げ、その定式化と解法の例を紹介できればと思います。

巡回セールスマン問題

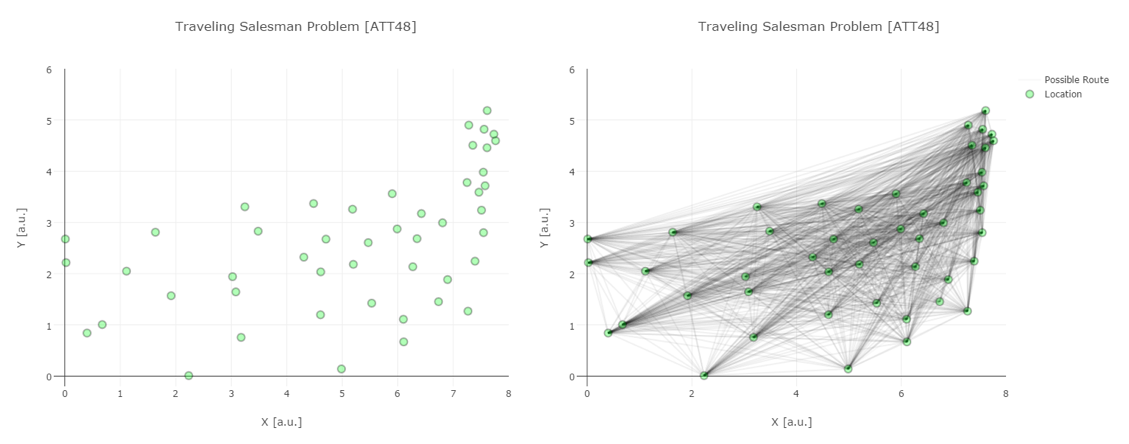
巡回セールスマン問題とは、下左図のような各拠点を必ず一回だけ通るという制約のもとで、距離が最小となる巡回ルートを見つける問題です。この例では$４８$拠点ですが、この例でも（初期拠点は固定しても一般性を失わないので）$47! \sim 10^{60}$ 通りのルートが存在し、しらみつぶしに探索していては、とても最小となる解は見つかりません。

そこで、数学的なアプローチを使ってより効率的に探索することで、リーズナブルな時間で解を見つけよう、とするわけです。実は世の中には最適化問題の解を見つける賢いライブラリ（ソルバー）が存在しており、様々な工夫が内部で施され、我々が詳細まで踏み込まなくても課題を解決できるように工夫されています。（詳細が気になる方は、まずは、[これなら分かる最適化数学―基礎原理から計算手法まで]などを参照いただくのがよいのかと思います。）

ソルバーには有償、無償、様々なものがありますが、今回は無償ソルバーCBCのpythonラッパーであるPuLPを用いて最適化問題を定式化、実行してみます。では、実際に定式化と実装を行ってみましょう。

問題の定式化

まずは、問題を数式に書き下してみると、解決すべき問題の見通しが良くなります。さらに、よく用いられる最適化のソルバーは、この数式を直感的に実装出来るように工夫されています。

先程の巡回セールスマン問題を定式化してみると、以下のようになります。

ここで $x_{ij}$ は、拠点iから拠点jに移動する場合に $1$ 、移動しない場合 $0$ となる二値の変数で、$c_{ij}$ がその間の移動距離を表す定数で、一般的に $i,j$ に対して非対象です。式 $(１)$ は 総距離の最小化 を表し、式 $(２)$ と $(３)$ が各拠点を 必ず一回だけ通る という条件を表していることはすぐに分かると思います。

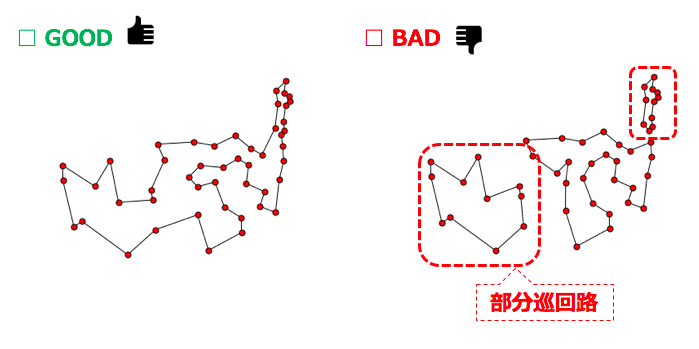
これでなんとなく、当初の目的が定式化されたように感じますが、実はこのままでは我々が求めたい巡回路の解は得られません。このままでは、下図の様な”部分巡回路”が解に含まれており、この様な解を除去しないと本当に欲しい 巡回ルート のみに探索が絞られていないのです。

部分巡回路の除去のためには様々なアプローチがあるのですが、その内の一つが式$(4)$で表される、”MTZ（ポテンシャル）制約”、と呼ばれている条件式です。そこでは、各拠点に補助変数 $u_{i}$ を導入して、訪問した順番に昇順で番号が振られるようになっています。部分巡回路が発生した場合は、番号が巡回の何処かで必ず降順になってしまうので、そのような解はこの制約によって除外されます。（正確には、スタート拠点 $i=0$では、$u_0=0$ とし、このスタート拠点の一点だけは降順が許されるように条件付けます。）

実際には昇順の番号が初めから振られるわけではなく、変数である$x_{i,j}$や$u_{i}$を上記、条件のなかで探索していく内に、自動的に訪問順序による番号が各拠点に付与されていきます。式 $(4)$ を見ていただくと、"BigM"と記載されていますが、これは”任意の大きい数”という意味です。もし拠点 $i$ から $j$ に移動した場合は $x_{i,j}=1$ となりますので、この式は $u_{i} + 1 \le u_{j}$ となり、 $u_{j}$ には $u_{i}+1$ より大きな値が入らなくてはなりません。一方、移動しない場合は $x_{i,j}=0$ ですので、この式は有効的には $- \text{BigM}\le u_{j}$ となり、 $u_{j}$ は $u_{i}$ に依らず任意の値を取って良い（ $u_{i}$ より小さくても良い）、ということになります。即ち、BigMの導入は $x_{ij}$ よるif分岐を可能にしていることが分かります。

パズルみたいですね。

問題の実装

さて、ここまで来ると後は実装なのですが、PuLPの場合は大変簡単で、以下のような手続きで最適化モデルと変数を定義し、評価指標と条件式を随時モデルに登録していくだけです。

まずはPuLPのインストールですが、予想通り

pip install pulp

一発。

定式化の実装については、（好き好きありましょうが）以下の通り大変直感的に行えます。

import pulp as pp

# 最適化モデルの定義
mip_model = pp.LpProblem("tsp_mip", pp.LpMinimize)


# 変数の定義
for i in range(N):
    for j in range(N):
        if i != j:
            x[i, j] = pp.LpVariable("x(%s,%s)"%(i, j), cat="Binary")

for i in range(N):
    u[i] = pp.LpVariable("u(%s)"%(i), cat="Continuous", lowBound=1.0, upBound=(N - 1.0))

# 評価指標（式（１））の定義＆登録
objective = pp.lpSum(c_[i, j] * x[i, j] for i in range(N) for j in range(N) if i != j)
mip_model += objective


#　条件式(2)の登録
for i in range(N):
    mip_model += pp.lpSum(x[i, j] for j in range(N) if i != j) == 1

# 条件式(3)の登録
for i in range(N):
    mip_model += pp.lpSum(x[j, i] for j in range(N) if i != j) == 1

# 条件式(4) (MTZ制約)
for i in range(N)
    for j in range(N):
        if i != j:
            mip_model += u[i] + 1.0 - BigM * (1.0 - x[i, j]) <= u[j]


# 最適化の実行
status = mip_model.solve()

# 結果の把握
print("Status: {}".format(pp.LpStatus[status]))
print("Optimal Value [a.u.]: {}".format(objective.value()))

PuLP以外の他のライブラリも多かれ少なかれ同様の手続きで実装が可能です。簡単ですね。

実行結果

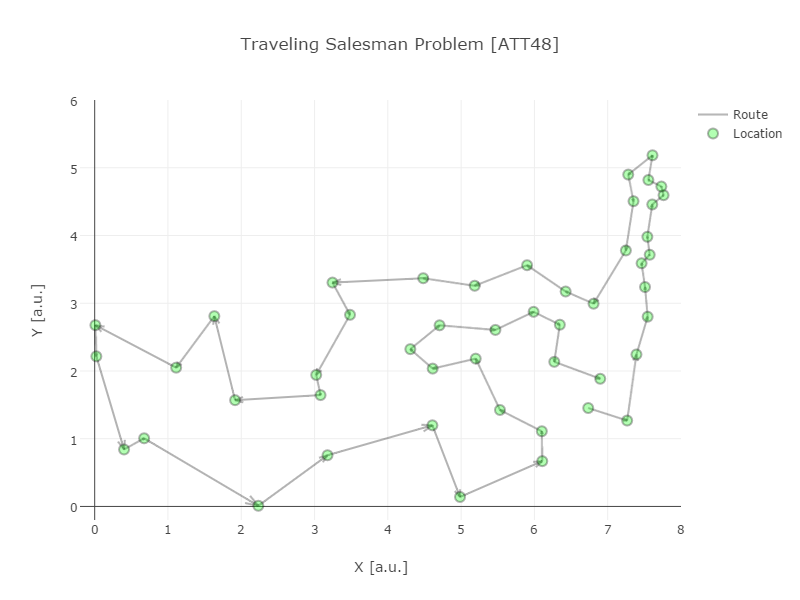
さて、一旦の実装が出来ましたので、実際に実行してみた結果をプロットしたのが、以下です。想定どおり、ちゃんと巡回路になっていますね。返り値のstatusもoptimalで、実際算出された距離、objective.value()、も尤もらしそうです。

今回の課題ではどうにか解くことができましたが、一方、実際の業務課題への適用を考えると、業務適用に耐えられるようなリーズナブルな時間で問題が解けるかは大変重要で、配慮が必要な点です。

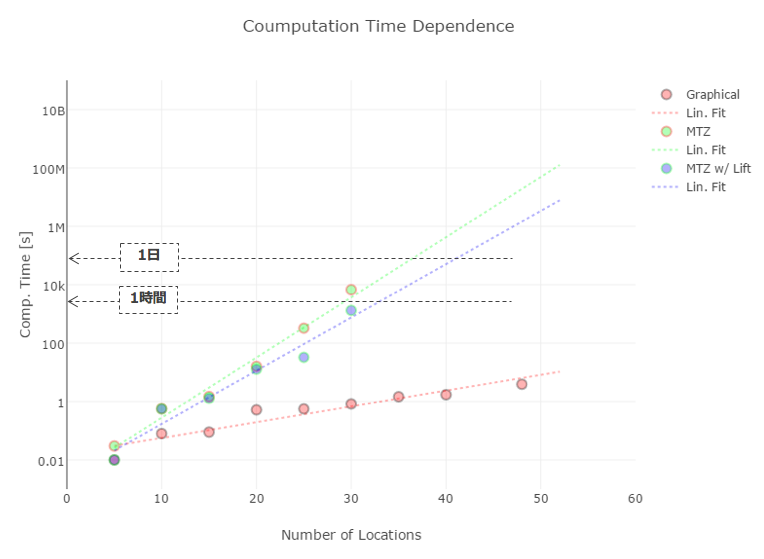
そこで、先程の実装を、拠点数を変化させながら実際に解いてみた際の実行時間をプロットしたのが以下の図の（緑）です。

縦軸が対数になっていることにご注意ください。ローカルの貧弱なPCで実行したものとはいえ、$30$拠点近くになると、残念ながら一般的な業務適用には耐えられない実行時間となることが分かります。

その為、最適化問題においては、尤もらしい初期解を与えるなど、より短い時間で解くための様々な工夫が模索されています。今回の問題でも、定式化に少々の工夫をすると、（赤）にまで計算時間を二桁！減らすことができます。今回用いたのは切除平面法という発見的方法を用いたものです（詳しくは章末に挙げた参考資料などをご参考ください）。

また、実際の業務適用に際しては、業務課題に応じた時間内で如何に解くか以外にも、人手による微調整の余地をどの程度残しどのように最適化問題に再度反映させるか、など配慮する必要があり、分析官の腕の見せ所となっています。

まとめ

今回は、ビジネス課題の解決においても頻繁に用いられる数理最適化の典型例として、巡回セールスマン問題を取り上げてみました。
その一見パズルのような定式化と容易な実装とともに、実際の業務適用においては、一層の工夫や配慮が必要であることが分かっていただければ幸いです。

もしさらなるご興味がありましたら、その他の離散最適化の例やアプローチ方法については
- [今日から使える!組合せ最適化]
- [あたらしい数理最適化: Python言語とGurobiで解く]
などを、連続最適化については
- [基礎系 数学 最適化と変分法]
- [機械学習のための連続最適化]
などを参照いただくとよいかと思います。

またBrainPadでは、最適化に関して以下のような試験的なアプローチも行っています。
- Adiabatic Quantum Computing Conference 2017
- 物理のいらない量子アニーリング入門

最適化の技術は、深層学習や強化学習の発展とともに今後もより一層発展していくものと思われますので、引き続き注意深く見守っていきたいと思っています。