RGB画像のみからの人の3D復元が今、熱い!?ということで論文を読んだので記事を書いてみます。
今まで3Dに触れたこともない素人なので間違っている箇所あれば編集リクエストなどお願いします。
SMPLモデル
画像からの人の3D復元タスクはSMPLモデルと呼ばれるものを使うのが多いようです。
SMPLモデルとはA Skinned Multi-Person Linear Modelという論文で提案されたパラメータによる操作が可能な人体モデルです。(図は論文Fig1より)
3Dモデルは一般的にとても複雑(mayaなどモデリングしている人すごい)なので、すべてのポリゴンを推定させようとすると困難です。そのため、あらかじめ低次元のパラメータで操作可能な人体モデルを作成することにより、3D推定をそのパラメータを推定させるタスクに置き換えることができます。
SMPLではheight,weight,(torso height)+(shoulder width),(chest breadth)+(neck height)などの10個の人のshapeを表す主成分特徴βと,72個のposeパラメータθを入力として1つの人体モデルが作ることができるようです。
βはSMPLモデルを作る際にデータセットの主成分分析を行い上位10個を用いているようです。
またposeパラメータの内訳は23個の関節のangleが関節1つにつき3つ、そして全体の向きを決定するglobal orientationが3つで3×23+3で72次元となります。
これにより,たとえばβのひとつ,左足の角度を連続的に変化させることにより簡単にポーズを変えることができます。

End-to-end Recovery of Human Shape and Pose
UCバークレーからのRGBからのSMPLモデルのパラメータ推定論文です。(Project page)

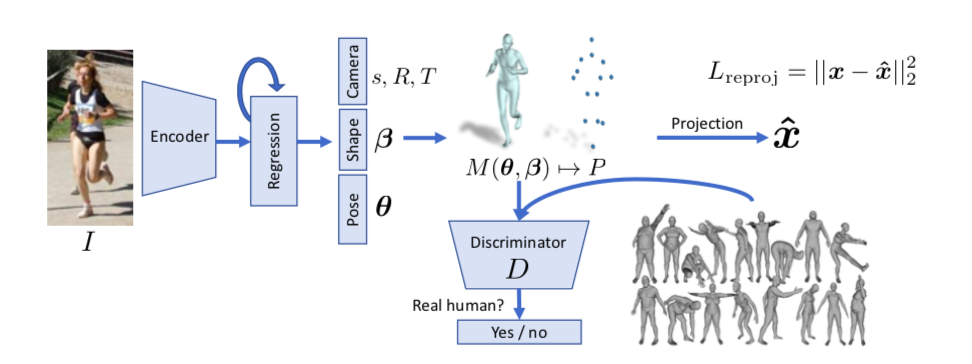
RGBからResnetベースでencodingしてSMPLモデルのβ、θを推定します。ただより正確な推定を行うために2次元平面へのreprojection LossとDiscriminator Lossを用いた学習をネットワークに追加しています。
reprojection Loss
3D復元の学習は学習データの作成がやはり難しくなります。またHuman3.6Mなどのデータセットは実験環境でデータが取られたこともあり、実際の煩雑な環境いわゆるin the wildな推定が困難とされてきました。そこでこの論文では2次元画像と3dモデルがunpairなデータセットでも学習できるようにSMPLモデルを2次元に投影し、2次元画像から取得した関節点座標とのlossをとるreporojection lossを提案しています。
θ、βを推定し、N=6980個の頂点をもつSMPLモデル
$M(\boldsymbol{\theta}, \boldsymbol{\beta}) \in \mathbb{R}^{3 \times \mathbb{N}}$
作成し,
keypoint頂点
$X(\boldsymbol{\theta}, \boldsymbol{\beta}) \in \mathbb{R}^{3 \times P}$
を得ます、
そしてさらにXをrotation,trasnlation,scaleのパラメータである
$R \in \mathbb{R}^{3 \times 3}$ ,$t \in \mathbb{R}^{2}$, $s \in \mathbb{R}$
を用いて2次元平面に投影します。
$\hat{\mathbf{x}}=s \Pi(R X(\boldsymbol{\theta}, \boldsymbol{\beta}))+t$
この$\hat{\mathbf{x}}$により、3Dモデルではなく2D正解データとのLossが計算できるようになります。よってencodeの段階ではθ、βだけではなくs,R,Tの推定も加えて85次元の$\Theta={\boldsymbol{\theta}, \boldsymbol{\beta}, R, t, s}$を推定します。
(θのglobal orientationがRのパラメータで取り込まれているのでθ=69次元になっている)
ただ、これを直接推定するのはかなり難しいらしく(特にR),iterative error feedbackと呼ばれる手法を用いています。iterative error feedbackは初期値$\Theta_{0}$を決め、従来の入力画像に$\Theta_{0}$を合わせたものを入力とします。ネットワークは$\Theta$ではなく目標値との残差$\Delta \Theta_{t}$を推定します。
そうして推定した$\Theta_{t+1}=\Theta_{t}+\Delta \Theta_{t}$を次の入力画像に加え推定を行うということにより、$\Delta \Theta_{t}$を最小化させ、段階的に推定精度を上げていくという手法のようです。参考論文 Human Pose Estimation with Iterative Error Feedback
また、3Dモデル正解データとの対応がとれる場合は勿論3Dモデル同士のLossが計算できて、頂点座標同士のLossと、β,θのパラメータLossを計算してreplojection lossに足すことができます。
adversarial Loss
いままで3Dモデルを2Dに投影したときのlossを話してきましたが、勿論2Dだけでは3Dの正確な推定には無理があるのでadversarial Lossというものを追加します。GANで用いられるDiscriminatorと同じように、入力が生成されたものか、それともリアルデータかを判別するネットワークを追加することにより、より自然な復元を目指します。安定的な学習を行うためDはshape,poseごとに別々のDを用います。さらにはpose自体にも関節点ごとに最終層だけ異なるlayerをもつDを準備します。全部でK+2個のDiscriminatorです。(K個の関節θでK個、βで1個,pose全てを合わせたkinematic treeで1個) その分ネットワークは浅くすみ、学習は安定するようです。 ちなみにGANで起こりがちなmode collapseはDを騙すだけでなく、reprojection lossの制約もあるのであまりなかったと書いてます。
これまでの話しをまとめると損失関数は次のようになります.3Dlossは省略化です
L=\lambda\left(L_{\text { reproj }}+\mathbb{1} L_{3 \mathrm{D}}\right)+L_{\mathrm{adv}}
L_{\text { reproj }}=\Sigma_{i}\left\|v_{i}\left(\mathbf{x}_{i}-\hat{\mathbf{x}}_{i}\right)\right\|_{1}
L_{3 \mathrm{D}}=L_{3 \mathrm{D} \text { joints }}+L_{3 \mathrm{D} \text { smpl }}
L_{\text { joints }}=\left\|\left(\mathbf{X}_{\mathbf{i}}-\hat{\mathbf{X}}_{\mathbf{i}}\right)\right\|_{2}^{2}
L_{\mathrm{smpl}}=\left\|\left[\boldsymbol{\beta}_{i}, \boldsymbol{\theta}_{i}\right]-\left[\hat{\boldsymbol{\beta}}_{i}, \hat{\boldsymbol{\theta}}_{i}\right]\right\|_{2}^{2}
\min L_{\mathrm{adv}}(E)=\sum_{i} \mathbb{E}_{\Theta \sim p_{E}}\left[\left(D_{i}(E(I))-1\right)^{2}\right]
\min L\left(D_{i}\right)=\mathbb{E}_{\Theta \sim p_{\mathrm{data}}}\left[\left(D_{i}(\Theta)-1\right)^{2}\right]+\mathbb{E}_{\Theta \sim p_{E}}\left[D_{i}(E(I))^{2}\right]
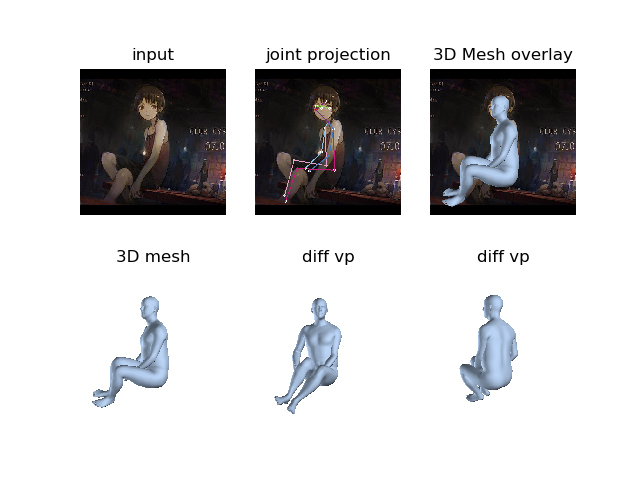
認識結果
2次絵画像でも認識しているのはすごいですね!今現在ならさらに高精度な推定が可能になっているはずなので楽しみです。
HMDやdensebodyなど主要論文をこれから追加していきたいです(いつになるかはわからない)