夜間光データと各国GDPの関係を調べる

はじめに

本記事では衛星データを用いて、世界各国のGDPと夜間光データの相関を調査します。
今回もGoogle Earth Engine(GEE)とGoogle Colabを用いて解析を行っていきます。
「まずそれなに？」という方は、以前初学者向けに書いた登りたい山を探す企画の記事があるので、ぜひご覧ください。
また、夜間光データについても、以前書いた夜間光データで2016年熊本地震の復興状況を調査してみた企画があるため、ぜひご覧ください。

各国のGDP情報を取得する

2015年と2016年のGDP情報を取得します。

まずは必要なライブラリをインポートします。

!pip -q -q -q install earthengine-api geopandas
!pip -q -q -q install datapackage

import geopandas as gpd
import datapackage
import pandas as pd
import ee
import numpy as np

次にDataHubからGDPデータを取得します。

2024/03/23現在、DataHubからJsonを取得できなくなっていました。
そのためDataHub.io/core/gdpからCSVをローカルにDLしてデータを読み込む形式に変更しました。
昔のコードは一応差分として表記しておきますので、実行時は+コード部分だけを実行してください。

# 年度の範囲を指定
start_year = 2015
end_year = 2016
year_list = [year for year in range(start_year, end_year+1)]

# GDPデータを取得
-data_url = 'https://datahub.io/core/gdp/datapackage.json'
-package = datapackage.Package(data_url)
-resources = package.resources
-for resource in resources:
-    if resource.tabular:
-        df_gdp = pd.read_csv(resource.descriptor['path'])
+filepath = 'ここにDLしたCSVファイルパスを入れてください（~/gdp.csv)'
+df_gdp = pd.read_csv(filepath)

# 指定した年度の範囲でデータを絞り込む
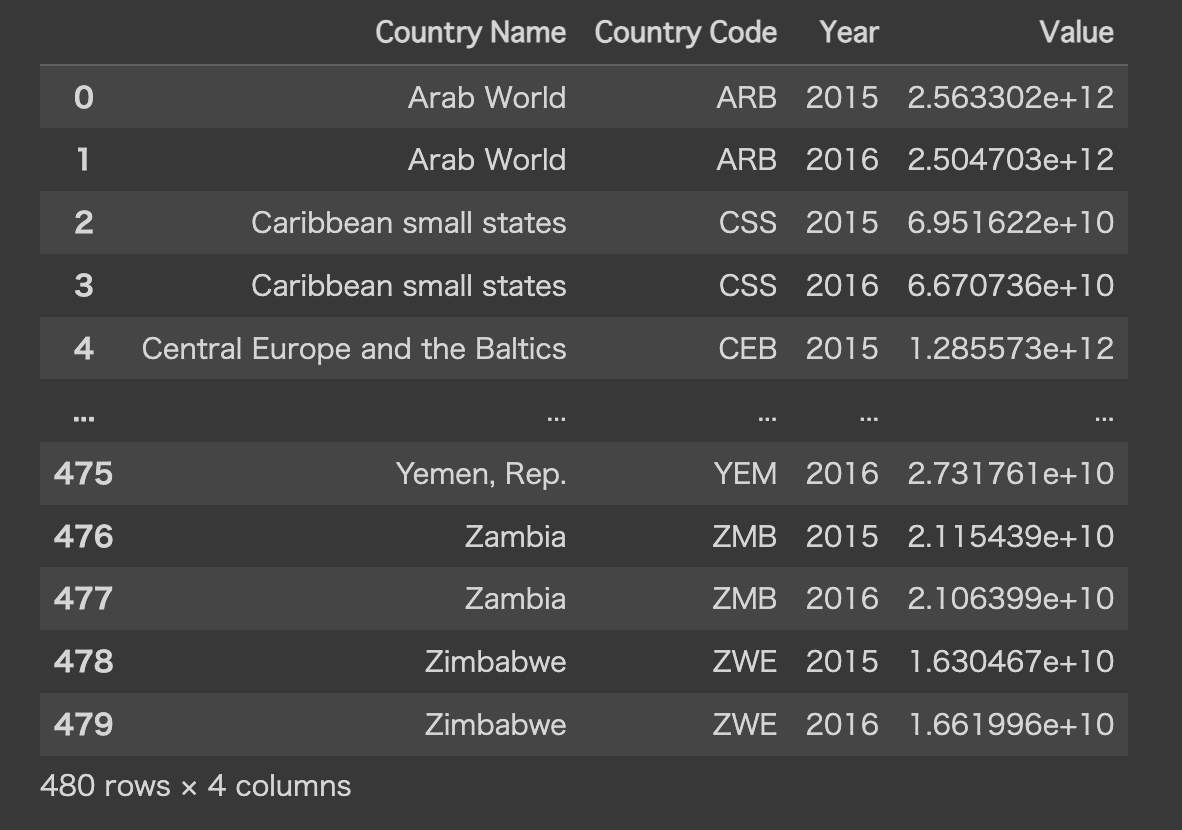
df_gdp = df_gdp[(df_gdp['Year'] >= start_year) & (df_gdp['Year'] <= end_year)].reset_index(drop=True)

df_gdp

以下のような結果が取得、df_gdpに格納されます。

各国の人口情報を取得する

次に各国の人口データを取得します。
今回は夜間光とGDPとの相関調査がメインですが、人口が多い国と少ない国で取得できる夜間光データに違いがあるかもしれないと思い取得しています。
直感的には、光の合計量が大きいほどGDPは高そうです。
それに加え、一人あたりの光の合計量との相関が強かったり、、、など何か特徴がないかついでに調べてみようと思った次第です。

import requests
import pandas as pd

# 各国の人口データを取得する
# df_gdpから国のISOコードを取得（GDPデータがある国のみ対象とする）
country_codes = df_gdp['Country Code'].unique()

# 空のDataFrameを作成
population_data = pd.DataFrame()

# 各国、各年に対してAPIを呼び出し
for country in country_codes:
    for year in range(start_year, end_year + 1):
        url = f'http://api.worldbank.org/v2/country/{country}/indicator/SP.POP.TOTL?date={year}&format=json'
        response = requests.get(url)
        data = response.json()

        # データが存在する場合、DataFrameに追加
        if data[1]:
            temp_df = pd.DataFrame(data[1])
            temp_df['country_code'] = country  # 'country_code'という列名にして一致させる
            temp_df['year'] = year
            population_data = pd.concat([population_data, temp_df])

# 不要な列を削除とデータの整形
population_data = population_data[['country_code', 'year', 'value']]
population_data.rename(columns={'value': 'population'}, inplace=True)

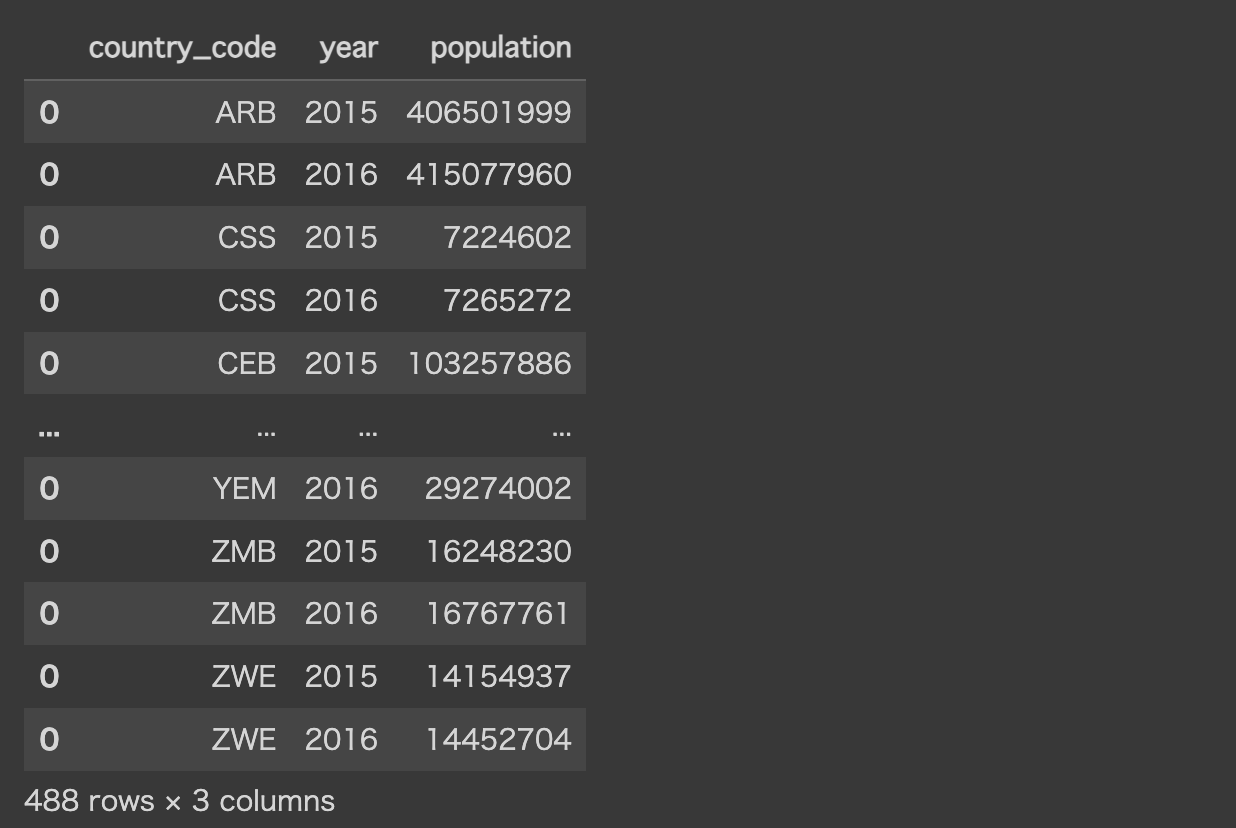
population_data

以下のような結果が取得、population_dataに格納されます。

各国のPolygon情報を取得する

次にcountry_codeごとのポリゴンデータを取得します。

2024/03/23現在、https://datahub.io/core/geo-countries/datapackage.json からJsonを取得できなくなっていました。
そのためNatural EarthからShapeファイルをローカルにDLしてデータを読み込む形式に変更しました。
※使用したデータは「Admin 0 – Countries」です。
昔のコードは一応差分として表記しておきますので、実行時は+コード部分だけを実行してください。

# 地理的なポリゴンデータを取得
-data_url = 'https://datahub.io/core/geo-countries/datapackage.json'
-package = datapackage.Package(data_url)
-resources = package.resources
-for resource in resources:
-    if resource.descriptor['format'] == "geojson":
-        df_poly = gpd.read_file(resource.descriptor['path'])
+shapefile_path = 'ここにDLしたSHPファイルパスを入れてください（~/ne_50m_admin_0_countries.shp)'
+df_poly = gpd.read_file(shapefile_path)
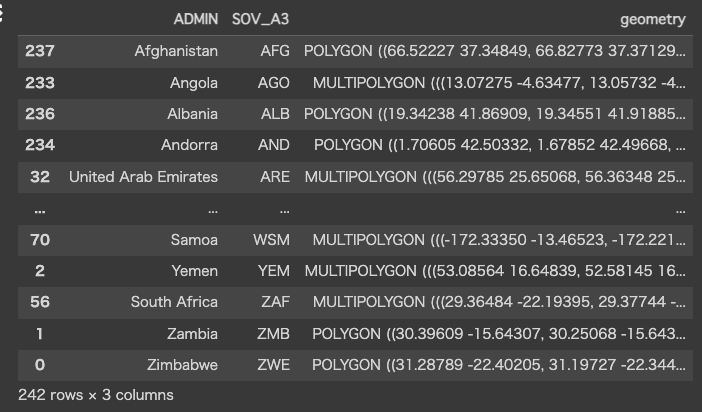
+df_poly = df_poly[['ADMIN', 'SOV_A3', 'geometry']].sort_values(by='SOV_A3')

df_poly

以下のような結果が取得、df_polyに格納されます。

各国の夜間光情報を取得する

夜間光はGEEのデータを使用するため、GEEの認証を行います。
GEE認証を実行すると認証に必要なURLが表示されるので、URLへアクセスしてGoogleアカウントを指定し、表示された認証コードをGoogle Colabのボックスへコピペしてください。

2024/03/23現在、ee.Initialize()はproject_idを指定せずに実行するとエラーになってしまうようです。
そのためee.Initialize(project='my-project')と記載するようにしてください。
つまり、このコードを実行する前にGoogleEearthEngineのプロジェクト登録が必要です。
昔のコードは一応差分として表記しておきますので、実行時は+コード部分だけを実行してください。

try:
       ee.Initialize()
except Exception as e:
       ee.Authenticate()
-       ee.Initialize()
+       ee.Initialize(project='ここにプロジェクトIDを入れてください')

今回使用するのはVIILSのデータです。

# VIIRSのデータを取得
viirs = ee.ImageCollection("NOAA/VIIRS/DNB/MONTHLY_V1/VCMSLCFG")
viirs = viirs.filter(ee.Filter.calendarRange(start_year, end_year, "year")).select("avg_rad")

また、いくつかの関数を定義します。

2024/03/23現在、国境ポリゴンをDatahub.ioからNatural Earthに変えたため、ISO_A3としていた箇所は全てSOV_A3に変更をしました。
ISO_A3とSOV_A3は異なる点もありますが基本一致しています。
両者の違いを簡単に記載しておきます。
ISO_A3は、国際標準化機構（ISO）によって定められた3文字の国コード（ISO 3166-1 alpha-3）を指します。これは各国を一意に識別するために広く使用されています。
一方で、SOV_A3は、主権国家を指す3文字のコードです。これは、いくつかの地域や国家が異なる政治的状況にある場合（例えば、一つの国が別の国を統治している場合など）に区別するために使われます。例えば、フランスの海外領土などが異なるSOV_A3コードを持つことがありますが、ISO_A3はフランス本国と同じです。

# shapelyのgeometryからGEEのgeometryに変換する関数
def get_aoi(code, df):
-    poly = df.loc[df['ISO_A3']==code, 'geometry'].values[0]
+    poly = df.loc[df['SOV_A3']==code, 'geometry'].values[0]
    if poly.geom_type =='MultiPolygon':
        g = [geom for geom in poly.geoms]
    else:
        g = [poly]
    features = []
    for i in range(len(g)):
        x,y = g[i].exterior.coords.xy
        coords = np.dstack((x,y)).tolist()
        features.append(coords)
    aoi = ee.Geometry.MultiPolygon(features)
    return aoi

# 合計光量を得る関数
def get_sumlight(img, aoi):
  sum = img.reduceRegion(reducer=ee.Reducer.sum(), geometry=aoi, scale=463.83, maxPixels=1e9).get('avg_rad').getInfo()
  return sum

# 平均光量を得る関数
def get_meanlight(img, aoi):
  mean = img.reduceRegion(reducer=ee.Reducer.mean(), geometry=aoi, scale=463.83, maxPixels=1e9).get('avg_rad').getInfo()
  return mean

# 最大値を得る関数
def get_maxlight(img, aoi):
  max = img.reduceRegion(reducer=ee.Reducer.max(), geometry=aoi, scale=463.83, maxPixels=1e9).get('avg_rad').getInfo()
  return max

# 面積を得る関数
def get_area(aoi):
    area = aoi.area().getInfo()
    return area

# 光量のばらつきを得る関数
def get_light_std(img, aoi):
    std = img.reduceRegion(reducer=ee.Reducer.stdDev(), geometry=aoi, scale=463.83, maxPixels=1e9).get('avg_rad').getInfo()
    return std

# 特徴量の計算
def get_features(collection, aoi):
    sum = get_sumlight(collection, aoi)
    mean = get_meanlight(collection, aoi)
    max = get_maxlight(collection, aoi)
    area = get_area(aoi)
    light_std = get_light_std(collection, aoi)

    return sum, mean, max, area, light_std

# 特徴量の計算実行
def compute_features(code, year):
    aoi = get_aoi(code, df_poly)
    viirs_filter = viirs.filter(ee.Filter.calendarRange(year, year, "year")).median()
    sum, mean, max, area, light_std = get_features(viirs_filter, aoi)
    gdp = df_gdp.loc[df_gdp['Country Code'] == code, 'Value'].values[0]
    return {'country': code, 'year': year, 'GDP': gdp, 'sumLight': sum, 'meanLight': mean, 'maxLight': max, 'area': area, 'lightStd': light_std}

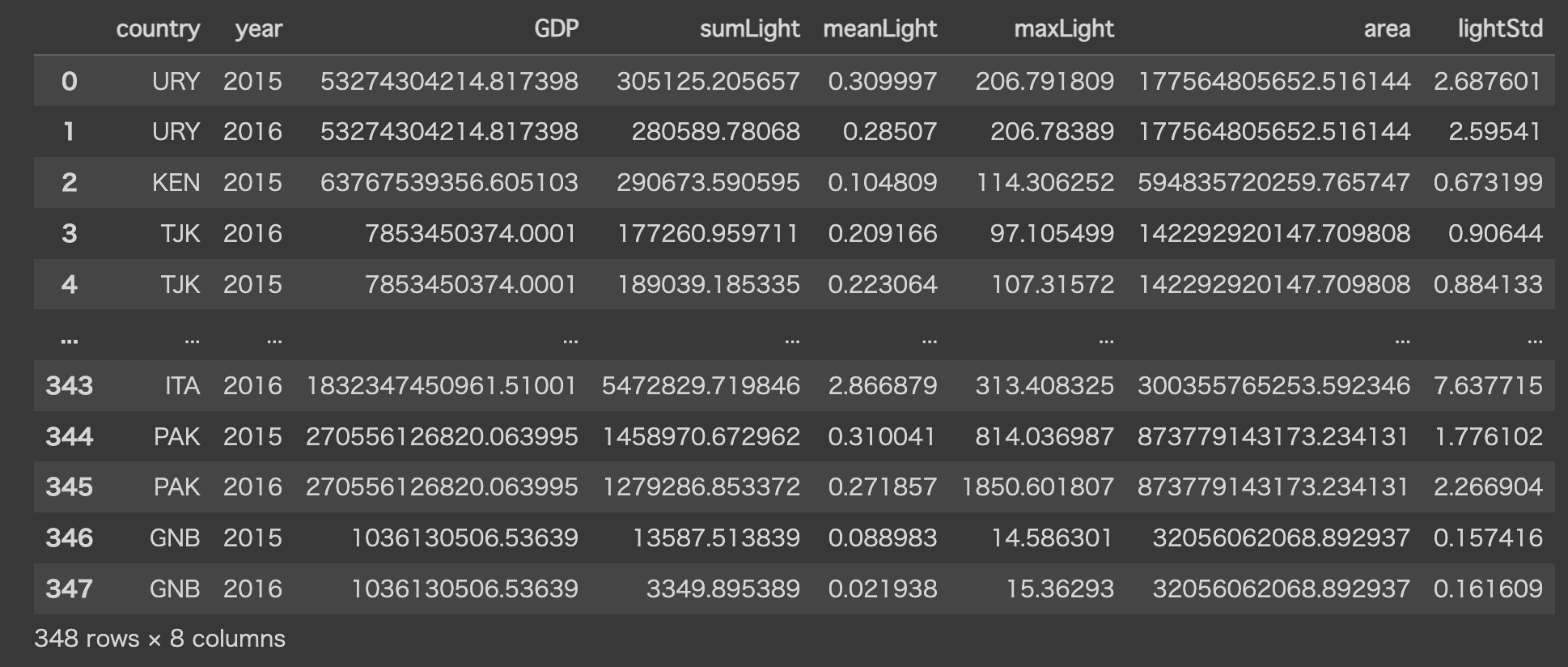
各国のGDPと上で定義した関数(合計光量、平均光量、最大光量、面積、光量のばらつき)を使って各値を計算し、変数に格納していきます。

# 結果を格納するDataFrameの準備
columns = ['country', 'year', 'GDP', 'sumLight', 'meanLight', 'maxLight', 'area', 'lightStd']
dataset = pd.DataFrame(columns=columns)

from concurrent.futures import ThreadPoolExecutor, as_completed

-# df_polyとdf_gdpの両方に存在する国のISO_A3コードのリストを作成
+# df_polyとdf_gdpの両方に存在する国のSOV_A3コードのリストを作成
-poly_countries = df_poly["ISO_A3"].values
+poly_countries = df_poly["SOV_A3"].values
gdp_countries = df_gdp['Country Code'].tolist()
common_countries = set(poly_countries).intersection(gdp_countries)
valid_countries = list(common_countries)

with ThreadPoolExecutor(max_workers=5) as executor:
    future_to_features = {executor.submit(compute_features, code, year): (code, year) for code in valid_countries for year in year_list}
    for future in as_completed(future_to_features):
        features = future.result()
        tmp_df = pd.DataFrame(features.values(), index=features.keys()).T
        dataset = pd.concat([dataset, tmp_df], axis=0, ignore_index=True)

dataset

以下のような結果が取得され、datasetに格納されます。

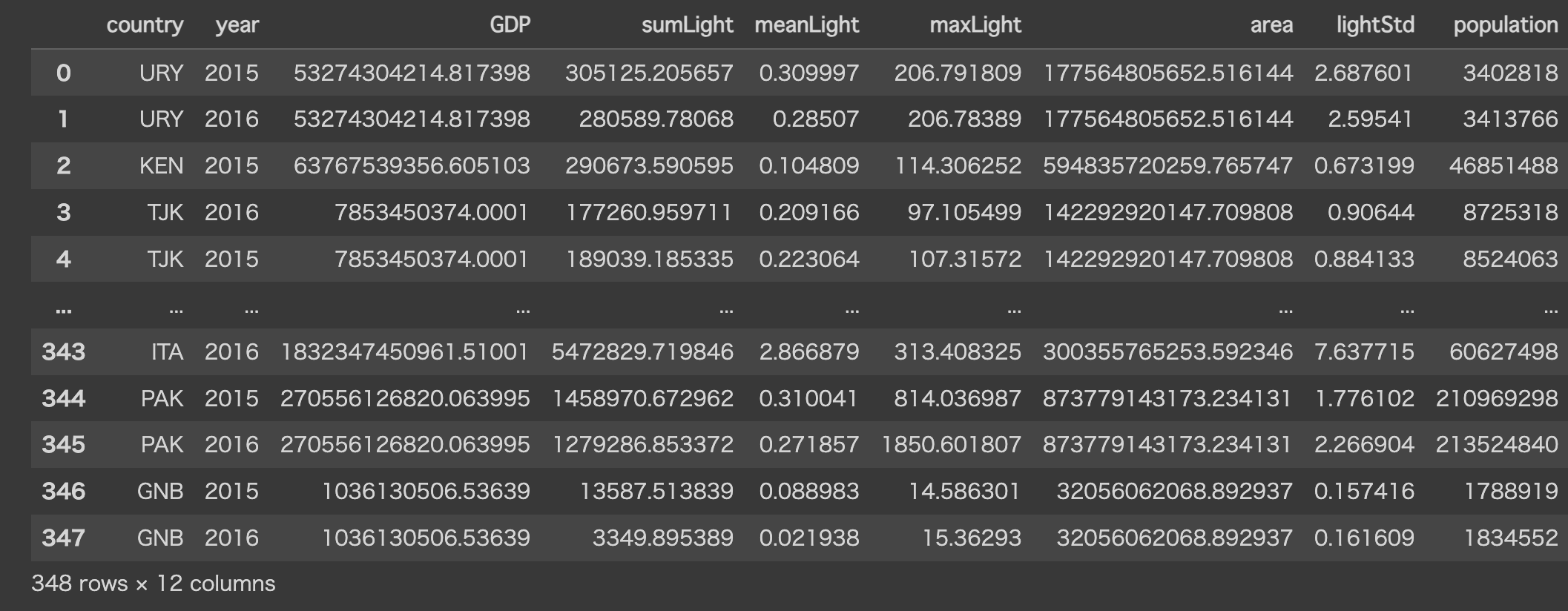
上述した通り、夜間光データに「一人あたりの」という概念を追加するため、人口データのデータセットを国コードと年のカラムをキーにマージします。

# datasetとpopulation_dataをマージし、結果をdatasetに直接格納
dataset = pd.merge(dataset, population_data, how='left', left_on=['country', 'year'], right_on=['country_code', 'year'])

# もし 'country_code' 列が不要な場合は削除
dataset.drop('country_code', axis=1, inplace=True)

# 人口一人あたりの特徴量作成
dataset['light_per_capita'] = dataset['sumLight'] / dataset['population']
dataset['meanLight_per_capita'] = dataset['meanLight'] / dataset['population']
dataset['maxLight_per_capita'] = dataset['maxLight'] / dataset['population']

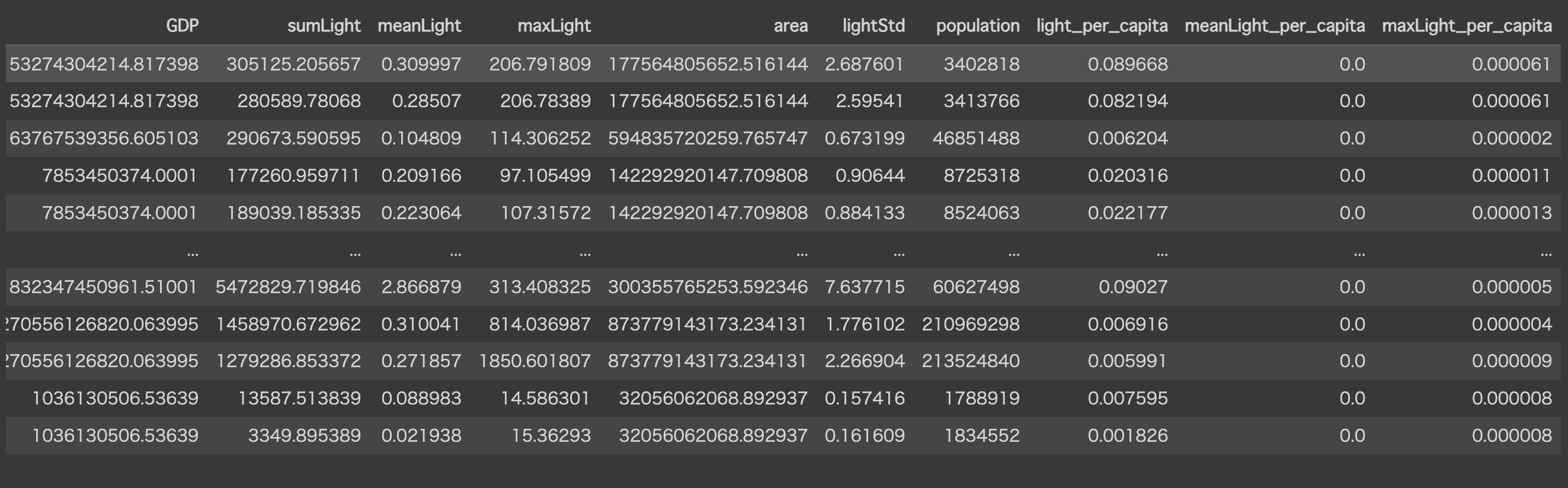
dataset

以下のような結果が取得、datasetに格納されます。

特徴量のグラフ化

モデルを作る前に各特徴量の概形を知るため一旦グラフ化してみます。

# 各特徴量の分布
import matplotlib.pyplot as plt
import numpy as np

fig, axes = plt.subplots(4, 2, figsize=(10, 20))

X = dataset.drop(columns=['country', 'year', 'GDP']).astype('float64')  # countryとyear,GDP以外のすべての列が特徴量

num_columns = X.shape[1]  # Xの列数を取得
i = 0

for ax in axes:
    for a in ax:
        if i < num_columns:  # iが列数より小さい場合のみ処理を行う
            _, bins = np.histogram(X.iloc[:, i], bins=50)
            a.hist(X.iloc[:, i].values, bins=bins, alpha=0.5)
            a.set_title(X.columns[i])
            i += 1
        else:
            a.axis('off')  # 残りのサブプロットを非表示にする

plt.tight_layout()

以下のような分布図になりました。
各特徴量の値は小さく、かつ集中していることくらいしか分かりませんね。

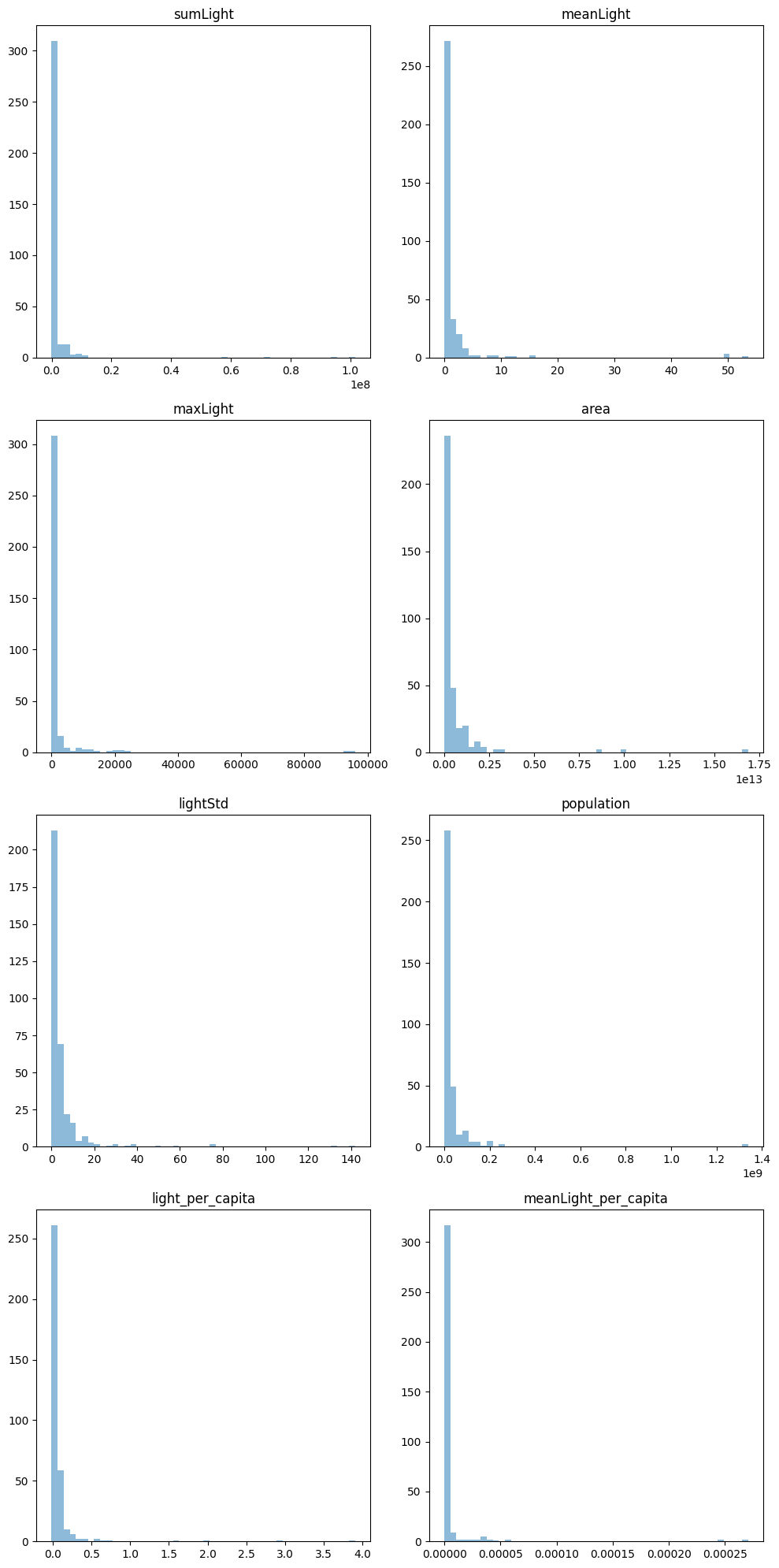
続いて各特徴量とGDPとの散布図を表示してみます。

# 各特徴量とGDPとの散布図表示

import seaborn as sns
import matplotlib.pyplot as plt

features = [col for col in dataset.columns if col not in ['country', 'year', 'GDP']]

fig, axes = plt.subplots(len(features) // 3 + len(features) % 3, 3, figsize=(15, 15))
fig.tight_layout(pad=5.0)

for ax, feature in zip(axes.ravel(), features):
    sns.scatterplot(data=dataset, x=feature, y='GDP', ax=ax)
    ax.set_title(f'{feature} vs GDP')
    ax.set_xlabel(feature)
    ax.set_ylabel('GDP')

# 余分なサブプロットを非表示にする
for remaining_ax in axes.ravel()[len(features):]:
    remaining_ax.axis('off')

plt.show()

以下のような散布図になりました。
線形って感じもしないですね。

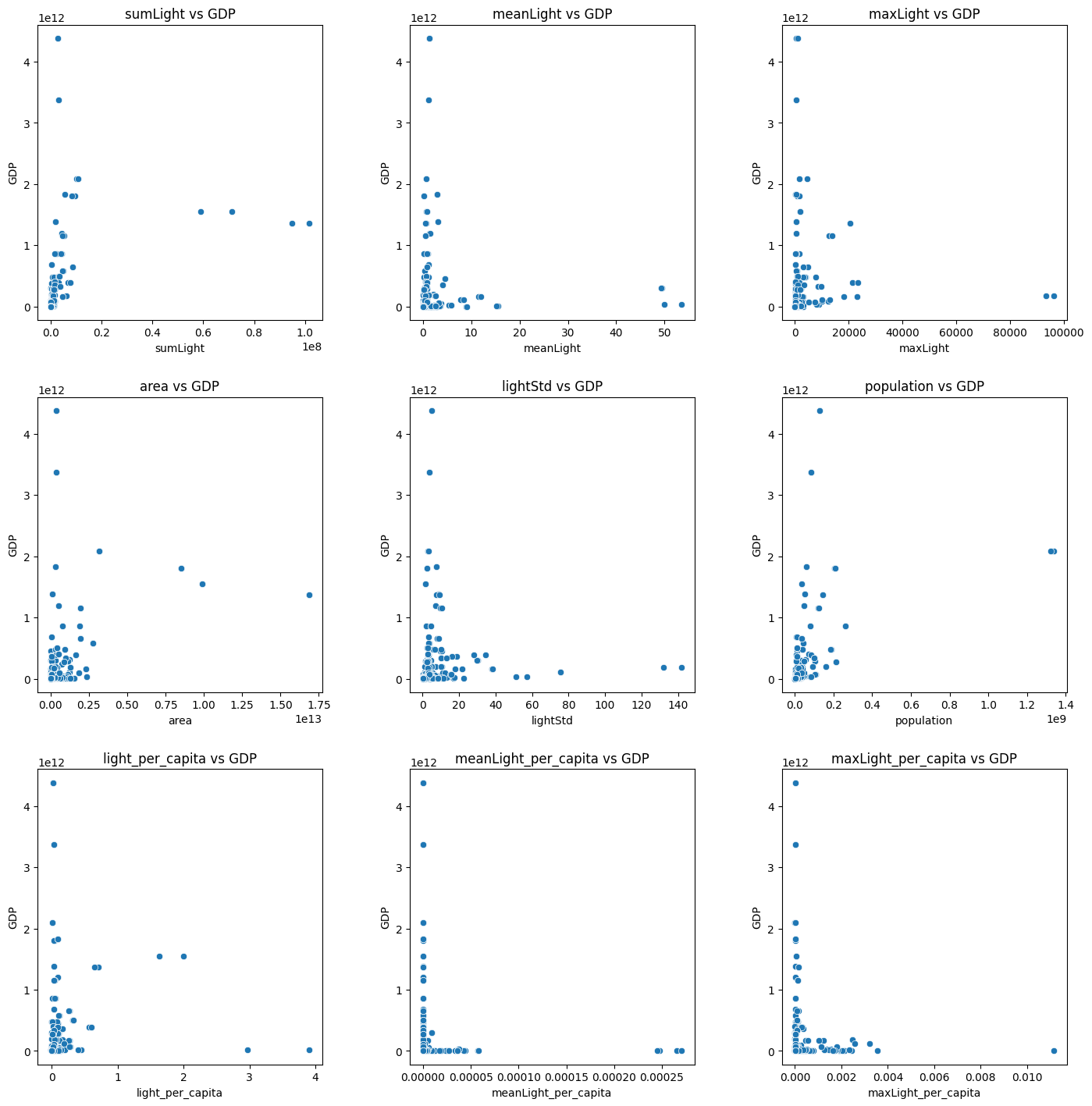
外れ値の除外

上記のグラフを見ていて外れ値がありそうなことがわかったので外れ値を除外していきます。
標準偏差からしきい値を決め、そこから外れている値は削除していきます。
今回はしきい値=1σ分にしています。

from scipy import stats
import numpy as np

# オブジェクト型の列を数値型に変換
dataset[features] = dataset[features].apply(pd.to_numeric, errors='coerce')

# NaN（変換できなかった値）を除去
dataset.dropna(subset=features, inplace=True)

# Z-Scoreを計算(Z=(X-μ)/σ X:個々のデータ点, μ:データセットの平均, σ:標準偏差)
z_scores = np.abs(stats.zscore(dataset[features]))

# 閾値を設定（σと同義）
threshold = 1

# 外れ値を含まない行だけを抽出
dataset = dataset[(z_scores < threshold).all(axis=1)]

ここでは表示しませんが、z_scoresに各行の各値の偏差がどれくらいかが計算されています。
今回はその値が1未満だった行だけ使うことにしました。
除去後の散布図は以下になります。
外れ値が除去され、多少なり分布が見やすくなりました。

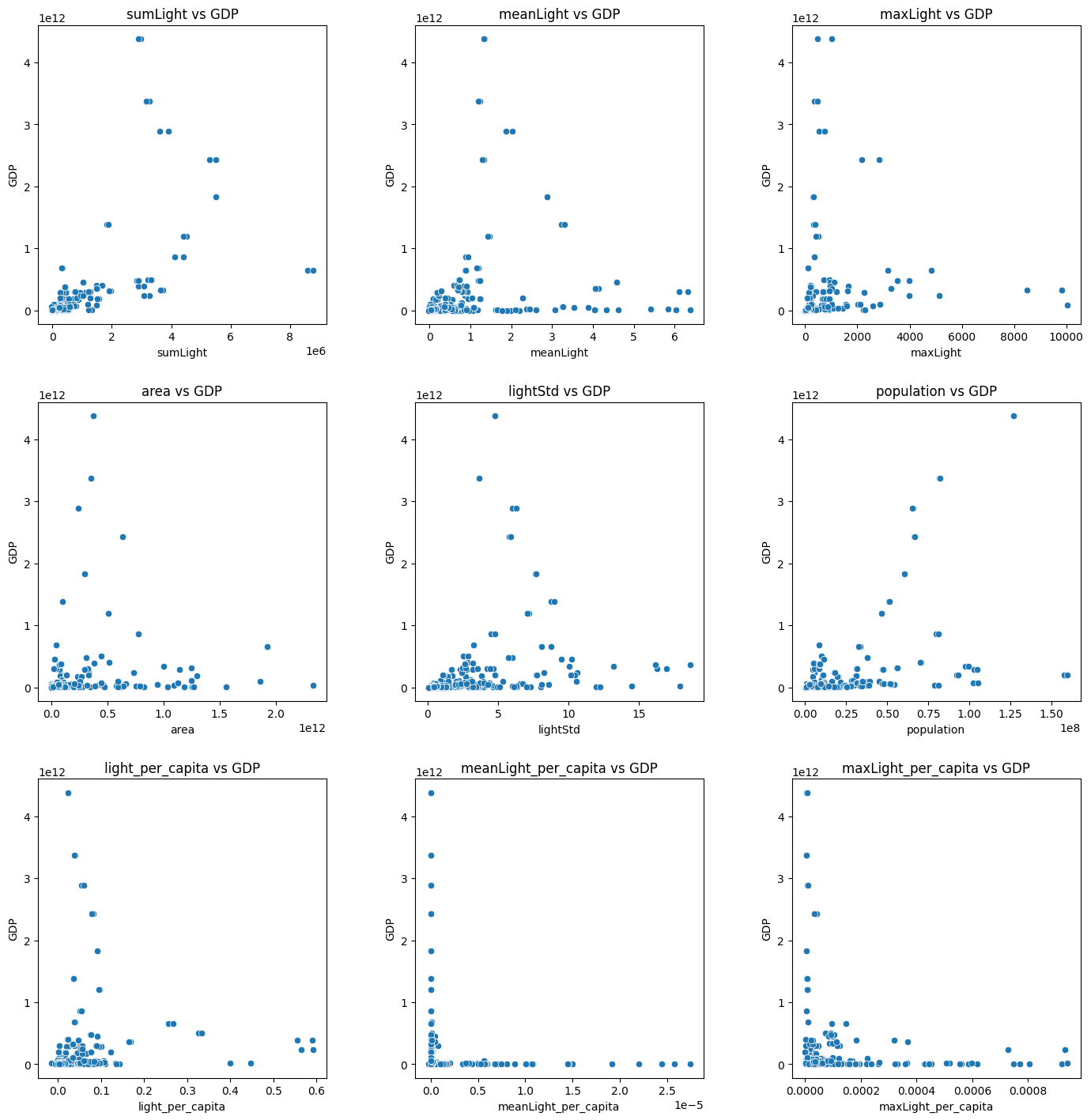
機械学習の実行

ここからは機械学習のモデル作成に入っていきます。
あまり線形にも見えないですし、どのモデルが効果的なのかが不明だったためいろいろ試してみました。
まずはトレーニング用のデータとテスト用のデータでデータセットを分けます。

from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score

# 特徴量とターゲットを分割
X = dataset.drop(columns=['country', 'year', 'GDP']).astype('float64')  # countryとyear,GDP以外のすべての列が特徴量
y = dataset['GDP'].astype('float64')

# データをトレーニングセットとテストセットに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

線形回帰モデル

from sklearn.linear_model import LinearRegression

# 線形回帰モデルの作成とトレーニング
lr_model = LinearRegression()
lr_model.fit(X_train, y_train)

# 線形回帰モデルの評価
y_pred_lr = lr_model.predict(X_test)
mse_lr = mean_squared_error(y_test, y_pred_lr)
r2_lr = r2_score(y_test, y_pred_lr)

# 評価結果を表示
print("LinearRegression Model:")
print(f"Mean Squared Error: {mse_lr}")
print(f"R^2 Score: {r2_lr}\n")

線形回帰モデルの結果は以下でした。

LinearRegression Model:
Mean Squared Error: 2.1204141057641096e+23
R^2 Score: 0.5570300034041327

SVMモデル

from sklearn.svm import SVR

# SVMモデルの作成とトレーニング
svm_model = SVR()
svm_model.fit(X_train, y_train)

# SVMモデルの評価
y_pred_svm = svm_model.predict(X_test)
mse_lr = mean_squared_error(y_test, y_pred_svm)
r2_svm = r2_score(y_test, y_pred_svm)

# 評価結果を表示
print("SVM Model:")
print(f"Mean Squared Error: {mse_lr}")
print(f"R^2 Score: {r2_svm}\n")

SVMモデルの結果は以下でした。

SVM Model:
Mean Squared Error: 5.2807506397751024e+23
R^2 Score: -0.1031873852215508

決定木モデル

from sklearn.tree import DecisionTreeRegressor

# 決定木モデルの作成とトレーニング
tree_model = DecisionTreeRegressor(random_state=42)
tree_model.fit(X_train, y_train)

# 決定木モデルの評価
y_pred_tree = tree_model.predict(X_test)
mse_tree = mean_squared_error(y_test, y_pred_tree)
r2_tree = r2_score(y_test, y_pred_tree)

# 評価結果を表示
print("Decision Tree Model:")
print(f"Mean Squared Error: {mse_tree}")
print(f"R^2 Score: {r2_tree}\n")

決定木モデルの結果は以下でした。

Decision Tree Model:
Mean Squared Error: 2.6236787804198564e+23
R^2 Score: 0.45189433645442567

ランダムフォレストモデル

from sklearn.ensemble import RandomForestRegressor

# ランダムフォレストモデルの作成とトレーニング
forest_model = RandomForestRegressor(random_state=42)
forest_model.fit(X_train, y_train)

# ランダムフォレストモデルの評価
y_pred_forest = forest_model.predict(X_test)
mse_forest = mean_squared_error(y_test, y_pred_forest)
r2_forest = r2_score(y_test, y_pred_forest)

# 評価結果を表示
print("Random Forest Model:")
print(f"Mean Squared Error: {mse_forest}")
print(f"R^2 Score: {r2_forest}")

ランダムフォレストモデルの結果は以下でした。

Random Forest Model:
Mean Squared Error: 1.556106609116825e+23
R^2 Score: 0.6749179617936525

LightGBM(Light Gradient Boosting Machine)モデル

import lightgbm as lgb

# データセットの作成
train_data = lgb.Dataset(X_train, label=y_train)
test_data = lgb.Dataset(X_test, label=y_test, reference=train_data)

# パラメータの設定
params = {
    'boosting_type': 'gbdt',
    'objective': 'regression',
    'metric': {'l2', 'l1'},
    'num_leaves': 31,
    'learning_rate': 0.05,
    'feature_fraction': 0.9,
    'bagging_fraction': 0.8,
    'bagging_freq': 5,
    'verbose': 0
}

# モデルのトレーニング
num_round = 100
lgbm_model = lgb.train(
    params,
    train_data,
    num_round,
    valid_sets=[test_data],
    callbacks=[lgb.early_stopping(stopping_rounds=10)]
)

# 予測
y_pred_lgbm = lgbm_model.predict(X_test, num_iteration=lgbm_model.best_iteration)

# 評価
mse_lgbm = mean_squared_error(y_test, y_pred_lgbm)
r2_lgbm = r2_score(y_test, y_pred_lgbm)

# 評価結果を表示
print("LightGBM Model:")
print(f"Mean Squared Error: {mse_lgbm}")
print(f"R^2 Score: {r2_lgbm}")

LightGBMモデルの結果は以下でした。

LightGBM Model:
Mean Squared Error: 2.5184645195733786e+23
R^2 Score: 0.4738743641491602

ニューラルネットワークモデル

from sklearn.neural_network import MLPRegressor
from sklearn.model_selection import GridSearchCV

# パラメータのグリッドを定義
param_grid = {
    'hidden_layer_sizes': [(100, 50), (50, 25), (100,)],
    'activation': ['tanh', 'relu'],
    'solver': ['sgd', 'adam'],
    'alpha': [0.0001, 0.001, 0.01],
    'learning_rate': ['constant', 'adaptive']
}

# MLPRegressor のインスタンスを作成
mlp = MLPRegressor(max_iter=1000)

# GridSearchCV のインスタンスを作成
grid_search = GridSearchCV(mlp, param_grid, cv=3, scoring='neg_mean_squared_error', n_jobs=-1)

# グリッドサーチを実行
grid_search.fit(X_train, y_train)

# 最適なハイパーパラメータを表示
print("Best Hyperparameters:", grid_search.best_params_)

# 最適なモデルで評価
best_mlp = grid_search.best_estimator_
y_pred = best_mlp.predict(X_test)

# 評価
rmse = np.sqrt(mean_squared_error(y_test, y_pred))
r2_score = r2_score(y_test, y_pred)
print(f"Test RMSE with Neural Network: {rmse}")
print(f"Test R2SCORE with Neural Network: {r2_score}")

ニューラルネットワークモデルの結果は以下でした。

Test RMSE with Neural Network: 696901687615.265
Test R2SCORE with Neural Network: -0.01460420800851181

結果だけ見るとランダムフォレストモデルが一番正答率が高かったです。
ただし、クロスバリデーションを行うとランダムフォレストモデルを採用しても使える結果にはなりませんでした。
以下にクロスバリデーションの実施と、各実行時のトレーニングとテストデータで使われたデータの分布を表示するコードを記載します。

# ランダムフォレストクロスバリデーション

from sklearn.model_selection import KFold
from sklearn.metrics import r2_score
from sklearn.ensemble import RandomForestRegressor

cv = KFold(n_splits=5)

r2_scores = []

for fold_num, (train_index, test_index) in enumerate(cv.split(X, y), 1):
    X_train, X_test = X.loc[train_index], X.loc[test_index]
    y_train, y_test = y.loc[train_index], y.loc[test_index]

    # モデルを訓練
    model = RandomForestRegressor()
    model.fit(X_train, y_train)

    y_pred = model.predict(X_test)

    # R2スコアを計算
    r2 = r2_score(y_test, y_pred)
    r2_scores.append(r2)

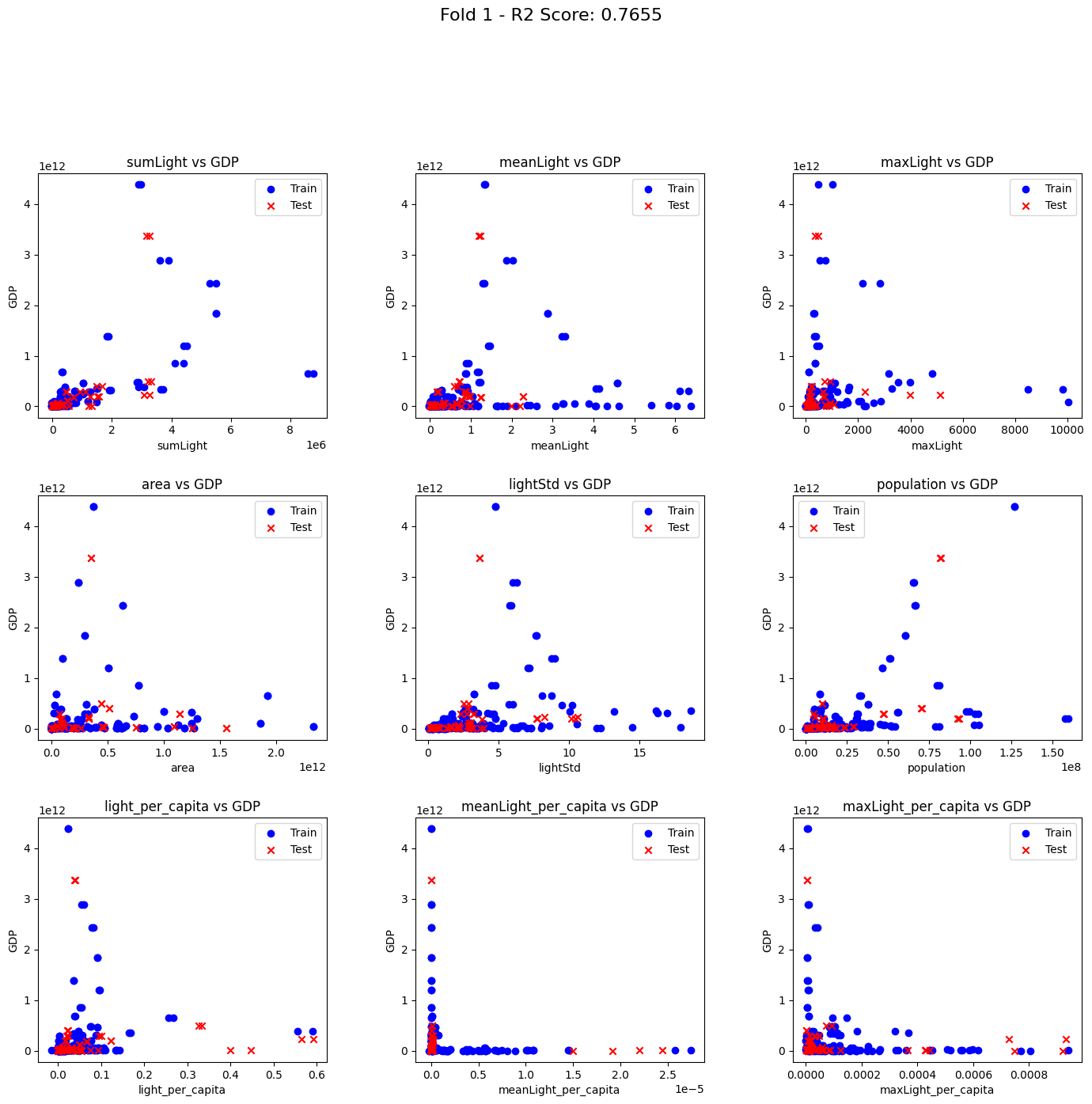
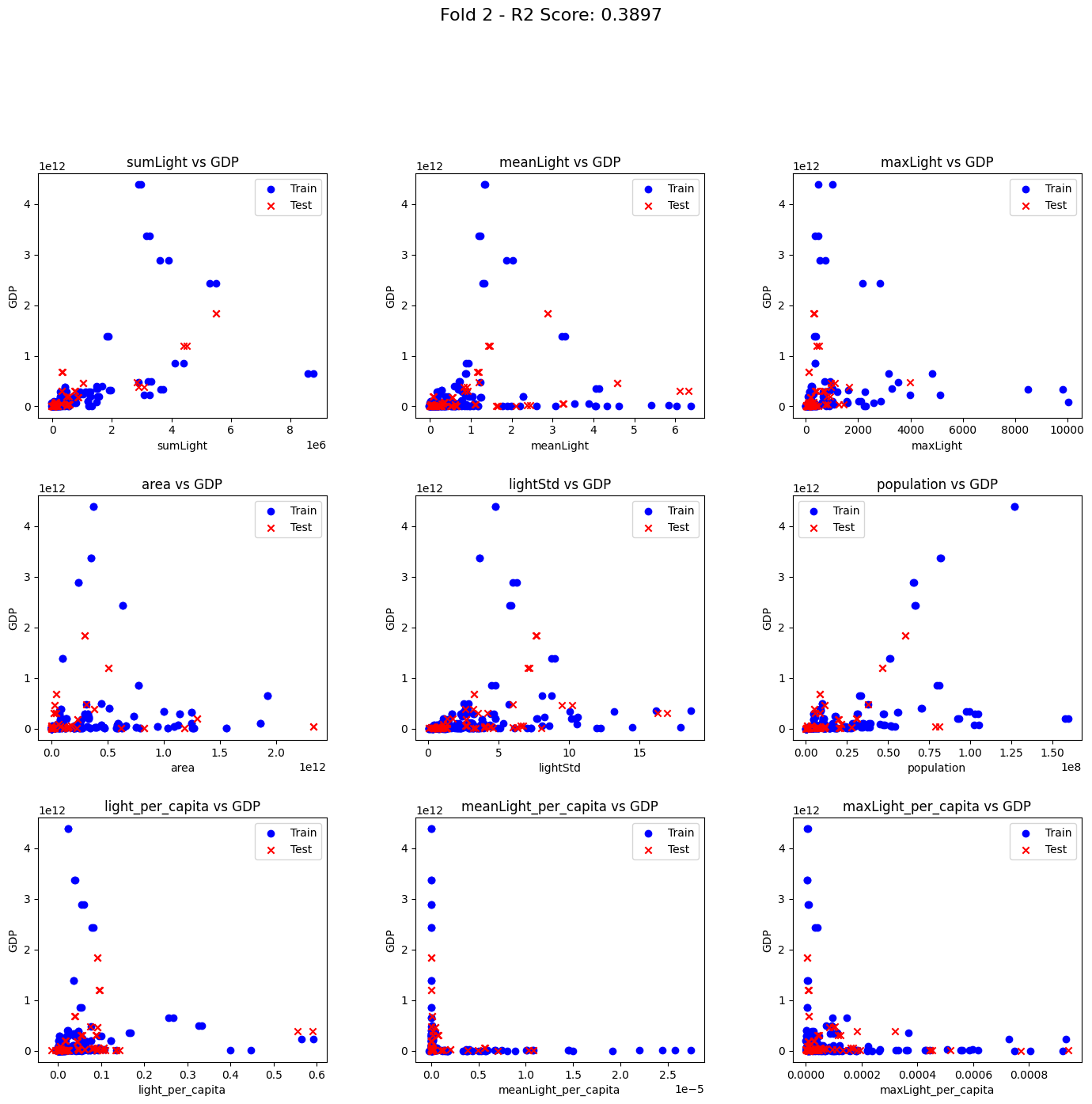
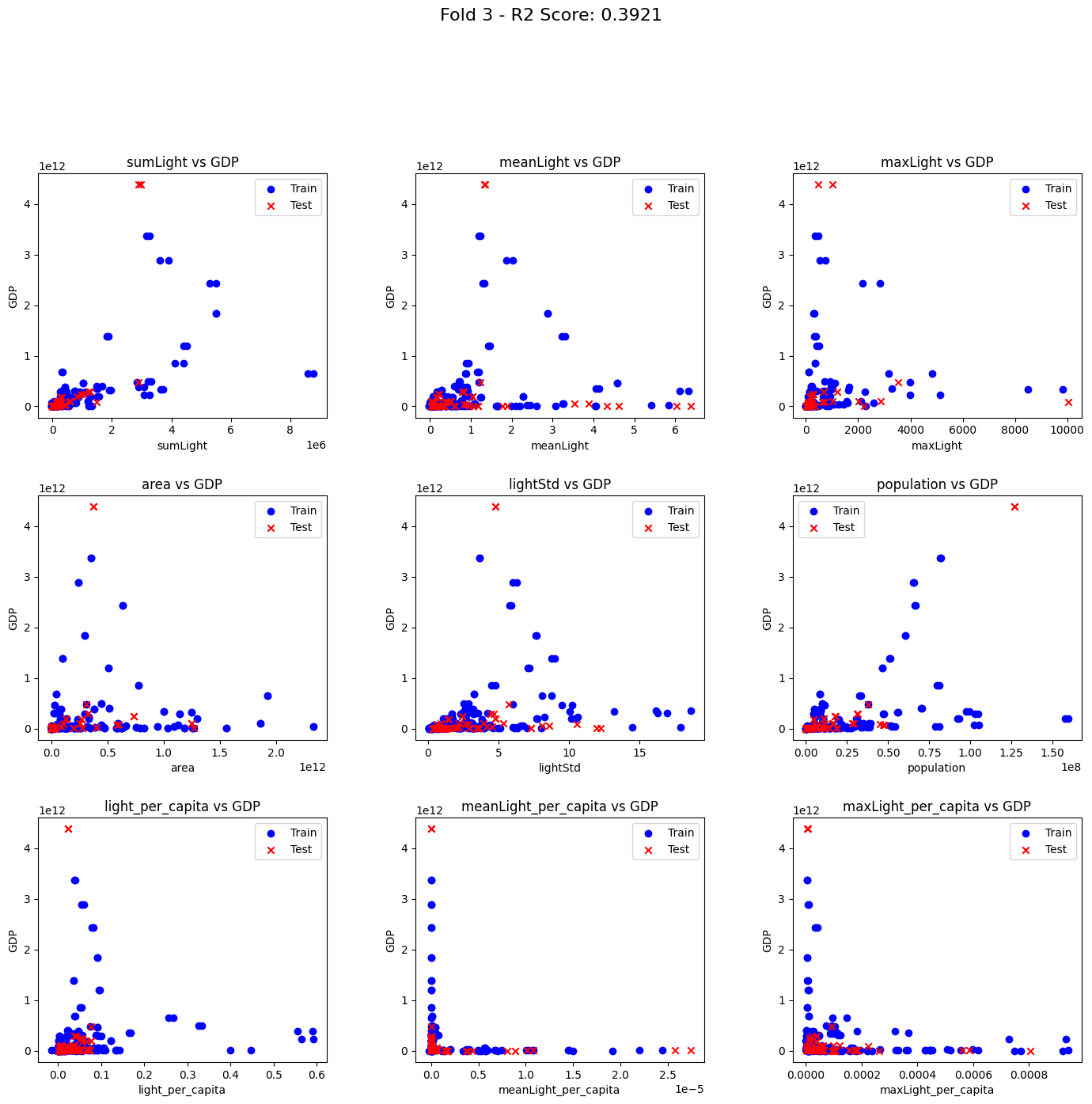
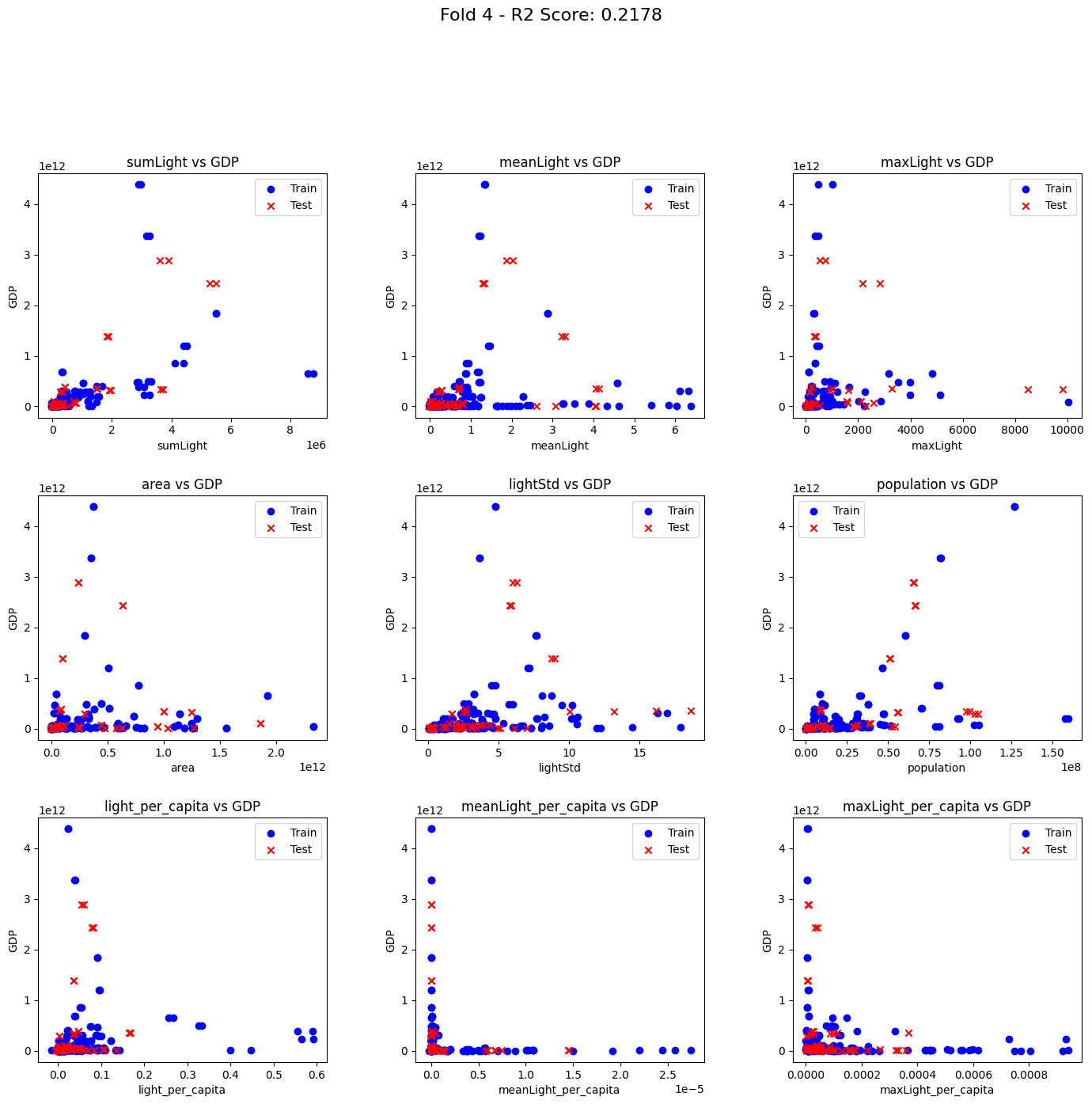
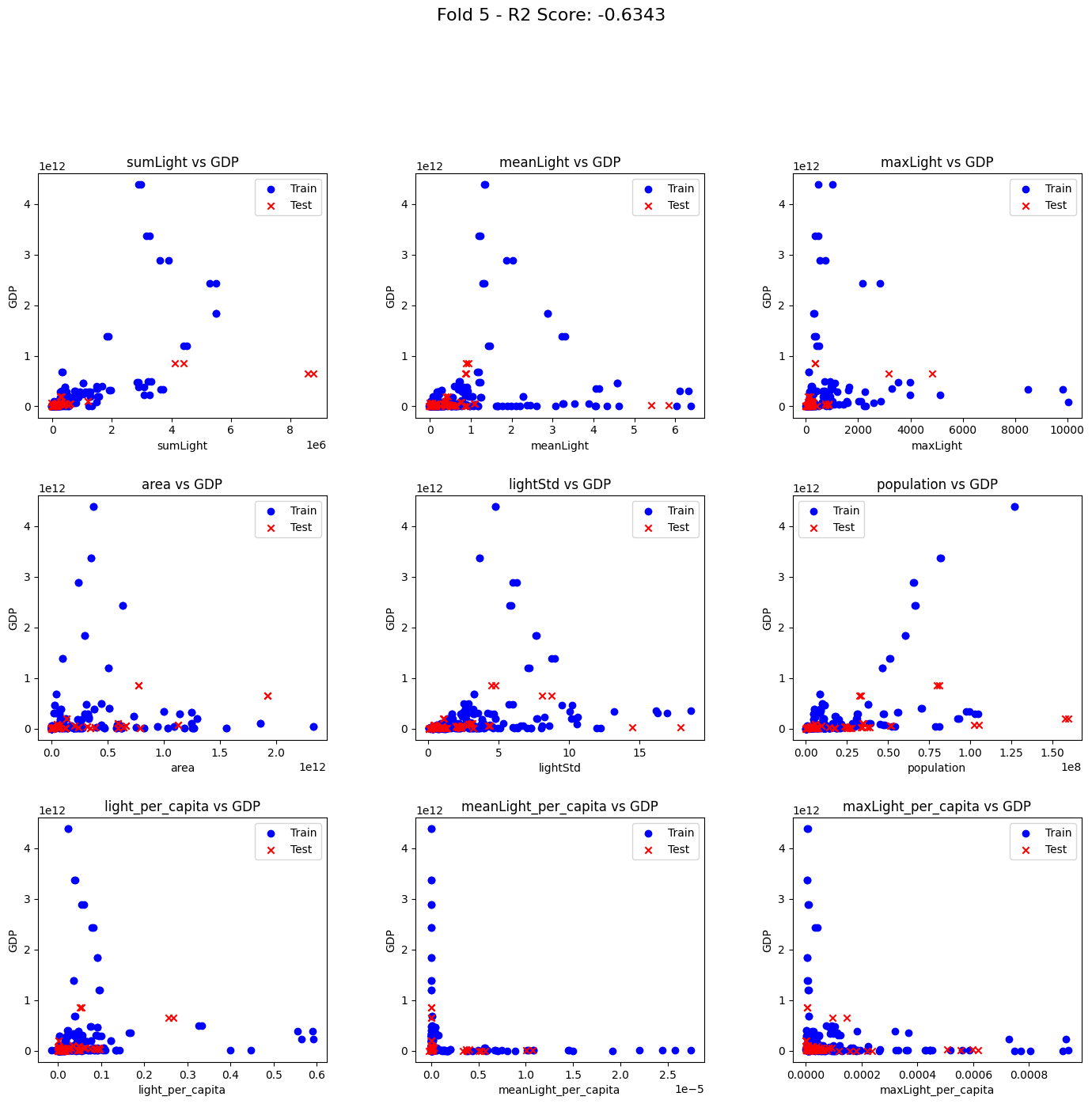
    plot_scatter(X_train, X_test, y_train, y_test, fold_num, r2)

print("R2 Scores:", r2_scores)

R2スコアは以下の通りでした。

R2 Scores: [0.7655388596362518, 0.38967869259752963, 0.39207152413234625, 0.21784932841126425, -0.6343433850304951]

各実行時のグラフ結果は以下でした。

2023/3/23
コメントにて、対数をとってみてはどうかとアドバイスをいただいたため両対数グラフを作成しました。
そのコードとグラフを記載します。

# @title 各特徴量とGDPとの散布図表示(両対数)

import seaborn as sns
import matplotlib.pyplot as plt

features = [col for col in dataset.columns if col not in ['country', 'year', 'GDP']]

fig, axes = plt.subplots(len(features) // 3 + len(features) % 3, 3, figsize=(15, 15))
fig.tight_layout(pad=5.0)

for ax, feature in zip(axes.ravel(), features):
    # sns.scatterplot(data=dataset, x=feature, y='GDP', ax=ax)
    ax.scatter(np.log10(dataset[feature]), np.log10(dataset['GDP']))
    ax.set_title(f'{feature} vs GDP')
    ax.set_xlabel(feature)
    ax.set_ylabel('GDP')

# 余分なサブプロットを非表示にする
for remaining_ax in axes.ravel()[len(features):]:
    remaining_ax.axis('off')

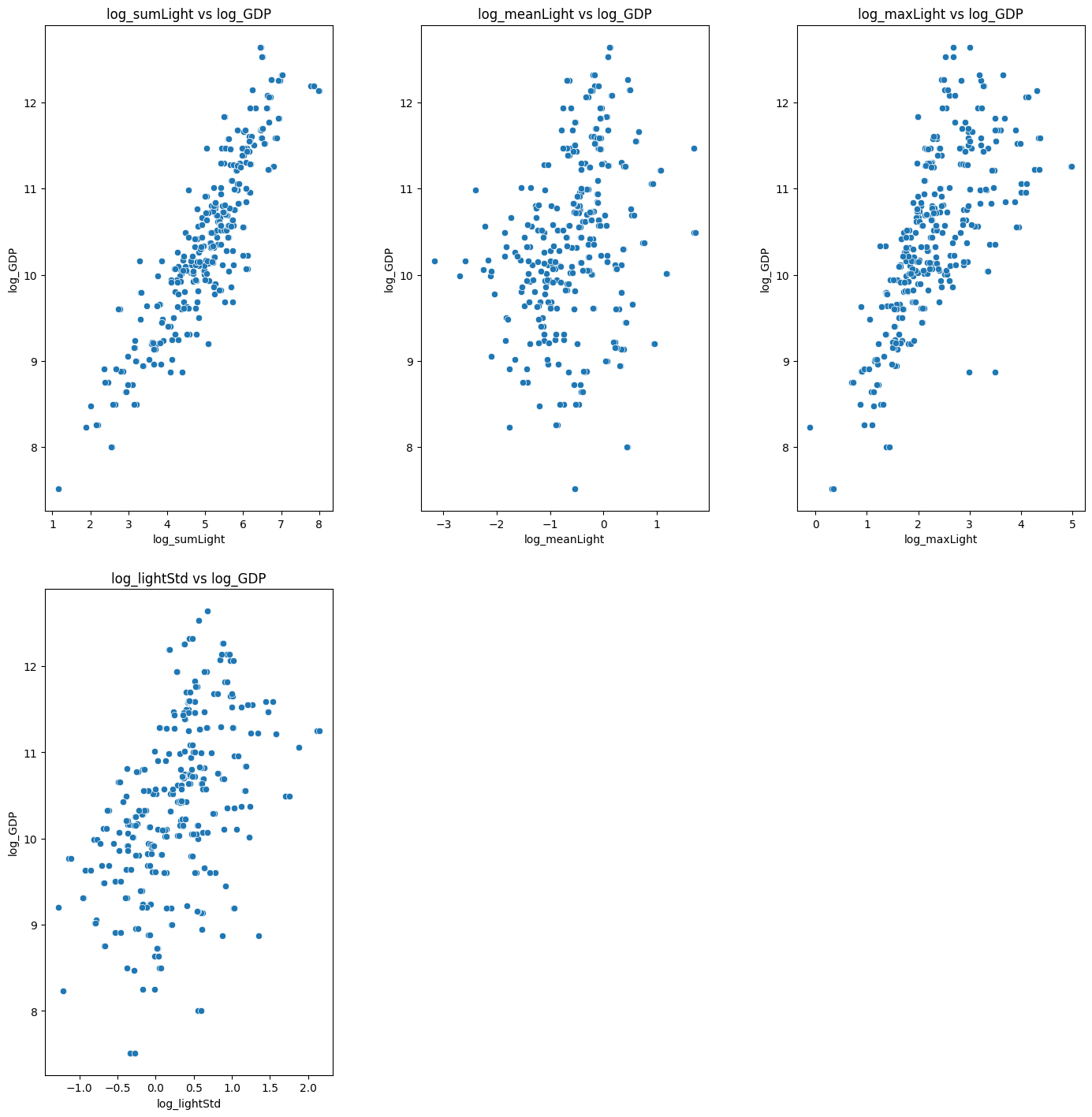
plt.show()

以下のような散布図になりました。
相関ありそうな特徴量が何個か出てきました。

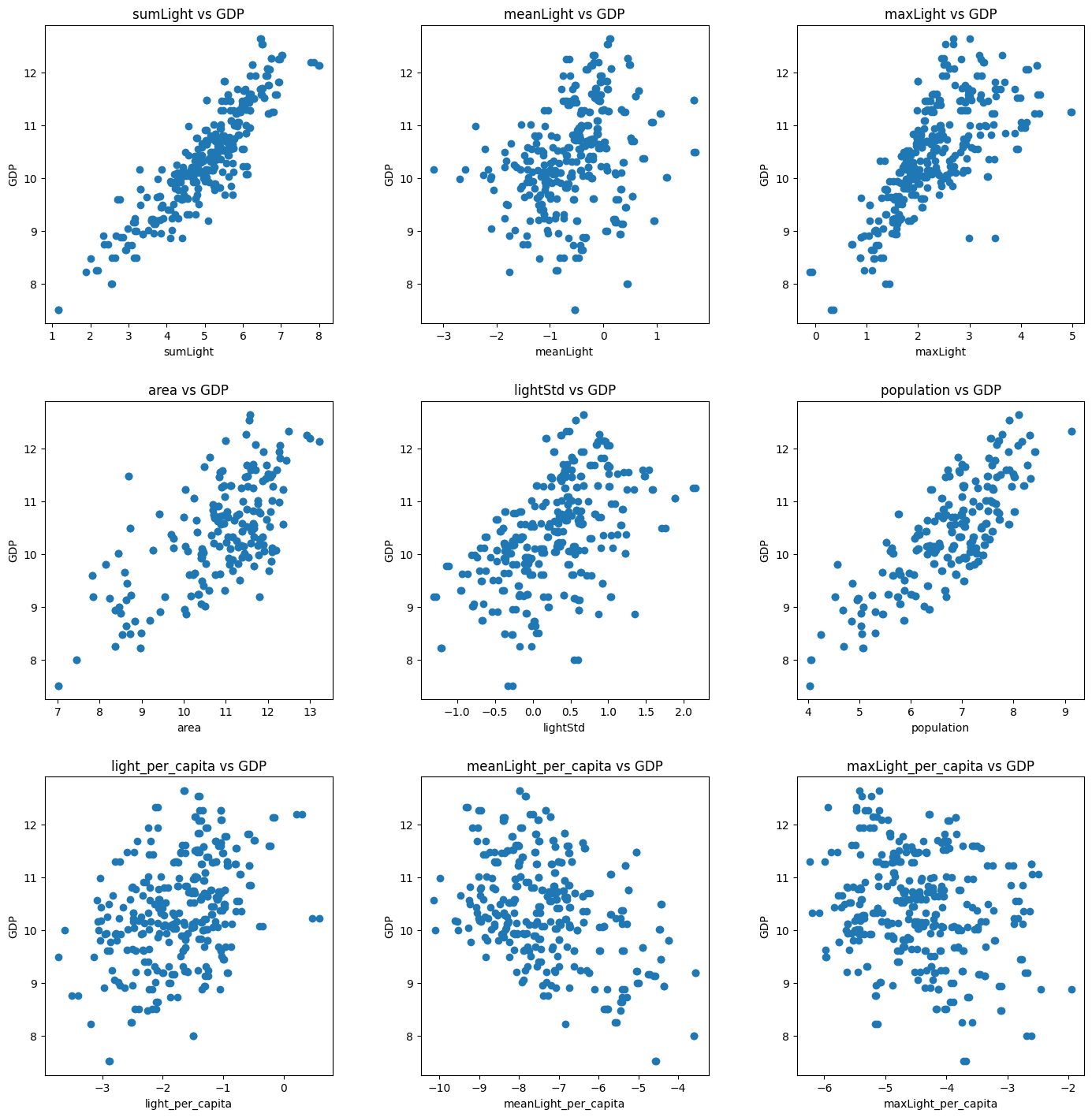
2023/3/23
上記にて両対数を取ると、相関値が上がりそうだということが見て取れたので、
改めて"sumLight", "meanLight", "maxLight", "lightStd"についての対数値を格納したデータセットを作成し、同じく機械学習を行っていきます。

import math

# Indexとなるカラム
index_columns = ["country", "year"]

# 対数を取りたいカラムのリスト
target_columns = ["GDP", "sumLight", "meanLight", "maxLight", "lightStd"]

log_dataset = dataset[index_columns + target_columns]
# 指定したカラムに対して対数を計算し、新しいカラムとして追加
for column in target_columns:
  log_dataset['log_' + column] = log_dataset[column].apply(lambda x: None if x <= 0 else math.log(x, 10))

# 「log_」を含むカラム名を選択
log_columns = [col for col in log_dataset.columns if 'log_' in col]

# 対数カラムのみ選択
log_dataset = log_dataset[index_columns + log_columns]

log_dataset.dropna(inplace=True)
log_dataset.reset_index(inplace=True, drop=True)
log_dataset

以下のような結果が取得、log_datasetに格納されます。

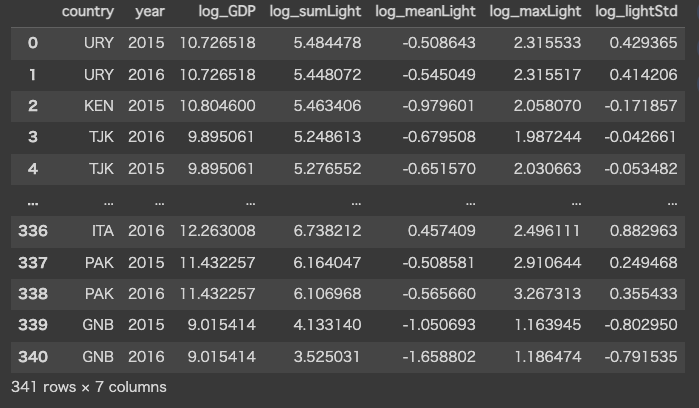
目立った外れ値は見て取れませんでしたが、前回の流れを踏襲しているため対数用のデータセットにも一応外れ値除外の処理を行っておきます。

# @title 対数処理後の外れ値除外

from scipy import stats
import numpy as np

features = [col for col in log_dataset.columns if col not in ['country', 'year', 'log_GDP']]

# オブジェクト型の列を数値型に変換
log_dataset[features] = log_dataset[features].apply(pd.to_numeric, errors='coerce')

# NaN（変換できなかった値）を除去
log_dataset.dropna(subset=features, inplace=True)

# Z-Scoreを計算(Z=(X-μ)/σ X:個々のデータ点, μ:データセットの平均, σ:標準偏差)
z_scores = np.abs(stats.zscore(log_dataset[features]))

# 閾値を設定（σと同義）
threshold = 1

# 外れ値を含まない行だけを抽出
log_dataset = log_dataset[(z_scores < threshold).all(axis=1)]

対数化及び外れ値除外後のデータセットのグラフ表示を行います。

# @title 各特徴量とGDPとの散布図表示(両対数&外れ値除外後)

import seaborn as sns
import matplotlib.pyplot as plt

features = [col for col in log_dataset.columns if col not in ['country', 'year', 'log_GDP']]

fig, axes = plt.subplots(len(features) // 3 + len(features) % 3, 3, figsize=(15, 15))
fig.tight_layout(pad=5.0)

for ax, feature in zip(axes.ravel(), features):
    sns.scatterplot(data=dataset, x=feature, y='log_GDP', ax=ax)
    ax.set_title(f'{feature} vs log_GDP')
    ax.set_xlabel(feature)
    ax.set_ylabel('log_GDP')

# 余分なサブプロットを非表示にする
for remaining_ax in axes.ravel()[len(features):]:
    remaining_ax.axis('off')

plt.show()

結果は以下のようなグラフになりました。

機械学習の実行(対数版)

ここからは対数化したあとのデータセットに対し、機械学習のモデル作成に入っていきます。
まずはトレーニング用のデータとテスト用のデータでデータセットを分けます。

from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score

# 特徴量とターゲットを分割
X = log_dataset.drop(columns=['country', 'year', 'log_GDP']).astype('float64')  # countryとyear,log_GDP以外のすべての列が特徴量
y = log_dataset['log_GDP'].astype('float64')

# データをトレーニングセットとテストセットに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

線形回帰モデル

from sklearn.linear_model import LinearRegression

# 線形回帰モデルの作成とトレーニング
lr_model = LinearRegression()
lr_model.fit(X_train, y_train)

# 線形回帰モデルの評価
y_pred_lr = lr_model.predict(X_test)
mse_lr = mean_squared_error(y_test, y_pred_lr)
r2_lr = r2_score(y_test, y_pred_lr)

# 評価結果を表示
print("LinearRegression Model:")
print(f"Mean Squared Error: {mse_lr}")
print(f"R^2 Score: {r2_lr}\n")

線形回帰モデルの結果は以下でした。

LinearRegression Model:
Mean Squared Error: 0.12115590511096085
R^2 Score: 0.7748934579331663

SVMモデル

from sklearn.svm import SVR

# SVMモデルの作成とトレーニング
svm_model = SVR()
svm_model.fit(X_train, y_train)

# SVMモデルの評価
y_pred_svm = svm_model.predict(X_test)
mse_lr = mean_squared_error(y_test, y_pred_svm)
r2_svm = r2_score(y_test, y_pred_svm)

# 評価結果を表示
print("SVM Model:")
print(f"Mean Squared Error: {mse_lr}")
print(f"R^2 Score: {r2_svm}\n")

SVMモデルの結果は以下でした。

SVM Model:
Mean Squared Error: 0.1490426687079703
R^2 Score: 0.7230801111795864

決定木モデル

from sklearn.tree import DecisionTreeRegressor

# 決定木モデルの作成とトレーニング
tree_model = DecisionTreeRegressor(random_state=42)
tree_model.fit(X_train, y_train)

# 決定木モデルの評価
y_pred_tree = tree_model.predict(X_test)
mse_tree = mean_squared_error(y_test, y_pred_tree)
r2_tree = r2_score(y_test, y_pred_tree)

# 評価結果を表示
print("Decision Tree Model:")
print(f"Mean Squared Error: {mse_tree}")
print(f"R^2 Score: {r2_tree}\n")

決定木モデルの結果は以下でした。

Decision Tree Model:
Mean Squared Error: 0.22104224019174043
R^2 Score: 0.5893055786699116

ランダムフォレストモデル

from sklearn.ensemble import RandomForestRegressor

# ランダムフォレストモデルの作成とトレーニング
forest_model = RandomForestRegressor(random_state=42)
forest_model.fit(X_train, y_train)

# ランダムフォレストモデルの評価
y_pred_forest = forest_model.predict(X_test)
mse_forest = mean_squared_error(y_test, y_pred_forest)
r2_forest = r2_score(y_test, y_pred_forest)

# 評価結果を表示
print("Random Forest Model:")
print(f"Mean Squared Error: {mse_forest}")
print(f"R^2 Score: {r2_forest}")

ランダムフォレストモデルの結果は以下でした。

Random Forest Model:
Mean Squared Error: 0.12471118274489718
R^2 Score: 0.7682877852378901

LightGBM(Light Gradient Boosting Machine)モデル

import lightgbm as lgb

# データセットの作成
train_data = lgb.Dataset(X_train, label=y_train)
test_data = lgb.Dataset(X_test, label=y_test, reference=train_data)

# パラメータの設定
params = {
    'boosting_type': 'gbdt',
    'objective': 'regression',
    'metric': {'l2', 'l1'},
    'num_leaves': 31,
    'learning_rate': 0.05,
    'feature_fraction': 0.9,
    'bagging_fraction': 0.8,
    'bagging_freq': 5,
    'verbose': 0
}

# モデルのトレーニング
num_round = 100
lgbm_model = lgb.train(
    params,
    train_data,
    num_round,
    valid_sets=[test_data],
    callbacks=[lgb.early_stopping(stopping_rounds=10)]
)

# 予測
y_pred_lgbm = lgbm_model.predict(X_test, num_iteration=lgbm_model.best_iteration)

# 評価
mse_lgbm = mean_squared_error(y_test, y_pred_lgbm)
r2_lgbm = r2_score(y_test, y_pred_lgbm)

# 評価結果を表示
print("LightGBM Model:")
print(f"Mean Squared Error: {mse_lgbm}")
print(f"R^2 Score: {r2_lgbm}")

LightGBMモデルの結果は以下でした。

LightGBM Model:
Mean Squared Error: 0.16644226160488101
R^2 Score: 0.6907518298068622

ニューラルネットワークモデル

from sklearn.neural_network import MLPRegressor
from sklearn.model_selection import GridSearchCV

# パラメータのグリッドを定義
param_grid = {
    'hidden_layer_sizes': [(100, 50), (50, 25), (100,)],
    'activation': ['tanh', 'relu'],
    'solver': ['sgd', 'adam'],
    'alpha': [0.0001, 0.001, 0.01],
    'learning_rate': ['constant', 'adaptive']
}

# MLPRegressor のインスタンスを作成
mlp = MLPRegressor(max_iter=1000)

# GridSearchCV のインスタンスを作成
grid_search = GridSearchCV(mlp, param_grid, cv=3, scoring='neg_mean_squared_error', n_jobs=-1)

# グリッドサーチを実行
grid_search.fit(X_train, y_train)

# 最適なハイパーパラメータを表示
print("Best Hyperparameters:", grid_search.best_params_)

# 最適なモデルで評価
best_mlp = grid_search.best_estimator_
y_pred = best_mlp.predict(X_test)

# 評価
rmse = np.sqrt(mean_squared_error(y_test, y_pred))
r2_score = r2_score(y_test, y_pred)
print(f"Test RMSE with Neural Network: {rmse}")
print(f"Test R2SCORE with Neural Network: {r2_score}")

ニューラルネットワークモデルの結果は以下でした。

Test RMSE with Neural Network: 0.5755473893727725
Test R2SCORE with Neural Network: 0.384531674947414

対数化の前後で大幅にスコアが向上しました。
アドバイスいただいた方に感謝しております。

まとめ

ランダムフォレストでのフィッテングであれば、そこそこの結果を得られました。
しかしクロスバリデーションを行うとランダムフォレストであってもスコアは非常に悪くなりました。（一応他も試しましたが軒のみ低いです。)今回のクロスバーリデーションはK分割交差法を採用していますが、元々トレーニングデータが少なかったため、更に少ないデータに分割し交差検証を行うと各々で過学習が発生してしまったのではないかと考えています。
データを増やすことと、交差検証方法についてはまだ勉強が必要なようですが、ひとまず欲しいデータ（今回の場合夜間光や人口データ）を取得し、それらをデータセット化した後トレーニングデータとテストデータに分けモデル構築していくという一連の流れは実施できたと思います。なにか勘違いしていることやこうした方がいいなどのコメントございましたら歓迎いたします。

2023/3/23
コメントにてアドバイスを頂き、測定し直した結果大幅にスコアが向上しました。クロスバリデーションしてもマイナス値を取ることはないことを確認できています。
データレンジが大きい際は対数化してみるということと、やはり使用データの準備・整理がいかに重要化を再認識いたしました。
コメントいただいた方に改めて感謝申し上げます。