Deep Walkとは
スキップグラム
自然言語処理の分野で用いられる、1つの単語は複数の意味をもつと、いった理論をもとに提案されました。そもそもスキップグラムは周辺の単語を用いて単語そのものの表現を学習するというものです。
例)
1.This light is good.
2.This bag is light
ここで[light]は同じlightでも「ライト」と「軽い」という2つの意味を持ちます。これは前後の文を見れば一目瞭然でどちらがどちらの意味か分かります。このように、周辺の単語を用いてその単語の表現を学習する手法がスキップグラムです。
Deep Walk概要
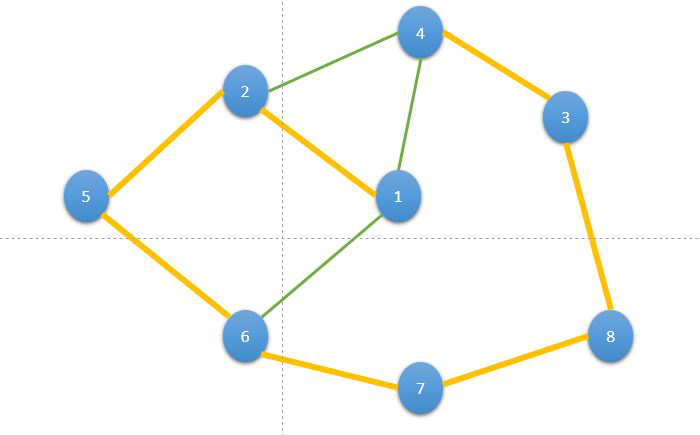
参考文献[https://acervolima.com/deepwalk-algorithm/]
グラフも単語だと捉えて、スキップグラムの考え方を応用することができます。
This is a pen.
ノード1 ノード2 ノード3 ノード4
といったように、順番に歩く(Walk)するようにたどれば単語と同じような意味合いで解釈することができます。
Deep Walk 詳しく
ここでの頂点の列を以下のようにあらわします。
$$w_1, w_2,...,w_L\in V$$
ランダムでWalkしているときに通過する頂点を$$Z_i \in R^d$$と表すようにします。ランダムWalkしている途中に、頂点vが頂点uの前後Tステップ以内に登場する確率を以下のようにあらわします。
$$p_\theta(v|u) = \frac{\exp(Z_u^TZ_v)}{\Sigma_{k \in V}\exp(Z_u^TZ_k)}$$
難しそうな式に見えナンスが、頂点uが通ったときに頂点vが通った確率の式です。Tは前後ステップではなく転置です。ここで式がexpをとり、ソフトマックスのようになっているのは大規模なグラフでは計算に時間がかかりすぎるためです。
よって最適化する目的関数はここの確率が合うように学習します。つまり、実際に頂点vがTステップ内に頂点uを通った確率と、表現学習によって学習された確率が等しくなるように学習するというわけです。
ここで確率分布を一致させるのですから、目的関数にはKLダイバージェンスが用いられます。
$$-E_{u~p(u)}[KL(p^*(v|u) || p_\theta (v|u))]+const.$$
実際の確率分布pと予測の確率分布p*の分布を近づけるように学習します。
参考文献
書籍:グラフニューラルネットワーク ・佐藤 竜馬