はじめに
「もっと細かくサンプリングしたいけど、ハードのスペックが足りない！😣」
「一部だけロギング失敗しちゃった！またデータ取り直し！？😨」
こんな経験、ありませんか？私はあります。
こんな時って、データ取りの条件を妥協したり、もう一回セッティング&データ取りをやり直したり大変ですよね。
でも、もし今手元にあるデータから思い通りのデータを生み出すことができたら？
それもただの補間ではなく、きちんと手元にあるデータの構造を元に、それに沿ったデータを作ることができたら？
まるで魔術ですが、ある数学的な道具を使うことで、魔術を技術にすることができます。
というわけで、本記事はデータの復元技術である「信号復元」について、数学的な説明は一旦脇に置いておいて、何ができるかを見て、体験してもらうことを目的にしています。
記事を読んでコードを動かすことで「こんなことができるんだ！」と、驚きと面白さを感じてもらうことができるはずです。
また、もしご興味があれば数学的な道具の説明をzennに投稿しているので、そちらを参照して頂ければと思います。
本記事による体験と上記リンク記事による理解により、胸を張って、
「データが取れてない？なら復元すれば良いじゃない！」 と言ってもらえれば嬉しいです。
まずはやってみよう！
信号復元で一体何がどうなるの？ということで、早速信号復元の様子をデモで示します。
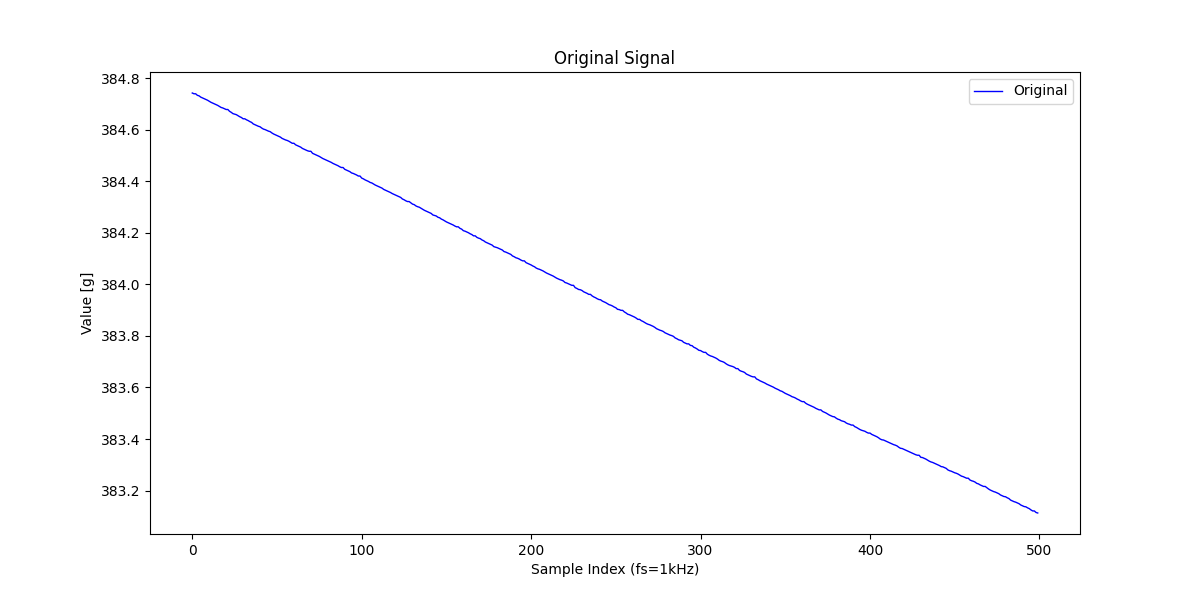
こんな感じの元信号(真の信号)を使います。
※余談ですが、これはロスインウェイト方式のパーツフィーダから取得した重量データで、
縦軸の単位が[g]なのはそれが理由です。
・真の信号(元信号)
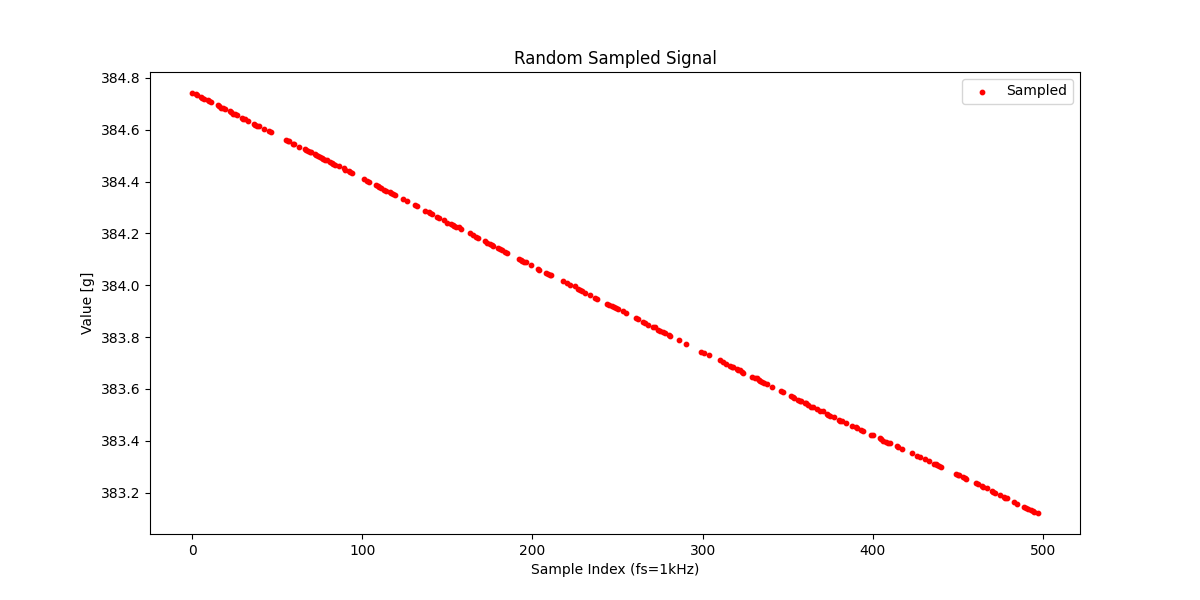
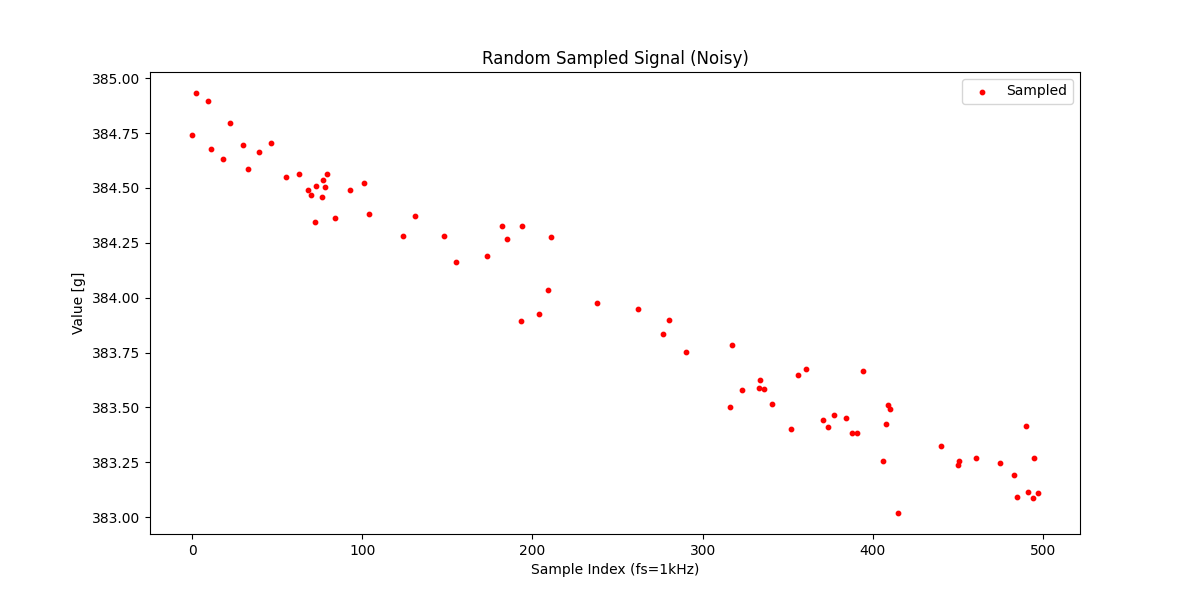
半分が欠損データだと想定して、元信号からランダムにサンプリングします。
・50%ランダムサンプリング結果
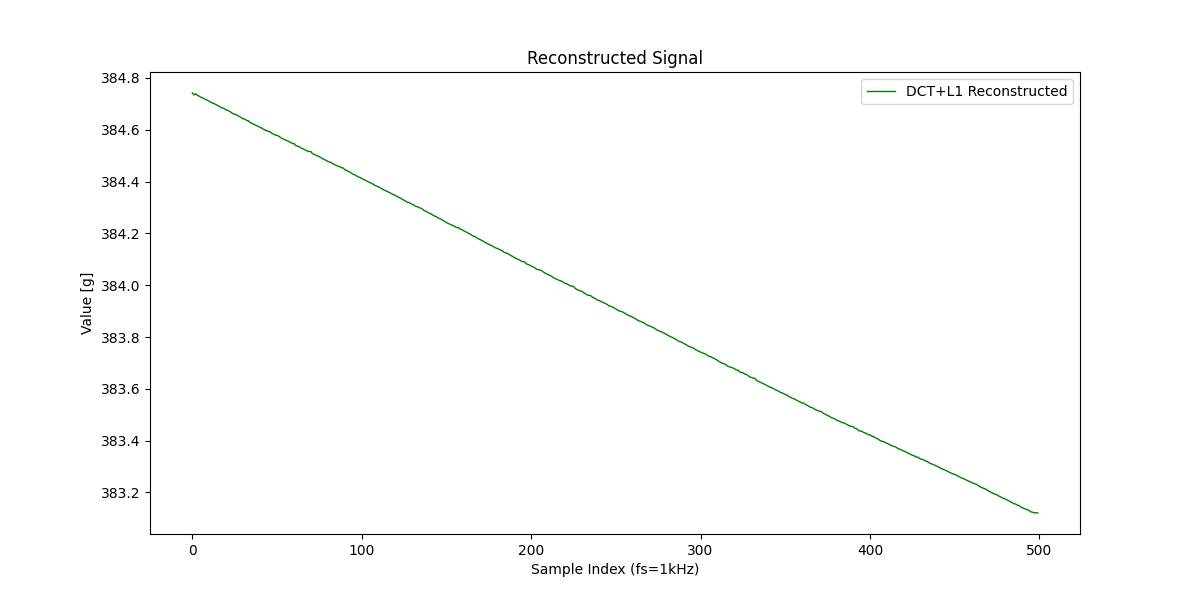
欠損データを元に信号を復元します
・復元信号
元信号との比較です。
・元信号vs復元信号
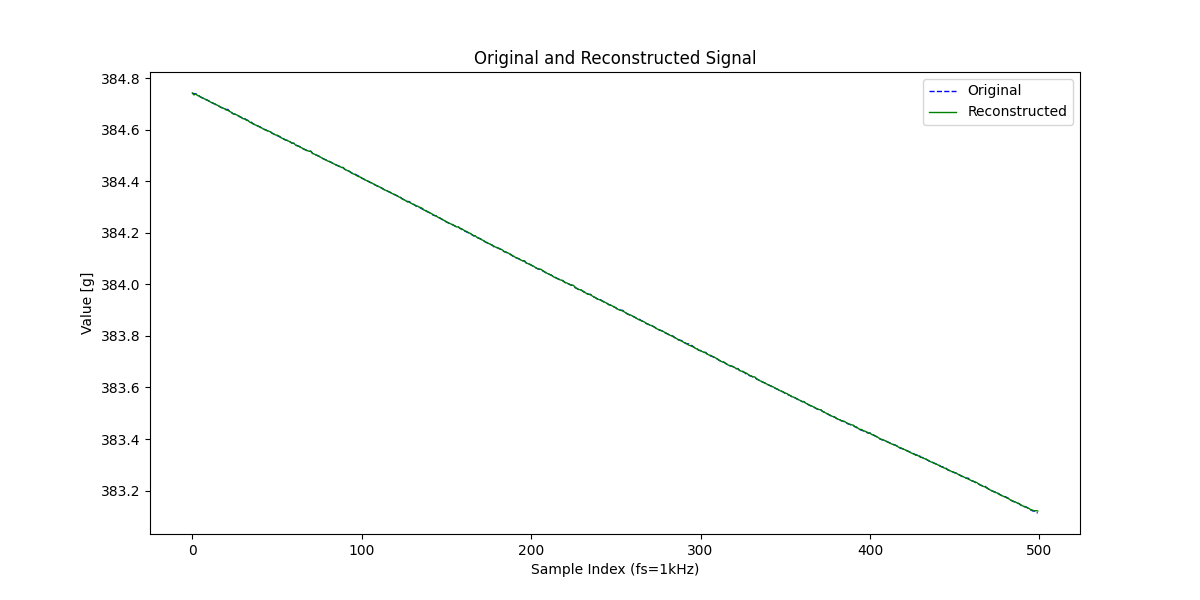
※MSE(平均二乗誤差)は0.000001程度でした。ほぼ元信号とイコールですね。
さて、キレイに復元できていますよね？
ですが、今の場合だと全体の半分は正しくサンプリングできています。
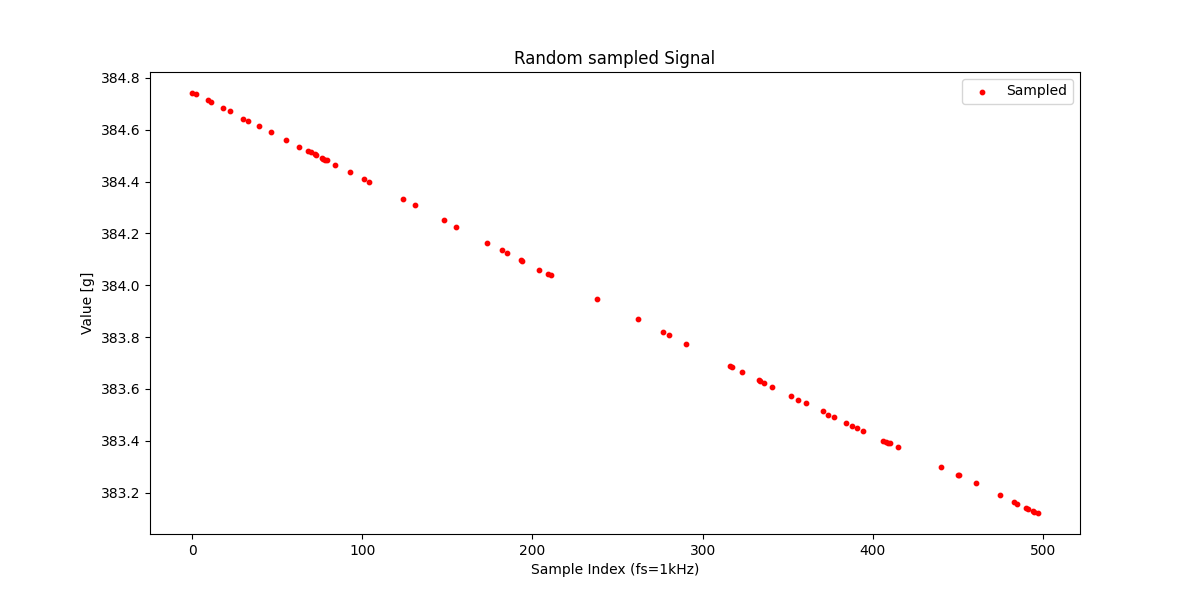
それでは、もっと欠損が大きく、たとえば全体の15%しか正しくサンプリングできていなかったとしたら、復元できるでしょうか？
・15%ランダムサンプリング結果
・元信号vs復元信号(その2)
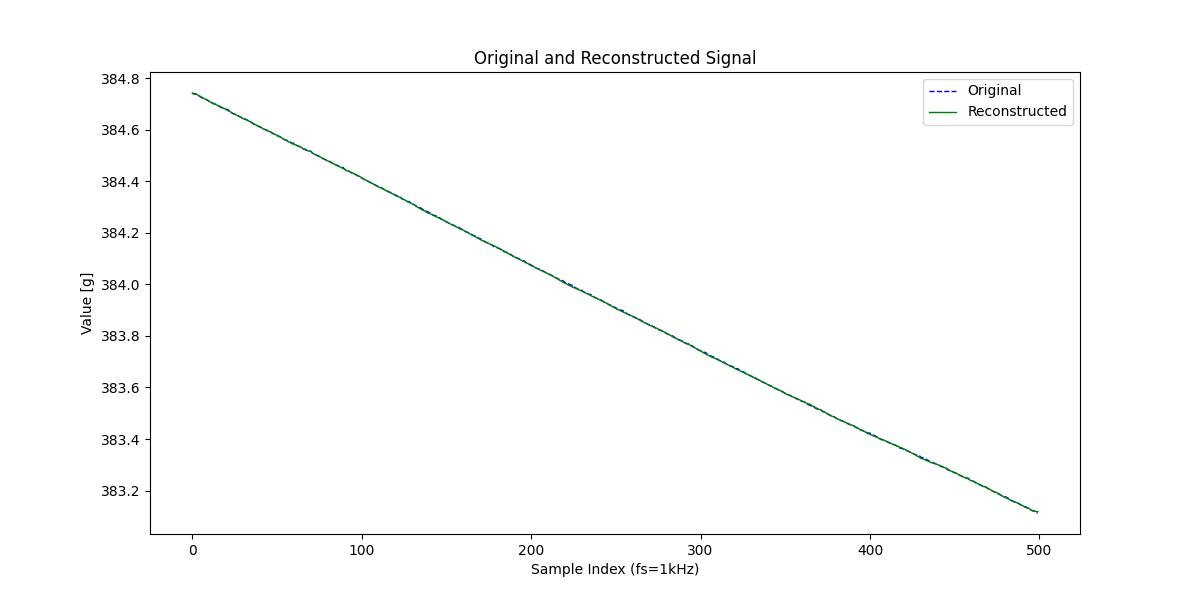
※MSEは0.000003程度です。やっぱり、ほぼ元信号とイコールですね。
どうでしょう、結構キレイだと思いませんか？
ここで肝心なことですが、15%しか正しくサンプリングできていないということは85%、
すなわち半分以上の信号は取得できていないということです。
それにもかかわらずこれだけの精度で復元できるなら、この信号復元という技術はいわゆるサンプリング定理で示される限界を突破できる可能性を秘めていると言って良いはずです。
補間じゃダメなんでしょうか？
と、ここまで信号復元を褒めてきましたが、素朴な疑問としてこんなのが浮かびませんか？
「それって線形補間とか、スプライン補間でも同じことできるんじゃないの？🤔」
答えは、ノーです！というか、イエスならこの記事はここで終わってしまいます！
誤解を恐れずに言うならば、補間は「手品」、信号復元は「魔術」 というぐらい違います。
※補間自体は素晴らしく役立つものです。私も補間にはよくお世話になっています。
が、すみません、ここではあえて悪いように言っています。
百聞は一見に如かず、やってみましょう。
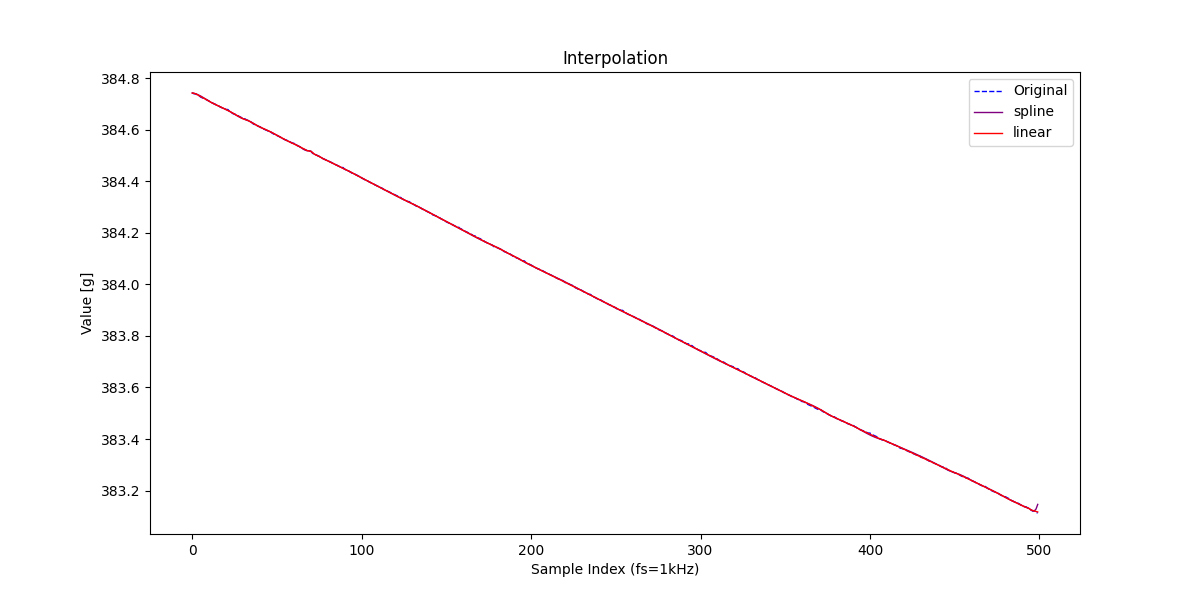
先ほど用いた、15%のみサンプリングした信号を線形補間とスプライン補間の両手法を用いて補間してみます。
・15%ランダムサンプリング結果
・線形補間及びスプライン補間結果
おっと、バッチリ補間できていますね。
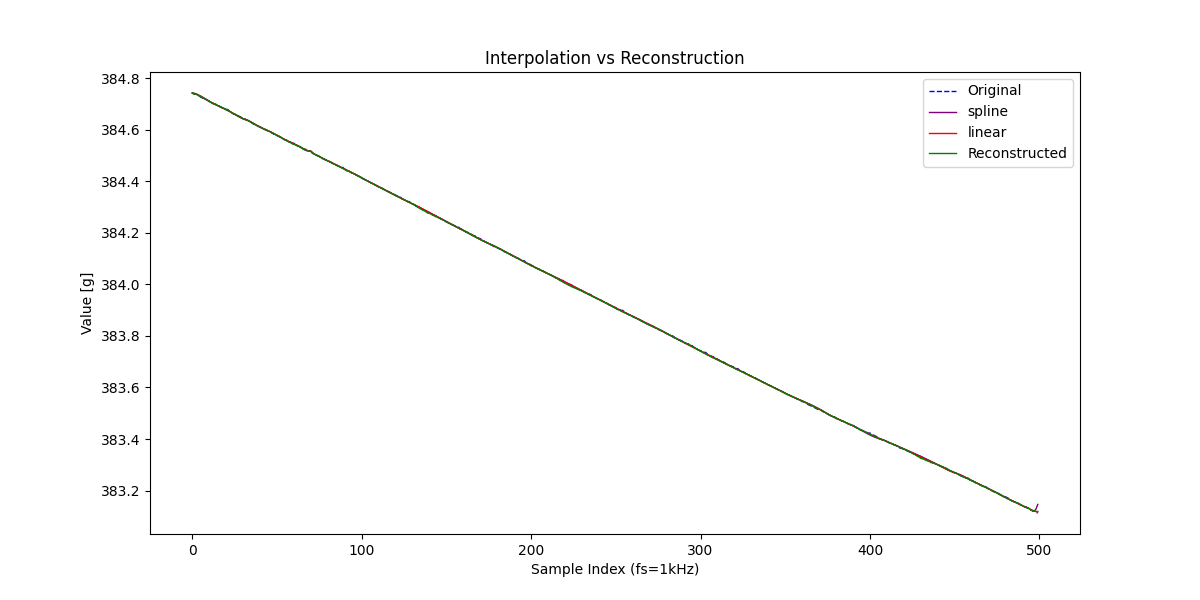
信号復元の手法で復元した結果と並べてみてもこの通りです。
・線形補間及びスプライン補間結果vs信号復元
さて、ここまでは補間も復元も結果は大差ありません。
しかし、次節で補間があくまで手品であり、真の魔術たりえないことを示します！
煩わしきもの、汝の名はノイズ
前節ではほぼ直線でノイズのほとんど重畳していない信号からランダムに15%サンプリングし、線形・スプライン補間と信号復元をそれぞれやってみました。
その結果、どのやり方でも同じように元の信号を補間または復元することができました。
しかし、実際に現場で取得するデータには当然ノイズがのっていますよね。
「前処理でフィルタリングすれば良いじゃん！」というのも一理ありますが、データに欠損があるとディジタルフィルタの仕様を決めるのもなかなか難しい側面があります。
なので、できれば取得データの欠損を補間・復元⇒揃ったデータに対してフィルタを設計
のような流れに沿って作業できればスムーズです。
つまりこの場合、ノイズの重畳した波形でも精度良く補間または復元できるか？ というのが両者の大事な評価ポイントになってくるわけです。
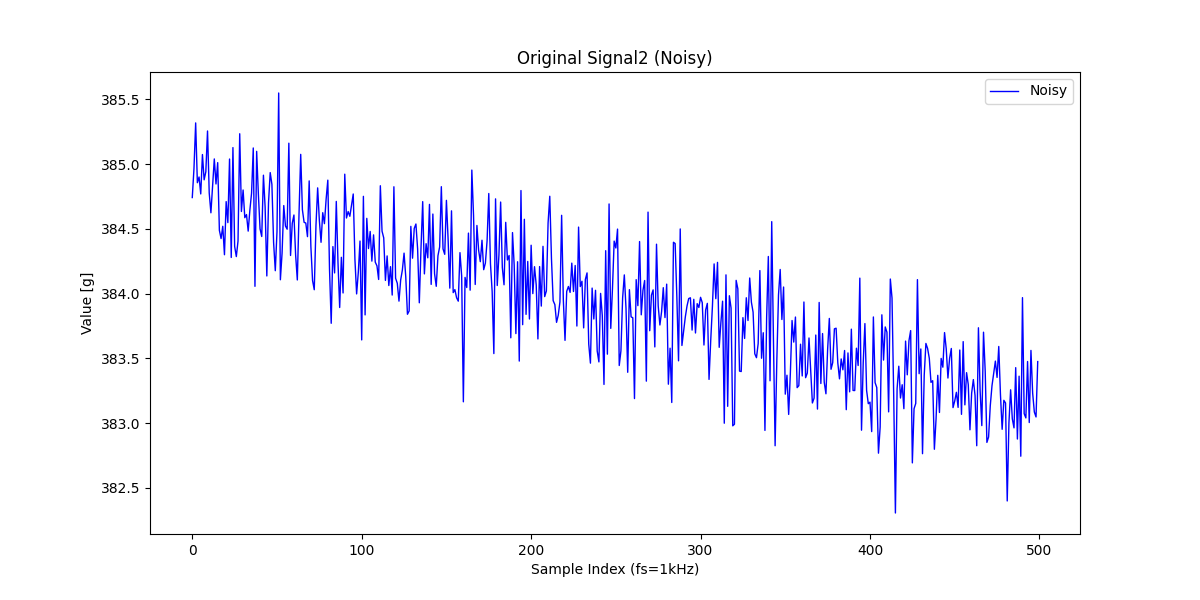
では早速、ノイズの重畳した波形にご登場願いましょう。
・ノイズ重畳信号
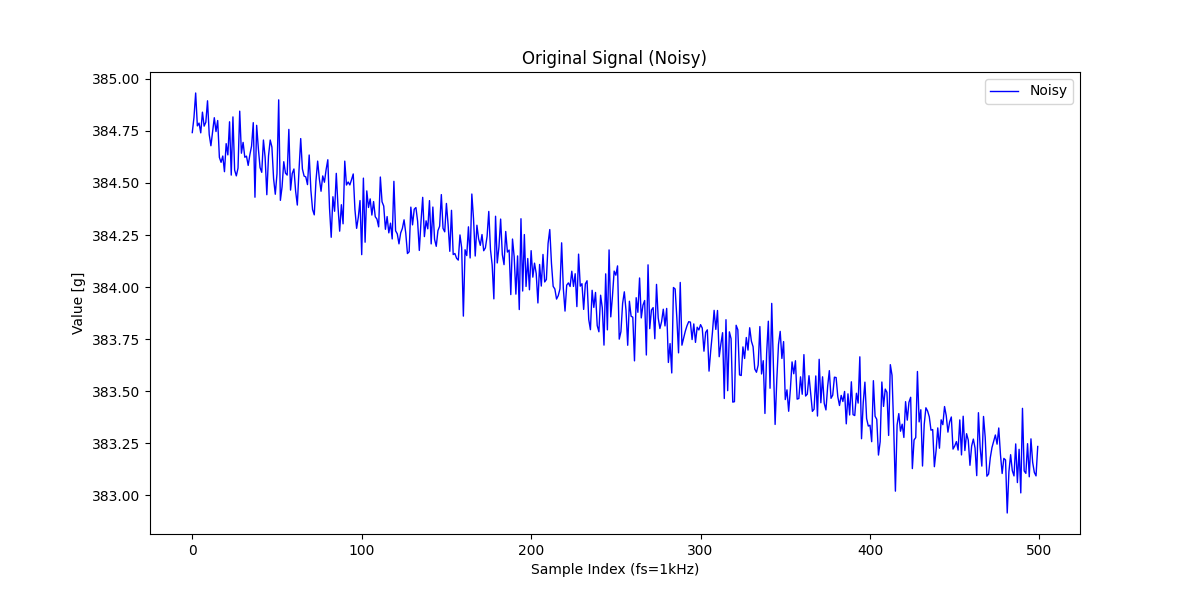
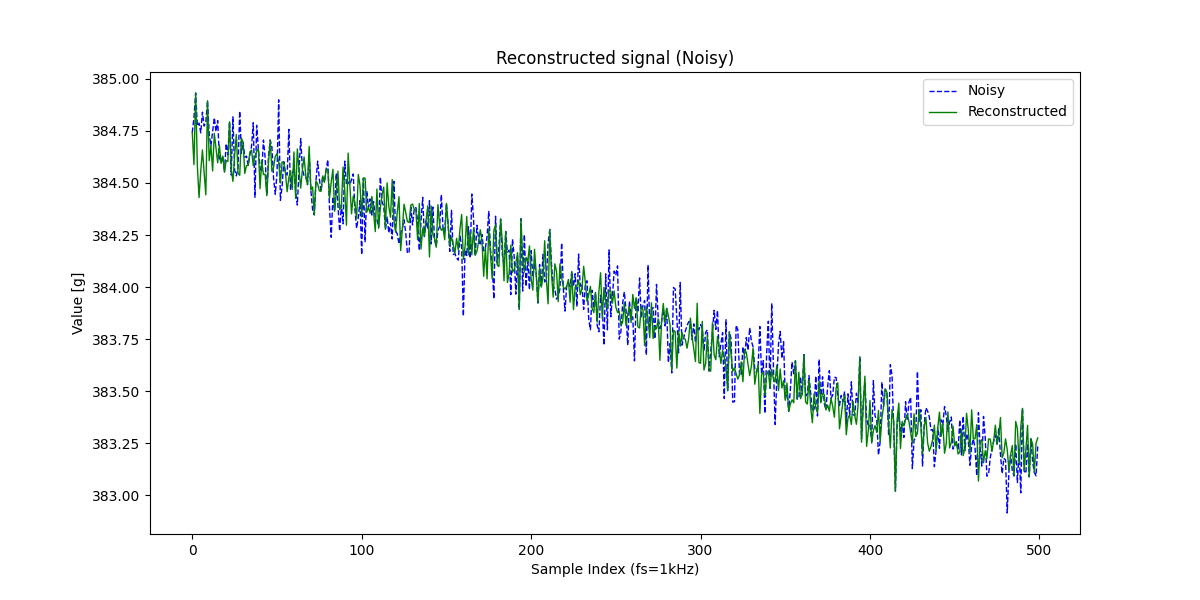
こんな感じで元信号に若干ガウスノイズをかぶせてみました。この信号に対して、同様に15%サンプリングして補間&復元をやっていきます。
・ノイズ重畳信号の15%ランダムサンプリング結果
・ノイズ重畳信号の復元信号
・ノイズ重畳信号の線形補間信号
・ノイズ重畳信号のスプライン補間信号
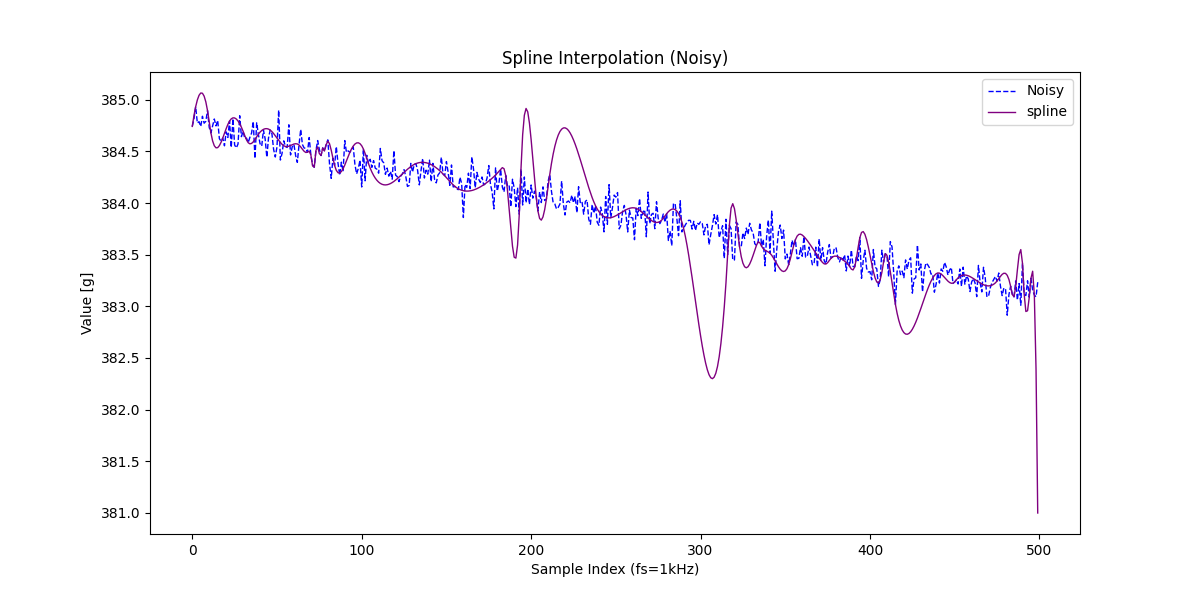
スプライン補間は論外ですね。全く実際のデータにフィットしていません。
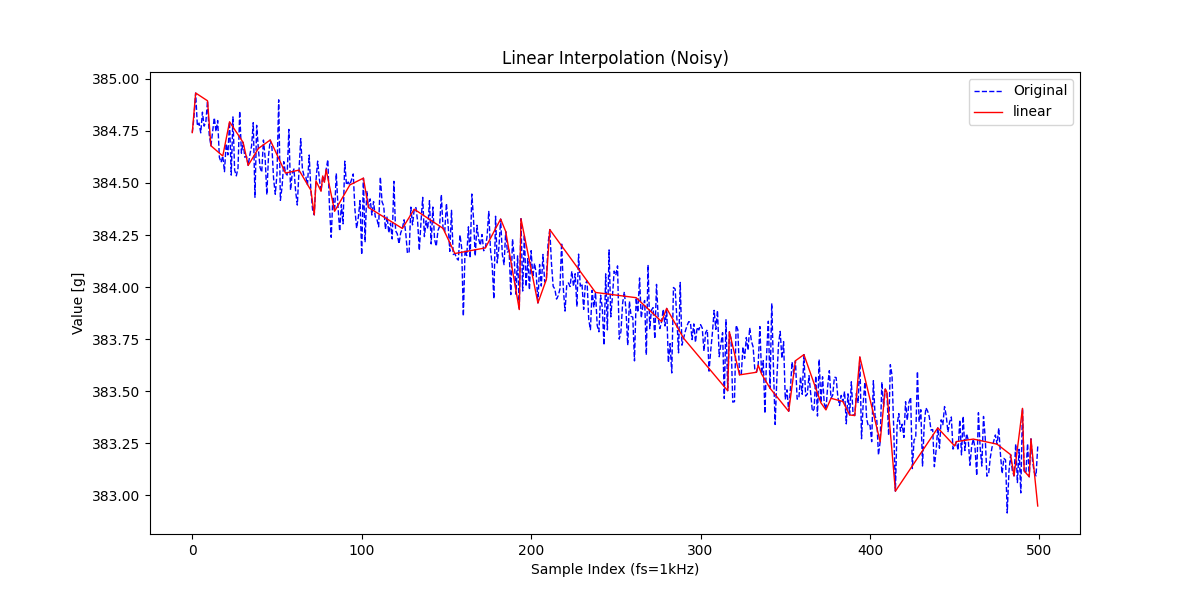
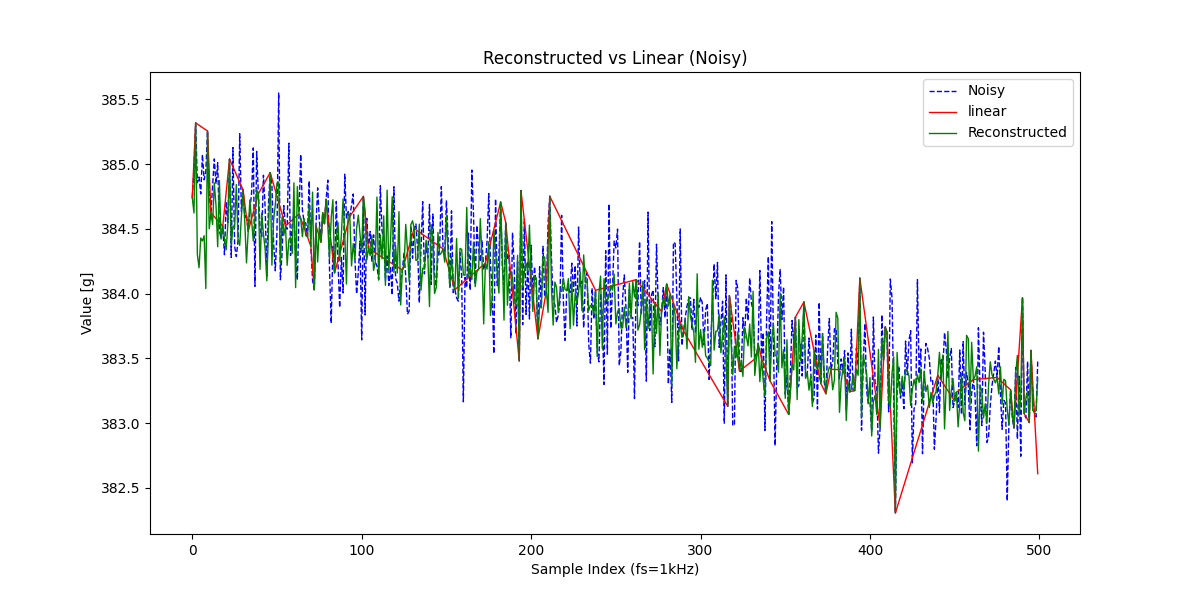
線形補間はそこそこ補間してくれていますが、信号復元よりスカスカで情報量が少なそうに見えますね。もう少し詳しく見てみましょう。
結果を見やすくするため、さきほどより少しノイズを強くしてみました。15%サンプリングして線形補間と信号復元の結果を比較してみます。
・ノイズ重畳信号(その2)
・ノイズ重畳信号(その2)の復元信号vs線形補間
中間部分(140~360サンプルの辺り)をアップにするともっと良く分かります。
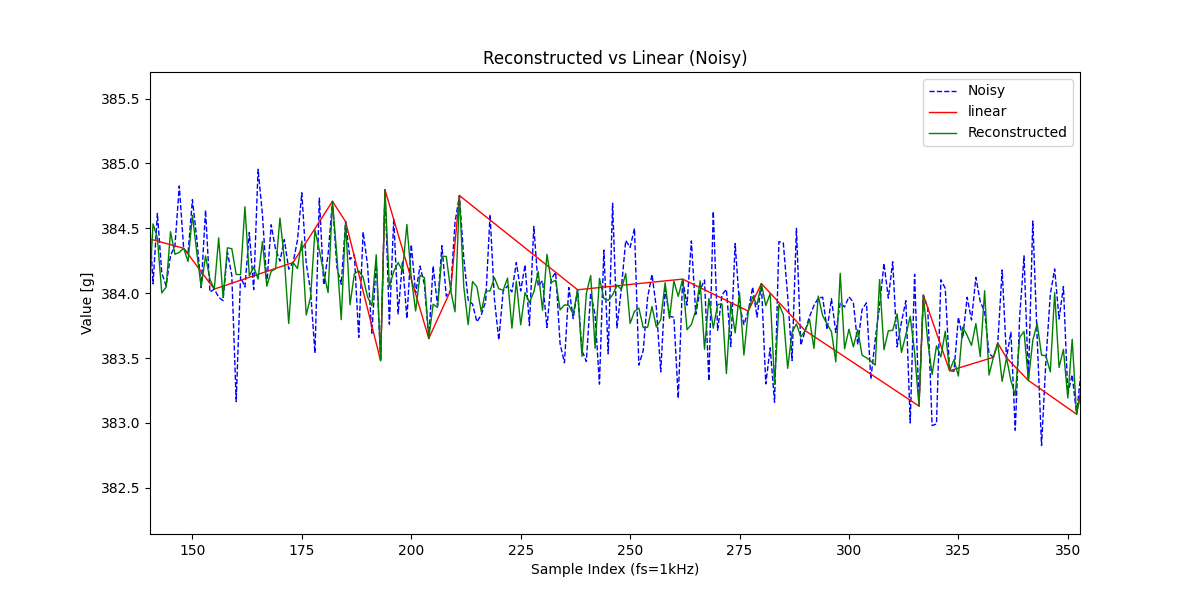
やはり線形補間による結果では元信号の情報がかなり落ちているように見えます。
実際に先程の信号復元vs線形補間vsスプライン補間のMSE(平均二乗誤差)を求めてみると、
信号復元(0.016) < 線形補間(0.018) < スプライン補間(0.119) となり、信号復元による結果が最も元信号との誤差が小さいと言えます。
この差はどうして生まれたのでしょうか？それぞれの手法をひとことで言うと、
信号復元：サンプリング点から元の信号のデータ構造を解析・復元する
信号補間：サンプリング点の間をそれっぽく直線・曲線で繋ぐ
どうでしょう？どちらが元信号の再現能力が高いと思いますか？
このことから信号復元と信号補間は根本的に考え方が異なるもので、先に述べた通り両者は魔術と手品ぐらいの差があると言えます。
まとめとGUIデモの使用方法
今回使用したデモコードは下記Githubに置いています(Python3.11で動作確認)
https://github.com/otter1602/Signal_Reconstruction_Demo
上記デモコードを動かすと、下記のようなGUIでデモアプリケーションが立ち上がります。
GUIデモの使用方法
ガウスノイズ振幅は0から設定可能で、0を設定するとノイズ無しの波形になります。
本記事では最初のノイズ有り信号で振幅は0.1、次が0.2で動作させていました。
また、データ保持率はランダムサンプリングで取得するサンプル数の割合を指定します。
記事中では0.5と0.15で動作させており、例えば0.15にすると全体の15%のみサンプリングを行うのですなわち85%の欠損ということになります。
線形補間と比較、スプライン補間と比較をチェックすると、結果画面に線形補間またはスプライン補間の結果を併せて表示します。
まとめ
本記事では信号復元でできること、補間との違いについて結果ベースで述べてきました。
信号復元の手法を用いることでサンプリング定理の壁を突破できること、そして補間との違いで述べたように、データ構造を保ったまま信号を復元できることを何となく雰囲気でも掴んでもらえれば嬉しいです。
Githubのリポジトリ内に記事中で使用していた真の信号をcsv形式で置いていますので、そちらを使用するかまたはご自身で信号を準備して、是非ノイズの大小やデータ保持率の変化で信号復元がどう機能するかをやってみてください。
そして、背景にある数学的な道具にご興味があれば、下記zennの記事も是非ご覧ください。
魔術の種明かしと、それが技術に変わっていくところを見ることができると思います。