暗号技術勉強メモ

JCA (Java Cryptography Architecture) を学ぶための前提知識として、暗号技術の基本的なところを勉強したときのメモ。

JCA の使い方についてはこちら。

用語

暗号について説明する際に利用される用語について、先に整理しておく。

平文

暗号化されていないメッセージのこと。

暗号化

平文に暗号処理を施して、第三者から内容がわからないようにすること。
暗号化後のメッセージを暗号文と呼ぶ。

復号

暗号文を元の平文に戻す処理のこと。
「復号化」というと怒られる。

アリスとボブ

暗号について説明するときに慣例的に使用される仮の名前。
アルファベットの A, B, C... の順番で名前が考えられており、 Alice, Bob, Carol(もしくは Charlie)... のような感じになっている。

名前ごとに役割が決まっていて、アリスは送信者、ボブは受信者、キャロルは通信の第三者、マロリーは攻撃者、のようになっている。

慣れてくれば、名前から文脈を補完して読めるようになる。

アリスとボブ - Wikipedia

暗号通信に必要な技術

第三者に内容を読まれないように誰かとメッセージをやり取りするにはどうすればいいか？

まずは何より、メッセージ自体を第三者には理解できない形に変換（暗号化）しなければならない。
しかし、メッセージを暗号化しただけでは安全な通信はできない。

暗号化したメッセージを復号するための鍵をどうやってやりとりするのか。
通信相手が確かに意図した相手であることをどうやって保証するのか（第三者のなりすましの可能性）。
もしかしたら、メッセージをまるごと置き換えられるかもしれない。
そもそもの暗号化の方法が弱いと、暗号文を解読されるかもしれない。

もろもろの問題を解決するためには、暗号化だけでなく次のような様々な技術要素が必要になってくる。

• 乱数生成
• ハッシュ関数
• メッセージ認証
• 証明書
• etc...

暗号通信はこれらの技術の組み合わせで実現されている。

それぞれの技術には目的があり、何ができて何ができないのかを理解しておく必要がある。
そうしないと、誤った使い方をして脆弱性を生んでしまうかもしれない。
また、なぜその技術が使われているのかを理解することも難しくなる。

共通鍵暗号

メッセージの送信者と受信者が、暗号化/復号で使用する鍵を共有する方式。
ある鍵で暗号化されたメッセージは、同じ鍵を使用しないと復号できない。
古典的な例では、 シーザー暗号 などが有名。

鍵をあらかじめ安全に共有しておく必要がある（鍵配送問題）。

DES

Data Encryption Standard。
1970年代にアメリカで採用された共通鍵暗号の標準規格。

すでに攻撃方法が見つかっており、現在は新規で採用してはいけない。

AES

Advanced Encryption Standard。
DES の後継として、同じくアメリカで採用された共通鍵暗号の標準規格。

暗号化方式は一般公募され、最終的に Rijndael （ラインダール）というアルゴリズムが採用された。

選考では世界中の暗号学者が候補となったアルゴリズムを検証しており、（今のところ）安全であることが確かめられている。
したがって、下手に暗号方式を自作するよりも、この暗号方式を使ったほうが安全といえる。

公募の条件の１つに「アルゴリズムは無償で無制限に利用できること」があり、このアルゴリズムは誰でも利用できる。
実質、共通鍵暗号のデファクトスタンダードとなっている。

ブロック暗号

AES は平文を一度に暗号化するのではなく、 128 ビットずつに区切って暗号化していく。
このように、メッセージを固定長のまとまり（ブロック）に分けて暗号化していく暗号化アルゴリズムのことをブロック暗号と呼ぶ。
（対して、平文を逐次暗号化していく暗号化アルゴリズムのことをストリーム暗号と呼ぶ）。

メッセージの長さがブロック長の整数倍でない場合（余りが出る場合）は、足りない分を埋めるパディングという処理が施される。

ある平文をブロック暗号で暗号化しようとした場合、単純に考えると先頭から順番にブロック単位に区切って暗号化していけば良い気がする。
しかし、この方法で暗号化すると様々な脆弱性を生むことになる。

平文をブロックで区切ってそのままの順番で暗号化した場合、複数のブロックに同じデータが含まれた場合に、同じ暗号化されたデータが生成されることになる。
つまり、平文のデータが持つパターン（傾向）が、暗号文にも同じように現れるようになる。

また、平文の元々の位置と暗号化後のデータの位置が同じになるので、単純にデータをブロック単位で移動させる（改ざんする）こともできてしまう。
（例えばテキストデータなら、元とは違う意味の文章に変わってしまうかもしれない）

モード

ブロック暗号で暗号化するときは、複数のブロックを単純に暗号化していくと脆弱性を生むことになる。
これを回避するため、ブロック暗号で複数のブロックを暗号化するときの特別な手法（モード）がいくつか考案されている。

ECB

Electoric CodeBook（電子符号表モード）。
これは、最初に挙げた脆弱性のある方法で、平文をブロックにわけて単純に暗号化していくモードになる。

基本的に使用すべきではない。

CBC

Cipher Block Chaining（暗号ブロック連鎖モード）。

CBC では、１つ前の暗号文ブロックを次の平文ブロックの暗号化に利用する（平文と直前の暗号文ブロックの XOR をとってから暗号化する）。

このとき、最初の平文ブロックには「１つ前の暗号文ブロック」が存在しないので、初期化ベクトルというのを用意する必要がある。
初期化ベクトルは、ランダムな値を生成して使用する。

ランダムな値と XOR を取った結果を暗号化するため、暗号文ブロックはランダム性が反映された内容になる。
以後の暗号文ブロックもこのランダム性が連鎖していくため、平文ブロックが同じでも暗号文ブロックはそれぞれ異なる値になる。

この初期化ベクトルは復号のときにも使用する。
したがって、通信相手とは秘密鍵だけでなく初期化ベクトルも共有しておく必要がある。

なお、初期化ベクトルを毎回同じ値にしていると、同じ平文からは毎回同じ暗号文が生成されることになる。
もし攻撃者が２つの通信の暗号文を入手して値が同じであることがわかると、「同じ平文がやりとりされた」という情報を与えてしまうことになる。
したがって、初期化ベクトルは暗号化のたびに生成する方が良い。

その他のモード

他にもいろいろモードが存在するが、詳細は長くなるので省略。
暗号利用モード - Wikipedia などを参照。

• CFB (Cipher FeedBack)
• OFB (Output FeedBack)
• CTR (CounTeR)
• etc...

CRYPTREC | CRYPTREC暗号リスト(電子政府推奨暗号リスト) では CBC, CFB, CTR, OFB が推奨となっている。

公開鍵暗号

共通鍵暗号では、メッセージの暗号化と復号に同じ鍵を使用する。
このため、メッセージをやり取りする送信者と受信者は、鍵を何らかの方法で安全に共有しなければならないという課題がある。

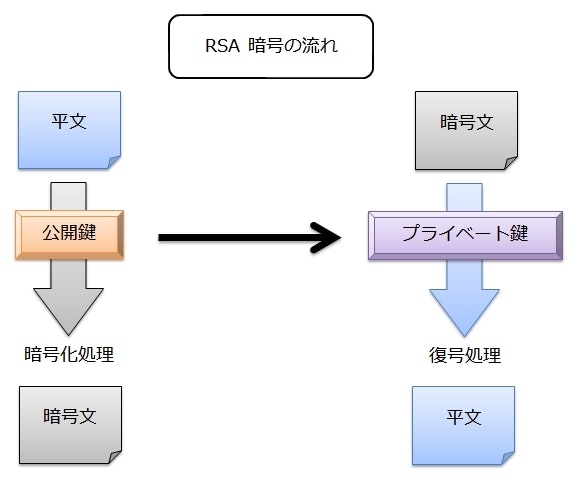
一方、公開鍵暗号では、メッセージの暗号化と復号に異なる鍵を使用する。

暗号化用の鍵を公開鍵（Public Key）と呼び、復号のための鍵をプライベート鍵（Private Key）¹と呼ぶ。
２つはペアで生成し、ちょうど「錠前」（公開鍵）と「解錠のための鍵」（プライベート鍵）のような関係になっている。

ボブ（メッセージの受信者）は、公開鍵を事前にアリス（送信者）に渡しておく。
アリスは公開鍵を使ってメッセージを暗号化し、暗号文を送信する。
そして、ボブは自分が持っているプライベート鍵で暗号文を復号する。

公開鍵からプライベート鍵を推測することが非常に困難になるように設計することで、公開鍵はあらかじめ広く共有しておくことができるようになる。
一方、プライベート鍵は受信者だけが秘匿し、誰にも見られないようにしておく必要がある。

公開鍵暗号は、共通鍵暗号にあった鍵配送問題を解決することができる。
しかし、これですべてが解決したわけではなく、「公開鍵がニセモノにすり替えられていないか」などの問題が引き続き存在している。
これらを解決するにはデジタル署名などの技術が必要になる。

また、公開鍵暗号は共通鍵暗号に比べて処理速度が遅いという問題もある。

RSA

1977年に発明された、公開鍵暗号の最初の具体的な方式。
発明者３人の名前、ロナルド・リン・リベスト（Ronald Linn Rivest）、アディ・シャミア（Adi Shamir）、レオナルド・マックス・エーデルマン（Leonard Max Adleman）から１文字ずつとって RSA 暗号と名付けられた。

２つの巨大な素数を掛け算した値を鍵の一部としている。
解読には巨大な数を素因数分解して、元となった２つの素数を求めなければならない。
しかし、巨大な数の素因数分解は、現在のコンピュータでは現実的な時間で計算できないため安全とされている。

すでに特許切れとなっているため、自由に利用できる。

パディング

この後に RSA の具体的な暗号化方法を書いているが、この方法のまま暗号化をすると脆弱性を生むことになる。

後述の暗号化方法をそのまま適用すると、暗号文は確定的になる。つまり、同じ平文に対して必ず同じ暗号文が生成される。
暗号文が確定的になると、平文のパターンが少ない場合に暗号文から平文を推測できてしまう。

このため、実際の RSA では乱数を含めたパディングを行う。

パディングの仕様は RFC8017 で定義されており、 RSAES-PKCS1-v1_5 と RSAES-OAEP の２つがある。

RSAES-PKCS1-v1_5 は互換性のために残されているもので、新規に利用する場合は RSAES-OAEP を使うのが良さげ。

RSAES-OAEP はアルゴリズムの中でハッシュ関数を利用している。
Java で RSA 暗号を選択した際にパディングを指定するが、パディング名の中には利用するハッシュ関数が含まれている（OAEPWithSHA-1AndMGF1Padding, OAEPWithSHA-256AndMGF1Padding など）。

具体的な暗号化の方法

ここでの説明は、 RSA の雰囲気を掴むことが目的なので、素数は非常に小さい値を選択している。
実際は遥かに大きな値を選択しないと、すぐに暗号は破られるので注意。

前提知識

RSA の暗号化/復号を理解するために必要となる数学の知識をざっくりと。

整数の合同

時計の針は $12$ を $0$ と考えると、 $0$ ～ $11$ までの数字だけを表現できる。
もし $11$ を超えた場合は、また $0$ に戻る（午前・午後の概念は今は除外して考える）。

時計の針で $18$ を表現しようとすると、 $0$ からさらに $6$ 進むことになり、針は $6$ を指す。
つまり、時計盤において $6$ と $18$ は等しいと考えることができる。

$6$ という値は、 $18$ を $12$ で割った余り（剰余）で求めることができる。
このような関係を数学では「法 $12$ において $6$ と $18$ は合同」と表現する²。

数式では $6 \equiv 18 \bmod 12$ と書く。

「法 $n$ において～」と表現した場合は、 $n$ の剰余のことと考えればいい。

互いに素

ある２つの整数 $a$, $b$ があり、その最大公約数が $1$ のとき、 $a$ と $b$ は互いに素と言う。
たとえば、 $12$ と互いに素で $1$ 以上 $12$ 以下の整数は $1$, $5$, $7$, $11$ の４つになる。

オイラーの関数

$\varphi(n)$ で表す関数をオイラーの関数と呼ぶ。

$n$ は正の整数で、この関数は「$n$ と互いに素で $1$ 以上 $n$ 以下の整数の個数」を表す。
例えば $\varphi(12)$ なら、$12$ と互いに素で $1$ 以上 $12$ 以下となる整数は $1$, $5$, $7$, $11$ の４つなので、 $\varphi(12) = 4$ となる。

特に $p$ が素数であれば、 $\varphi(p) = p - 1$ となる。

$p$ は素数なので、 $p$ と $1$ 以外の約数は存在しない。
つまり、 $2$ から $p-1$ までの整数に $p$ の約数は存在しない（存在したら $p$ は素数という前提と矛盾する）。
ということは、 $1$ から $p-1$ の整数は全て $p$ と互いに素ということになるので、$\varphi(p) = p - 1$ となる。

また、オイラーの関数は $p$, $q$ がともに素数の場合、 $\varphi(pq) = \varphi(p)\varphi(q) = (p - 1)(q - 1)$ となる性質がある。

鍵の生成

1. 適当な素数 $p$ と $q$ を決める
2. $p$ と $q$ を掛けた数 $n$ を求める($n = pq$)
3. $\varphi(n)$ より小さくて $\varphi(n)$ と互いに素な正の整数 $e$ を決める
   • 前提知識で説明したオイラーの関数の性質を利用すると $\varphi(n)$ は、
     $\varphi(n) = \varphi(pq) = \varphi(p)\varphi(q) = (p - 1)(q - 1)$ となり、
     $e$ は $(p - 1)(q - 1)$ より小さくて $(p - 1)(q - 1)$ と互いに素である正の整数、と言い換えられる
4. $\varphi(n)$ を法として $e$ の逆数を求め、それを $d$ とする
   • 数式で表すと、 $de \equiv 1 \bmod \varphi(n)$
   • 要するに、 $d$ と $e$ を掛けて $\varphi(n)$ で割った余りが $1$ になるような値 $d$ を求める、ということ

ここで生成した値のうち、 $(n, e)$ のペアが RSA 暗号の公開鍵となる。
そして、 $(n, d)$ のペアがプライベート鍵となる。

鍵	値
公開鍵	$(n, e)$
プライベート鍵	$(n, d)$

暗号化

c = m^{e} \bmod n

$c$ は暗号文、 $m$ は平文を表す。
つまり、 平文 $m$ を $e$ 乗して、 $n$ で割った余りが暗号文 $c$ になる。

復号

m = c^{d} \bmod n

これはつまり、暗号文 $c$ を $d$ 乗して $n$ で割った余りを求めると平文 $m$ が得られる、ということになる。

実際にやってみる

まずは適当な素数 $p$ と $q$ を決める。
とりあえず、 $p = 3$, $q = 13$ とする。

次に $n$ を求める。

\begin{align}
n &= pq \\
  &= 3 \times 13 \\
  &= 39
\end{align}

$e$ を求めるために、 $\varphi(n)$ をまずは計算する。

\begin{align}
\varphi(n) &= (p - 1)(q - 1) \\
 &= (3 - 1)(13 - 1) \\
 &= 2 \times 12 \\
 &= 24
\end{align}

つまり、 $e$ は $24$ より小さい正の整数で、 $24$ と互いに素な数を選ぶ。
とりあえず　 $11$ を選んでみる（$e = 11$）。

最後は $d$ を求める。
$11$ に掛けて $24$ で割った余りが $1$ になるような値なので、とりあえず $d = 35$ としてみる³。
実際に計算すると、

\begin{align}
de \bmod n &= 35 \times 11 \bmod 24 \\
           &= 385 \bmod 24 \equiv 1
\end{align}

ということで、鍵は以下のように決まった。

鍵	値
公開鍵	$(n, e) = (39, 11)$
プライベート鍵	$(n, d) = (39, 35)$

さっそく暗号化をしてみる。
平文 $m = 16$ として、暗号化処理をしてみる。

\begin{align}
c &= m^{e} \bmod n \\
  &= 16^{11} \bmod 39 \\
  &= 17592186044416\bmod 39 \equiv 22
\end{align}

ということで、暗号文 $c = 22$ が得られた。

次は復号処理をしてみる。

\begin{align}
m &= c^{d} \bmod n \\
  &= 22^{35} \bmod 39 \\
  &= 22^{10 + 10 + 10 + 5} \bmod 39 \\
  &= 22^{10} \times 22^{10} \times 22^{10} \times 22^{5} \bmod 39 \\
  &= (22^{10} \bmod 39) \times (22^{10} \bmod 39) \times (22^{10} \bmod 39) \times (22^{5} \bmod 39) \bmod 39 \\
  &= 22 \times 22 \times 22 \times 16 \bmod 39 \\
  &= 170368 \bmod 39 \equiv 16
\end{align}

ちゃんと平文の $16$ が得られた。

ElGamal 暗号

ElGamal の読みは「えるがまる」。

1984 年にエジプトの暗号学者ターヘル・エルガマルが考案した公開鍵暗号の１つ。

整数 $a$ を $x$ 乗して素数 $p$ の剰余を $y$ としたとき（$y = a^{x} \bmod p$）、
$(a, x, p)$ の値から $y$ を求めることは簡単だが、 $p$ が非常に大きな値の場合 $(a, y, p)$ から $x$ を求めること（離散対数問題）は非常に困難という性質を利用している。

具体的な暗号化の方法

前提知識

原始元（生成元）

$p$ が素数で、 $a$ が $p$ と互いに素で $1 \leqq a \leqq p-1$ となる整数のとき、

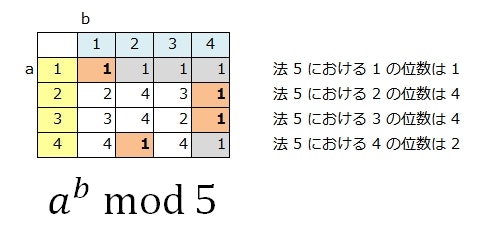
a^{b} \equiv 1 \mod p

となる整数 $b$ （$1 \leqq b \leqq p - 1$）のうち最小のものを、法 $p$ における $a$ の位数と呼ぶ。
要するに、 $b$ 乗して素数 $p$ で割った余りが $1$ になる最小の $b$ のことを指している。

例えば、 $p = 5$ のときは次のようになる。

ここで、位数が $p - 1$ になるような $a$ を、法 $p$ における 原始元 と呼ぶ。
この場合、 $2$ と $3$ が法 $5$ における原始元となる。

原始元（$2, 3$）を累乗して $5$ で割った余りの値を見ると、 $1$ ～ $4$ までの法 $5$ における全ての要素（元）が現れていることがわかる。
つまり、法 $p$ における原始元は、累乗して $p$ の剰余を取ることで、 $1$ ～ $p - 1$ の全ての要素（元）を生成することができる特別な位数ということを意味している。

鍵の生成

1. 素数 $p$ を決める
2. 法 $p$ における原始元 $g$ を選択する
3. $0 \leqq x \leqq p - 2$ となる整数 $x$ をランダムに選択する
4. $g^{x} \bmod p$ で得られる値を $y$ とする

$(p, g, y)$ の３つのセットが公開鍵になる。
そして、 $x$ がプライベート鍵になる。

鍵	値
公開鍵	$(p, g, y)$
プライベート鍵	$x$

暗号化

1. $0 \leqq r \leqq p - 2$ となる整数 $r$ をランダムに選択する
2. $g^{r} \bmod p$ を求め、これを $c_1$ とする
3. $my^{r} \bmod p$ を求め、これを $c_2$ とする
   • $m$ は平文

$(c_1, c_2)$ のセットが暗号文となる。
このため、 ElGamal 暗号では暗号文が平文の２倍程度のサイズになる。

復号

暗号文 $(c_1, c_2)$ から平文 $m$ を求めるには、次のように計算を行う。

m = c_2 c_1^{p - 1 - x} \bmod p

実際にやってみる

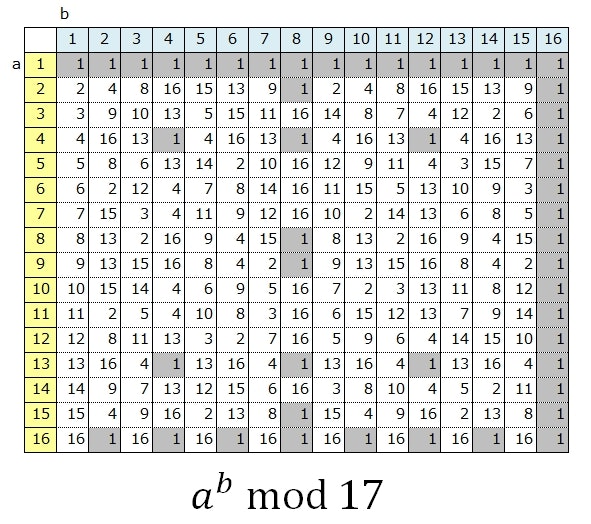
素数 $p$ は、とりあえず $17$ にしてみる。

次に法 $17$ における原始元を調べる。

ここは、とりあえず $5$ を選択してみる。

$x$ は $0$ ～ $15$ の間のランダムな値なので、 $12$ を選択してみる。

最後に $y$ を求める。
ここまでに決めた値から、

\begin{align}
y &= g^{x} \bmod p \\
  &= 5^{12} \bmod 17 \\
  &= 244140625 \bmod 17 \equiv 4
\end{align}

ということで、それぞれの値は次のようになった。

\begin{align}
p &= 17 \\
g &= 5 \\
x &= 12 \\
y &= 4
\end{align}

したがって、公開鍵とプライベート鍵は次のようになる。

鍵	値
公開鍵	$(p, g, y) = (17, 5, 4)$
プライベート鍵	$x = 12$

さっそく公開鍵で暗号化をしてみる。
平文 $m$ は $16$ にする。

$1 \leqq r \leqq p - 2$ となる整数 $r$ をランダムに選択するということなので、とりあえず $9$ を選択してみる。

したがって、暗号文の $c_1$ は次のようになる。

\begin{align}
c_1 &= g^{r} \bmod p \\
    &= 5^{9} \bmod 17 \\
    &= 1953125 \bmod 17 \equiv 12
\end{align}

続いて $c_2$ を求める。

\begin{align}
c_2 &= my^{r} \bmod p \\
    &= 16 \times 4^{9} \bmod 17 \\
    &= 4194304 \bmod 17 \equiv 13
\end{align}

よって、暗号文 $(c_1, c_2)$ は $(12, 13)$ となった。

最後に復号をしてみる。

\begin{align}
m &= c_2 c_1^{p - 1 - x} \bmod p \\
  &= 13 \times 12^{17 - 1 - 12} \bmod 17 \\
  &= 13 \times 12^{4} \bmod 17 \\
  &= 13 \times 20736 \bmod 17 \\
  &= 269568 \bmod 17 \equiv 16
\end{align}

ということで、元の平文を得ることができた。

楕円曲線暗号

1985 年に発明された暗号で、楕円曲線上の離散対数問題の困難性を安全性の根拠としている。

離散対数問題を根拠としている暗号と比べて鍵の長さが短くて済むという特徴がある。
たとえば、鍵長が 2048 ビットの ElGamal 暗号は、鍵長が 256 ビットの楕円曲線暗号と同程度の安全性を持つ。
鍵長が短いということは、それだけ処理時間が短くて済むことになる。

正直、数学的な説明が理解できなかったので詳細は割愛。。。

ハイブリッド暗号

共通鍵暗号は、暗号化の処理は速いが、鍵配送問題がある。
公開鍵暗号は、鍵配送問題はないが、暗号化の処理が遅い。

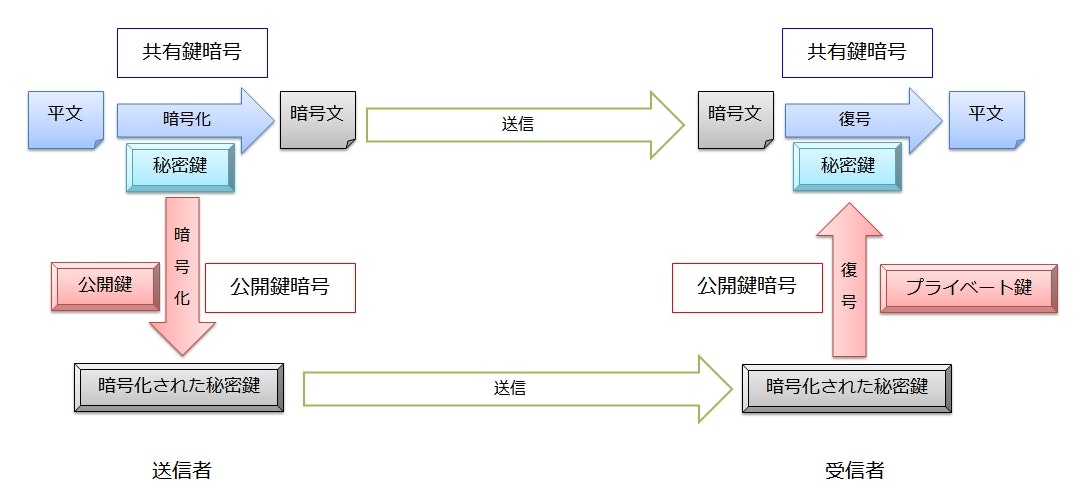
ハイブリッド暗号では、両者のメリットを活かし、デメリットを打ち消すように２つの暗号化方式を組み合わせる。

まず、アリス（送信者）は平文を共通鍵暗号で暗号化する（共通鍵にはランダムに生成した推測困難な値を利用する）。
そして、共通鍵暗号で使用した共通鍵をボブ（受信者）の公開鍵で暗号化し、暗号文とともにボブに送る。
ボブは自分のプライベート鍵で共通鍵を復号し、復号した共通鍵でさらに暗号文を復号する。

平文の暗号化と復号は共通鍵暗号なので処理は高速に行われる。
一方、共通鍵はボブの公開鍵で暗号化されているので、対応するプライベート鍵を持つボブだけが復号できる。

つまり、共通鍵暗号のもつ鍵配送問題を公開鍵暗号で解決しつつ、公開鍵暗号のもつ処理速度の遅さを共通鍵暗号で解決している。

このように、ハイブリッド暗号ではうまい具合に両者のいいとこ取りを実現している。

インターネット通信で利用される SSL/TLS は、このハイブリッド暗号を利用している。

Diffie-Hellman 鍵交換

鍵配送問題を解決する手段の１つとして公開鍵暗号があった。
ところで、この問題を解決する手段はこれだけではなく、 Diffie-Hellman 鍵交換という手法でも解決することができる。

Diffie-Hellman は「でぃふぃー・へるまん」と呼ぶ。

1976 年に考案されたアルゴリズムで、第三者に見られても問題のない値を共有し、双方で共通する秘密鍵を生成することができる。
すでに特許が切れているため、自由に利用することができる。

具体的な手順

1. アリスまたはボブのどちらかが、素数 $p$ と法 $p$ における原始元 $g$ を選択する
2. $p$ と $g$ をアリスとボブの両者で共有する
3. アリスは $1 \leqq a \leqq p - 2$ となる整数 $a$ をランダムに選択する
4. ボブは $1 \leqq b \leqq p - 2$ となる整数 $b$ をランダムに選択する
5. アリスは $g^{a} \bmod p$ を計算しボブに送信する
6. ボブは $g^{b} \bmod p$ を計算しアリスに送信する
7. アリスはボブから受け取った値を $a$ 乗して $p$ の剰余を計算する
   • $(g^{b} \bmod p)^{a} \bmod p = g^{a \times b} \bmod p$
8. ボブはアリスから受け取った値を $b$ 乗して $p$ の剰余を計算する
   • $(g^{a} \bmod p)^{b} \bmod p = g^{a \times b} \bmod p$

これで、アリスとボブは双方で同じ値を得たことになる。

秘密の情報と公開されている情報を整理すると次のようになっている。

• 秘密の情報
  • アリスが選択したランダムな値 $a$
  • ボブが選択したランダム値 $b$
• 公開されている情報
  • 素数 $p$
  • 法 $p$ における原始元 $g$
  • アリスが計算した $g^{a} \bmod p$
  • ボブが計算した $g^{b} \bmod p$

盗聴者が公開されている値から鍵を導出するためには、秘密になっている $a$ または $b$ の情報が必要になる。
しかし、公開されている情報、たとえば $g^{a} \bmod p$ から $a$ を求めるのは離散対数問題になり、非常に困難とされている。

このため、盗聴者は公開されている情報からだけでは鍵を得ることができない。

実際にやってみる

素数 $p$ に $17$ を選択し、原始元 $g$ には $11$ を選んでみる。

アリスが選択した $a$ を $7$ とすると、

\begin{align}
g^{a} \bmod p &= 11^{7} \bmod 17 \\
  &= 19487171 \bmod 17 \equiv 3
\end{align}

となるので、ボブに送信する値は $3$ になる。

一方でボブは $b$ に $15$ を選択したとする。
するとアリスに送信する値は、

\begin{align}
g^{b} \bmod p &= 11^{15} \bmod 17 \\
  &= 4177248169415651 \bmod 17 \equiv 14
\end{align}

となる。

アリスはボブから $14$ という値を受け取るので、生成される鍵は次のようになる。

\begin{align}
(g^{b} \bmod p)^{a} \bmod p &= 14^{7} \bmod 17 \\
  &= 105413504 \bmod 17 \equiv 6
\end{align}

ボブはアリスから $3$ という値を受け取るので、生成される鍵は、

\begin{align}
(g^{a} \bmod p)^{b} \bmod p &= 3^{15} \bmod 17 \\
  &= 14348907 \bmod 17 \equiv 6
\end{align}

ということで、アリスとボブはそれぞれ同じ鍵 $6$ を得ることができた。

ハッシュ関数

ある値を受け取ると、その値を要約した値を返す関数をハッシュ関数と言う。

例えば、次のようなハッシュ関数があったとする。

int hashFunction(int x) {
    return x % 7;
}

このハッシュ関数は、入力値 x に対して 7 で割った余りを返す（% は剰余演算）。
x = 100 なら 14 余り 2 なので 2 を返し、 x = 120 なら 17 余り 1 なので 1 を返す。

ハッシュ関数が返した値は ハッシュ値 と呼ぶ。

ハッシュ関数の性質

決定的である

ハッシュ関数は、入力が同じであれば常に同じハッシュ値を返さなければならない。

つまり、先程のハッシュ関数の例では、 x が 100 であれば常に 2 を返す必要がある。
入力が同じなのに、ある日は 2 を返して別の日は 1 を返していたりしたら、それはハッシュ関数とは呼べない。

ハッシュ値の衝突

前述の例示したハッシュ関数は、 x = 107 の場合も 15 余り 2 なので 2 を返す。
このように、異なる入力を計算して得たハッシュ値が同じになることを衝突と呼ぶ。

例示したハッシュ関数は極端なので簡単に衝突するが、実際のハッシュ関数はもっと衝突が少なくなるように設計されている。

ハッシュ値で入力値を比較する

衝突が起こりづらいハッシュ関数があった場合、そのハッシュ関数で得たハッシュ値は、入力値の識別子として利用できる。
特にハッシュ値が入力値より小さいサイズで生成される場合、ハッシュ値を利用して効率よく入力値を比較できる。

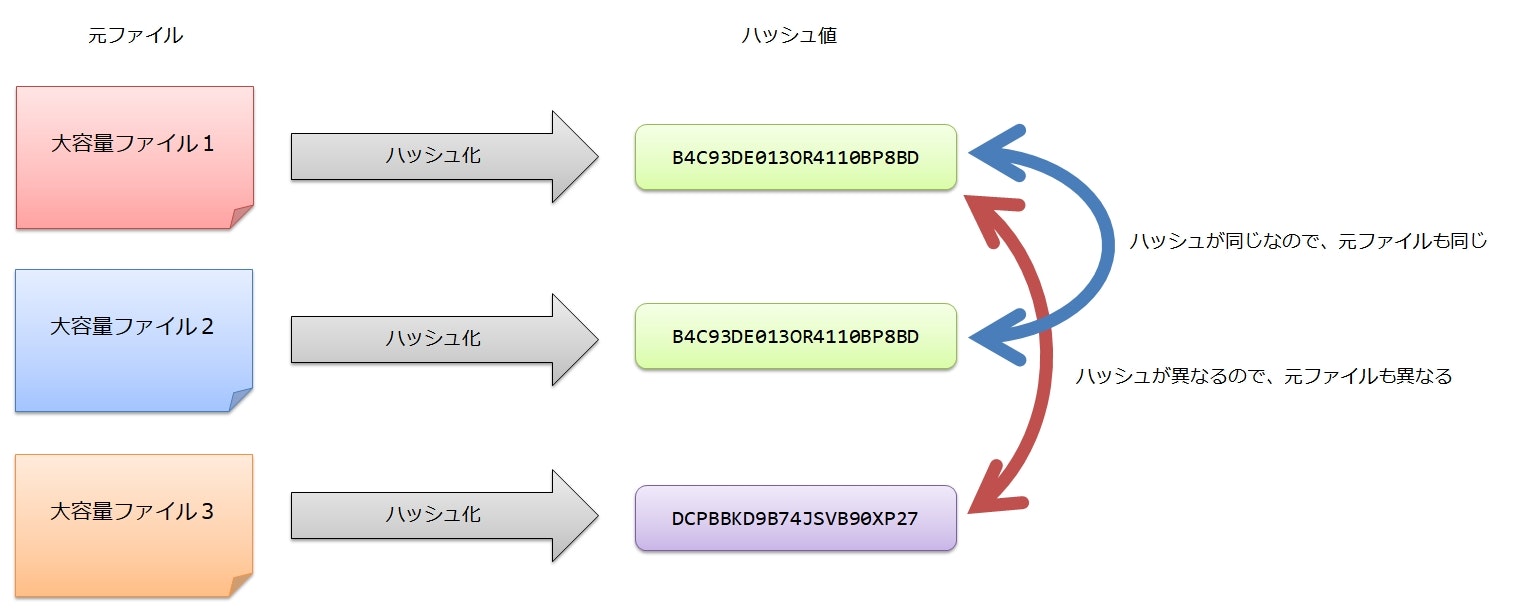
例えば、順番に送られてくる２つの大容量ファイルが同じであることを検証しなければならないとする。
このとき、単純にファイルを比較するのであれば、２つのファイルが届いて比較検証が終わるまでの間、両方のファイルを保持し続けなければならず、データ容量を大きく消費する。

ここでハッシュ関数を使うと、１つ目のファイルはハッシュ値だけを保存（キャッシュ）しておけばよくなる。
２つ目のファイルも同じハッシュ関数でハッシュ値を求め、キャッシュしておいた１つ目のハッシュ値と比較する。
もし２つのファイルが同じであれば同じハッシュ値になるし、ファイルが異なればハッシュ値も異なる値になる。

つまり、ハッシュ値が入力値の識別子として利用できることになる。
（当然、ハッシュ値が衝突しづらいことが前提）

暗号技術におけるハッシュの活用

暗号技術では、このハッシュ関数がよく利用される。

たとえば、パスワードをシステム内に保存するときに、平文ではなくハッシュ値を保存する⁴。
こうすることで、仮にデータベースの内容が漏洩するなどして第三者に見られたとしても、元のパスワードが分からないようにできる。
パスワードの検証は、認証時にユーザが入力したパスワードを再びハッシュ化し、システムが保存しているハッシュ値と比較する。
ハッシュ関数は入力が同じであれば常に同じ結果を返す性質があるため、このようなことができる。

また、デジタル署名でもハッシュ関数が利用されている。
デジタル署名は署名対象のデータが大きいと時間がかかってしまう。
しかし、ハッシュ値であればたいていの場合サイズが大きく減るので、ハッシュ値に対して署名することで計算時間を減らすことができる。
これは、ハッシュ値が元データを要約した識別子としての性質を持つことで可能となっている。

暗号技術で使われるハッシュ関数に求められる性質

ハッシュ関数の具体的なアルゴリズムは多数あり、中には比較的頻繁に衝突が発生するようなものもある。
たとえば、ハッシュテーブルのキーを計算するようなハッシュ関数（Java だと Object#hashCode()）の場合は、衝突自体はわりと発生し得る。

しかし、暗号技術で利用するハッシュ関数では、簡単に衝突が発生すると前述のような用途では利用できない。
暗号技術で利用するハッシュ関数は、ハッシュ関数が持つべき基本的な性質に加えて、次のような特別な性質も持っていなければならない。

弱衝突耐性

ある入力値 x から計算されたハッシュ値 h があったとして、同じハッシュ値 h となる別の入力値 y を見つけることが非常に困難である性質を弱衝突耐性と呼ぶ。

強衝突耐性

同じハッシュ値 h となる異なる２つの入力値 x, y を簡単には見つけられない性質のことを強衝突耐性と呼ぶ。

元データの要約としてハッシュ値を使う以上、ハッシュ値の衝突を任意に引き起こせるような性質は避けられなければならない。
これらの衝突耐性がない場合、元データの識別が正しくできなくなってしまう。

一方向性

元データ→ハッシュ値は当然できるとして、ハッシュ値→元データの逆変換はできないようになっていなければならない。

ハッシュ値から元データが復元できると、例えば先程のパスワード保存での利用はできなくなる。

元データの区別は可能だが元データが何だったのかは分からない、という性質が暗号技術で用いるハッシュ関数には求められる。

具体的なハッシュ関数

実際に暗号技術で使われている（いた）ハッシュ関数は複数存在する。

MD5

Message Digest Algorithm 5 の略。
128 ビットの固定長のハッシュ値を出力する。

すでに攻撃方法（ハッシュ値が同じになる異なる入力値を見つける方法）が確立されているため、現在は使うべきではない。

SHA

Secure Hash Algorithm の略。

2019 年現在、大きく SHA-0, SHA-1, SHA-2, SHA-3 の４つのバージョンが存在する。
いずれも NIST (National Institute of Standards and Technology : アメリカ国立標準技術研究所) によって標準技術として策定された。

SHA は「しゃー」と呼ぶらしく SHA-1 なら「しゃーわん」、SHA-2なら「しゃーつー」と呼ぶらしい⁵。

SHA-0, SHA-1

最初の SHA は 1993 年に発表されたが、間もなく問題点が見つかった。
その後 1995 年に修正版の SHA-1 が発表された。
1993 年の SHA は、他と区別するために SHA-0 と呼ばれたりもする。

SHA-0, SHA-1 は、いずれも 160 ビットの固定長のハッシュ値を出力する。

SHA-2

SHA-1 に改良が加えられた SHA-2 が 2001 年に発表された。
当時はまだ SHA-1 への攻撃が確立されていなかったため、 SHA-1 と SHA-2 はしばらく並行して使われる時期があった。
しかし、 SHA-1 の攻撃方法の研究が進み、 2019 年現在ではすでに使用すべきではないハッシュ関数となっている。

SHA-2 は出力するハッシュ値のサイズの違いによって６つのバリエーションが存在する。

名前	ハッシュ値のサイズ(ビット)
SHA-224	224
SHA-256	256
SHA-512/224	224
SHA-512/256	256
SHA-384	384
SHA-512	512

SHA-224 は SHA-256 で生成したハッシュ値から 32 ビットを切り捨てることで生成している。
また、 SHA-384, SHA-512/224, SHA-512/256 は、 SHA-512 で生成したハッシュ値からそれぞれ 128 ビット, 288 ビット, 256 ビットを切り捨てることで生成している。

SHA-2 への攻撃方法は、 2019 年 4 月現在はまだ確立されていない。

SHA-3

SHA-1 の攻撃方法が徐々に見つかりだしたことで、新しいハッシュ関数の公募が NIST によって行われた。
最終的に、 2012 年に Keccak （ケチャック）というアルゴリズムが選ばれた。

SHA-3 にも、 SHA-2 と同様にハッシュ値のサイズによって６つのバリエーションが存在する。

名前	ハッシュ値のサイズ(ビット)
SHA3-224	224
SHA3-256	256
SHA3-384	384
SHA3-512	512
SHAKE128	任意長
SHAKE256	任意長

2019 年 4 月現在、こちらも攻撃方法は確立されていない。
しかし、 SHA-2 も現役（まだ破られていない）なので、必ずしも SHA-3 を選択しなければならないというわけではない。

メッセージ認証コード

通信相手からメッセージを受け取ったとする。

そのメッセージが、

1. 改ざんされていないこと
2. 確かに通信相手が送ったメッセージであること

ということは、そのメッセージだけでは判断できない

これらを検証するための技術として、 メッセージ認証コード というものが存在する。
メッセージ認証コードは、 Message Authentication Code の頭文字を取って MAC と呼ばれる。

メッセージ認証コードの手順

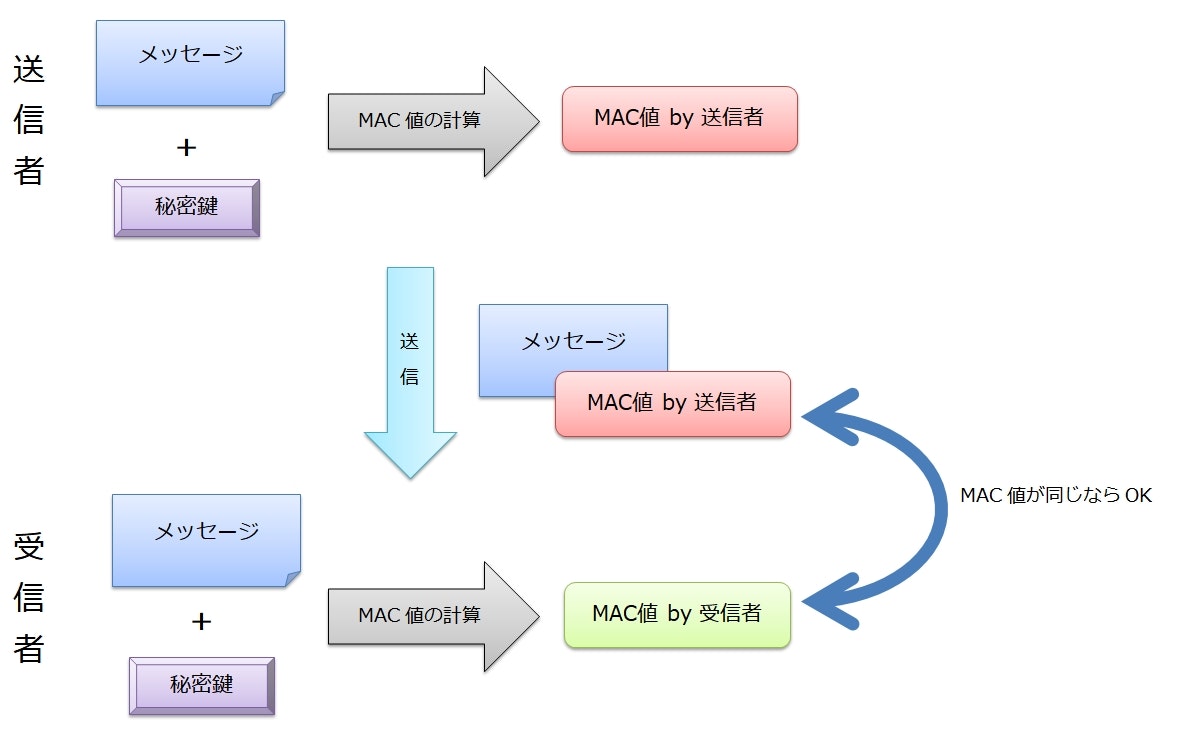
メッセージ認証コードでは、まず通信者同士で秘密の鍵を決めて共有しておく。
次に、送信するメッセージと秘密鍵を合わせたものを変換し、別の固定長の値――MAC値を生成する。
（この変換には、たとえばハッシュ関数などを利用する）

アリス（送信者）は、メッセージと MAC 値の２つを送信する。

ボブ（受信者）は、受け取ったメッセージと、自分が持つ秘密鍵を使って、アリスと同じように MAC 値を計算する。
そして、ボブは自分が計算した MAC 値とアリスが送ってきた MAC 値が一致することを検証する。

MAC 値は「改ざんされていない正しいメッセージ」と「通信者同士で共有している秘密の鍵」の２つが揃って初めて正しい値を計算できる。
したがって、 MAC 値が一致していれば、「メッセージが改ざんされていないこと」と「送信者がアリスのなりすましではないこと」の２つが確認できたことになる。

MAC は、あくまで改ざん検知が目的なので、メッセージの機密性は保護されていない。
機密性の確保は、暗号化で別途対応しなければならない。

また、秘密鍵は事前に共有しておく必要があるので、共通鍵暗号と同じく鍵配送問題が発生する。

実装方法

HMAC

MAC 値の計算にハッシュ関数を利用する手法として、 HMAC (H は Hash の H) が存在する(RFC2104)。
HMAC では、 SHA-1 や SHA-2 のハッシュ関数などを利用する（HMAC-SHA1, HMAC-SHA-256, HMAC-SHA-512 など）。
ハッシュ関数は限定されていないので、もしハッシュ関数の攻撃方法が発見されたら、より強固なハッシュ関数に切り替えることができる。

AES-CMAC

AES （共通鍵暗号）の CBC モードで暗号化を行い、最後のブロックの暗号結果だけを MAC 値として利用する方法があり、 AES-CMAC(RFC4493)と呼ぶ。

CBC モードで暗号化した最終ブロックは、それまでのブロックの暗号結果からできる値なので、 MAC 値として利用できる（正しいメッセージとただしい共通鍵がなければ、最終ブロックは計算できない）。

メッセージ認証コードの限界

第三者に共有できない

メッセージ認証コードで通信相手がなりすましでないことを確認できているのは、「秘密鍵を知っているのはアリス（送信者）とボブ（受信者）だけ」ということが前提となっている。

もしボブがアリスから受け取った MAC 値とメッセージをキャロル（第三者）に共有しても、キャロルはその MAC 値がアリスによって作られたことを確信できない。
キャロルが MAC 値の正当性を検証するためには秘密鍵を共有する必要がある。もし秘密鍵をキャロルに開示しても、秘密鍵はアリスだけでなくボブも知っている。このため、ボブがアリスと偽って MAC 値を生成した可能性をキャロルは否定できない。

つまり、メッセージ認証コードでなりすましを検出できるのは、秘密鍵を共有している二者間でのみということになる。

否認を防止できない

否認とは、アリス（送信者）が「いや、そんなメッセージ送信してないし」とメッセージの送信を認めないことを言う。

「秘密鍵」さえ知っていれば、任意のメッセージから MAC 値を生成することができる。
つまり、「秘密鍵」を持っているボブ（受信者）も、その気になれば好きなメッセージから MAC 値を生成できる。

もしアリスに「そんなメッセージと MAC 値を送った覚えはない。ボブが自分で勝手に作ったものじゃないの？」と言われると、ボブはそれを否定することができない（原理上、確かにボブは好きなメッセージと MAC 値の組み合わせを作ることができてしまうので）。

再生攻撃

メッセージ認証コードを利用した通信データ（メッセージと MAC 値）をマロリー（攻撃者）が盗み、何度も繰り返し送信（再送）したとする。

ボブ（受信者）は同じ通信データを何度も受け取ることになる。
しかし、受け取ったメッセージと MAC 値の組み合わせは確かに正しいものなので、ボブからはそれが「本当に繰り返し送信されたもの」なのか「マロリーが偽って送信してきたもの」なのかを区別できない。

通信データの内容によっては、繰り返し受け取ると危険な場合もある（システムのデータを更新するようなデータなど）。

このような攻撃を再生攻撃と呼ぶ。

再生攻撃を防ぐには、 MAC 値を計算するときにメッセージごとに異なる値（シーケンス番号やランダムな値（ノンスと呼ばれる）など）を加えることで、再送を検知するような方法がある。

共通鍵暗号だけでは不足？

受信したデータを共通鍵暗号で復号し正しい平文が得られれば、「メッセージが改ざんされていないこと」と「送信者がなりすましでないこと」を検証できそうな気がする。

しかし、これには「復号の結果、正しい平文を得られたかどうか」を判断することができない、という問題がある。
平文が分かりやすい構造の文書などであれば、「正しい平文になったっぽい」ことはわかるかもしれない。
しかし、そもそもの平文がランダムな文字列などであれば、「正しい平文」を得られたかどうかは判断できない。

メッセージ認証コードには、元のメッセージの形式にかかわらず改ざんされていないことを判定できるという特徴がある。

デジタル署名

メッセージ認証コードでは、第三者に共有できなかったり、否認を防止できないという課題があった。

デジタル署名の技術を使うと、これを解決できる。

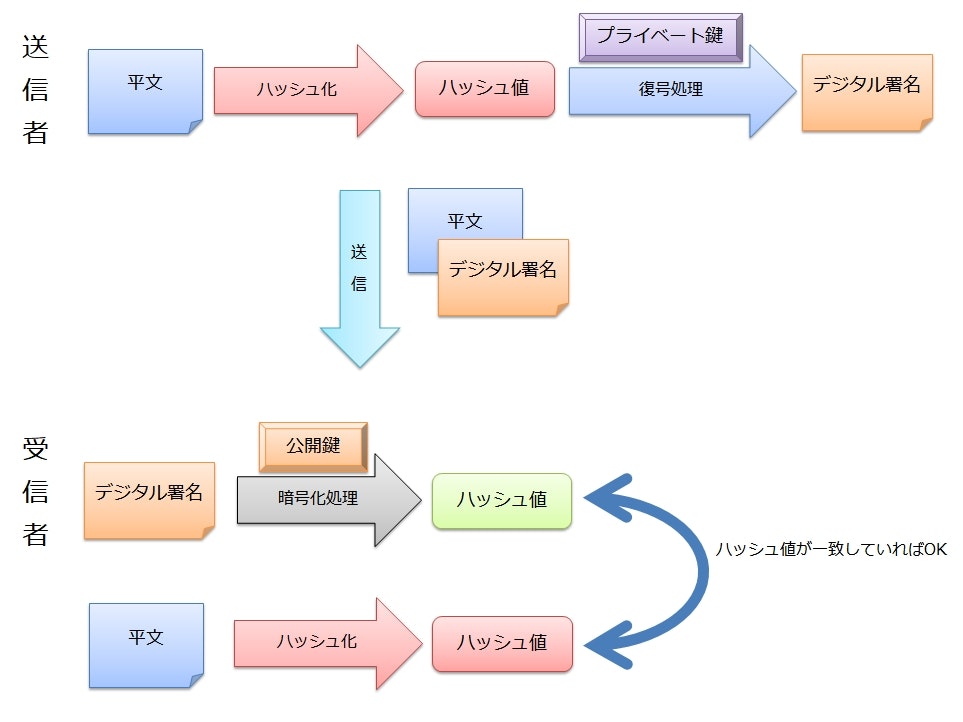
デジタル署名の基本的な仕組み

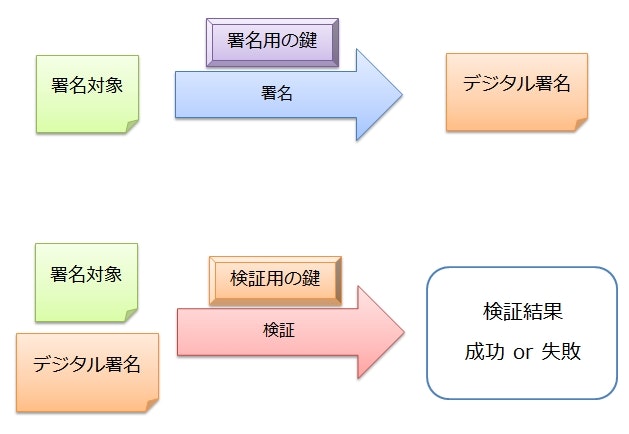
デジタル署名では、署名と検証という２つのステップが存在し、それぞれで異なる鍵を使用する。

アリス（デジタル署名をする人）は署名用の鍵と検証用の鍵を事前に生成しておく。
そして、生成した鍵のうち署名用の鍵はアリスが保管して秘密にし、検証用の鍵は広く公開する。
ボブ（デジタル署名を受け取り検証する人）は、公開された検証用の鍵を事前に入手しておく。

アリスは署名用の鍵を使用し、メッセージ（署名対象）からデジタル署名を生成する。
「署名」と聞くと現実世界でのサインのようなものをイメージし、固定の値のようなものと想像してしまうかもしれない。
しかし、実際のデジタル署名は固定値ではなく、署名対象ごとに固有の値となる（固定値だと、デジタルデータでは簡単にコピーできてしまう）。

アリスは、メッセージとデジタル署名の両方をボブに送信する。
ボブは、受け取ったメッセージとデジタル署名の関係が正当であることを、検証用の鍵を用いて確認する。

デジタル署名で使用する署名用の鍵と検証用の鍵は、密接なペアとなっている。
検証用の鍵で検証した結果が成功したということは、そのデジタル署名はペアとなっている署名用の鍵で作られたことになる。
そして、その署名用の鍵はアリス本人のみが持っている前提なので、デジタル署名は確かにアリス本人によって作成されたことが確認できたことになる（否認防止になる）。

また、デジタル署名は第三者のキャロルに渡しても、そのデジタル署名がアリスによって作成されたことを検証できる。

RSA を用いたデジタル署名

具体的なデジタル署名の方法として、公開鍵暗号の RSA を使用する方法がある。

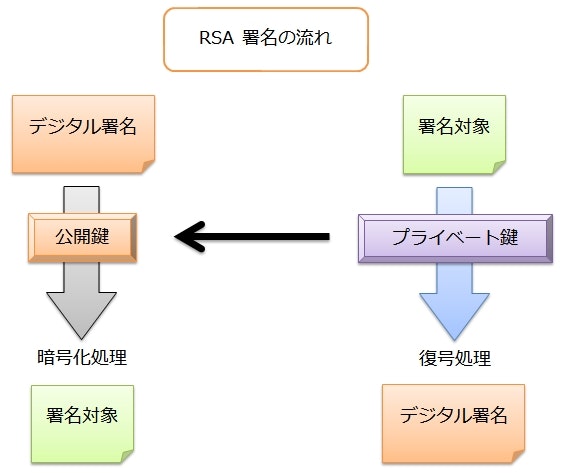
RSA 暗号では、公開鍵を用いて暗号化を行い、プライベート鍵を用いて復号を行った。

RSA をデジタル署名として用いる場合は、これを逆転させる。

公開鍵暗号として利用するときは、プライベート鍵の復号には暗号文を渡したが、ここに署名対象のメッセージを渡す。
変換結果がデジタル署名となり、これを元のメッセージとともに送信する。

受信者は、公開鍵の暗号化処理の入力にデジタル署名を渡す。
すると、デジタル署名をもとのメッセージに戻すことができる。

デジタル署名とともに受信した元のメッセージとデジタル署名を変換して得た結果に差がなければ、デジタル署名の検証は成功したことになる。

ハッシュ化してからデジタル署名を作る

デジタル署名の対象に平文を利用することは当然可能だが、平文のサイズが大きいと処理に時間がかかる。

そこで、実際の署名では平文のハッシュ値に対してデジタル署名を行う。
大抵の場合、ハッシュ値は平文よりも短くなるので、処理時間を短縮することができる。

受信者は、デジタル署名を変換して得られたハッシュ値と、平文を自らハッシュ化して得た値を比較することで検証を行う。

実際にやってみる

RSA 暗号で試したときの公開鍵とプライベート鍵を再利用する。

鍵	値
公開鍵	$(n, e) = (39, 11)$
プライベート鍵	$(n, d) = (39, 35)$

署名対象のメッセージを $m = 15$ とすると、デジタル署名 $s$ は次のようになる。

\begin{align}
s &= m^{d} \bmod n \\
  &= 15^{35} \bmod 39 \\
  &= 15^{10 + 10 + 10 +5} \bmod 39 \\
  &= 15^{10} \times 15^{10} \times 15^{10} \times 15^{5} \bmod 39 \\
  &= (15^{10} \bmod 39) \times (15^{10} \bmod 39) \times (15^{10} \bmod 39) \times (15^{5} \bmod 39) \bmod 39 \\
  &= 36 \times 36 \times 36 \times 6 \bmod 39 \\
  &= 279936 \bmod 39 \equiv 33
\end{align}

デジタル署名は $s = 33$ となった。

今度は、公開鍵を使ってこの署名を検証する。

\begin{align}
m &= s^{e} \bmod n \\
  &= 33^{11} \bmod 39 \\
  &= 50542106513726817 \bmod 39 \equiv 15
\end{align}

無事、もとのメッセージが得られた。

デジタル署名の悪用

RSA によるデジタル署名は、メッセージ（署名対象）をプライベート鍵による復号処理に渡すことで生成している。

このことをうまく悪用すると、公開鍵で暗号化された暗号文をプライベート鍵の所有者自身に復号させる攻撃が実現できる。
つまり、例えば「このメッセージにデジタル署名をつけてください」と言って公開鍵で暗号化された暗号文を渡す。
依頼された側が、メッセージの内容を確認せずに暗号文にデジタル署名をすると、暗号文は復号され、平文になってしまうことになる。

この攻撃に対する対策としては、

• メッセージを直接署名するのではなく、ハッシュ値に署名する
• 公開鍵暗号用の鍵ペアと、署名用の鍵ペアを分けて運用する
• よくわからないものに安易に署名しない

などがある。

デジタル署名≠公開鍵暗号の逆処理

デジタル署名の説明で、よく「公開鍵暗号を逆転させたもの」という説明がされることがある。
しかし、これが成り立つのは RSA 暗号の場合のみで、他の公開鍵暗号では逆転させてもデジタル署名を実現できるとは限らない。

例えば、同じ公開鍵暗号の ElGamal 暗号は逆転してもデジタル署名には利用できない。
ElGamal 暗号は、暗号化と復号で入出力の数が違っているため逆転させることができない（暗号化時は入力が $m$ で出力が $(c_1, c_2)$ 、復号時は入力が $(c_1, c_2)$ で出力が $m$）。

ちなみに ElGamal 署名というものも存在するが、これは ElGamal 暗号と同じ人が考えたというだけで、内容は ElGamal 暗号を逆転させたものではない。

ElGamal 署名

ElGamal 暗号の考案者であるターヘル・エルガマルが考案したデジタル署名。
こちらも「離散対数問題」が困難という性質を利用している。

ただし、現在は基本的に利用されることはなく、改良版の DSA が利用されている。

デジタル署名の手順

前提知識

法n における a の逆数

法 $n$ における $a$ の逆数（$a^{-1}$）は、「$a$ に掛けて $n$ の剰余を取ると $1$ になる数」と考える。

数式で表すと、 $ab \equiv 1 \bmod n$ となる $b$ が $a$ の逆数となる。

たとえば、 $n = 7$ で $a = 3$ であれば、 $b = 5$ となる。

\begin{align}
ab \bmod n &= 3 \times 5 \bmod 7 \\
  &= 15 \bmod 7 \equiv 1
\end{align}

つまり、法 $7$ における $3^{-1}$ は $5$ ということになる。

鍵の生成

ElGamal 署名の鍵生成は、 ElGamal 暗号と同じになっている。

鍵	値
公開鍵	$(p, g, y)$
プライベート鍵	$x$

署名

1. $p - 1$ と互いに素で $1 \leqq t \leqq p - 1$ となる整数 $t$ をランダムに選択する
2. $g^{t} \bmod p$ を計算し、これを $r$ とする
3. $t^{-1}(m - xr) \bmod p - 1$ を計算し、これを $s$ とする
   • $m$ は署名対象のメッセージ

ここで得られた $(r, s)$ のペアが、メッセージ $m$ に対するデジタル署名となる。

検証

1. $1 \leqq r \leqq p - 1$ が成り立つか検証する
   • 成り立つ場合は次の手順に進む
   • 成り立たない場合は検証失敗で終了
2. $g^{m} \equiv y^{r} r^{s} \bmod p$ が成り立つか検証する
   • 成り立つ場合は検証成功で終了
   • 成り立たない場合は検証失敗で終了

実際にやってみる

ElGamal 暗号のときに使用した鍵を再利用する。

鍵	値
公開鍵	$(p, g, y) = (17, 5, 4)$
プライベート鍵	$x = 12$

まずは $p - 1 = 16$ と互いに素で $1 \leqq t \leqq 16$ となる整数 $t$ をランダムに選択する。
とりあえず $13$ にしてみる。

次に $r$ を計算する。

\begin{align}
r &= g^{t} \bmod p \\
  &= 5^{13} \bmod 17 \\
  &= 1220703125 \bmod 17 \equiv 3
\end{align}

署名対象のメッセージを $m = 9$ とした場合、 $s$ は次のようになる。

\begin{align}
s &= t^{-1}(m - xr) \bmod p - 1 \\
  &= 13^{-1}(9 - 12 \times 3) \bmod 16 \\
  &= 5 \times -27 \bmod 16 \\
  &= -135 \bmod 16 \equiv -7
\end{align}

デジタル署名は $(r, s) = (3, -7)$ となった。

次は検証を試みる。

$1 \leqq r \leqq p - 1$ は当然満たしているので、ここはパス。
$g^{m} \equiv y^{r} r^{s} \bmod p$ が成り立つかを確認する。

\begin{align}
g^{m} \bmod p &= 5^{9} \bmod 17 \\
  &= 1953125 \bmod 17 \equiv 12
\end{align}

\begin{align}
y^{r} r^{s} \bmod p &= 4^{3} \times 3^{-7} \bmod 17 \\
  &= 64 \times (3^{-1})^{7} \bmod 17 \\
  &= 64 \times 6^{7} \bmod 17 \\
  &= 64 \times 279936 \bmod 17 \\
  &= 17915904 \bmod 17 \equiv 12
\end{align}

ということで、どちらも法 $17$ において $12$ となったので、検証は成功ということになる。

DSA

Digital Signature Algorithm の略。
NIST が 1991 年に定めたデジタル署名の規格（DSS）用のアルゴリズム

ElGamal 署名を改良して作られた。
具体的なアルゴリズムなどは割愛。

デジタル署名の限界

デジタル署名の効力は、「検証用の鍵が本物であること」が大前提となっている。
もし検証用の鍵自体が攻撃者によって差し替えられていると、デジタル署名は意味をなさなくなる。

つまり、デジタル署名を利用するためには、まず最初に信頼できる方法で検証用の鍵を入手しなければならない、ということになる。

一番確実なのは、デジタル署名をする本人から直接検証用の鍵をもらうことだが、インターネットを介して様々な相手と通信するとなると現実的ではない。

これを解決できないと、デジタル署名は意味をなさないことになる。

認証局と証明書

デジタル署名を利用すれば、メッセージの改ざんを検知でき、署名した相手の認証、否認防止などができる。
しかし、デジタル署名の効力を得るためには、検証用の鍵が本物であることが前提となる。

また、公開鍵暗号を使う場合も、そもそも暗号化に利用しようとしている公開鍵が本物であることが前提となっている。

ある公開鍵（以後、デジタル署名の検証鍵も含む）が本物であることを証明するための仕組みとして、認証局（Certificate Authority, CA） と 証明書 （certificate）というものが存在する。

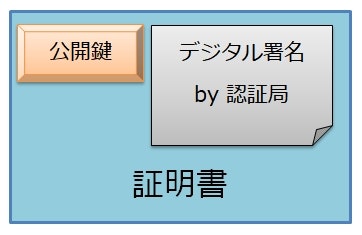
証明書は、「この公開鍵は確かに本物です」ということを証明するもので、認証局によって作成される。
証明書の実体は、公開鍵自体と認証局が公開鍵に対して作成したデジタル署名のセットとなっている。

アリス（公開鍵の証明書を作成してもらいたい人）は、作成した公開鍵を認証局に提出し証明書の発行を依頼する。
このとき、認証局はアリスの本人確認を行い、その公開鍵が確かにアリスのものであることを確認する。

本人確認ができると、認証局は公開鍵が本物であることを保証するためにデジタル署名を作成し、証明書として発行する。
つまり、証明書があるということは、その公開鍵は認証局によって本人確認がされている、ということになる。

認証局は誰が運営しているか

認証局を運営するための免許などは特に必要なく、個人で認証局を名乗って証明書を発行することもできる。

しかし、その役割から想像できるように、認証局は責任が重大で利用者から信頼されていることが重要になる。
個人で認証局を運営して証明書を発行しても、利用者が認証局を信頼せず、証明書を利用しなければ意味がない。

インターネット上で利用されるような証明書は、企業が事業として運営している認証局や、政府が運営している認証局などから発行されている。
（Let's Encrypt のような非営利団体による認証局もある）

企業や学校内などの閉じられたネットワーク内だけで利用するのであれば、プライベートな認証局を運営する方法もある。

証明書の検証

証明書は、認証局が本人確認をしたうえで作成されている。
しかし、入手した証明書が本物かどうかを確認できないと結局意味がない。

証明書には認証局のデジタル署名が含まれている。
したがって、そのデジタル署名を検証することで証明書の真偽は確認できる。
しかし、そのためには認証局の公開鍵が必要になる。

すると次は、認証局の公開鍵はどうやって入手するのか？　という問題が発生する。

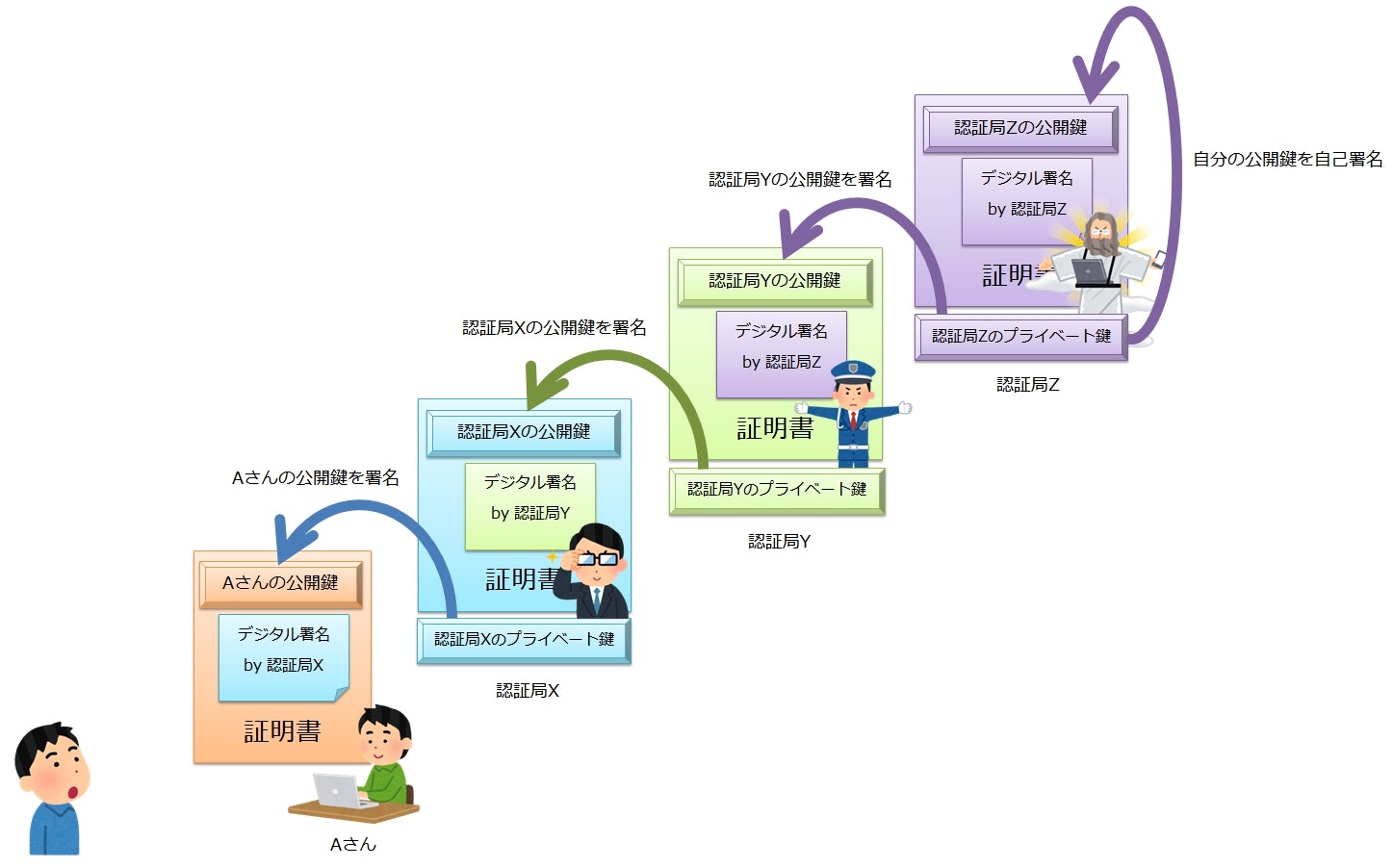
証明書の連鎖

認証局の公開鍵の正当性は、別のより信頼の強い認証局によって保証されている。
つまり、認証局の公開鍵は、別の認証局から証明書が発行されている。

では、その別の認証局の公開鍵は誰が保証しているのか？
それもまた、更に上位の認証局によって証明書が発行されている。

このように、証明書は、より上位の認証局によって証明書が発行され、鎖のようにつながった構造になっている。

証明書の連鎖には終りがあり、最終的にたどり着いたトップの証明書のことを ルート証明書 と呼ぶ。そして、ルート証明書を発行している認証局を ルート認証局 と呼ぶ。

ルート証明書にもデジタル署名が施されているが、その署名者はルート認証局自身になっている。
つまり、自分のプライベート鍵で自分の公開鍵を署名していることになる。このような証明書のことを、自己署名証明書と呼ぶ（俗に言う「オレオレ証明書」）。

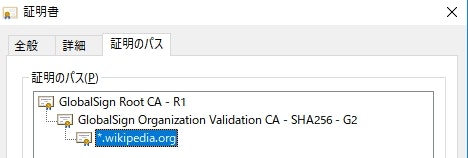
試しに Wikipedia の証明書を確認してみる。
アドレスバーの錠前のマークをクリックすると、現在接続しているサーバーの証明書を確認することができる（※ブラウザ：Chrome、OS：Windows 10）。

証明書が二段階に連鎖しているのがわかる。

認証局自体は無数に存在するため、それら１つ１つについて「信頼できるか？」を判定するのは大変すぎる。
しかし、証明書がこのように連鎖し、最終的にいくつかのルート認証局にたどり着くようになっていれば、そのいくつかのルート認証局に対してのみ「信頼できるか？」を判定すればよくなる。

Web ブラウザなどの暗号通信を行うソフトウェアには、そのソフトウェアを開発したベンダが「信頼できる」としたルート証明書があらかじめ組み込まれている。
ソフトウェアを使うユーザは、「このベンダが選んだルート認証局なら、まぁ安心できるか」という信頼のもと、そのソフトウェアを使って暗号通信を行うことになる。

証明書を無効にする

アリス（証明書を発行してもらった人）が誤ってプライベート鍵を漏洩させるなどして、特定の証明書を無効にしなければならなくなることがある。

この場合、アリスは速やかに認証局に証明書を無効にする依頼を出す必要がある。
依頼を受けた認証局は、証明書破棄リスト (certificate revocation list：CRL)にアリスの証明書を追加して公開する。

CRL には無効になった証明書のシリアル番号（証明書を識別するキー情報）が載っている。
証明書を利用しているアプリケーションなどは、認証局が発行する CRL を常に最新化して、無効になった証明書は信頼しないように制御しなければならない。

CRL の入手方法

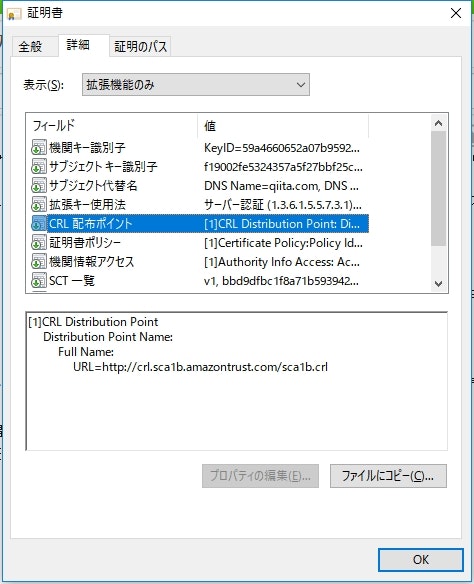
CRL を入手できる URL は、証明書に記載されている。
（ここ以外に入手先の確認方法があるのかどうかは、よく分かってない）

Qiita の証明書をブラウザで見てみると、「CRL 配布ポイント」というフォールドに http://crl.sca1b.amazontrust.com/sca1b.crl と記載されている。

ここにアクセスすると、 CRL を入手できる（バイナリファイル）。

OCSP

CRL を使った確認の場合、定期的に CRL が最新化されていないか確認しなければならない。
もし CRL の更新を忘れて古い情報で検証をしていると、実は無効化されていて信頼すべきでない証明書も信頼してしまうかもしれない。

これに対して、リクエストの際にオンラインで対象の証明書が無効になっていないか確認するプロトコルが存在する。
これを OCSP (Online Certificate Status Protocol) と呼び RFC6960 で標準化されている。

認証局が信頼できなくなるとどうなるか

もし認証局が何らかの理由で信頼できなくなった場合⁶、その認証局が発行する証明書は基本的に全て信頼できなくなる。

ブラウザベンダーなどは、その認証局を信頼できる認証局から除外するアップデートを入れることで、以後その認証局が発行した証明書で警告を出すようになるかもしれない。

実際、最近シマンテックの認証局が信頼できなくなったとして、 Google Chrome や Firefox などのブラウザがシマンテックの認証局が発行した証明書を無効にするアップデートを入れている。

「Firefox 63」でSymantec発行のTLS証明書が無効に ～トップ100万サイトの3.5％に影響 - 窓の杜

内部で証明書を保持している Java も、 12 のリリースでシマンテックの証明書を削除している。

[JDK-8207258] Distrust TLS server certificates anchored by Symantec Root CAs - Java Bug System

証明書の標準規格

証明書には X.509 という標準規格が存在する（RFC5280）。

この規格では証明書に載せる情報などが決められていて、次のような情報が載っている。

• 証明書のシリアル番号
• 証明書の発行者
• 公開鍵の所有者
• 有効期限（開始日時/終了日時）
• ハッシュ化で使用したアルゴリズム
• 鍵の種類
• etc...

世の暗号通信を行うアプリケーションは、だいたいこの規格をサポートしている。

ファイルフォーマット

X.509 証明書のデータ構造は、ASN.1 というバイナリデータ構造を表現する記法で定義されている。
そして、 DER （Distinguished Encoding Rules）というエンコーディング方法でバイナリ化されたものが証明書ファイルとして用いられる。

さらに、この DER ファイルを Base64 でエンコーディングしてテキストにしたファイル（PEM ファイル）もよく利用される。
PEM ファイルは、 -----BEGIN ～～ の行で始まり -----END ～～ の行で終わる形になっている。

openssl や keytool などのツールは、 DER や PEM での証明書の入出力をサポートしている。

詳しくは RSA鍵、証明書のファイルフォーマットについて - Qiita が分かりやすいです。

証明書署名要求

自分が所有している公開鍵の証明書を認証局に発行して貰う場合、公開鍵や証明書に載せる識別名などの情報を認証局に渡す必要がある。

この認証局に渡す情報をまとめたファイルは RFC2986 で標準化されており、証明書署名要求（CSR, Certificate Signing Request）と言う。

認証局に証明書の発行依頼をするときは、この証明書署名要求を作成して渡すことになる。

公開鍵基盤（PKI）

公開鍵暗号の仕組みだけでは安全な暗号通信は実現できない。
公開鍵を安全にやり取りするための仕組みが必要になり、そのためにはデジタル署名・証明書・認証局などに加え、他にも様々なルールや仕組みが必要になる。

これら公開鍵を運用するために必要となる様々な要素をまとめて公開鍵基盤（public-key infrastructure：PKI）と呼ぶ。
認証局や X.509 も、この PKI の一部といえる。

鍵

ここまで、様々なところで様々な「鍵」が登場した。

• 共通鍵暗号の秘密鍵
• 公開鍵暗号の公開鍵・プライベート鍵
• メッセージ認証コードの秘密鍵
• デジタル署名の署名鍵・検証鍵

鍵は、暗号化技術の要（かなめ）となる。
どんなに暗号化技術が高度で解読困難であっても、鍵さえ知ってしまえば誰でも復号ができてしまう。

したがって、鍵は安易に推測できるような値にしてはいけない。
また、鍵の総数が少ないと総当たり攻撃で解読されるかもしれないので、鍵のサイズ（鍵長）も重要になる。

たとえば共通鍵暗号の AES では、鍵のサイズは 128, 192, 256 ビットのいずれかを選択する。
仮に 256 ビットの鍵を選択した場合、その総数は $115792089237316195423570985008687907853269984665640564039457584007913129639936$ 通りになる。

参考：覚え書き: 2 の 256 乗を計算してみた

総当たりしても地球が先に滅ぶかもしれない。

推奨される鍵長

鍵長を長くすればそれだけ安全性は高まるが、同時に処理時間も長くなる。
NIST が公開している Recommendation for Key Management, Part 1: General という資料に、最低どれくらいの長さの鍵を利用すべきかの指針が説明されている。

等価安全性

異なる暗号化アルゴリズムの安全性を同じ尺度で比較する方法として等価安全性というものがある。

等価安全性では、その暗号化アルゴリズムを最善の手法で解読した場合に必要となる計算量（解読計算量）で安全性を比較する。
解読計算量が $2^{k}$ の場合、その暗号化アルゴリズムは「$k$ ビット安全性を持つ」と表現する。
$k$ の値が大きいほど、安全性は高いことになる。

暗号化アルゴリズムごとの安全性

ある暗号化アルゴリズムにおける安全性は、その暗号化アルゴリズムで使用する鍵の長さで決まる。
例えば、共通鍵暗号で $128$ ビット安全性を持たせるためには、鍵長を $128$ ビットにすればいい。

公開鍵暗号の場合は、「素因数分解問題ベース（IFC: Integer Factorization Cryptosystems）」か「離散対数問題ベース（FFC: Finite Field Cryptosystems）」か「楕円曲線上の離散対数問題ベース（ECC: Elliptic Curve Cryptosystems）」かによって鍵長になる対象が変わってくる。

IFC の場合、鍵生成で使用する２つの素数 $p, q$ を掛けた数 $N$ のビット長が鍵長となる。
FFC の場合、 $y \equiv g^{x} \bmod p$ の $x, y$ それぞれのビット長が鍵長となる。
ECC の場合、 $Y = xG$ の $Y$ のビット長が鍵長となる。

また、ハッシュ関数の場合はハッシュサイズが鍵長となる。

暗号化アルゴリズム	鍵長	112ビット安全性	128ビット安全性	192ビット安全性	256ビット安全性
共通鍵暗号	共通鍵のビット長	112	128	192	256
IFC	N のビット長	2048	3072	7680	15360
FFC	(y のビット長, x のビット長)	(2048, 224)	(3072, 256)	(7680, 384)	(15360, 384)
ECC	Y のビット長	224～255	256～383	384～511	512～
ハッシュ関数	ハッシュサイズ	224	256	384	512

現在および将来推奨される安全性

コンピュータの性能や解読技術は年々向上しているため、現在安全な鍵長でも将来的には安全でなくなる可能性がある。

先述の NIST の資料では、現時点で推奨される鍵長に加え、将来的に西暦何年までは何ビットの鍵長が必要か、さらにその後はどれくらいの鍵長があったほうが良いかが記載されている。

年代	推奨されるビット安全性
～2030年	112
2031年～	128, 192, 256

つまり、 2019 年現在は最低でも 112 ビット安全性を持たせておけば、ひとまず安心ということらしい。
たとえば RSA 暗号を使う場合は、鍵を 2048 ビットで作成すれば 112 ビット安全性は確保できることになる。

※あくまで解読計算量だけを見た場合の話であって、アルゴリズム自体に脆弱性が見つかった場合は別

鍵の生成

鍵は推測困難な値であることが望まれる。

人間が適当に値を選択すると、ランダムなつもりでも何かしらの偏りが発生する可能性がある。
したがって、鍵の生成には疑似乱数生成器という乱数（ランダムな値）を生成する仕組みを使用する。

パスワードベース暗号

疑似乱数生成器で生成された鍵は、ランダムで大きな数字の羅列になる。
これを人間が記憶しておくことはまずできない。

しかし、場合によっては人間が記憶できるフレーズを鍵として利用したくなることがある（後述の PKCS#12 など）。
ただ、人間が記憶できるフレーズではサイズが小さすぎて安全性が確保できない。

パスワードベース暗号（password based encryption : PBE）では、パスワード（人間が記憶できるフレーズ）を元に鍵を生成し、暗号化と復号に利用する。

具体的には次のような手順でパスワードから鍵を生成する。

1. ランダムな値（ソルト）を生成する
2. パスワードとソルトを連結してハッシュ値を計算する
3. 生成したハッシュ値をさらに何度か繰り返しハッシュ化する（ストレッチング or イテレーション）

最終的に生成されたハッシュ値を鍵として利用する。

ハッシュ値自体は暗号化が済んだら破棄し、ソルトだけを記録しておく。

もう一度同じ鍵が必要になった場合は、改めてパスワードの入力を求めるようにする。
そうすれば、保存しておいたソルトを利用することで再び同じ鍵を得ることができる。

ソルトとは

パスワードからそのままハッシュ値を計算して鍵とした場合、辞書攻撃に対して脆弱になる危険性がある。

辞書攻撃とは、パスワードに使われそうなフレーズがあらかじめ大量に登録されている辞書を利用する攻撃方法で、うまくいくと総当たり攻撃よりも大幅に少ない試行回数で攻撃を成功させることができる。

ランダムな値であるソルトを加えると事前にフレーズを準備することができなくなり、辞書攻撃を回避できる。

RFC8018

PBE の仕様は、最初は PKCS #5 として策定されていた（ver 1.5）。
その後、管理が IETF に移管され ver 2.0 が RFC2898 として策定された。

現在の最新は RFC8018 となっている。

ソルトのサイズ

ソルトのサイズは、最低でも 64 ビットを推奨している。

It should be at least eight octets (64 bits) long.
（訳）
それ（ソルト）は、最低でも 8 オクテット（64 ビット）の長さであるべきです。

4.1. Salt

イテレーション回数

イテレーションを $n$ 回実施すると、セキュリティ強度は $log_2 n$ ビットだけ上昇する。

イテレーション回数を何回にすべきかは、実行環境の性能やアプリケーションの特性によって異なってくる。

NIST の勧告では、処理時間をユーザが許容できるのであれば、可能な限りイテレーション回数は大きくすべきとしている。
最低でも 1000 回はイテレーションすべきだが、システムの性能や要件によっては 10,000,000 回が適切な場合もある、としている。

PBKDF1 と PBKDF2

RFC8018 では、パスワードとソルトから鍵を生成するための手法を２つ定義している。
それぞれ PBKDF1 と PBKDF2 と呼ばれる。

PBKDF1 はハッシュ関数を用いて鍵を生成する方法で、 MD5 や SHA-1 などを使う。
これは互換性のために残されているもので、新規に利用すべきではない。

一方、PBKDF2 は擬似乱数関数を用いて鍵を生成する方法で、新規に利用する場合はこちらが推奨されている。
具体的な疑似乱数関数として、 RFC8018 では HMAC が紹介されている（ハッシュには SHA-1 または SHA-2 を使用）。
HMAC 自体はメッセージ認証コードだが、擬似乱数関数としての性質も備えているらしい。
（暗号論的疑似乱数生成器もハッシュを使っているので、本質的には一緒ということだと思う、たぶん）

鍵の管理

鍵の寿命

鍵には、通信の際に一度だけ生成されてすぐに捨てられるようなものもあれば、一度生成されたあとも長期間利用する鍵もある。

前者は、ハイブリッド暗号で使用する秘密鍵などが該当する。
一方後者は、公開鍵暗号の鍵ペアなどが該当する。

このような寿命の長い鍵は、漏洩しないように適切に管理しなければならない。

鍵の鍵

秘匿する鍵が増えると、それだけ管理のコストが高くなる。

万が一鍵が漏洩しても大丈夫なようにするため、複数の鍵を別の１つの鍵（マスター鍵）で暗号化して保存することが考えられる。
この場合、管理者はマスター鍵を秘匿しておけばよくなり、複数の鍵を秘匿するよりは管理コストを減らすことができる。
（暗号化後の鍵も、もちろん可能な限り秘匿しておく）

PKCS#12

鍵をやり取りするときに使用するファイルフォーマットの仕様は RFC7292 で標準化されている。

これはもともと PKCS#12 という名前で規格されていたが、現在は IETF に管理が移管されているっぽい。
PKCS は Public-Key Cryptography Standards の略で、 RSA セキュリティ という会社が策定した公開鍵暗号に関する規格の集合になる（RSA セキュリティは RSA 暗号の考案者らが設立した会社）。

ファイル自体は公開鍵暗号、またはパスワードベース暗号で暗号化されるようになっている。

JDK に組み込まれている鍵を管理するための keytool という CUI ツールは、鍵の情報を PKCS#12 形式のファイルに保存して管理するようになっている（JDK 9 以降）。

乱数

暗号技術では、いたるところでランダムな値（乱数）を使用する。
乱数の生成もまた、暗号技術の重要な要素となっている。

乱数の性質

乱数には大きく３つの性質がある。

1. 無作為性
   • 乱数に偏りが無いこと
   • より「でたらめ」であること
2. 予測不可能性
   • 次の数が予測できないこと
   • 乱数の一部から別の部分を推測できないこと
3. 再現不可能性
   • 一度生成された乱数を再度生成できないこと

これらの性質は、数字が大きいものほどより強い乱数といえる。
つまり、予測不可能性を持った乱数は無作為性も持っていると言え、再現不可能性を持つ乱数は予測不可能性も持つと言える。

真の乱数

再現不可能性を持つ乱数は真の乱数と呼ばれる。

真の乱数は、再現不可能な自然現象をもとに生成される。
例えば、周辺環境の熱雑音の変化などが用いられる。

CPU によっては、ハードウェア的に再現不可能な乱数を生成する仕組みが組み込まれているものもある。

疑似乱数

再現不可能性を持たない乱数は、疑似乱数と呼ばれる。

ソフトウェアで生成される乱数は、何らかの初期値と特定のアルゴリズムによって作られるため、再現不可能性を持つことはできない。
したがって、ソフトウェアで生成される乱数は擬似乱数となる。

暗号で使用する乱数

暗号で使用する乱数は、最低でも予測不可能性を持っていなければならない。

再現不可能性まて持っていれば理想的だが、真の乱数の生成はコストが掛かることが多いため、実際は予測不可能性を持った疑似乱数が基本的に利用される。

Java には乱数を生成するためのクラスとして java.util.Random クラスが存在する。
このクラスが生成する乱数は無作為性は満たしているが、予測不可能性は満たしていない。

Java の場合、予測不可能性を持った疑似乱数生成器として java.security.SecureRandom というクラスが用意されている。

疑似乱数生成器の仕組み

疑似乱数を生成するソフトウェアを疑似乱数生成器と呼ぶ。

疑似乱数生成器の基本的な仕組みは次のようになっている。

1. 初期値となる値（シード）を入力として受け取る
2. シードを使って内部状態を初期化する
3. 内部状態をもとに乱数を生成する
4. 内部状態を更新する

以後は、乱数を生成するたびに３と４を繰り返すことになる。

シードや内部状態がわかると生成される乱数が推測できてしまうため、これらの値は攻撃者に知られないようにしなければならない。

特にシードがわかると、その後生成される乱数が分かってしまうため、推測困難な値にしなければならない。
このため、シードには真の乱数を用いることが多い。

ハッシュを使って疑似乱数を生成する

予測困難性を持った疑似乱数生成器を実現するための方法として、ハッシュ関数を利用するものがある。

この疑似乱数生成器は内部状態としてカウンタを持ち、カウンタのハッシュ値を乱数として出力する。
乱数を出力したら内部状態のカウンタを１つ加算して、次の乱数生成に使用する。
内部状態のカウンタは、ランダムなシートで初期化する。

この疑似乱数生成器が出力する次の乱数を予測するためには、現在の内部状態を知る必要がある。
ヒントとなるのは出力された値（ハッシュ値）だが、ハッシュ値から元の値を求めるのことはハッシュ関数の一方向性により困難となっている。

（あらかじめ様々な値からハッシュ値を得ていれば、いくつかの出力結果からカウンタを推測できてしまいそうだけど、カウンタの値を大きくしたり、ハッシュ値を一分だけを出力に利用するとかして回避するのかな？）

ハッシュ関数以外にも暗号化処理を利用する方法もある。

参考

• 暗号技術入門 第3版　秘密の国のアリス | 結城 浩 | コンピュータ・IT | Kindleストア | Amazon
• 暗号技術のすべて | IPUSIRON |本 | 通販 | Amazon
• 暗号利用モード - Wikipedia
• ブロック暗号 - Wikipedia
• ストリーム暗号 - Wikipedia
• Data Encryption Standard - Wikipedia
• Advanced Encryption Standard - Wikipedia
• ハッシュ関数 - Wikipedia
• 暗号学的ハッシュ関数 - Wikipedia
• Secure Hash Algorithm - Wikipedia
• SHA-1 - Wikipedia
• SHA-2 - Wikipedia
• SHA-3 - Wikipedia
• オイラーの関数の性質|思考力を鍛える数学
• RSA公開鍵暗号アルゴリズムを理解する
• 「電子署名=『秘密鍵で暗号化』」という良くある誤解の話 - Togetter
• 「電子署名=『秘密鍵で暗号化』」という良くある誤解の話 - Qiita
• 高木浩光＠自宅の日記 - 公開鍵暗号方式の誤り解説の氾濫をそろそろどげんかせんと
• 楕円曲線暗号 - Wikipedia
• ディフィー・ヘルマン鍵共有 - Wikipedia
• RSA暗号 - Wikipedia
• ElGamal暗号 - Wikipedia
• 公開鍵暗号 | シニアエンジニアの庵

1. Private Key は「秘密鍵」または「非公開鍵」と訳されることもある。しかし、「秘密鍵」は共通鍵暗号の Secret Key と混同する恐れがあり、「非公開鍵」は「公開鍵」と誤読する可能性を考慮して、ここでは「プライベート鍵」の表記で統一する。 ↩

2. 剰余演算のことをモジュロ（modulo）と呼び、「法」はモジュロを日本語訳した言葉になる ↩

3. さらっと書いてるけど、実際はしらみつぶしに頑張って探した ↩

4. 厳密には単純にハッシュ化するだけなく、ソルトの追加やストレッチングなどを行う。詳しくは BCryptのすすめ - Qiita などを参照。 ↩

5. そのまま「えすえいちえー」って読んでた ↩

6. プライベート鍵が漏洩したり、不正な証明書を発行したなど様々な理由が考えられる ↩