はじめに
変分推論の手法の1つであるNormalizing Flowを実装しました.
ベイズ線形回帰の話から始めて,従来の変分推論,Normalizing Flowによる変分推論という流れで理論を述べています.
実装したコードはGitHubにあります.
ベイズ線形回帰
線形回帰では以下のように,観測データ$\boldsymbol x$に対して予測値$\boldsymbol y$を出力します.$\boldsymbol \theta$はパラメータで単回帰の場合では直線の傾きに相当します.
$$\boldsymbol y=\boldsymbol \theta^T\boldsymbol x \tag{1}$$
ただ,実際の値はノイズを含んでいるため,それをモデル化するために以下のように平均が$\boldsymbol y$,共分散が$I$のガウス分布に従うものとします.(e.g. 温度計で温度を計測した場合の機器誤差.)
$$p(\boldsymbol y \mid \boldsymbol x,\boldsymbol \theta)=\mathcal{N}(\boldsymbol y\mid \boldsymbol \theta^T\boldsymbol x, I) \tag{2}$$
ここで,上式を使って未観測データに対する回帰予測を行うためには,最適なパラメータ$\boldsymbol \theta$を決定する必要があります.通常の線形回帰(非ベイズ)では$\boldsymbol \theta$はある1つに定まる値ですが,ベイズでは$\boldsymbol \theta$の確率分布を考えます.すなわち,既に手元にあるデータ$\boldsymbol X^{(train)}$と$\boldsymbol y^{(train)}$から最適なパラメータ$\boldsymbol \theta$の確率分布$p(\boldsymbol \theta \mid \boldsymbol X^{(train)}, \boldsymbol y^{(train)})$を決定します.$p(\boldsymbol \theta \mid \boldsymbol X^{(train)}, \boldsymbol y^{(train)})$を求めるためには以下のベイズの定理を用います.
$$
p(\boldsymbol \theta \mid \boldsymbol X^{(train)},\boldsymbol y^{(train)})=
\cfrac{p(\boldsymbol y^{(train)} \mid \boldsymbol X^{(train)}, \boldsymbol \theta)p(\boldsymbol \theta)}{p(\boldsymbol y^{(train)} \mid \boldsymbol X^{(train)})}
\tag{3}
$$
$p(\boldsymbol \theta \mid \boldsymbol X^{(train)}, \boldsymbol y^{(train)})$は事後分布と呼ばれており,これが求まれば以下の式を使って未知データ$\boldsymbol X^{(new)}$に対する予測値$\boldsymbol y^{(new)}$が計算できます.
$$
p(\boldsymbol y^{(new)}\mid \boldsymbol X^{(new)}, \boldsymbol y^{(train)}, \boldsymbol X^{(train)})=
\int p(\boldsymbol y^{(new)}\mid \boldsymbol X^{(new)},\boldsymbol \theta)
p(\boldsymbol \theta \mid \boldsymbol y^{(train)}, \boldsymbol X^{(train)})
d\boldsymbol \theta
$$
実際に事後分布を求めるためにベイズの定理(3)式を詳しく見てくと,まず分子の尤度$p(\boldsymbol y^{(train)} \mid \boldsymbol X^{(train)}, \boldsymbol \theta)$は既に(2)式でモデル化済みなので計算可能です.
同じく分子の事前分布$p(\boldsymbol \theta)$は設計者が自由にモデル化可能です.(通常は共益事前分布と呼ばれる特定の分布を使用するようです.)
最後に周辺尤度$p(\boldsymbol y^{(train)} \mid \boldsymbol X^{(train)})$は次式から計算します.
$$
p(\boldsymbol y^{(train)} \mid \boldsymbol X^{(train)})=
\int p(\boldsymbol y^{(train)} \mid \boldsymbol X^{(train)}, \boldsymbol \theta)p(\boldsymbol \theta)d\boldsymbol \theta
\tag{4}
$$
線形回帰のような簡単なタスクであれば解析的に計算可能ですが,モデルが複雑になると積分を計算することは困難になります.そこで使われる手法が変分推論です.
変分推論
周辺尤度を解析的に厳密に計算することを回避し,求めたい事後分布$p(\boldsymbol z \mid \boldsymbol x)$をある確率分布$q(\boldsymbol z)$によって近似しようというアイデアが変分推論です.(論文に表記を合わせるため,パラメータ$\boldsymbol \theta$を$\boldsymbol z$と記述しています.)
変分推論の一例として平均場近似という,近似事後分布$q(\boldsymbol z)$に対して,確率変数の独立性を仮定し,確率分布を分解するという手法があります.
$$q(\boldsymbol z)=\prod_{i} q(\boldsymbol z_i) \tag{5}$$
そしてこの確率分布$q(\boldsymbol z)$を真の事後分布$p(\boldsymbol z \mid \boldsymbol x)$と近しいものにするために,$z$に対して最適化を行います.
(最適化式を全て導出するのは大変なので)天下りになってしまいますが,次式が成り立つことが知られています.
$$
\ln p(\boldsymbol x)-\int q(\boldsymbol z)\ln \frac{p(\boldsymbol x, \boldsymbol z)}{q(\boldsymbol z)}d\boldsymbol z
=KL(q(\boldsymbol z)|p(\boldsymbol z \mid \boldsymbol x))
\tag{6}
$$
上式のKLはKL Divergenceと呼ばれる2つの分布間の距離の指標です.$\ln p(\boldsymbol x)$の部分は$z$に依らない定数なので,左辺第二項だけを最小化すれば2つの分布間の距離(=右辺のKL Dirvergence)を最小化できることになります!(ちなみに左辺第二項はの負値はELBO(Evidence Lower Bound)と呼ばれています.)
これで最適化(ELBOの最大化)によって近似事後分布を求めることができるのですが,そもそも(5)式の仮定には問題があります.(5)式のような独立性を仮定することにより,変数間に存在する相関を考慮することができず,表現力の乏しい確率分布になってしまい,真の事後分布を表現することができないようです.
この表現力の乏しさを解決する手法がNormalizing Flowです.
Normalizing Flow
Normalizing Flowはガウス分布等の単純な確率分布$q(\boldsymbol z)$に従う確率変数$\boldsymbol z$に対して,非線形変換$f$を重ねることで複雑な分布$q_k(\boldsymbol z_k)$を得ようというアイデアです.
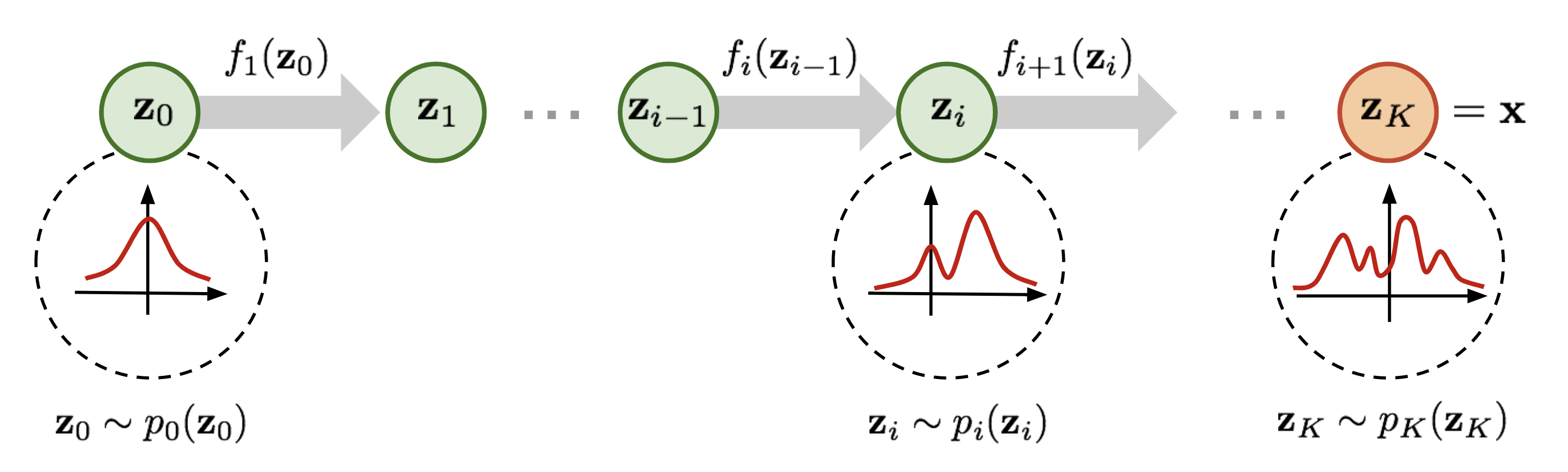
引用元 : L.Weng. "Flow-based Deep Generative Model
確率分布$q(\boldsymbol z)$に従う確率変数$\boldsymbol z$に対して,非線形変換$f$を作用させると(7)式と(8)式が得られます.$z$は多変数なので右辺に登場する微分はヤコビアンであり.detは行列式を意味します.
$$\boldsymbol z'=f(\boldsymbol z)\tag{7}$$
$$q'(\boldsymbol z')=q(\boldsymbol z)\left|
\det \frac{\partial f}{\partial \boldsymbol z'}\right|^{-1} \tag{8}$$
この非線形変換を複数回重ねることで,確率分布はより複雑で表現力の高いものとなっていきます.
$$
\boldsymbol z_k=f_k\circ \cdots \circ f_2 \circ f_1(\boldsymbol z_0) \tag{9}
$$
$$
q_k(\boldsymbol z_k)=q_0(\boldsymbol z_0)\prod_{k=1}^{K}
\left| \det \frac{\partial f_k}{\partial \boldsymbol z_{k-1}}\right|^{-1} \tag{10}
$$
非線形関数$f_k$の選び方ですが全単射の関数,すなわち逆関数が計算できる非線形関数であればOKみたいです.論文中では非線形関数$f_k$としてplanar flowというものが紹介されています.
planar flowは以下のような関数です(シンプルなResidul Blockのようなものですね).$\boldsymbol u, \boldsymbol w, b$はパラメータであり,学習によって値が更新されます.$h$は活性化関数であり,tanhを用います.
$$
f(\boldsymbol z)=\boldsymbol z + \boldsymbol u h(\boldsymbol w^T \boldsymbol z + b) \tag{11}
$$
上式の関数を用いることでヤコビアンの行列式が以下のように解析的に計算できます.
$$
\left| \det \frac{\partial f(\boldsymbol z)}{\partial \boldsymbol z}\right|
=\left| 1+\boldsymbol u^T \psi(\boldsymbol z)\right| \tag{12}
$$
ただし,$\psi(\boldsymbol z)$は次式から計算されます.
$$
\psi(\boldsymbol z)=h'(\boldsymbol w^T \boldsymbol z+b)\boldsymbol w \tag{13}
$$
これにより(10)式を計算できるようになり,変換後の確率分布が求まるようになりました!
$$
q_k(\boldsymbol z_k)=q_0(\boldsymbol z_0)\prod_{k=1}^{K}
\left| 1+\boldsymbol u_k^T \psi_k(\boldsymbol z_k)\right|^{-1}
\tag{13}
$$
(13)式にはベクトルの内積と絶対値と逆数の計算しか行わないので,計算コストが非常に小さいことが分かるかと思います.
次は(13)式によって得られた確率分布を真の事後分布に近づけるための最適化式の導出です.先程の変分推論手法(平均場近似)と同様に,Normalizing FlowもELBOを最大化することで最適化を行います.
\mathcal{L}(\boldsymbol{x})=
\int q(\boldsymbol z)\ln \frac{p(\boldsymbol x, \boldsymbol z)}{q(\boldsymbol z)}d\boldsymbol z\\
=\mathbb{E}_{q(\boldsymbol z)}[\ln p(\boldsymbol x, \boldsymbol z) - \ln q(\boldsymbol z)]\\
=\mathbb{E}_{q_k(\boldsymbol z_k)}[\ln p(\boldsymbol x, \boldsymbol z_k) - \ln q(\boldsymbol z_k)]\\
\sim \sum_{l=1}^{L}[\ln p(\boldsymbol{x}, \boldsymbol{z_k^{(l)}})-\ln q(\boldsymbol{z_k^{(l)}})]
\tag{14}
$\boldsymbol{z_k^{(l)}}$はミニバッチに含まれる$l$番目のサンプル$\boldsymbol{z^{(l)}}$を(9)式によって$k$回だけ非線形変換したものです.
実装する際には最大化よりも最小化の方が都合が良いため,ELBOにマイナスを掛けた次式を最小化します.
$$
-\mathcal{L}(\boldsymbol{x})=\sum_{l=1}^{L}[\ln q(\boldsymbol{z_k^{(l)}}) - \ln p(\boldsymbol{x}, \boldsymbol{z_k^{(l)}})] \tag{15}
$$
実行環境
Python 3.7.5
TensorFlow 1.15.0
実装
初期分布であるガウス分布をPlanar flowによる非線形変換によって目標の複雑な分布を再現していきます.(左が初期分布となるガウス分布,中央と右が目標の分布です).
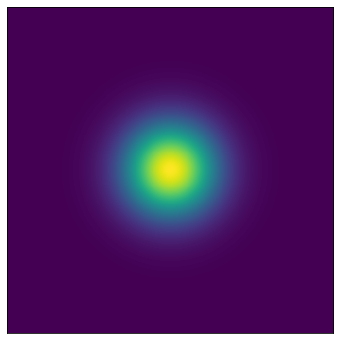
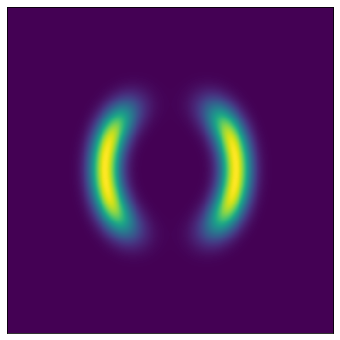
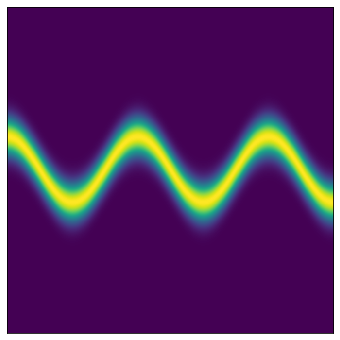
まずplanar flowから実装していきます.損失関数を計算する際には$\ln q_k(\boldsymbol z_k)$が必要になるので,ここで計算しています.
class PlanarFlow:
def __init__(self, dim):
self.dim = dim
self.h = lambda x: tf.tanh(x)
self.h_prime = lambda x: 1 - tf.tanh(x)**2
self.w = tf.Variable(tf.random.truncated_normal(shape=(1, self.dim)))
self.b = tf.Variable(tf.zeros(shape=(1)))
self.u = tf.Variable(tf.random.truncated_normal(shape=(1, self.dim)))
def __call__(self, z, log_q):
z = z + self.u*self.h(tf.expand_dims(tf.reduce_sum(z*self.w, -1), -1) + self.b)
psi = self.h_prime(tf.expand_dims(tf.reduce_sum(z*self.w, -1), -1) + self.b)*self.w
det_jacob = tf.abs(1 + tf.reduce_sum(psi*self.u, -1))
log_q = log_q - tf.log(1e-7 + det_jacob)
return z, log_q
次にplanar flowをK個重ねることでNormalizing Flowを構成します.
class NormalizingFlow:
def __init__(self, K, dim):
self.K = K
self.dim = dim
self.planar_flow = [PlanarFlow(self.dim) for i in range(self.K)]
def __call__(self, z_0, log_q_0):
z, log_q = self.planar_flow[0](z_0, log_q_0)
for pf in self.planar_flow[1:]:
z, log_q = pf(z, log_q)
return z, log_q
そして損失関数(15)式を以下のように計算します.ここでtarget_densityは目標となる確率分布です.
最適化手法にはAdamを使用しています.
placeholderを取得する関数も定義しておきます.
def calc_loss(z_k, log_q_k, target_density):
log_p = tf.log(target_density.calc_prob_tf(z_k)+1e-7)
loss = tf.reduce_mean(log_q_k - log_p, -1)
return loss
def get_train(loss):
return tf.train.AdamOptimizer().minimize(loss)
def get_placeholder():
z_0 = tf.placeholder(tf.float32, shape=[None, 2])
log_q_0 = tf.placeholder(tf.float32, shape=[None])
return z_0, log_q_0
上記のクラスと関数を使って計算グラフの構築を行います.
normalizing_flow = NormalizingFlow(K=16, dim=2)
z_0, log_q_0 = get_placeholder()
z_k, log_q_k = normalizing_flow(z_0, log_q_0)
loss = calc_loss(z_k, log_q_k, target_density)
train = get_train(loss)
確率的勾配降下法を使って学習を行います.ミニバッチサイズは1000サンプル,訓練回数は10万回としています.
with tf.Session() as sess:
invisible_axis = True
sess.run(tf.global_variables_initializer())
for iteration in range(100000+1):
z_0_batch = normal_distribution.sample(1000)
log_q_0_batch = np.log(normal_distribution.calc_prob(z_0_batch))
_, loss_value = sess.run([train, loss], {z_0:z_0_batch, log_q_0:log_q_0_batch})
結果がこちらになります.ガウス分布からスタートして複雑な分布のサンプリングが正しく行えていることが分かります.
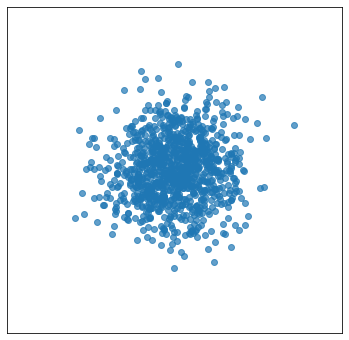


全実装
最後に全ての実装をまとめたものを以下に載せておきます.main.py,normalizing_flow.py, distribution.pyの3種類があります.main.pyは計算グラフを構築し学習を実行するためのファイル,normalizing_flow.pyは計算グラフを構築するためのモデルの定義や損失関数の定義を行うファイル,最後にdistribution.pyは確率分布のサンプリングや確率の計算を行うための機能を持つファイルです.
GitHubにもファイルを載せておきます.
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from distribution import *
from normalizing_flow import *
normal_distribution = NormalDistribution2D()
target_density = TargetDistribution1()
normalizing_flow = NormalizingFlow(K=16, dim=2)
z_0, log_q_0 = get_placeholder()
z_k, log_q_k = normalizing_flow(z_0, log_q_0)
loss = calc_loss(z_k, log_q_k, target_density)
train = get_train(loss)
with tf.Session() as sess:
invisible_axis = True
sess.run(tf.global_variables_initializer())
for iteration in range(100000+1):
z_0_batch = normal_distribution.sample(1000)
log_q_0_batch = np.log(normal_distribution.calc_prob(z_0_batch))
_, loss_value = sess.run([train, loss], {z_0:z_0_batch, log_q_0:log_q_0_batch})
if iteration % 100 == 0:
print('Iteration : {} Loss : {}'.format(iteration, loss_value))
if iteration % 10000 == 0:
z_k_value = sess.run(z_k, {z_0:z_0_batch, log_q_0:log_q_0_batch})
plt.figure(figsize=(6, 6))
plt.scatter(z_k_value[:, 0], z_k_value[:, 1], alpha=0.7)
if invisible_axis:
plt.tick_params(bottom=False,left=False,right=False,top=False)
plt.tick_params(labelbottom=False,labelleft=False,labelright=False,labeltop=False)
plt.show()
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
def get_placeholder():
z_0 = tf.placeholder(tf.float32, shape=[None, 2])
log_q_0 = tf.placeholder(tf.float32, shape=[None])
return z_0, log_q_0
def calc_loss(z_k, log_q_k, target_density):
log_p = tf.log(target_density.calc_prob_tf(z_k)+1e-7)
loss = tf.reduce_mean(log_q_k - log_p, -1)
return loss
def get_train(loss):
return tf.train.AdamOptimizer().minimize(loss)
class PlanarFlow:
def __init__(self, dim):
self.dim = dim
self.h = lambda x: tf.tanh(x)
self.h_prime = lambda x: 1 - tf.tanh(x)**2
self.w = tf.Variable(tf.random.truncated_normal(shape=(1, self.dim)))
self.b = tf.Variable(tf.zeros(shape=(1)))
self.u = tf.Variable(tf.random.truncated_normal(shape=(1, self.dim)))
def __call__(self, z, log_q):
z = z + self.u*self.h(tf.expand_dims(tf.reduce_sum(z*self.w, -1), -1) + self.b)
psi = self.h_prime(tf.expand_dims(tf.reduce_sum(z*self.w, -1), -1) + self.b)*self.w
det_jacob = tf.abs(1 + tf.reduce_sum(psi*self.u, -1))
log_q = log_q - tf.log(1e-7 + det_jacob)
return z, log_q
class NormalizingFlow:
def __init__(self, K, dim):
self.K = K
self.dim = dim
self.planar_flow = [PlanarFlow(self.dim) for i in range(self.K)]
def __call__(self, z_0, log_q_0):
z, log_q = self.planar_flow[0](z_0, log_q_0)
for pf in self.planar_flow[1:]:
z, log_q = pf(z, log_q)
return z, log_q
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
class Distribution:
def calc_prob(self, z):
p = np.zeros(z.shape[0])
return p
def plot(self, size=5):
side = np.linspace(-size, size, 1000)
z1, z2 = np.meshgrid(side, side)
shape = z1.shape
z1 = z1.ravel()
z2 = z2.ravel()
z = np.c_[z1, z2]
probability = self.calc_prob(z).reshape(shape)
plt.figure(figsize=(6, 6))
plt.imshow(probability)
plt.tick_params(bottom=False,left=False,right=False,top=False)
plt.tick_params(labelbottom=False,labelleft=False,labelright=False,labeltop=False)
plt.show()
class NormalDistribution2D(Distribution):
def sample(self, sample_num):
z = np.random.randn(sample_num, 2)
return z
def sample_tf(self, sample_num):
z = tf.random_normal([sample_num, 2])
return z
def calc_prob(self, z):
p = np.exp(-(z[:, 0]**2+z[:, 1]**2)/2)/(2*np.pi)
return p
def calc_prob_tf(self, z):
p = tf.exp(-(z[:, 0]**2+z[:, 1]**2)/2)/(2*np.pi)
return p
class TargetDistribution1(Distribution):
def calc_prob(self, z):
z1, z2 = z[:, 0], z[:, 1]
norm = np.sqrt(z1**2+z2**2)
exp1 = np.exp(-0.5*((z1-2)/0.6)**2)
exp2 = np.exp(-0.5*((z1+2)/0.6)**2)
p = 0.5*((norm - 2)/0.4)**2 - np.log(exp1 + exp2)
return np.exp(-p)
def calc_prob_tf(self, z):
z1, z2 = z[:, 0], z[:, 1]
norm = tf.sqrt(z1**2+z2**2)
exp1 = tf.exp(-0.5*((z1-2)/0.6)**2)
exp2 = tf.exp(-0.5*((z1+2)/0.6)**2)
p = 0.5*((norm - 2)/0.4)**2 - tf.log(exp1 + exp2)
return tf.exp(-p)
class TargetDistribution2(Distribution):
def calc_prob(self, z):
z1, z2 = z[:, 0], z[:, 1]
w1 = np.sin(0.5*np.pi*z1)
p = 0.5*((z2 - w1)/0.4)**2
return np.exp(-p)
def calc_prob_tf(self, z):
z1, z2 = z[:, 0], z[:, 1]
w1 = tf.sin(0.5*np.pi*z1)
p = 0.5*((z2 - w1)/0.4)**2
return tf.exp(-p)