A - Weekly Records
問題文
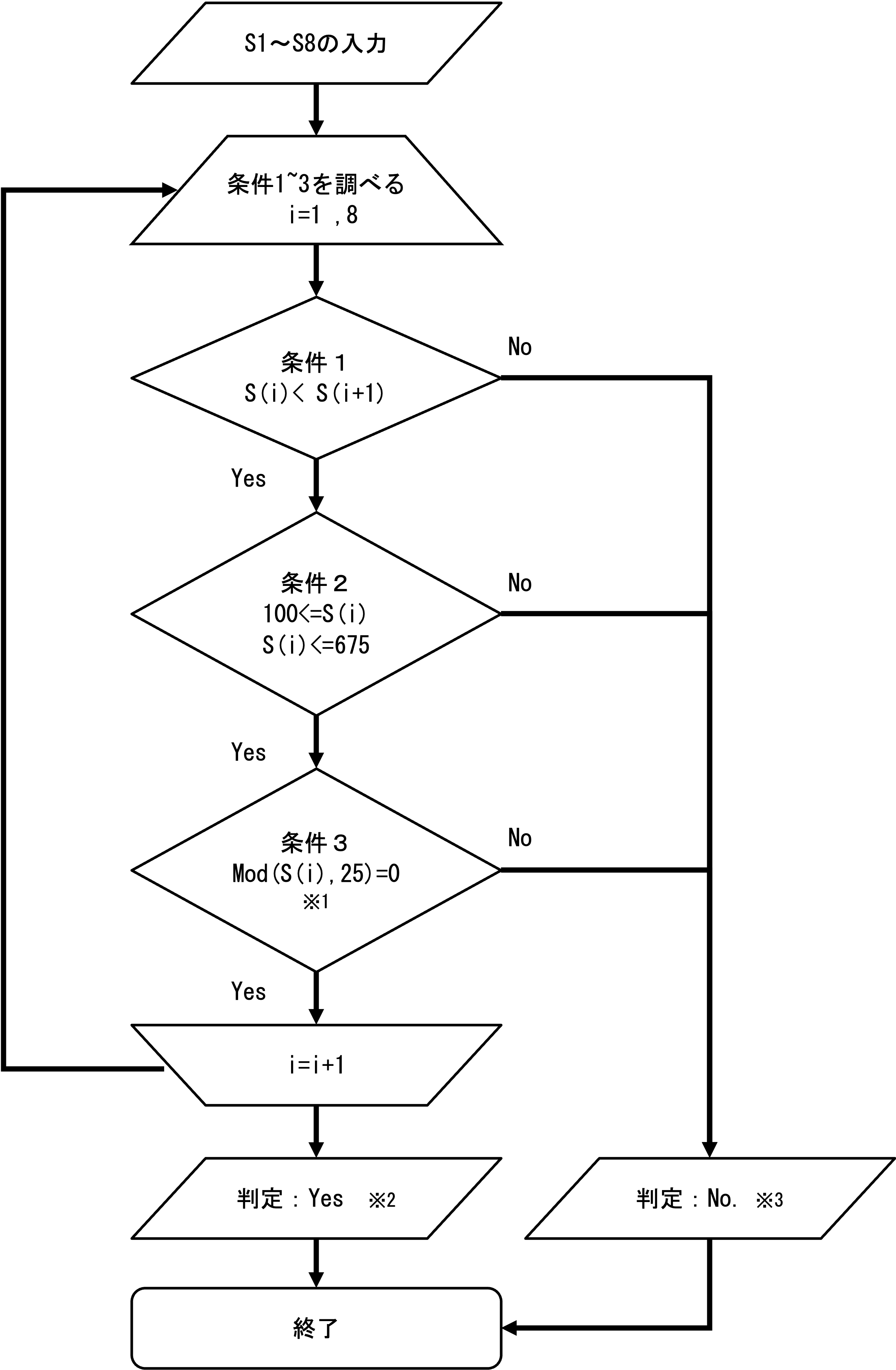
与えられた8個の整数について、以下の3つの条件を全て満たすかどうかにより、 Yes/Noを出力します。
- 数列 (S1,S 2,…,S8)はS1≤S2≤⋯≤S8ある。
- S1,S2,…,S8は全て100以上675以下である。
- S1,S2,…,S 8は全て25の倍数である。
詳細はこちらです。
解説
【補足】
※1
「25の倍数であるかどうか」については、25で割った余りが0かどうかにより判定します。
プログラムに実装する際には、mod関数を使用します。
※2
S1〜S8のの整数が条件1〜3を全て満たす場合、Do文を抜けられるためYesを出力します。
※3
S1〜S8のの整数が条件1〜3を1つでも満たさない事が判明した場合、その時点でNoを出力し、プログラムを終了します。
プログラム例
program ABC308a
implicit none
integer(8) i, j, tmp
integer(8) S(8)
!初期化
i = 0; j = 1; tmp = 0
!入力
read (*, *) S(:)
!処理
do i = 1, 8
!S(i)<S(i+1)
if (i < 8) then
if (S(i) > S(i + 1)) then
write (*, "(a)") 'No'
stop
end if
end if
if (S(i) > S(i + 1)) then
write (*, "(a)") 'No'
stop
end if
!S(i)が100以上 ,675以下
if (S(i) < 100 .or. S(i) > 675) then
write (*, "(a)") 'No'
stop
end if
!S(i)が25の倍数
if (mod(S(i), 25) /= 0) then
write (*, "(a)") 'No'
stop
end if
end do
!結果の出力
write (*, "(a)") 'Yes'
end
B - Default Price
問題文
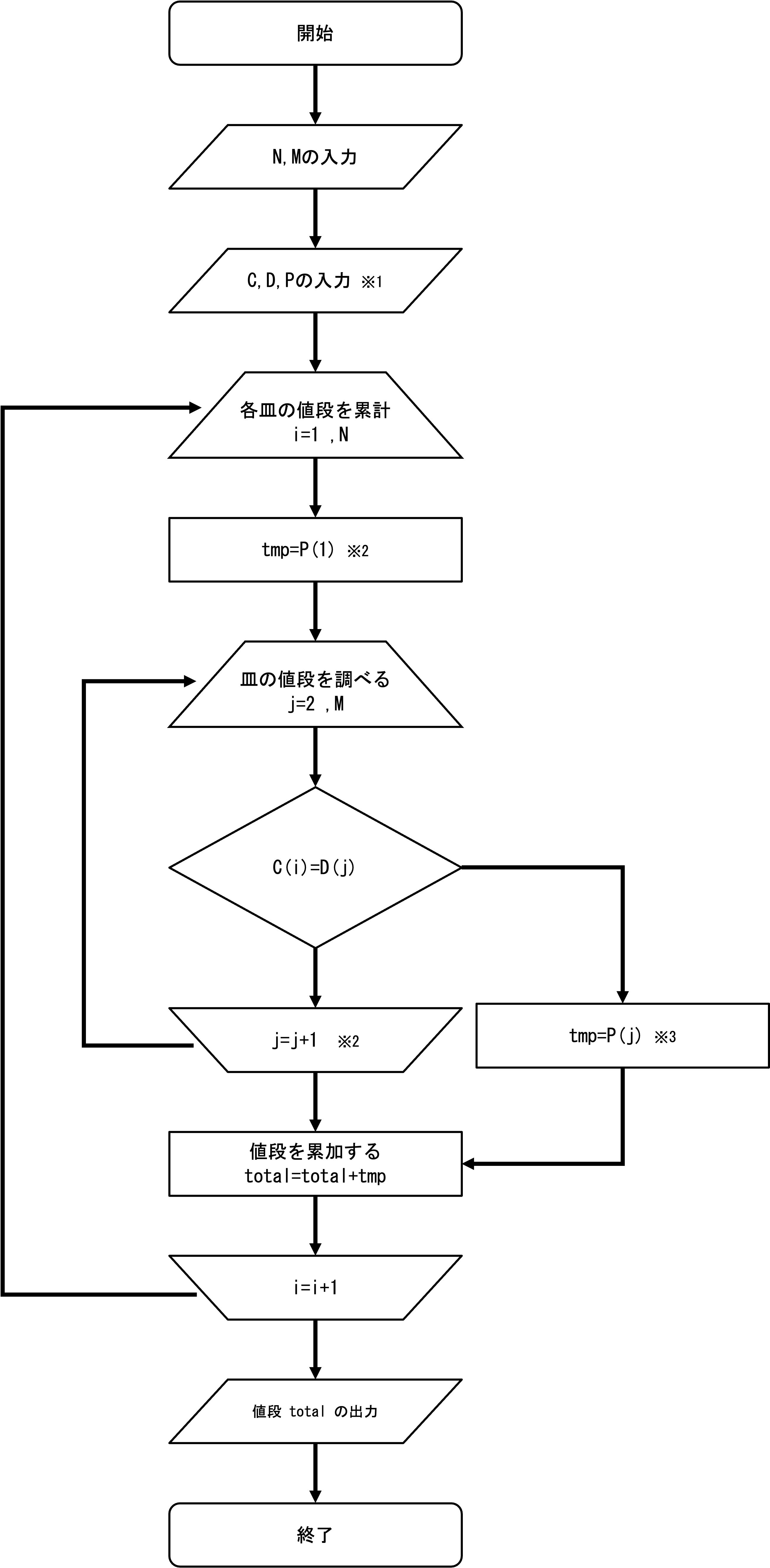
N皿食べた料理の合計金額を算出します。
料理の価格は皿の色と対応しますが、定義されていない色の皿が出てくる事に注意が必要です。
詳細はこちらです。
解説
【補足】
※1
Pは定義されていない色の皿の値段を格納するため、Mよりも1つ配列が大きくなります。
PとMについて、値段と色で配列の添え字がずれていると分かりにくいので、Mは1つ大きく配列を確保します。
P(1)に定義されていない色の皿の値段を格納します。
M(1)には何も格納しません。
※2
皿の色を調べ、一致すればtmpに単価を代入します。
どの色にも当てはまらない場合には、P(1)であるため、予めtmp=P(1)にしておきます。
一致する皿の色が見つかれば、tmpは上書きされるので問題ありません。
※3
一致する皿の色が見つかれば、tmpは上書きします。
また、これ以上は皿の色を調べる必要がないので、exit文によりdo文を抜けます。
プログラム例
program ABC308b
implicit none
integer(8) i, j, total, tmp
integer(8) N, M
character(20), allocatable :: C(:), D(:)
integer, allocatable :: P(:)
!初期化
i = 0; j = 0; total = 0; tmp = 0
!入力
read (*, *) N, M
M = M + 1 !対象外の皿の分があるので+1
allocate (C(N), D(M), P(M))
read (*, *) C(:)
read (*, *) (D(i), i=2, M)
read (*, *) P(:)
!処理
do i = 1, N
tmp = P(1)
do j = 2, M
if (C(i) == D(j)) then
tmp = P(j)
exit
end if
end do
total = total + tmp
end do
!結果の出力
write (*, "(i0)") total
end
C - Standings
問題文
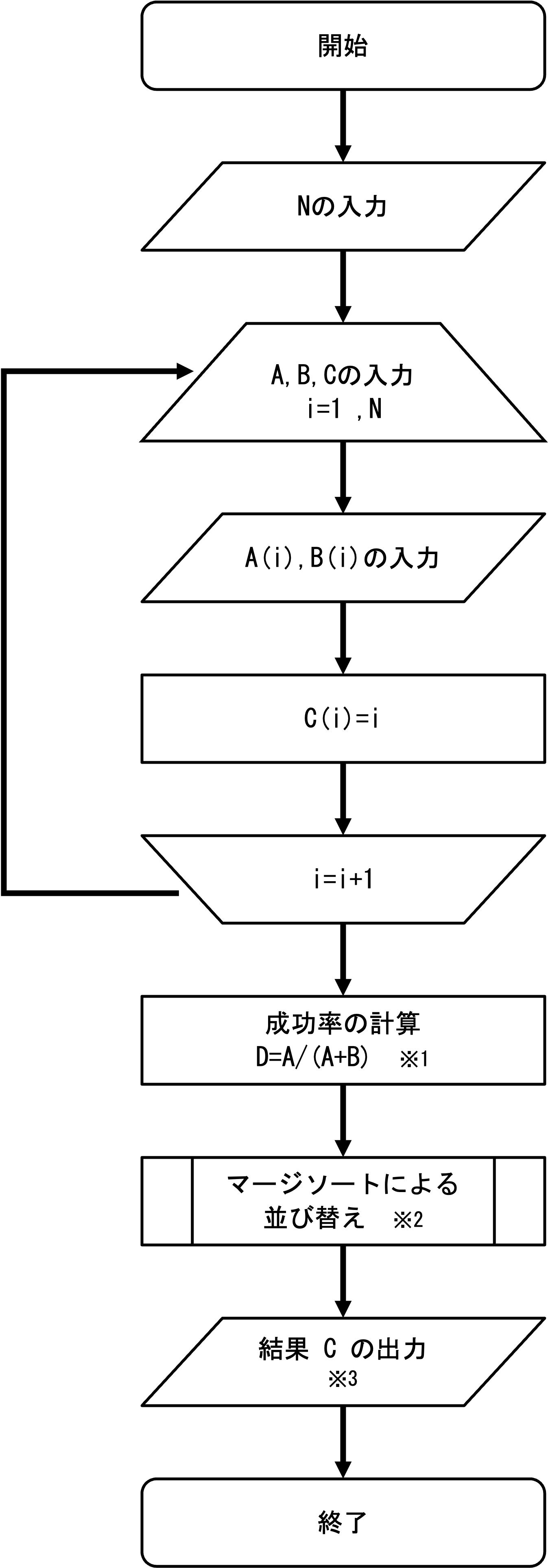
コイントスをしたN人のうち、表の確率が高い人から順に出力します。
確率が同じ場合には、番号が若い順に出力します。
詳細はこちらです。
解説
※1
Fortranでは配列の計算を一括で行う事ができます。
Do文でD(i)=A(i)/(A(i)+B(i))を適時計算せずとも、D=A/(A+B)で1からNのDをまとめて計算する事ができます。
また、AとBの値の範囲が$0 <= A,B <=10^9$と非常に大きくなる可能性があるため、桁落ちの可能性があります。
今回は4倍精度で変数を定義し、桁落ちを回避しました。
※2
計算したDを大きい順(成功率の高い順)に並び替えます。
この時、確率が同じ場合は番号が小さい順に並び替える必要があります。
順番は小さい順から既に格納されていますので、確率が同じ場合は並び替えをしない事が求められています。
従って並び替えのアルゴリズムは、安定ソートである事が必須です。
そこで今回は、マージソートにより並び替えを行いました。
※3
並び替えの結果を出力します。
確率が同じ場合には、番号が小さい順にから出力します。
プログラム例
module global_variable
integer(4) N
end module
program ABC308c
use global_variable
implicit none
real(16), allocatable :: A(:), B(:), D(:), tmp(:)
integer(16), allocatable :: C(:), tmp2(:)
integer(16) start, end, i
!初期化
i = 0
read (*, *) N
allocate (A(N), B(N), C(N), D(N))
allocate (tmp(N), tmp2(N))
!処理
do i = 1, N
read (*, *) A(i), B(i)
C(i) = i
end do
D = (A/(A + B))
start = 1; end = N
tmp = 0; tmp2 = 0
call margesort(D, C, tmp, tmp2, start, end)
!結果の出力
write (*, '(*(i0,1x))') C
end program
recursive subroutine margesort(x, y, tmp, tmp2, left, right)
integer(16) left, right, mid
integer(16) N
real(16) x(N), tmp(N)
integer(16) y(N), tmp2(N)
integer(16) i, j, k
!これ以上2分かつできないならretrun
if (left >= right) return
!分割できるだけ分割する
mid = (left + right)/2
call margesort(x, y, tmp, tmp2, left, mid)
call margesort(x, y, tmp, tmp2, mid + 1, right)
!並び替えの下準備としてtmpに配列をコピー
j = 0
tmp(left:mid) = x(left:mid)
tmp2(left:mid) = y(left:mid)
do i = mid + 1, right
tmp(i) = x(right - j)
tmp2(i) = y(right - j)
j = j + 1
end do
!大小比較して小さい順に入れていく
i = left
j = right
!write (*, '(3x,*(f13.101x),a)', advance='no') x(left:right)
!write (*, '(a)', advance='no') '>>'
do k = left, right
if (tmp(i) > tmp(j)) then
x(k) = tmp(i)
y(k) = tmp2(i)
i = i + 1
else if (tmp(i) == tmp(j) .and. tmp2(i) < tmp2(j)) then
x(k) = tmp(i)
y(k) = tmp2(i)
i = i + 1
else
x(k) = tmp(j)
y(k) = tmp2(j)
j = j - 1
end if
end do
!write (*, '(3x,*(f13.10,1x))') x(left:right)
end subroutine margesort
感想
- C問題について、約分や$10^{19}$を行うなどの工夫をし、桁落ちを回避する策がある様ですが、Fortranなら4倍変数で変数を用意すれば解決できます。
- フロー図を入れる事で、記事の見やすさが改善しました。(フロー図を書く練習がしたいので、今後も使用します。)