本記事はWACUL Advent Calendar 2017の12/3の記事になります。
こんにちは、株式会社WACULで、データ分析の仕事をしている@onhrsです。
今回は、今年を締めくくるにふさわしいであろう、世紀の大発見である"重力波"について解説します。また、その発見の裏で今流行のPythonが役立っていたことを述べ、最後にPythonで分析入門として、実際に手を動かして今回の大発見にについて触れてみたいと考えております。
まずはじめに
今回の記事を書いている私自身、宇宙物理や相対性理論に精通している訳では決っしてなく、ど素人が1〜2週間勉強した事による個人の解釈、見解によるものです。
個人的にサイエンスが好きなことと、現在業務で主に使用しているPythonが重力波解析に使われていた事に興味を持ち持ったため今回書こうと思いました。
今回の記事を作るにあたり、勉強した代表的な資料は以下になります。
重力波について
・重力波とはなにか 「時空のさざなみ」が拓く新たな宇宙論 (ブルーバックス)
実際の解析では
・BINARY BLACK HOLE SIGNALS IN LIGO OPEN DATA
以下のコードも参考にさせていただきました。
https://github.com/bakfoo/pyconjp2016/blob/master/ligo/gwave_pyconjp2016.ipynb
今回の記事をきっかけに、上記の本や、サイトなどでより本格的な分析するためのきっかけになればと思います。
重力波について
重力波とは英語版のwikipediaを一部抜粋し要約すると以下のようになります。
・重力波は、ある種の重力相互作用で発生し、光の速度でその源から外向きに波として伝播する、時空の歪みによって生じる波です。1905年にアンリ・ポアンカレによって最初に提案され、その後、それに続く形で、1916年にアルバート・アインシュタインによって相対性理論の一般的な理論に基づいて予言されました。
・重力波は、電磁放射と同様の放射エネルギーの一種である重力放射としてエネルギーを輸送します。
・ニュートンの古典力学の一部である普遍的な重力の法則は、その法則が物理的相互作用が無限の速度で伝播するという仮定、つまり古典物理学の方法が相対性理論に関連する現象を説明できない方法の1つを示しています。
上記の説明が、どういうことなのか見ていきましょう。
重力波は時空の歪みによって生じる波である
重力波に入る前に、そもそも重力とは何者かについてお話し致します。普段、我々の感じている重力というものは、物体間の万有引力によるものであると高校のとき物理を選択していた方は習ったと思います。
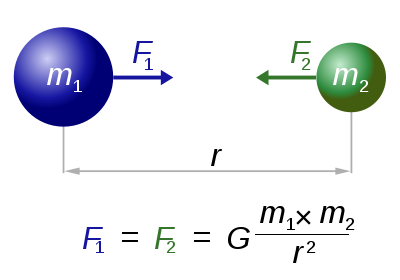
F=\frac{Gm_1m_2}{r^2}
$r$は距離で、$G$が重力定数、$m_1$,$m_2$が各物体(例えば、太陽と地球の場合は$M_1$が地球の質量、$M_2$が太陽の質量)
図はwikipediaの万有引力定数より
物体が大きくて距離が短ければ、大きく作用致します。ゆえに、質量の重い太陽では地球の約28倍、月では約0.165倍の重力が作用していると考えられています。
上記の考えは『りんごが落ちた定説』で有名なアイザック・ニュートンによって産み出され、今でもこの定理が正しいと考えられていますが、ニュートン自身なぜ万有引力という遠隔力が存在するのかということについて証明することができませんでした。
図はDid the apple really fall on Newton’s head?より
その後20世紀に入ると、アインシュタインによって、重力を4次元の時空(3次元の空間[x,y,z]+時間[t]))として解釈する一般相対性理論によって重力の概念が変更されました。
 [wikipedia アルベルト・アインシュタイン](https://ja.wikipedia.org/wiki/%E3%82%A2%E3%83%AB%E3%83%99%E3%83%AB%E3%83%88%E3%83%BB%E3%82%A2%E3%82%A4%E3%83%B3%E3%82%B7%E3%83%A5%E3%82%BF%E3%82%A4%E3%83%B3)より
[wikipedia アルベルト・アインシュタイン](https://ja.wikipedia.org/wiki/%E3%82%A2%E3%83%AB%E3%83%99%E3%83%AB%E3%83%88%E3%83%BB%E3%82%A2%E3%82%A4%E3%83%B3%E3%82%B7%E3%83%A5%E3%82%BF%E3%82%A4%E3%83%B3)より
万有引力の原因は、2つの物体が、一般相対性理論によって片方が時空が歪め、その歪みによってもう片方の物体が力を受けるということをアインシュタイン自ら提唱しました。

式にするとニュートンの万有引力の式とは大きく変わり以下のようになるようです(なんかかっこいい)
G_{\mu\nu}=\frac{8\pi G}{c^4}T_{\mu\nu}
$G_{\mu\nu}$はアインシュタインテンソルといって時空の曲がり方を示し、$G$は重力定数、$c$は光速、$T_{\mu\nu}$はテンソルで、エネルギー、運動量テンソルと呼ばれエネルギー・運動量の流れや密度を相対論的に記述した量です。
近接力の招待は時空が歪んだことによる効果であることは上記の式より説明出来ますが、重力波の正体はこの時空の歪みが時間運動した時に波として発生します。
残念ながら、地球-太陽間の重力波も検出可能なはずですが、理論的にとても小さく検出することが大変困難です。
どのくらい小さいのかと言うと、ブラックホール生成時に発生する重力波で太陽と地球の間の距離が、水素原子一個分だけ動いても感知できるレベルと言われています。
重力波観測とLIGOについて
重力波観測機の精度は、「太陽と地球の間の距離が、水素原子一個分だけ動いても感知できるレベルといいましたが、
具体的には、連星ブラックホール合体によって、大きな重力波(とは言っても水素原子一個分だけですが)発生すると予想されていました。
NSF’s LIGO Has Detected Gravitational Waves
レーザー干渉計について
LIGO(Laser Interferometer Gravitational-Wave Observatory:レーザー干渉計重力波観測所)というのは重力波を測定する施設名でライゴと読みます。ここの施設ではじめて重力波が観測されました。
重力波測定の模式図は以下の様になります。

重力波が初めて実証された論文(Phys. Rev. Lett. 116, 061102 (2016))から抜粋
測定された波の重ね合わせから重力波の観測をこころみているのですが、具体的にどの様にしてこの干渉計が動作しているかの説明は以下の通り
https://www.gw.hep.osaka-cu.ac.jp/openworks/whatisgw.html
https://imgur.com/gallery/0VhrXPV
測定した場所について
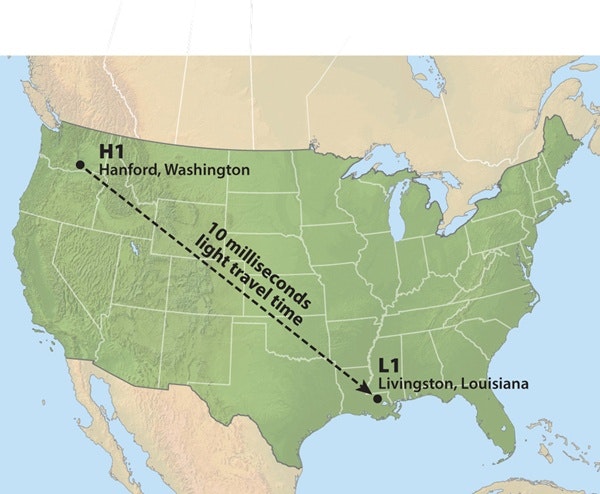
重力波の測定はワシントン州のハンフォードとルイジアナ州のリビングストンの2個所で行なわれていました。
以下H1とかL1という用語が出ますが、H1はハンフォードの観測所による結果で、L1はリビングストンの観測所による結果になります。
2つの観測所で観測することで、偶然発生したものか判断することができます。
予想される結果について
予想される結果は以下の様になります。連星ブラックホールがお互いに近づいて行って、合体するときに最も大きな重力波が発生し、その結果、振幅が最も大きくなります。今回の分析の実戦でこちらの結果を導出するところまでやろうと考えています。
 [Phys. Rev. Lett. 116, 061102 (2016)](https://journals.aps.org/prl/pdf/10.1103/PhysRevLett.116.061102)より
[Phys. Rev. Lett. 116, 061102 (2016)](https://journals.aps.org/prl/pdf/10.1103/PhysRevLett.116.061102)より
重力波とPythonについて
Pythonは主に機械学習や深層学習において現在大流行しておりますが、驚く事にこのOSSの汎用言語が重力波の観測に使われていたのです。
(参考)
Pythonが熱い!データ解析から学ぶPython
[重力波とPythonとIntelと十億年の響き - Blogs@Intel]
(https://news.mynavi.jp/article/20160301-a595/)
PYTHON, EINSTEIN, AND THE DISCOVERY OF GRAVITATIONAL WAVES AT PYCON ITALIA
上記の記事をみると、データ分析だけでなく、システムとしても使用しているらしいので、OSSの言語であるPythonが重力波という高度な学術分野に使われていたことは、大変興味深いことです。
Pythonはわかりやすく、データ分析において高速で動かせるライブラリーなど(sciki-learn,scipy,tensorflowなど)が充実しているため、最近注目されているのも納得な言語だと思います。
それでは、実際に手を動かしながら、Pythonを使ってデータ分析実践をしていきます。
重力波を実際Pythonで解析してみよう
実際には以下のコードを参考にコードを細部は省略しながらポイントを解説してみます。
https://losc.ligo.org/s/events/GW150914/LOSC_Event_tutorial_GW150914.html
自分で書いたわけでなく、コードの解説がメインです。今回の解説では必要ないデータを読み込んでいたりしますが、そこの所は、公式のものと対応付けていただければと思います。
また、Pythonがわからない、これから解析してみたいという方でもわかるような解説を心がけました。スペクトル解析や白色化、マッチドフィルター法など統計的な解析手法がいっぱい詰まっていいトレーニングになります。
パソコンの環境としてPython3.xと、anacondaを入れておくと便利です。(私の手元のPCがMacなので、Macを想定していますがPython3.xのanacondaがセッティングされていれば大丈夫だと思います。)
anacondaをインストールすると以下の全てが入っていると思いますが、観測したrawデータのファイルを読んだり図示したりするパッケージをインストールます(numpy, matplotlib, scipy, h5py, json )
$ pip install numpy
$ pip install matplotlib
$ pip install scipy
$ pip install h5py
$ pip install json
他にも、読み込みにreadligo.pyというpythonのコードと、BBH_events_v3.jsonが必要なので、ダウンロードして、自分の解析したいファイルがあるディレクトリーにおいてください。
readligo.py
https://losc.ligo.org/s/sample_code/readligo.py
BBH_events_v3.json
https://losc.ligo.org/s/events/BBH_events_v3.json
データの取得、生データプロット
まずは、観測所から取得された生データを取得します。
# -- 連星ブラックホールのチュートリアルです。
# -- eventnameは'GW150914' に設定します。GW150914とは重力波のシグナルネームで、はじめて重力波が観測された2015年9月14日という意味です。その他の観測は今回は使いません。
eventname = ''
eventname = 'GW150914'
# eventname = 'GW151226'
# eventname = 'LVT151012'
# eventname = 'GW170104'
# プロットする場合は1
make_plots = 1
plottype = "png"
# plottype = "pdf"
# 解析にスペクトル解析に必要なライブラリーをインポート、詳細はあとで説明
import numpy as np
from scipy import signal
from scipy.interpolate import interp1d
from scipy.signal import butter, filtfilt,iirdesign, zpk2tf, freqz
import h5py
import json
# 描画するためのライブラリーをインポート。jupyter内で出力する場合は%matplotlib inlineとし、retinaは高解像度で表示
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import matplotlib.pyplot as plt
import matplotlib.mlab as mlab
# readligo.py に重力波のデータを読み込む特殊なメソッドがあるので、rlという名前でインポート
import readligo as rl
# もし実行して、matplotlib warning が出ても無視
# Extract the parameters for the desired event:
event = events[eventname]
fn_H1 = event['fn_H1'] # H1(ハンフォード)で観測されたデータ
fn_L1 = event['fn_L1'] # L1(リビングストン)で観測されたデータ
fn_template = event['fn_template'] # 予想されるテンプレートのデータ
fs = event['fs'] # サンプルレート(今回は4096)
tevent = event['tevent'] # 重力波のイベントの起こった時間
fband = event['fband'] # バンドパスシグナルの周波数帯
print("Reading in parameters for event " + event["name"])
print(event)
# ----------------------------------------------------------------
# Load LIGO data from a single file.
# FIRST, define the filenames fn_H1 and fn_L1, above.
# ----------------------------------------------------------------
try:
# read in data from H1 and L1, if available:
strain_H1, time_H1, chan_dict_H1 = rl.loaddata(fn_H1, 'H1')
strain_L1, time_L1, chan_dict_L1 = rl.loaddata(fn_L1, 'L1')
except:
print("Cannot find data files!")
print("You can download them from https://losc.ligo.org/s/events/"+eventname)
print("Quitting.")
quit()
# both H1 and L1 will have the same time vector, so:
time = time_H1
# the time sample interval (uniformly sampled!)
dt = time[1] - time[0]
# Let's look at the data and print out some stuff:
print('time_H1: len, min, mean, max = ', \
len(time_H1), time_H1.min(), time_H1.mean(), time_H1.max() )
print('strain_H1: len, min, mean, max = ', \
len(strain_H1), strain_H1.min(),strain_H1.mean(),strain_H1.max())
print( 'strain_L1: len, min, mean, max = ', \
len(strain_L1), strain_L1.min(),strain_L1.mean(),strain_L1.max())
# What's in chan_dict? (See also https://losc.ligo.org/tutorials/)
bits = chan_dict_H1[b'DATA']
print("For H1, {0} out of {1} seconds contain usable DATA".format(bits.sum(), len(bits)))
bits = chan_dict_L1[b'DATA']
print("For L1, {0} out of {1} seconds contain usable DATA".format(bits.sum(), len(bits)))
# plot +- deltat seconds around the event:
# index into the strain time series for this time interval:
deltat = 5
indxt = np.where((time >= tevent-deltat) & (time < tevent+deltat))
print(tevent)
if make_plots:
plt.figure()
plt.plot(time[indxt]-tevent,strain_H1[indxt],'r',label='H1 strain')
plt.plot(time[indxt]-tevent,strain_L1[indxt],'g',label='L1 strain')
plt.xlabel('time (s) since '+str(tevent))
plt.ylabel('strain')
plt.legend(loc='lower right')
plt.title('Advanced LIGO strain data near '+eventname)
plt.savefig(eventname+'_strain.'+plottype)

ここまでが生データのプロットです。長かったですが、これでやっと解析できます。
H1はハンフォード、L1がリビングストンで観測されたデータになります。
最終的に見たいデーターは先ほど示したのですが、このデータだと、ノイズが大き過ぎてわかりません。
今から、このデータの各周波数ごとのエネルギーや感度を計算したいと思います。
周波数解析について、時間領域のグラフは信号が時間と共にどう変化するかを表すが、周波数領域のグラフは、その信号にどれだけの周波数成分が含まれているかを示しています。wikipedia周波数領域
ノイズの原因も、周波数(または波の周期)を調べることによって解決することができます。
早速やって見ます。
make_psds = 1
if make_psds:
# number of sample for the fast fourier transform:
NFFT = 4*fs
Pxx_H1, freqs = mlab.psd(strain_H1, Fs = fs, NFFT = NFFT)
Pxx_L1, freqs = mlab.psd(strain_L1, Fs = fs, NFFT = NFFT)
# We will use interpolations of the ASDs computed above for whitening:
#白色化のためにパワースペクトル密度(ASDs)のinterpolationsをつかう
psd_H1 = interp1d(freqs, Pxx_H1)
psd_L1 = interp1d(freqs, Pxx_L1)
# Here is an approximate, smoothed PSD for H1 during O1, with no lines. We'll use it later.
# 下の計算はどの様に行なわれているか不明
Pxx = (1.e-22*(18./(0.1+freqs))**2)**2+0.7e-23**2+((freqs/2000.)*4.e-23)**2
psd_smooth = interp1d(freqs, Pxx)
if make_plots:
# plot the ASDs, with the template overlaid:
f_min = 20.
f_max = 2000.
plt.figure(figsize=(10,8))
plt.loglog(freqs, np.sqrt(Pxx_L1),'g',label='L1 strain')
plt.loglog(freqs, np.sqrt(Pxx_H1),'r',label='H1 strain')
plt.loglog(freqs, np.sqrt(Pxx),'k',label='H1 strain, O1 smooth model')
plt.axis([f_min, f_max, 1e-24, 1e-19])
plt.grid('on')
plt.ylabel('ASD (strain/rtHz)')
plt.xlabel('Freq (Hz)')
plt.legend(loc='upper center')
plt.title('Advanced LIGO strain data near '+eventname)
plt.savefig(eventname+'_ASDs.'+plottype)

パワースペクトルの平方根が感度を示す振幅スペクトル密度というものですが、Pythonでは、matplotlibの中にあるmatplotlib.psdを用いて簡単に解析できます。interp1dはinterpolation(内挿、補間法)のことで、"数学で、関数において、二つ以上の点での関数値が知られているとき、その間の任意の点に対する関数値あるいは近似値を求める方法です"(詳しくは内挿、補間法について又は、scipy.interpolate.interp1dの公式のドキュメント参照)
白色化(Whitening)
白色化の目的はデータの成分間の相関を無くすことです。
上記のデータにより、100~300hzでFlatで(相関がない)、他の領域は相関した関係があるので、その領域の相関を無くせば、見たい領域のシグナルをよりシャープに見ることができます。画像解析などの前処理でよく使うそうですが、白色化のイメージは以下が参考になりました。
上記のASDから、80〜300Hzでは平坦ですがそれ以外の領域では周波数とともに感度が大きくなってしまいます(相関がある)。 これを白色化することで、余分なノイズを抑えて、最も感度の高い帯域の弱い信号をキレイに見ることができます。
具体的にやっている作業は以下の通りです
"ここでの白色化の操作は、観測データをフーリエ変換して各周波数の成分(複素数)を求め、その絶対値で割り算し、フーリエ逆変換で元に戻すという方法です。これにより、観測データ全体に入っているような周波数ほど抑えられ、局地的にしか入っていないデータが強調されることになります。"
(Mathematicaで重力波データを解析から抜粋)
以下に白色化についてのコードを示します。
# function to whiten data
def whiten(strain, interp_psd, dt):
Nt = len(strain)
freqs = np.fft.rfftfreq(Nt, dt)
#freqs1 = np.linspace(0,2048.,Nt/2+1)
# whitening: transform to freq domain, divide by asd, then transform back,
# taking care to get normalization right.
#ホワイトニング:周波数領域に変換し、asdで割った後、正規化が正しく行われるように気をつける
hf = np.fft.rfft(strain)
norm = 1./np.sqrt(1./(dt*2))
white_hf = hf / np.sqrt(interp_psd(freqs)) * norm
white_ht = np.fft.irfft(white_hf, n=Nt)
return white_ht
whiten_data = 1
if whiten_data:
# now whiten the data from H1 and L1, and the template (use H1 PSD):
strain_H1_whiten = whiten(strain_H1,psd_H1,dt)
strain_L1_whiten = whiten(strain_L1,psd_L1,dt)
#バンドパスフィルタによる高周波ノイズを除去
bb, ab = butter(4, [fband[0]*2./fs, fband[1]*2./fs], btype='band')
normalization = np.sqrt((fband[1]-fband[0])/(fs/2))
strain_H1_whitenbp = filtfilt(bb, ab, strain_H1_whiten) / normalization
strain_L1_whitenbp = filtfilt(bb, ab, strain_L1_whiten) / normalization
以上により白色化された結果が得られました。
重力波可視化
白色化によって得られたデータを出力してみます。
# ここのコードについては個人の解釈を元に色々変えました。
strain_whitenbp = strain_L1_whitenbp
plt.figure(figsize=(15,12))
plt.subplot(2,1,1)
plt.plot(time-tevent,strain_whitenbp,"b",label='L1 whitened h(t)')
# 上下の反転しているためひっくり返します
# L1とH1の観測場所の違いから7ms全体をずらす
strain_whitenbp = -strain_H1_whitenbp
t_test=time-tevent-0.007
plt.plot(t_test,strain_whitenbp,"r",label=' H1whitened h(t)')
# plt.plot(time-tevent,template_match,'k',label='Template(t)')
plt.ylim([-10,10])
plt.xlim([-0.15,0.05])
plt.grid('on')
plt.xlabel('Time (s)')
plt.ylabel('whitened strain (units of noise stdev)')
plt.legend(loc='upper left')
plt.show()

L1(リビングストン)とH1(ハンフォード))の観測地点の違いから7msズレていたので、それを考慮にいれて、振幅は反転しても本質的に違いは無いのでH1の振幅に全体にマイナスをかけることでひっくり返しました。
上記のデータにより見事に論文図示されているものと同じ結果になりました。
最期にこのシグナルが重力波であるかどうかの検証をします。
そのためにマッチドフィルター法と言う方法を用いて解析します。
マッチドフィルター法について
マッチドフィルター法とは理論的に予測された波形をテンプレートにし、実験データとの相関を計算するという探索手法です。
LIGOの計算では用いられておりませんでしたが、scipy.signal.correlateで計算できるみたいです(直感的でわかりやすい)

図はscipyの公式ドキュメントのscipy.signal.correlateより
残念ながら計算が結構大変なので(理解できなかったわけではない(笑))、結果だけ掲載致しますが、マッチドフィルターを用いた数値計算との比較は以下の様になり、今回の結果が連星ブラックホールによる重力波であると理論的な観点からも証明することができました。

今回の重力波で具体的に計算されたマッチドフィルターによる詳細は
An algorithm for detection of gravitational waves from inspiraling compact binaries B. Allen et al., PHYSICAL REVIEW D 85, 122006 (2012)
のsection IVに詳しく記載されています。
以上でPythonによる数値計算の結果でした。
もちろん、このような単純な分析でだけでなく、様々な紆余曲折があったはずですが、この世紀の大発見の裏で、Pythonや統計学などが寄与していたことは間違いなさそうです。
公式のノートブックでは上記の計算以外にも色々と計算していて、"重力波を聞いいてみる"という興味深い項目もありましたので、興味のある人は是非Pythonで色々動かしてみて(Jupyterはほんと便利)データ分析してみてください。
重力波でわかること
最期に重力波で何がわかる様になるのか簡単に説明したいと思います。
重力波は透過性が良い
従来の電磁波による観測方法では、重力波が発生するイベント(ブラックホール連星、中性子星連星、超新星爆発)がどこで発生しているのか断定することが出来ませんでした。今回の発生よりどこで重量波が発生しているのか方向がわかります。先ほどのL1とH1の発生したそれぞれの波形のずれから、どの方向から重力波がきたのか特定することができます。
それによって特定された方向から、従来の電磁波による測定と合わせて、より正確な宇宙のできごとを探ることが出来ます。
(いい感じの模式図が無かったので、図は後ほど掲載予定)
物質が生まれた起源や、宇宙の起源がわかるかも
詳細な計算はすっ飛ばして解説しましたが、今回の重量波の結果を解析した結果、太陽の36倍と29倍のブラックホールの合体によるものということがわかりました。従来の考えでは太陽の10倍ほどの質量程度と見積もられていたものが大きく見直されました。これほど大きくなったきっかけに、重い元素(金やプラチナ)が中性子連星の衝突によって起るのではないかと考えられるようになりました。従来までわからなかった重い元素の起源を探ることができる可能性が示唆されました。また、宇宙の始まった時に発生した急激な膨張(インフレーション)の際にも非常に大きな重力波が発生していたと言われています。この重力波から宇宙の起源も知ることができるのではないかと期待されています。
まだまだ様々な知見や面白いトピックがありますので、さらに知りたい方は是非私が参考にしたブルーバックスや、その他の解説書を読んで見てください。
最後に
いかがだったでしょうか。これでもむずかしかったと思いますが、雰囲気が分かって貰えば幸いです。
私自身、宇宙物理はもちろんのこと、マッチドフィルターや信号処理についてもまだまだ、わからないことだらけなので、もっといい記事を書けるよう精進してまいります。
※2017年8月に中性子星連星のも発見された様ですが、今回は特に触れませんでした。中性子連星の分析も後日やって見たいものです。
※載せて無かった図やコードについての解説も追加でもう少しする予定です。
また、質問、訂正についても大歓迎です。どうぞよろしくお願いいたします。