はじめに
これは、二分探索木の一つである赤黒木についての記事です。
この記事中の図は以下を用いて作成しました。
visualization
関連記事:
参考:
これで分かった赤黒木
赤黒木とは
ノードを赤と黒で塗り分け、赤と黒の個数や位置関係に関するルールを守ることで平衡を保ちます。
ルールは以下です。
- ノードは赤か黒である
- 根は黒である
- 赤いノードの子は黒である
- 葉から根のパス上に存在する黒の個数は、全てのパスで同じである
上記ルールにより、黒は連続しますが、赤は連続しません。
考えうる最短のパスは黒が連続し、最長のパスは赤と黒が交互に登場します。
最短と最長でも黒の数は同じなので、最長のパスは最短のパスの2倍に収まります。
操作
検索
赤黒木は二分探索木であるため、「左の子<=親<=右の子」というルールが使えます。
二分探索木と同じ実装で十分です。
追加
赤黒木では、追加するノードは「赤」です。
よって、赤の子としてノードを追加する場合に注意が必要です。
根に追加する場合、追加したノードの色を黒に変更して追加操作は完了します。
黒の子として追加する場合、赤黒木のルールを満たすので、これ以上の操作は不要です。
赤の子として追加する場合、追加した後に変形が必要です。
これは以下の2パターンの形があります。(実際には左右反転した形もあるので4パターンです)

一直線(図の左)の場合、一番上のノードについて右回転し、真ん中を赤、それ以外を黒とすれば完了します。
ねじれ(図の右)の場合、真ん中のノードについて左回転し、一番上のノードについて右回転し、真ん中を赤、それ以外を黒とすれば完了します。
回転操作のあと、根が赤になっていたら根を黒にします。
根を常に黒くするのを追加操作の一番最後に実施したく、黒くする操作をaddに、addから再帰処理をするaddAndBalanceを呼び出すようにしました。
public RBNode add(RBNode node, int value) {
node = addAndBalance(node, value);
node.color = Color.BLACK;
return node;
}
private RBNode addAndBalance(RBNode node, int value) {
if (node == null) {
return new RBNode(value);
}
if (node.value == value) {
return node; // 重複を許さない実装のため何もしない
}
if (node.value > value) {
node.left = addAndBalance(node.left, value);
} else {
node.right = addAndBalance(node.right, value);
}
return balance(node);
}
private RBNode balance(RBNode node) {
if (node.color == Color.RED) {
return node;
}
if (node.left != null && node.left.color == Color.RED) {
if (node.left.left != null && node.left.left.color == Color.RED) {
node = rotateRight(node);
node.color = Color.RED;
node.left.color = Color.BLACK;
node.right.color = Color.BLACK;
} else if (node.left.right != null && node.left.right.color == Color.RED) {
node.left = rotateLeft(node.left);
node = rotateRight(node);
node.color = Color.RED;
node.left.color = Color.BLACK;
node.right.color = Color.BLACK;
}
}
if (node.right != null && node.right.color == Color.RED) {
if (node.right.right != null && node.right.right.color == Color.RED) {
node = rotateLeft(node);
node.color = Color.RED;
node.left.color = Color.BLACK;
node.right.color = Color.BLACK;
} else if (node.right.left != null && node.right.left.color == Color.RED) {
node.right = rotateRight(node.right);
node = rotateLeft(node);
node.color = Color.RED;
node.left.color = Color.BLACK;
node.right.color = Color.BLACK;
}
}
return node;
}
private RBNode rotateLeft(RBNode node) {
RBNode r = node.right;
RBNode rl = r.left;
node.right = rl;
r.left = node;
return r;
}
private RBNode rotateRight(RBNode node) {
RBNode l = node.left;
RBNode lr = l.right;
node.left = lr;
l.right = node;
return l;
}
public static void main(String[] args) {
RBNode root = add(null, 5);
root = add(root, 3);
root = add(root, 7);
root = add(root, 1);
/**
└── 3(BLACK)
├── L:1(BLACK)
└── R:5(BLACK)
└── R:7(RED)
*/
root = add(root, 6);
/**
└── 3(BLACK)
├── L:1(BLACK)
└── R:6(RED)
├── L:5(BLACK)
└── R:7(BLACK)
*/
}
※一般的には回転をおこなわずに色だけ変えるパターンを加えて3パターン(左右合わせて6パターン)とすることが多いようです。
参考にさせていただいたサイト:これで分かった赤黒木によると、効率性を重視すると6パターンになるのだろうとのことです。
効率性の話でいうと上記のコードはそれ以外にも工夫するべき点があります(終了条件を設けず、最後までbalanceを実行してますが、もっと回数を削減できるはず)ので、理解を優先して2パターン(左右で4パターン)のやり方で実装しています。
削除
AVL木が満たすべきルールは「高さ」だったので、追加でも削除でも高さが変われば調整すればOKでした。そのため、追加時と削除時に呼ぶbalanceは同じ内容で良かったのです。
対して、赤黒木はそれぞれのノードを色分けしているため、追加と削除では全く調整ロジックが異なります。
削除では、黒を消す場合に注意が必要です。
黒を消した場合、そのノードを通るパスの黒の個数が1減りますので、バランスをとる必要があるということです。
赤を消しても赤黒木のルールには何ら影響を及ぼしませんので、通常の二分探索木の削除ロジックを実行して終わりです。
黒を消した場合、そのノードを通るパスの黒の個数が減るので、「親を黒くしてパスの黒を増やす」か「他のパスの黒を移動させる」必要があります。
まず以下のように、兄弟が黒で赤の子を持つ場合を考えます。

「?」を黒にして左に持ってこれれば、左の黒ノードを消した分黒を増やすことができます。
「?」を左に持ってくるには回転を行えば良いですね。
図の左の場合は「?」に対する左回転、図の右の場合は「?」の子(削除対象の兄弟)に対して右回転ののち「?」に対して左回転で実現できます。
この操作をして兄弟側に影響がないのかを考えましょう。
元々兄弟の子(黒の子)であった部分木は、黒になった「?」の下に移動するので、パス上の黒の個数は変わりません。元々兄弟の孫(赤の子)であった部分木は、兄弟が根の位置に移動し、その子である赤の子として引き続き紐づくので、こちらもパス上の黒の個数は変わりません。
よって、兄弟側の黒の個数を変えずに、削除したパスの黒のみを増やせていることがわかります。
続いて、兄弟が黒で赤の子を持たない場合を考えます。

先ほどと違って、回転によって左側に黒を移動すると、右の黒が減ってしまいます。
そこで、親である「?」を黒にしてみます。すると、左側は思った通りに黒が1つ増えますが、右の黒も増えてしまいました。そこで、兄弟を赤くすると、右の黒の個数を変えずに、左の黒の個数を増やせることがわかります。
ただし、ここで問題のなのは「?」が元々黒かった場合です。
黒を増やすために「?」を黒にしていますから、元が黒なら黒を増やすことができません。
このように、「黒を黒にする必要がある」状態を「二重黒」と呼びます。
二重黒が発生した場合は、そのノードが二重黒であることを保持しておき、その親の位置で修正します。
最後に、兄弟が赤の場合です。
赤は連続しないため、親は黒であることが確定します。
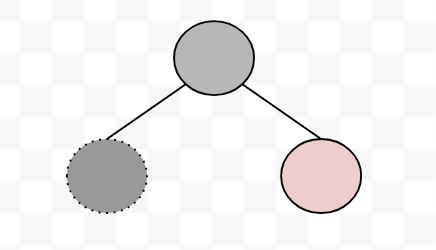
親に対して左回転をかけた場合を考えると、左の黒の個数は+1、右の黒の個数は−1されることがわかります。
そこで、回転後、元々親だったノードを赤(黒から赤に変更)、元々兄弟だったノードを黒(赤から黒に変更)すると、左の黒の個数+1、右の黒の個数は変動なし、とできます。
以上が削除時のバランスの取り方です。
二分探索木の同じロジックで削除を実行した後、上記のロジックでバランスをとりましょう。
public RBNode delete(RBNode node, int target) {
node = deleteAndFix(node, target);
node.color = Color.BLACK;
node.doubleBlack = false;
return node;
}
public RBNode deleteAndFix(RBNode node, int target) {
if (node == null) {
return null;
}
if (node.value == target) {
if (node.right == null && node.left == null) {
if (node.color == Color.BLACK) {
// 黒を消したことを親に伝えるために値が0のノードとして残す
node.value = 0;
return node;
}
return null;
}
if (node.left == null) {
if (node.color == Color.BLACK) {
node.right.changeBlack();
}
return node.right;
}
if (node.right == null) {
if (node.color == Color.BLACK) {
node.left.changeBlack();
}
return node.left;
}
int min = getMin(node.right);
node.value = min;
node.right = deleteAndFix(node.right, min);
} else if (node.value > target) {
node.left = deleteAndFix(node.left, target);
} else {
node.right = deleteAndFix(node.right, target);
}
return fix(node);
}
private int getMin(RBNode node) {
if (node.left == null) {
return node.value;
}
return getMin(node.left);
}
private RBNode fix(RBNode node) {
if (!node.needFix()) {
return node;
}
if (node.left != null && (node.left.value <= 0 || node.left.doubleBlack)) {
// 0のノード、もしくは二重黒があれば修正する
node.left.doubleBlack = false;
if (node.left.value == 0) {
node.left = null;
}
if (getColor(node.right) == Color.BLACK) {
if (node.right == null) {
node.changeBlack();
} else if (getColor(node.right.right) == Color.RED) {
node = rotateLeft(node);
} else if (getColor(node.right.left) == Color.RED) {
node.right = rotateRight(node.right);
node = rotateLeft(node);
} else {
node.right.color = Color.RED;
node.changeBlack();
}
} else {
node = rotateLeft(node);
}
return node;
}
// 0のノード、もしくは二重黒があれば修正する
if (getColor(node.left) == Color.BLACK) {
node.right.doubleBlack = false;
if (node.right.value == 0) {
node.right = null;
}
if (node.left == null) {
node.changeBlack();
} else if (getColor(node.left.left) == Color.RED) {
node = rotateRight(node);
} else if (getColor(node.left.right) == Color.RED) {
node.left = rotateLeft(node.left);
node = rotateRight(node);
} else {
node.left.color = Color.RED;
node.changeBlack();
}
} else {
node = rotateRight(node);
}
return node;
}
private Color getColor(RBNode n) {
return (n == null) ? Color.BLACK : n.color;
}
public class RBNode {
public boolean needFix() {
if (left == null && right == null) {
return false;
}
return left != null && (left.value <= 0 || left.doubleBlack)
|| right != null && (right.value <= 0 || right.doubleBlack);
}
public void changeBlack() {
doubleBlack = color == Color.BLACK; // 元々黒なら二重黒とする
color = Color.BLACK;
}
}
public static void main(String[] args) {
RBNode root = add(null, 5);
root = rbt.add(root, 3);
root = rbt.add(root, 7);
root = rbt.add(root, 1);
root = rbt.add(root, 6);
root = rbt.add(root, 8);
p.printWithColor(root, "", false, "");
/**
└── 3(BLACK)
├── L:1(BLACK)
└── R:6(RED)
├── L:5(BLACK)
└── R:7(BLACK)
└── R:8(RED)
*/
root = rbt.delete(root, 6);
p.printWithColor(root, "", false, "");
/**
└── 3(BLACK)
├── L:1(BLACK)
└── R:7(RED)
├── L:5(BLACK)
└── R:8(BLACK)
*/
root = rbt.delete(root, 7);
p.printWithColor(root, "", false, "");
/**
└── 3(BLACK)
├── L:1(BLACK)
└── R:8(BLACK)
├── L:5(RED)
*/
}
おわりに
AVL木と比べて難しすぎる〜と思いました。実装するにはお絵描き必須ですね。ぜひノートとペンを用意して望んでください。
deleteがなかなか理解できなくて、一度諦めたのですが、B木を実装してみた後だと割とすんなり理解できました。お困りの方はぜひB木の実装にもチャレンジしてみてください。
ところで、難しさの割に、AVL木の方がパフォーマンスは優れているそうです。
じゃあどこで使うんだ、と思ったのですが、JavaのTreeMapの実装は赤黒木でした。結構身近なところで使われているんですね。