はじめに
これは、二分探索木の一つであるAVL木についての記事です。
この記事中の図は以下を用いて作成しました。
visualization
木構造の全般的な説明はこちら
二分探索木についてはこちら
※実装は二分探索木を元に書いていますので、適宜参照しつつ読み進めてください。
参考:
これで分かったAVL木
AVL木とは
各ノードの左部分木と右部分木の高さの差を1以下することで平衡を保つ二分探索木です。
ノードを追加した結果上記を満たさなくなった場合、「回転」という操作をすることで上記を満たす形に木構造を変更します。
操作
最初の状態を以下とします。
これはAVL木の定義を満たします。

検索
AVL木は二分探索木であるため、「左の子<=親<=右の子」というルールが使えます。
二分探索木と同じ実装で十分です。
追加
大きく分けて二つのフェーズがあります。
挿入フェーズ
二分探索木のルール(左の子<=親<=右の子)を満たすような位置にノードを追加します。
次のフェーズと組み合わせることで少し変わりますが、一旦、二分探索木と同じ実装と理解してください。
バランスをとるフェーズ
まずはAVL木のルール(左部分木と右部分木の高さの差が1以下)を満たしているかを確認します。
AVL木のルールを満たしていない場合、ルールを満たすように木構造を変形します。
二分探索木のルールを満たしたまま変形する操作を「回転」と呼びます。
例えば、1,2のノードがあり、3を挿入した場合、挿入フェーズが完了すると以下の状態になります。
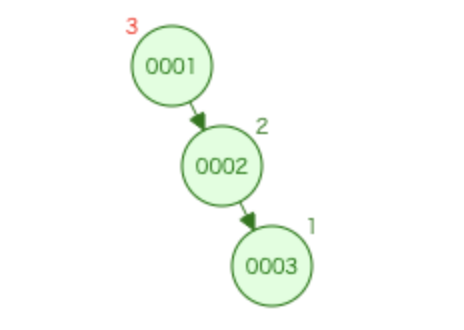
根(1のノード)を見ると、左部分木の高さが0, 右部分木の高さが2のため、AVL木のルールを満たしません。
右部分木が高いので、何とかして左に移動させたいです。
根の値は1で、3つのノードの最小値です。最小値が根だと、それ以外のノードは右の子として存在することになります。つまり、根は1のままではいけないとわかります。
そこで、根を2とすることを考えると、以下の形にできます。
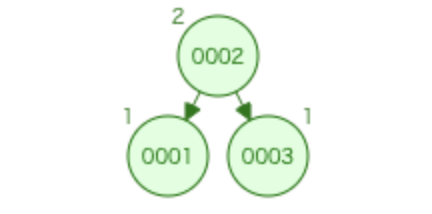
これで、左部分木と右部分木の高さが1, その差分を0にできました。
1を持って、くるっと左回りに回すようなイメージなので、この操作は「左回転」と呼ばれます。
この時行った操作を(回転のアルゴリズムに準えて)整理すると以下になります。
- 2の左の子(空)を1の右の子にする
- 1を2の左の子にする
右部分木が高い場合は左回転を、左部分木が高い場合は右回転をすると、AVL木のルールを満たすように変形ができます。
また、「ねじれ」のパターンも考えましょう。
今度は、1,3のノードがあり、2を追加することを考えます。挿入フェーズが完了すると以下の状態になります。

先ほどと同じく、登場する値は「1,2,3」の3つですから、根を2にしたいところです。
つまり、先ほどの挿入フェーズ完了時点の形にできれば、あとは左回転をして平衡にできるというわけです。
先ほどの挿入フェーズ完了時点の形と見比べると、3と2のノードを逆転できれば良さそうですね。
これは、3を持ってくるっと右回りに回すイメージです。3のノードに対して右回転をかければ先ほどの挿入フェーズ完了時点の形にできます。
よって、右部分木が高く「ねじれ」のある場合は、あるノードの右の子に対して右回転をかけたのち、ノードに対して左回転をかければ良いということになります。
左部分が高く「ねじれ」のある場合はその反対です。あるノードの左の子に対して左回転をかけたのち、ノードに対して右回転をかければ良いということです。
実装
二分探索木の実装におけるaddの最後にbalanceを呼ぶようにしています。
public Node add(Node node, Node newNode){
if(node == null) {
return newNode;
}
if(node.value == newNode.value) {
// 重複を許さないので何もしない
return node;
}
if(node.value > newNode.value) {
node.left = add(node.left, newNode);
}
else {
node.right = add(node.right, newNode);
}
node = balance(node);
return node;
}
private Node balance(Node node) {
updateHeight(node);
int bias = getBias(node);
if(-1 <= bias && bias <= 1) {
return node; // AVL木のルールを満たすので何もしない
}
if(bias > 1) {
// 左部分木が高い
if(getBias(node.left) < -1) {
// 左部分木の右が高い=ねじれ
// 左の子に左回転をかける
node.left = rotateLeft(node.left);
}
// 右回転をかける
node = rotateRight(node);
}
if(bias < -1) {
// 右部分木が高い
if(getBias(node.right) > 1) {
// 右部分木の左が高い=ねじれ
// 右の子に右回転をかける
node.right = rotateRight(node.right);
}
// 左回転をかける
node = rotateLeft(node);
}
return node;
}
private void updateHeight(Node node) {
if(node == null) {
return;
}
node.height = Math.max(getHeight(node.left), getHeight(node.right)) + 1;
}
private int getHeight(Node node) {
if(node == null) {
return 0;
}
return node.height;
}
private int getBias(Node node) {
if(node == null) {
return 0;
}
return getHeight(node.left) - getHeight(node.right);
}
private Node rotateLeft(Node node) {
Node r = node.right;
Node rl = r.left;
node.right = rl;
r.left = node;
updateHeight(rl);
updateHeight(node);
updateHeight(r);
return r;
}
private Node rotateRight(Node node) {
Node l = node.left;
Node lr = l.right;
node.left = lr;
l.right = node;
updateHeight(lr);
updateHeight(node);
updateHeight(l);
return l;
}
public static void main(String[] args){
Node root = new Node(5);
root = add(root, new Node(3));
root = add(root, new Node(7));
root = add(root, new Node(1));
root = add(root, new Node(6));
root = add(root, new Node(8));
root = add(root, new Node(9));
root = add(root, new Node(9));
printWithHeight(root, "", false, "");
/**
└── 5(4)
├── L:3(2)
│ ├── L:1(1)
└── R:7(3)
├── L:6(1)
└── R:8(2)
└── R:9(1)
*/
root = add(root, new Node(10));
printWithHeight(root, "", false, "");
/**
└── 5(4)
├── L:3(2)
│ ├── L:1(1)
└── R:7(3)
├── L:6(1)
└── R:9(2)
├── L:8(1)
└── R:10(1)
*/
}
削除
削除も追加と同じく二つのフェーズに分けて考えましょう。削除フェーズとバランスをとるフェーズです。
削除フェーズは二分探索木と同じ、バランスをとるフェーズは上述した追加の場合と同じです。
public Node delete(Node node, int target) {
if(node == null) {
return node;
}
if(node.value == target) {
if(node.left == null && node.right == null) {
node = null;
}
else if(node.left == null) {
node = node.right;
}
else if(node.right == null) {
node = node.left;
}
else {
int min = getMin(node.right);
node.right = delete(node.right, min);
node.value = min;
}
}
else if(node.value > target) {
node.left = delete(node.left, target);
} else{
node.right = delete(node.right, target);
}
node = balance(node);
return node;
}
public static void main(String[] args){
Node root = new Node(5);
root = add(root, new Node(3));
root = add(root, new Node(7));
root = add(root, new Node(1));
root = add(root, new Node(6));
root = add(root, new Node(8));
root = add(root, new Node(9));
root = add(root, new Node(9));
root = add(root, new Node(10));
printWithHeight(root, "", false, "");
/**
└── 5(4)
├── L:3(2)
│ ├── L:1(1)
└── R:7(3)
├── L:6(1)
└── R:9(2)
├── L:8(1)
└── R:10(1)
*/
root = delete(root, 1);
printWithHeight(root, "", false, "");
/**
└── 7(3)
├── L:5(2)
│ ├── L:3(1)
│ └── R:6(1)
└── R:9(2)
├── L:8(1)
└── R:10(1)
*/
}
おわりに
回転操作って難しいようで実装を見れば分かるとおり子を付け替えているだけです。とっても単純ですね。でもこれってどうやって思いつくのかがわからなくて、どう説明したものか頭を悩ませました。
コードが簡単な分、アルゴリズムを理解してからじゃないと読めない実装だなーと思ってます。
なお、今回は理解を優先して「挿入フェーズ」「バランスをとるフェーズ」と分けた都合上、効率の悪い実装になっています(やらなくていいタイミングでbalanceをやってる場合がある)。もうバランスが取れていると言えるタイミング(終了条件)とそれを考慮した効率の良い実装は別途お調べください。