オミータです。ツイッターで人工知能のことや他媒体の記事など を紹介していますので、人工知能のことをもっと知りたい方などは @omiita_atiimoをご覧ください!
他にも次のような記事を書いていますので興味があればぜひ!
ラベルへのオーギュメンテーション新登場!「SLA」を解説!
画像データに対するデータオーギュメンテーション(以下、DA)は今では必要不可欠な技術となっており、これまでたくさんのDAが考案されてきています(参考:DAまとめ記事)。ただこれまでのDAは画像自体に適用するものが主流で、ラベルは変更しないというものが多かったです(MixupやCutMixなどソフトラベルを使う例もありますが。)。そこでラベルも変更してしまおう、というのがICML2020で登場した["Self-supervised Label Augmentation via Input Transformations", Lee, H., Hwang, S., Shin, J., (ICML'20)]になります。本記事では、論文で提案されている「SLA」(=Self-supervised Label Augmentation)という手法について解説していきます。「ラベルも変えちゃおうよ」という発想を単純な仕組みで実現しており、画像分類やFew-shotなどで性能向上を果たしています。SLAを早速見ていきましょう。
"Self-supervised Label Augmentation via Input Transformations", Lee, H., Hwang, S., Shin, J., (ICML'20)
公式実装: PyTorch
本記事の流れ:
- 忙しい方へ
-
SLAの解説
- 自己教師あり学習
- SLA
- SLAの実験結果
- まとめと所感
- 参考
| 略称 | 名称 |
|---|---|
| SLA | Self-supervised Label Augmentation |
| DA | Data Augmentation |
| SSL | Self-Supervised Learning |
| AG | Aggregation |
| SD | Self-Distillation |
| SI | Single Inference |
0. 忙しい方へ
- SLAの構成要素は次の3つだよ
- 結合ラベル:「元のラベル」と「適用したDA」の組み合わせを新たなラベルとしたよ
- アンサンブル:予測ラベルは「元の画像」と「DA適用後の画像たち」を全て考慮して出力するよ
- 自己蒸留:推論時にもアンサンブルの効果が得られるように、アンサンブルによる出力を模倣するような線形変換を用意するよ
- CIFAR10/100/TinyImageNetなど幅広いデータセットで大きなゲインを得ているよ
- Few-shotや不均衡データに対しても性能向上を示したよ
1. SLAの解説
SLAは、Self-Supervised Learning(=SSL)にインスピレーションを得ています。ラベル予測にはアンサンブルを用いており、また推論時のスピードを速くするために自己蒸留を用いています。SLAの説明は次の順番で行います。
- Self-Supervised Learning(=SSL)
- Self-supervised Label Augmentation(=SLA)
2.1 結合ラベル
2.2 アンサンブル
2.3 自己蒸留
1.1 Self-Supervised Learning

そもそも教師あり学習の「教師」とは何でしょうか。この教師とはつまり「ラベル」のことでしたね。教師あり学習では、そのラベルを用いてモデルを学習させます。それではSelf-Supervised Learning(=SSL)、自己教師あり学習の「自己教師」とは何のことを指しているのでしょうか。自己教師とは「自ら生成したラベル」のことを指しています。例えば、ある画像を90度回転させた場合にSSLで用いるラベルは「90度」です。このように、画像にDAを適用させてその適用したDAを当てさせるというタスクがSSLにはよくあります(Ex.回転角度)。教師あり学習を行う前の事前学習としてSSLを用いると最終的により高い性能のモデルが出来上がったりします。もっと詳しく知りたい方はこちらのページでSSLについてまとめられていますのでご覧ください。
ただし、論文著者はSSLの問題点として次の2つを上げています。まず、SSLでは教師ラベルを予測する識別器と自己教師ラベルを予測する識別器それぞれ用意するため「学習の難しいマルチタスク学習」になっているという欠点があるということです。また、画像にDA適用してもその予測結果は同じでなければならないので、「不要な一貫性モデルに強制」してしまっています。そのため提案手法であるSelf-supervised Label Augmentation(=SLA)ではこの「マルチタスク学習」と「不要な一貫性の制約」を結合ラベルを用いることで解決しています。
1.2 Self-supervised Label Augmentation
ここからはSLAの説明に入ります。前述したとおり、SLAは主に3つの要素で構成されています。それぞれの役割を簡単に記すと、学習時に使用する「結合ラベル(=Joint Label)」、ラベル予測の精度を上げるための「アンサンブル」、推論時のスピードアップのための「自己蒸留」です。結合ラベルがSLAの一番重要な構成要素で、あとの2つはさらにモデルを良くするためのテクニックのようなものです。
1.2.1 結合ラベル
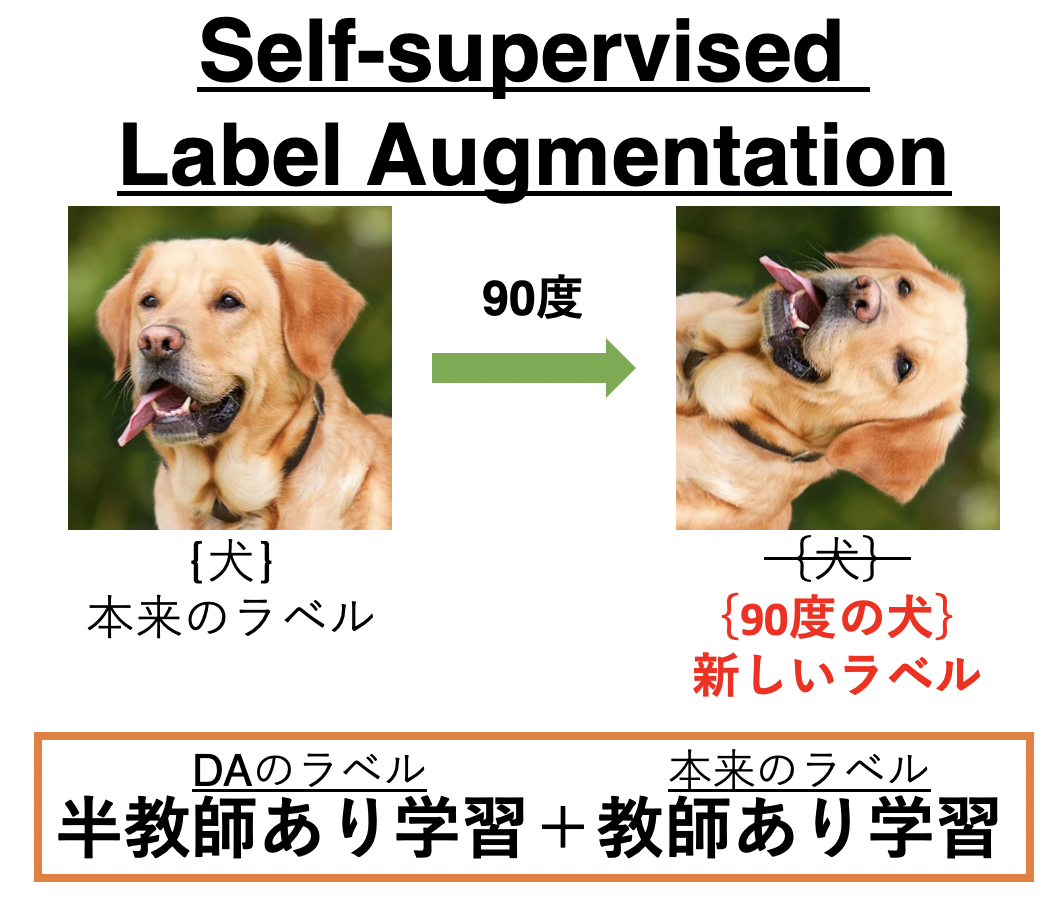
まず、通常学習時に使用するラベルは「犬」や「猫」という画像の意味を示すもの(ここでは便宜上意味ラベルと呼びます。)となります(上図上段)。SSLではこれに加えてDAに対するラベル(回転であれば「0度回転」や「90度回転」など)も用いました(DAラベルとします)。そのため「90度回転」を適用した「犬」の画像であれば、SSLモデルには「90度回転」を予測する識別器と「犬」を予測する識別器が別々でありました(上図中段)。SLAでは、この別々で予測していたものを1つの識別器で一気に予測します。つまり、「90度回転した犬」というラベルとして1つの識別器で予測する、ということです(上図下段)。このように意味ラベルとDAラベルをくっつけたラベルが結合ラベルです。DAラベルが$M$個あり、意味ラベルが$N$個あれば結合ラベルはそれら1つ1つの組み合わせになるので$M\times N$個あるということです。(例えば、DAが回転(0, 90, 180, 270)ならM=4で意味ラベルが犬、猫、馬ならN=3なので、学習に用いる結合ラベルは$4\times3=12$個ということになります。)
結合ラベルは1つの識別器で判断します。またDAが異なる画像なら結合ラベルももちろん異なります。こうして結合ラベルを用いることでマルチタスク学習と一貫性の制約が同時に解決できました。ちなみに、このSLAによって最終層のパラメータ数はわずかに増加しますが全体のネットワークと比べて無視できる程度(ResNet32に対して0.4%の増加)なので問題ありません。ここまでを踏まえて、SLAに対する損失関数は次のように書けます。単純ですね。
\mathcal{L}_\mathrm{SLA}(x, y;\theta, w) = \frac{1}{M}\sum_{j=1}^M\mathcal{L}_\mathrm{CE}(\rho(\tilde{z}_j);w), (y, j))
ここで $x, y, M, \rho(\cdot), \tilde{z}_j$は、それぞれ入力画像、意味ラベル、DAの数、Softmax識別器、DAの$j$を適用した画像$x$の潜在表現を表しています。$\tilde{z}_j$はつまり、DAとニューラルネットをそれぞれ$t(\cdot),f(\cdot)$とすると$\tilde{z}_j=f(t_j(x))$のことです。$\mathcal{L}_\mathrm{CE}$はクロスエントロピーです。ちなみに、学習時は、$M$個のDAが適用された画像たち($M$個)は同時に処理されます。つまり通常の画像が入ってきたらそれに対して$M$個のDAを適用し$M$個の画像を獲得してから実際のニューラルネットへと全て入力する、ということです。ミニバッチ$B$を用いるとSLAによる学習は単に$\frac{1}{|B|}\sum_{(x,y)\in B}\mathcal{L}_\mathrm{SLA}(x,y;\theta,w)$を最小化することになります。ちなみに論文中で取り扱われているDAは回転($M=4$)とRGB入れ替え($M=3!=6$)の2つです(下図例)。
1.2.2 アンサンブル
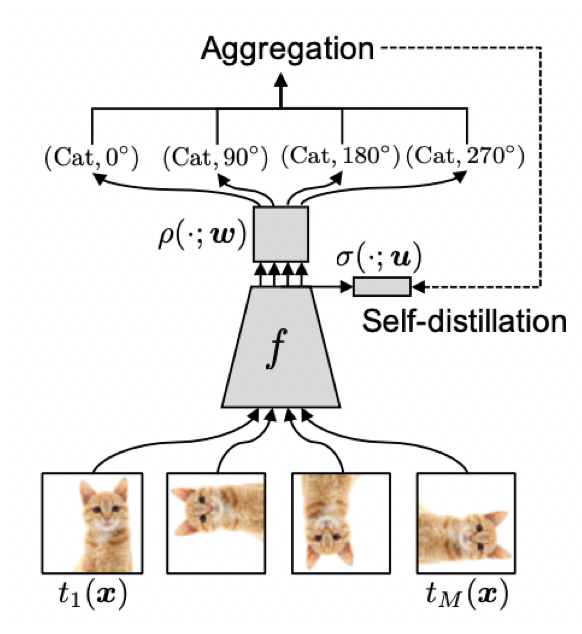
結合ラベルによってSSLの問題点をうまく解決できることはわかりました。ただし、このままではモデルはもちろん結合ラベルを出力してしまいます。予測時の出力は意味ラベルであって欲しいはずです。画像のラベル予測においては、90度猫も270度猫もいずれも「猫」とだけ答えて欲しいです。そこで、実装では、まず角度0度の画像を入力します。この時logitの角度0度の部分だけを抜き取ります(長さ$N$のベクトル)。続いて角度90度にした画像を入力しlogitの角度90度の部分だけを抜き取ります(長さ$N$のベクトル)。角度180度と270度に対しても同様の処理を行います。最終的にそれぞれの角度におけるlogit(のような)ベクトルがあるので、それらを要素ごとに平均して最終的にその平均ベクトル(もちろん長さ$N$のベクトル)に対してSoftmaxをかけて意味ラベルを手に入れます(実際には各角度の画像は順に入れるのではなくミニバッチで一気に入力します)。この処理は、意味ラベルに対する各角度によるアンサンブルと見なすこともできます。論文中ではこのアンサンブル部分をAggregated Inferenceと呼んでいます。

このアンサンブルを式で表すと、
P_\mathrm{aggregated}(i|x)=\frac{\exp(s_i)}{\sum_{k=1}^N\exp(s_k)}
ただし、
s_i = \frac{1}{M}\sum_{j=1}^Mw^\intercal_{ij} \tilde{z}_j
そして最後にPyTorchによる実装例(論文に記載)を示します。AGがアンサンブルによる出力(BxN)を表しています。modelによる出力は4B x 4Nのlogitです。
この推論方法によって、モデルを別々に用意する通常のアンサンブルと同程度の性能を叩き出したというので驚きです。
1.2.3 自己蒸留
先ほどのアンサンブルによって性能は大きく向上するのですが、推論時間がM倍長くなってしまうという欠点があります。それもそのはずで、1枚の予測をするためにまずM個の画像を生成させてそれぞれに対する予測から最終的な予測を1つにするためです。ただし、この推論時間を削減したいです。そのために用いるのが「蒸留」というテクニックです。
ここで用いる蒸留は端的に言えば、「アンサンブルによる出力を模倣させる」というものです。自分自身を模倣しているので自己蒸留です。式で見るともっとわかりやすいかもしれません。自己蒸留というのは次式のKLダイバージェンスを最小化させるような小さなネットワーク$\sigma(z;u)$を用意することになります。ここで$z$はオリジナル画像の埋め込み表現です。
D_{KL}(P_{\mathrm{aggregated}}(\cdot|x)||\sigma(z;u))
この$\sigma(z;u)$はアンサンブルの出力を模倣しているので、推論時はこのネットワークを使うだけでアンサンブルのような効果が得られるということです。ただし、自己蒸留はあくまでアンサンブルを模倣することで推論時間を減らしているだけなので推論時もそのままアンサンブルを用いる方が基本的には良い性能を示します。最後にこの自己蒸留を加えたネットワークの図を示して実験結果へと移ります。先ほどのアンサンブルの図にSelf-distillation(自己蒸留)が加えられているだけです。
2. SLAの実験結果
実験は大きく分けて以下の3つです。
- アブレーションスタディ
- 画像分類
- 特殊なデータでの画像分類(Few-shotやimbalancedなど)
2.1 アブレーションスタディ
早速アブレーションスタディからです。ここではSLAの有用性を見るために次の2つを行います。
- DAとマルチタスク(SSL)との比較
- 他アンサンブル手法との比較
2.1.1 DAとマルチタスク(SSL)との比較
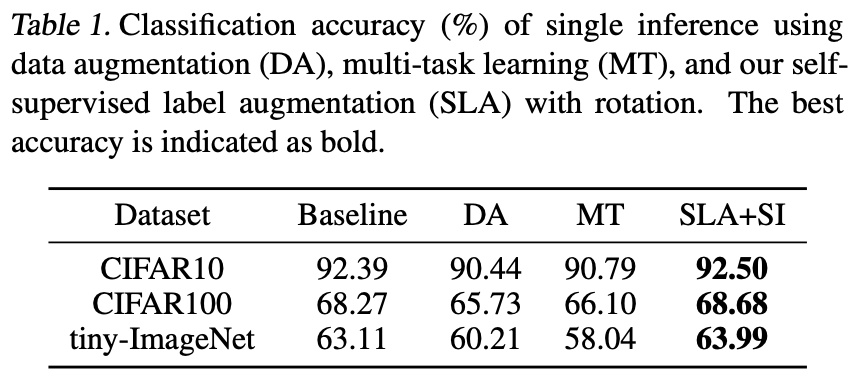
まずはSLAを他の学習方法と比較します。上表のそれぞれの列の意味は次の通りです。
- Baseline: ランダムクロップ+水平反転適用し学習させたモデル
- DA: 回転を適用し学習させたモデル
- MT: SSLのこと。回転角度とラベルの2つをそれぞれ予測できるようにしたモデル。
- SLA+SI: 提案手法。推論時は回転を加えていない画像の予測ラベルのみを用いる。(=SI)
上表を見ると他の学習手法では性能劣化が起きてしまっていますが、提案手法のみがベースラインをわずかに改善させていることがわかります。
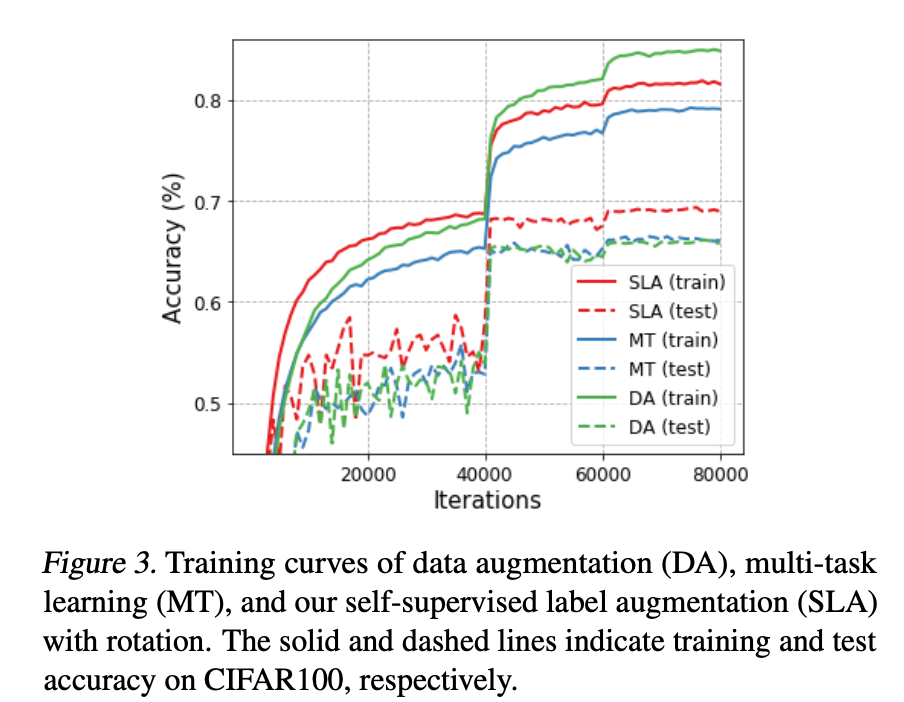
上図はCIFAR100における各学習方法の学習過程を示しています。実線は学習時の精度で、点線は推論時の精度です。論文中では、「推論時にDAの精度が低いのはDAが不要な一貫性をモデルに強制しているため」であるとしています。
2.1.2 他アンサンブル手法との比較

続いて、SLAを他アンサンブル手法と比較してみます。1.2.2のアンサンブルにて説明したように、SLAには各回転角度での推論結果から最終的な意味ラベルを1つ予測するアンサンブルのような機構があります。上表ではAGと表されています。またIEとはIndependent Ensembleの略で、単に4つのモデルを用いたアンサンブルとの比較も行っています。(回転を用いた場合にAGでは4つの回転角度から予測を決定するため。)
上表を見るとSLA+AGはベースラインをしっかりと改善させていますが、このSLA+AGがIEと同程度の性能を示していることがもっと驚きです。SLA+AGを4つのモデルで行う(=IE+SLA+AG)ことでさらなる性能向上を達成しています。

さらにテスト時のアンサンブルとも称されるten-cropとの比較も行っています。ten-cropは1枚の画像から10個のクロップを生成しそれぞれに対するsoftmaxを平均して最終出力とするものです。クロップ版AGのようなものですね。ten-cropにも見事SLA+AGが勝ってますね。
2.2 画像分類
それでは、実際の画像分類タスクにおけるSLAの有用性を見ていきます。次の3つを行います。
- 画像分類における実験結果
- DAの数
- 他手法との組み合わせ
2.2.1 画像分類における実験結果
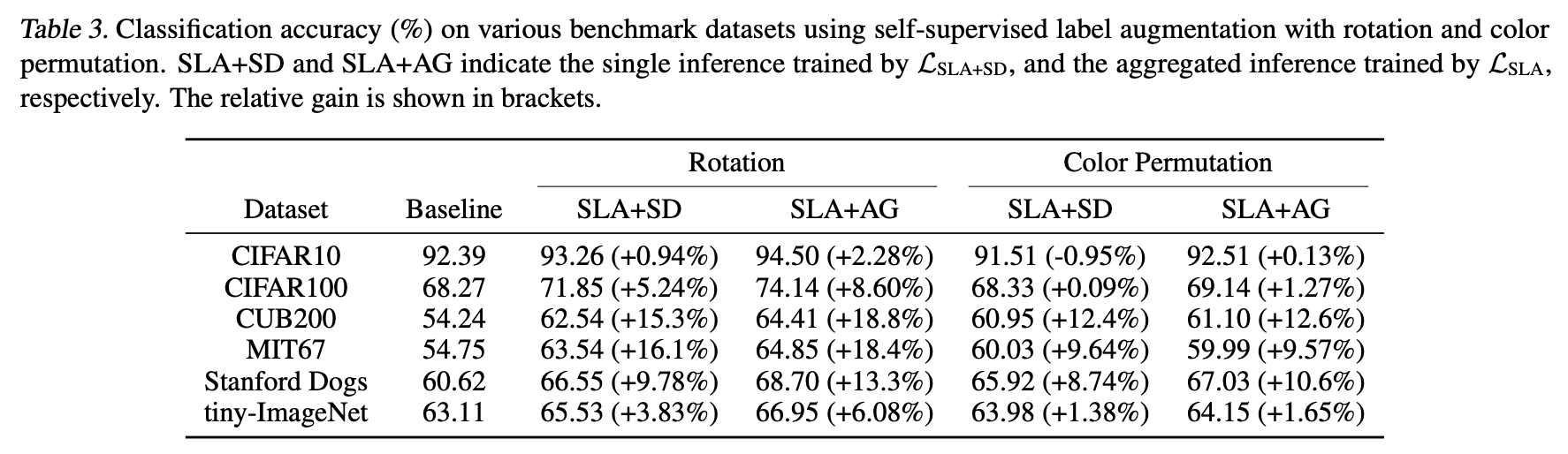
上表では、回転とRGB入れ替えの場合それぞれについての各データセットでの識別精度をまとめています。ネットワークにはCIFAR10/100にはResNet32を、それ以外にはResNet18を用いています。ここから言えることは次の2つです。
- SLAを使うことでどのデータセットでも分類精度が向上
- AGほどではないもののSelf-Distillation(=SD)でもある程度のゲインを得られる。
2.2.2 DAの数
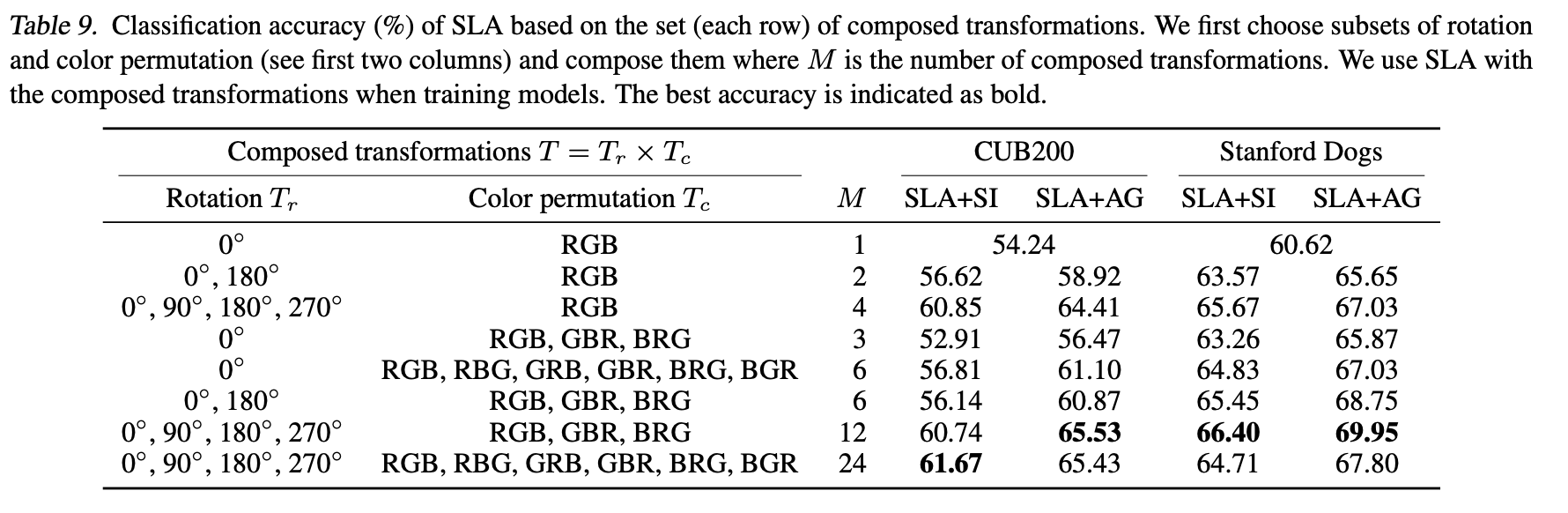
ここでは回転とRGB入れ替えの両方を一気に適用した場合を考えます。その時、回転角度やRGB入れ替えのパターンなどの一部だけを用いた場合についても同時に見ていきます。上表では回転角度とRGBのそれぞれのパターンとそれによる組み合わせの数(=$M$)が記されています。上表を見ると、回転角度は4つ全て用いてRGBの入れ替えに関しては3パターンを用いる合計12個の組み合わせ($M=4\times3=12$)のときが最も良い性能を示していることが分かります。
2.2.3 他手法との組み合わせ
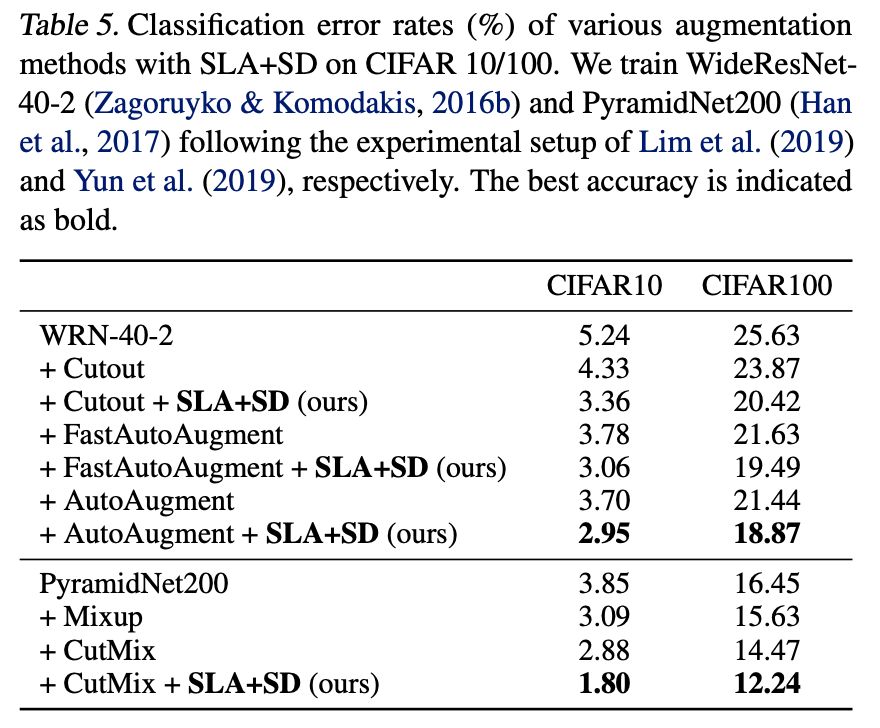
さらに他DA手法たちと同時に使った場合に識別精度がどうなるのかについても見てみます。上表を見ると、CutoutやCutMix、AutoAugmentなど比較的最近のDA手法と一緒にSLAを用いることでさらなるゲインが得られることがわかります。
2.3 特殊なデータでの画像分類
続いて特殊なデータセットで画像分類を行います。実験設定は次の4つです。
- データ数が少ない場合
- Few-shot
- 不均衡データ
- ラベル数が多い場合
2.3.1 データ数が少ない場合

まずは各クラスごとのデータ数が少ない場合について検証してみます。上図はSLAのAG(赤)とSD(青)を用いた場合を示しています。ここではBaseline(黒)との相対的な性能向上が示されています。この相対的な性能向上はデータ数が少ないほど(表の左側ほど)、SLAの相対的ゲインが大きいことがわかります。そのためデータ数が少ない場合にもSLAはより上手に対応してくれることがわかります。
2.3.2 Few-shot
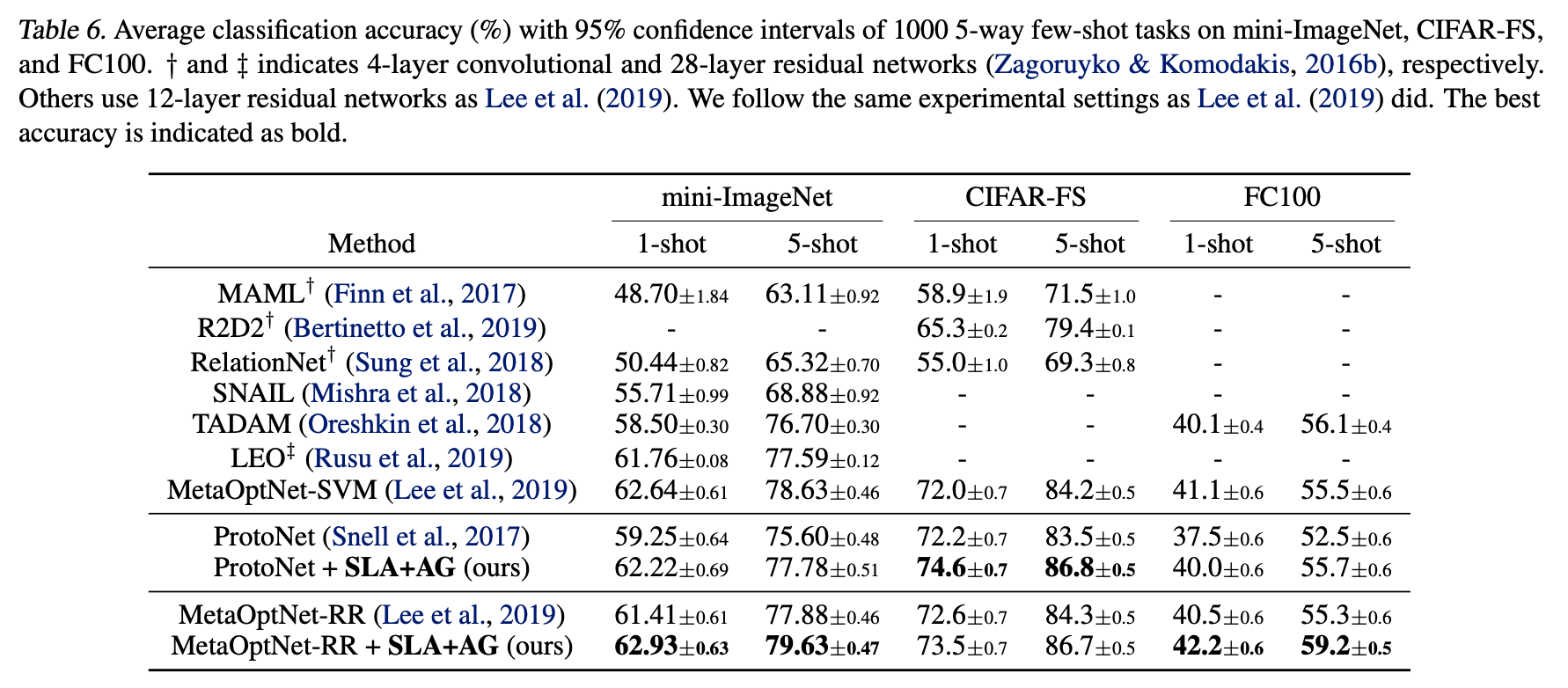
データ数が少ない場合にSLAが比較的よく働いてくれることから、Few-shotでも性能向上を果たしてくれそうです。上表はそれをまとめたもので、予想通りSLAを用いることでFew-shotでもゲインが得られていることが分かります(ProtoNet/MetaOptNet)。
2.3.3 不均衡データ

不均衡データ(=クラスごとのデータ数が大きく異なるデータ)に対してもSLAがゲインをもたらしていますね。
2.3.4 ラベル数が多い

そして最後にむしろラベル数が多い場合(ImageNet:1000ラベル、iNaturalist: 8,000ラベル)でもSLAがうまくいくのかを見てみます。そもそものラベル数が多いと、結合ラベルはDAとの組み合わせなのでものすごく大きくなりうまく学習できなさそうですが、実際のところはSLAを用いると性能が上がっています。やはりSLA+AGがもっとも良いですね。
3. まとめと所感
SLAは、結合ラベルという新たなラベルを導入することで性能向上を果たしました。本論文では画像分野に対する実験のみでしたが、SLAの考え方はどの分野にも使えるものであり今後のさらなる発展が気になります。PyTorchによる公式実装もありますので試してみてはいかがでしょうか!
Twitterで人工知能のことや他媒体の記事などを紹介していますので@omiita_atiimoもご覧ください。
こちらもどうぞ:



