ABC432 E - Clamp
https://atcoder.jp/contests/abc432/tasks/abc432_e
E問題も解いてきました。セグメントツリーが必要と思いきやフェニック木(Fenwick Tree, Binary Indexed Tree)で解けるということだったので今回はそれを使って解きました。フェニック木は学習したことがあるのでもし思い出せていたら解けていたのかな……とも思いましたが、今の自分には思いつけない使い方をしていたのでどの道無理だったことがわかりました。
考察
$ max(l, min(r, A_i)) $ という一見単純だけど実はややこしい式に面食らいます。3変数の大小関係によって6通りに分けてそれぞれ答えを求めて……としたところで、等しい場合もあることに気づきます。そして、よくよく制約を見ると $ l \leq r $ が保証されていないことにも気づきます。じゃあなぜ $ l, r $ という変数名にしたのか……と、泣き言を言っても仕方ありませんね。等号が入ると一気に場合分けが複雑になりますが、ともかく入力される $ l, r $ の大小関係を起点に場合分けを考えてみます。
l = r の場合
- l = r < A[i] なら l
- l = r = A[i] なら l
- l = r > A[i] なら l
よく考えてみると最後に l との max をとるので当たり前ですね。
l > r の場合
同様に全て l になります。
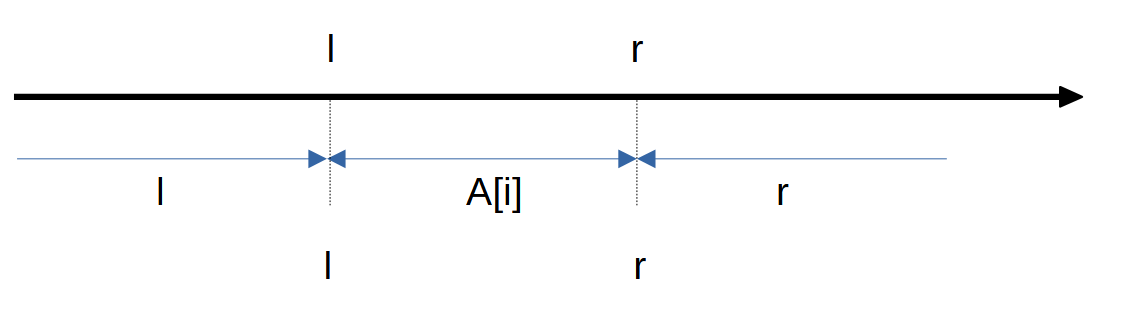
l < r の場合
丁寧に見ていきます。図にするとわかりやすいですね。つまり l 以下のものは全て l になり、r 以上のものは全て r になり、その間のものは A[i] のままです。
問題は実装です。これを高速に求められるデータ構造がわかりませんでした。こういういろんな計算ができるのはたぶんセグメントツリーかな、使い方わからんけど……と思って諦めました。早く勉強しないといけませんね。
Fenwick Tree
セグメントツリーではなくFenwick Treeを利用しても解けるそうです。概要としては追加と区間和が O(logN) でできるデータ構造ということなのですが、いろいろと応用が効きます。仕組みについてはわかりやすい解説がありました。とてもありがたいですね。
詳しくはこちらを読んでいただくとして……ともかく追加、区間和の2つの操作を応用して次のような計算が出来ます。
「何の数字が何個あるか」を Fenwick Tree の要素にする
この工夫をするだけで x 以上/以下/より大/未満 のものが何個あるかを求められるようになります。1が何個ある、2が何個ある、3が何個ある……という情報がわかっているときに sum で区間和を求めればそれらの合計が求められるわけですね。例えば配列 A に含まれる x 以下の数字の個数を求めたいなら [0, x] の範囲で和を求めればいいです。コードを読んでいただいた方がわかりやすいかもしれません。
# 配列に格納する
B = [42, 1, 42, 5, 88, 17, 73, 42, 5, 88, 17, 73, 42, 50, 88, 17, 73, 42, 5, 100]
N, M = len(B), max(B)
ft1 = fenwicktree.FenwickTree(M+1)
for b in B:
ft1.add(b, 1) # 個数を調べたいので1を足す
def leq(fw, x):# X 以下の値が何個あるか
return fw.sum(0, x+1)
def lthan(fw, x):# X 未満の値が何個あるか
return fw.sum(0, x)
def geq(n, fw, x):# X 以上の値が何個あるか
return n - fw.sum(0, x)
def gthan(n, fw, x):# X より大の値が何個あるか
return n - fw.sum(0, x+1)
「何の数字が何個あるか」に「数字の値」を掛けたものを Fenwick Tree の要素にする
こちらは l 以上 r 以下の値の合計値を求めるといったことが可能になります。
# 配列に格納する
B = [42, 1, 42, 5, 88, 17, 73, 42, 5, 88, 17, 73, 42, 50, 88, 17, 73, 42, 5, 100]
N, M = len(B), max(B)
ft2 = fenwicktree.FenwickTree(M+1)
for b in B:
ft2.add(b, b) # その値の合計値を調べたいので自分自身の値を足す
def sum_between(fw, l, r): # l 以上 r 以下の値を合計する
return fw.sum(l, r+1)
使用条件
ただしこれらの用法には制限があります。とりうる値全てについて「何の数字が何個あるか」を格納するわけですから、値域の分だけの大きさの配列を作る必要があります。今回の問題は $ 1 \leq A_i \leq 5 \times 10^5 $ という制約のおかげで Fenwick Tree が使えますが、この便利なデータ構造はいつでも使えるわけではありません。問題によっては座標圧縮をするなどの工夫が必要になることもあると思います。
実装
この仕組みを利用して、クエリ2が与えられたときの配列 A について
- l 以下の要素の数を計算し、l を掛ける
- r 以上の要素の数を計算し、r を掛ける
- l < A[i] < r となるような A[i] の総和を求める
これらの計算が高速に行えます。
from atcoder import fenwicktree
def leq(fw, x):# X 以下の値が何個あるか
return fw.sum(0, x+1)
def lthan(fw, x):# X 未満の値が何個あるか
return fw.sum(0, x)
def geq(n, fw, x):# X 以上の値が何個あるか
return n - fw.sum(0, x)
def gthan(n, fw, x):# X より大の値が何個あるか
return n - fw.sum(0, x+1)
def sum_between(fw, l, r): # l 以上 r 以下の値を合計する
return fw.sum(l, r+1)
N, Q = map(int, input().split())
A = list(map(int, input().split()))
ans = []
M = 5 * 10**5
ft1 = fenwicktree.FenwickTree(M+1) # (1) 個数管理用
ft2 = fenwicktree.FenwickTree(M+1) # (2) 範囲内の A[i] の和の計算用
for a in A:
ft1.add(a, 1) # 個数を調べたいので1を足すだけ
ft2.add(a, a) # そこまでの合計値なので自分自身を足す
for _ in range(Q):
query = list(map(int, input().split()))
if query[0] == 1:
x, y = query[1], query[2]
x -= 1 # 1-indexで与えられるので
ft1.add(A[x], -1)
ft1.add(y, 1)
ft2.add(A[x], -A[x])
ft2.add(y, y)
A[x] = y
elif query[0] == 2:
l, r = query[1], query[2]
if l >= r:
tmp_ans = N * l
elif l < r:
tmp_ans = leq(ft1, l) * l + geq(N, ft1, r) * r
tmp_ans += sum_between(ft2, l+1, r-1)
ans.append(tmp_ans)
for an in ans:
print(an)
まとめ
Fenwick Tree の活用法を知らなかったので今回の問題を解けませんでしたが、これで解けるようになったはずです。うまく活用したいですね。