ABC432 C - Candy Tribulation
https://atcoder.jp/contests/abc432/tasks/abc432_c
今回はABCの3完でした。Dは激難で手も足も出ず、Eはセグメントツリーが必要そうだと推測できたものの、肝心のセグメントツリーの使い方をまだ理解していないのでギブアップしました。パフォーマンスは1000ちょっとでレートも横ばいの+1でした。レートが落ちなかっただけありがたいですね。
考察
ぱっと見よくわからなかったのでまずは愚直に考えました。N 人それぞれについて、X, Y を計 A[i] 個組み合わせて作れる重量の一覧を出す。N 人全てについて、共通の値があればその中の大きな飴が最大になるやつが答え。
次に入力例1を用いて作れる値を書き出してみることにしました。
N, X, Y = 3, 6, 8
A = [11, 10, 13]
- 11個ある場合は全部大きな飴にしたら88。全部小さな飴にしたら66。1個ずつ交換していけば2刻みに作れる。
- 10個ある場合は全部大きな飴にしたら80。全部小さな飴にしたら60。1個ずつ交換していけば2刻みに作れる。
- 13個ある場合は全部大きな飴にしたら104。全部小さな飴にしたら78。1個ずつ交換していけば2刻みに作れる。
書き出している間にすぐ気づきました。つるかめ算ですね。大きな飴を1個ずつ小さな飴に交換していくというのがまさにつるかめ算です。
つるかめ算
よく知られているので今更ですが、つるかめ算では
- 与えられた頭の合計数を用いて、全てが亀だと仮定した場合の脚の本数の合計を計算する。
- 与えられた実際の脚の合計本数と比較して差を計算する。
- 1匹入れ替えるたびに鶴と亀の脚の本数差(2本)だけ脚の合計本数が変化するので1匹ずつ入れ替えていく。
- 割り算を使うことで 3. の操作を高速化できる。
こんな流れの処理を行います。この問題はまさにこれですね。大きな飴を1個小さな飴に交換するたびに合計の重量が Y-X だけ減ります。
条件を満たすかどうか?
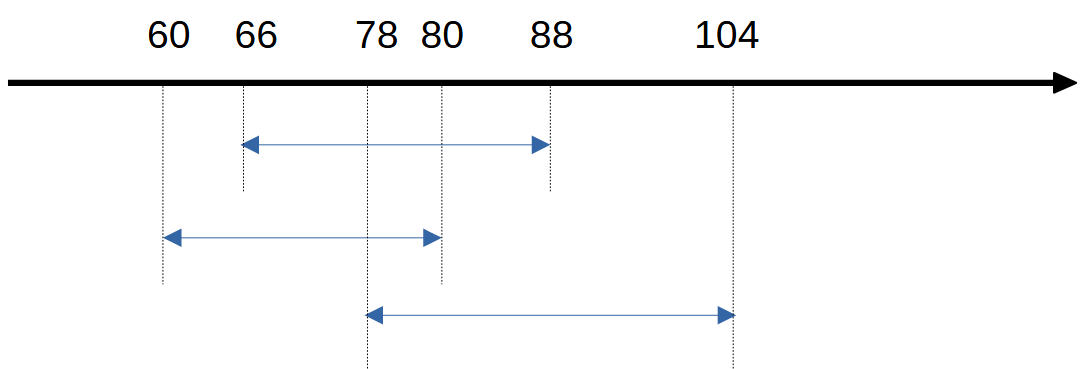
入力例1の範囲を図示するとこうなります。
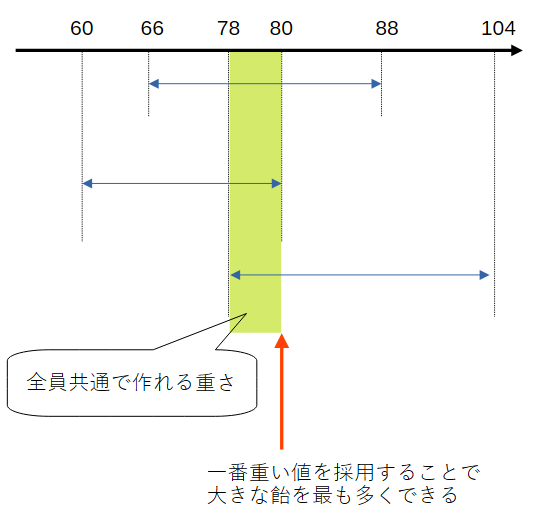
全ての範囲がカバーするようなところがあればそこが答えです。複数の値が該当する場合、最も大きな値が答えになります。配る飴の総数は決まっていますから、総重量をなるべく大きくした方が大きな飴が多くなります。
また、一つでも範囲の重ならない矢印があれば条件を満たす配り方は存在しません。最も厳しいケースを想定し、一番左にある「矢印の右端」と一番右にある「矢印の左端」に着目します。
$$ 一番左にある「矢印の右端」 < 一番右にある「矢印の左端」$$
になるとき、全員に共通するような範囲はできませんね。数式でいうと
$$ min(A) \times Y < max(A) \times X $$
です。
作れる総重量を求める
重なることがわかったら、その中で最大の値を求めます。一番左にある「矢印の右端」つまり $ min(A) \times Y $ が作れる一人あたりの最大の重さになりますね。
……ここでコードを書いて提出したら 2 つの WA が出てしまいました。焦ります。しばらく考えているうちに「Y-X 刻み」を思い出しました。上で書いた矢印は連続した値ではなく Y-X 飛ばしなので、ここが噛み合わなければ答えは合いません。
mod (Y-X) を考える
N 人のそれぞれについて、作れる重さの mod (Y-X) がどうなるかを調べます。次のケースを試してみます。
N, X, Y = 3, 5, 8
A = [11, 10, 13]
- 11個ある場合は 55 から 88。mod 3 は1。
- 10個ある場合は 50 から 80。mod 3 は2。
- 13個ある場合は 65 から 104。mod 3 は2。
Y-X 刻みの重さが作れるので、ある人が作れる重さの値の mod (Y-X) は全て同じになります。つまり1人につき1つ調べれば十分で、またこの値が違う人同士で同じ重さを作ることはできません。なので、全員の mod が一致している場合以外は答えが -1 となります。
というわけで「全ての矢印がカバーする範囲はあるか」「全員の mod (Y-X) が一致しているか」を判定し、どちらも満たしていれば結果の計算をします。
結果の計算
先に図示したように全員の重さを一番左にある「矢印の右端」、つまり $ min(A) \times Y $になるようにします。つるかめ算に基づき、
- まず小さな飴を A[i] 個配ることにする。
- そこから何個の飴を大きな飴に取り替えれば重さが $ min(A) \times Y $ になるか計算する。(割り算で簡単にできる)
これを N 人について繰り返して大きな飴に交換した数を足し合わせれば答えが出ます。
N, X, Y = map(int, input().split())
A = list(map(int, input().split()))
if Y * min(A) < X * max(A):
print(-1)
else:
# 作れる重量は Y-X ごとなので mod (Y-X) を考えないといけない。
S = set()
z = Y-X
for i in range(N):
S.add((X*A[i]) % z)
if len(S) > 1:
print(-1)
else:
# 作れる場合、統一するグラム数は Y * A[i] の中の最小のものに引っ張られる。
g = Y * min(A)
# あとはつるかめ算
ans = 0
for i in range(N):
ans += (g - X * A[i]) // (Y-X)
print(ans)