More than 5 years have passed since last update.

カオスな写像で遊んでみた

Last updated at 2017-09-26Posted at 2017-09-24

テント写像,ロジスティック写像などの分布を画像化

テント写像

x_{n+1} =\left\{
\begin{array}{ll}
ax_{n} & (0 \leq x \leq \frac{1}{2}) \\
a(1-x_{n}) & (\frac{1}{2} \lt x_{n} \leq 1)
\end{array}
\right.

ロジスティック写像


x_{n+1} = \begin{array}{ll} ax_{n}(1-x_{n}) & (0 \leq x \leq 1) \end{array}

この2つをまとめると


x_{n+1} = \begin{array}{ll} k \{1-(| 1-2x_{n} |)^p\} & (0 \leq x \leq 1) \end{array}

となる
k=a/2 , p=1とおくとテント写像
k=a/4 , p=2とおくとロジスティック写像

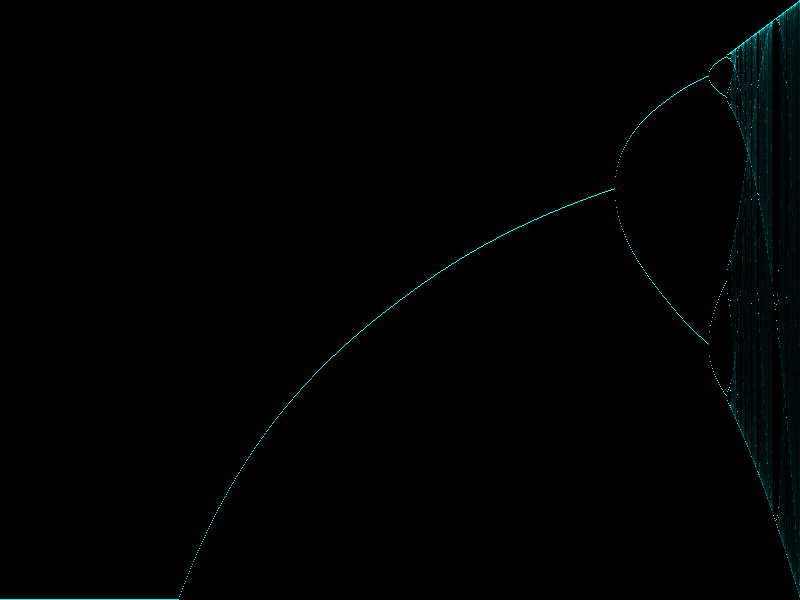
pを固定しkを0から1まで変化させていった場合の分布の変化をMagickWandで画像化した
適当なxの初期値からスタートしてn=100までは捨てて
それ以降の10000個のデータの分布を使った

余興で複数組み合わせて使った場合のものも作った
その1


\begin{align}
a_{n+1} &=　k \bigl\{ b_{n} \{1-(| 1-2a_{n} |)\} + (1-b_{n}) \{1-(| 1-2a_{n} |)^2\} \bigr\} \\
b_{n+1} &= (1-b_{n}) \{1-(| 1-2a_{n} |)\} + b_{n} \{1-(| 1-2a_{n} |)^2\}
\end{align}

その2


\begin{align}
a_{n+1} &=　k \bigl\{ 
b_{n} c_{n} \{1-(| 1-2a_{n} |)\} + 
b_{n} (1 - c_{n}) \{1-(| 1-2a_{n} |)^2\} + 
(1 - b_{n}) d_{n} \{1-(| 1-2a_{n} |)^3\} + 
(1 - b_{n}) (1 - d_{n}) \{1-(| 1-2a_{n} |)^4\} \bigr\} \\
b_{n+1} &= 
b_{n} (1 - c_{n}) \{1-(| 1-2a_{n} |)\} + 
(1 - b_{n}) d_{n} \{1-(| 1-2a_{n} |)^2\} + 
(1 - b_{n}) (1 - d_{n}) \{1-(| 1-2a_{n} |)^3\} + 
b_{n} c_{n} \{1-(| 1-2a_{n} |)^4\} \\

c_{n+1} &= 
(1 - b_{n}) d_{n} \{1-(| 1-2a_{n} |)\} + 
(1 - b_{n}) (1 - d_{n}) \{1-(| 1-2a_{n} |)^2\} + 
b_{n} c_{n} \{1-(| 1-2a_{n} |)^3\} + 
b_{n} (1 - c_{n}) \{1-(| 1-2a_{n} |)^4\} \\

d_{n+1} &= 
(1 - b_{n}) (1 - d_{n}) \{1 - (| 1 - 2a_{n} |)\} + 
b_{n} c_{n} \{1 - (| 1 - 2a_{n} |)^2\} + 
b_{n} (1 - c_{n}) \{1 - (| 1 - 2a_{n} |)^3\} + 
(1 - b_{n}) d_{n} \{1 - (| 1 - 2a_{n} |)^4\}
\end{align}

###ソースコード
https://github.com/2a3oiUA3zfDtr3py/Misc/tree/master/Chaotic_Maps

###結果

p=0.75