PCR検査の偽陽性のせいでコロナ騒動が永遠に終息しない可能性がある件

はじめに

　新型コロナウイルス感染症(COVID-19)は2020年6月7日現在、感染者7百万人、死者40万人を突破し、人類史上稀にみる世界的パンデミックとなりました。日本では、緊急事態宣言宣言（4/7～5/25）による”国民的自粛”により、一時は743人/日(4/12)まで拡大していた感染が、31人/日(5/25)まで抑制されました。しかし、世界を見てみると未だに感染拡大が続いており、いつ終息を迎えるのか大変不透明です。
　日本の緩い自粛と当初の厳しい受診基準には様々な批判がありました。一方で、一部の国ではドライブスルー検査などを活用し、兎に角検査数を増やすことを最優先にしている政策がとられています。ある記事では、アメリカが人口千人あたり16.4人の検査をしているのに対し、日本では1.8人に過ぎないとの指摘がされています。
　しかし、新型コロナウイルスの確定診断にはPCR検査を用いられているものの、その精度（感度・特異度）については論争があります。本記事では、"むやみに検査数を増やす政策"を取った場合、PCR検査の偽陽性によって、新型コロナウイルス騒動が永遠に終息しないという事態が起こりうることを指摘したいと思います。計算の手段として、SEIRモデルを使いPythonでシミュレーションします。

世界各国の状況

　まず、世界各国の現在のCOVID-19の状況を見てみます。計算方法は、こちらの記事やこちらの記事を参照してください。下図は、世界の地域別の実効再生産数(Rt)の推移を計算したグラフです。縦軸がRt、横軸が累積感染者数です。

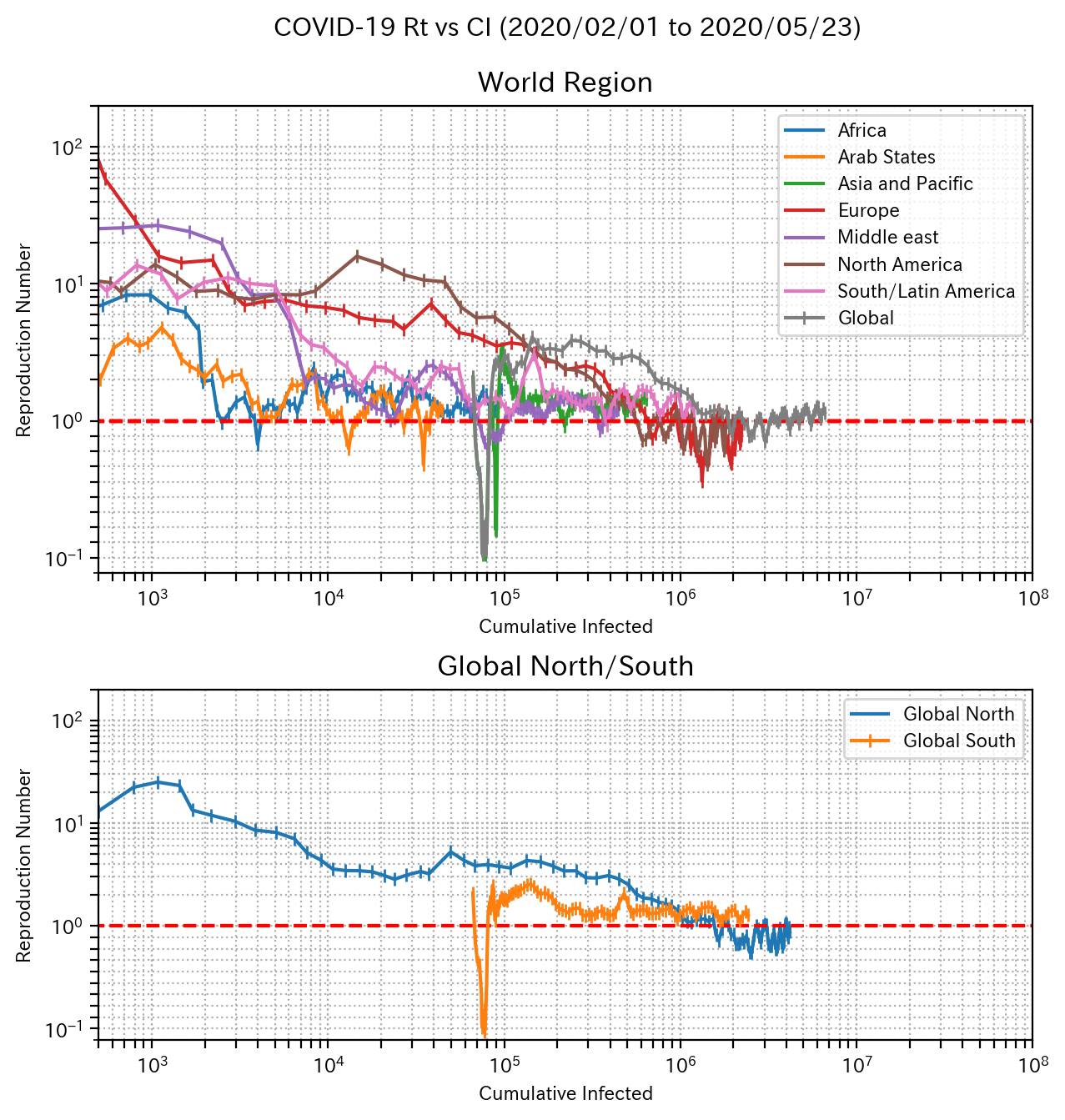
　世界を７つの地域に分類しそれぞれの地域で感染者数を集計して実効再生産数を求めています。地域によって１に到達するまでの早さに差がありますが、ほぼ1～1.5付近に収束している様子が分かります。ここで疑問なのが、地域による差が収束値に何故現れないのか？という点です。
　次に、医療面での状況を見てみます。下図は、横軸を累積感染者数、左図の縦軸は死亡率（死亡者数／要治療者数）、右図の縦軸は回復率（回復者数／要治療者数）をそれぞれ取っています。

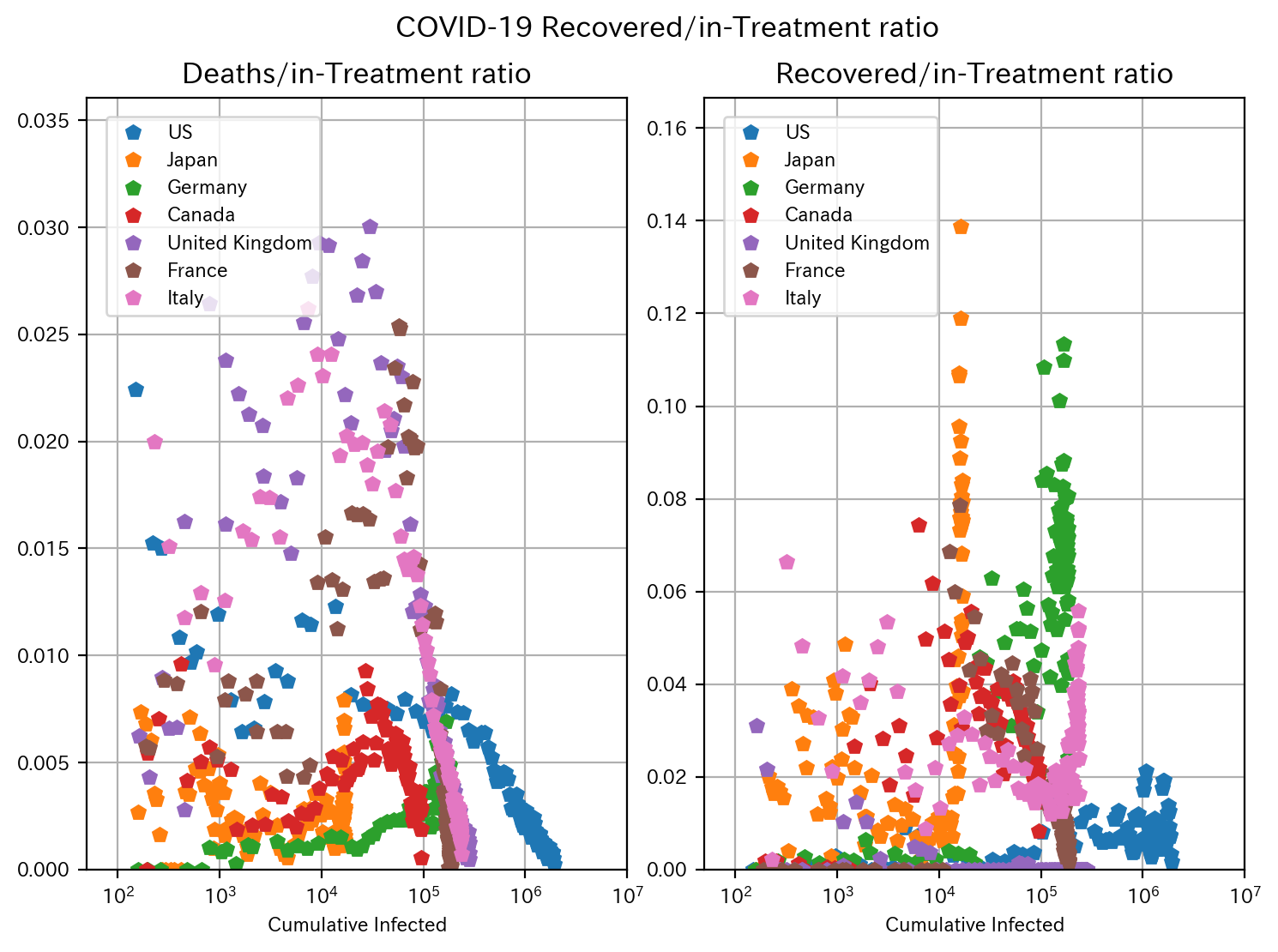
　注目すべき点として、以下２点挙げます。

• アメリカ、イギリス、フランス、イタリア、カナダでは、累積感染者数が増えるにつれて死亡率が0付近にまで下がっているのに対し、日本、ドイツではむしろ逆の傾向。
• 日本、ドイツ、イタリアでは、累積感染者数が増えるにつれて回復率が急上昇している。

医療アクセスが比較的良好な日本、ドイツで死亡率が上昇し、その他の国で死亡率が下がり、ほとんど死亡率が０になっている国があるのは何故でしょうか？アビガン、レムデシビルなどの治療薬の治験や承認が進んでいると言っても、日本やドイツで使えない訳ではないので、治療技術の改善効果とは考えにくいですね。また死亡率の計算は、要治療者数を分母にしているので、累積感染者数が増えれば下がるという単純な関係でもありません。SARS-Cov-2が急に弱毒化？という報告も聞きません。

PCR検査の偽陽性による影響という仮説

　上記の不思議な２つの現象、1.実効再生産数が地域によらずほぼ1に収束している、2.感染者数が増加するにつれ死亡率が0まで落ちている国がある、を説明する仮説として、PCR検査の偽陽性を考えてみたいと思います。
　その検証のため、SEIRモデルに基づくシミュレーションを行います。まず、以下の変数を導入します。
　

• S:感染症に対して免疫を持たない者(Susceptible)
• E:感染症が潜伏期間中の者(Exposed)
• I1:真の発症者(Truely Infectious)
• I2:PCR検査の偽陽性により感染者とされた者(Fakely Infectious)
• R:感染症（偽陽性含む）から回復し免疫を獲得した者(Recovered)。
• D:PCR検査数

また、パラメータとして、次を導入します。

• R0:基本再生産数（2.5を採用）
• lp:潜伏期間（5日を採用）
• ip:感染期間（8日を採用）　
• $\beta$:感染率($\beta=R_0/(S_0 *ip)$)
• k1:検査実施倍率(=1/陽性率)（10を採用）
• k2:真の感染者(I1)の検査捕捉率（0.2を採用）
• f1:PCR検査の偽陽性率

PCR検査数Dに関して、以下の仮定を置きます。

1. 検査実倍率k1に関しては、陽性率が10%になるようにコントロールされる。すなわち、陽性者数に応じて検査数Dが増減する。
2. 真の感染者(I1)の検査捕捉率k2は20%とする。
3. 検査数Dのうち、比率f1で偽陽性I2が生じる。

計算モデル

　以上の仮定のもと、計算モデルを記述します。

\begin{eqnarray}
\beta &=& \frac{R_0}{ip S_0} \\
\frac{dS}{dt} &=& - \beta S \cdot I \\
\frac{dE}{dt} &=& -\frac{dS}{dt} - \frac{1}{lp} E \\
\frac{dI_1}{dt} &=& \frac{1}{lp} E - \frac{1}{ip} I_1 \\
\frac{dI_2}{dt} &=& f_1 D - \frac{1}{ip} I_2 \\
\frac{dR}{dt} &=& \frac{1}{ip} (I_1 + I_2) \\
\frac{dD}{dt} &=& k_1 \left(k_2 \frac{dI_1}{dt} +\frac{dI_2}{dt} \right) 
\end{eqnarray}

最後の行で、陽性率に基づく検査数のコントロールをしています。また、偽陽性者も感染期間経過後に真の感染者同様に回復するものとしています。
また、この非線形微分方程式の中から、$I_2,D$に関する部分だけ取り出し、$I_1$を無視すると、

\begin{eqnarray}
\frac{d}{dt}\left(
\begin{array}{c}
I_2 \\
D
\end{array} 
\right)
=
A\left(
\begin{array}{c}
I_2 \\
D
\end{array} 
\right),\ 
A=
\left(
\begin{array}{cc}
-\frac{1}{ip} & f_1 \\
-\frac{k_1}{ip} & k_1 f_1 
\end{array} 
\right)
\end{eqnarray}

となりますが、この行列$A$の0でない固有値を次式で置きます。

e(A) = k_1 f_1 - \frac{1}{ip}

計算結果

今回は、結果から先に示したいと思います。初期状態を$(S,E,I_1,I_2,R,D)=(1000,0,1,0,0,0)$とします。

偽陽性率f1=0のとき

PCR検査の偽陽性が全くない場合です。最終的に894人が感染者としてカウントされます。

偽陽性率f1=0.0047(=0.47%)のとき

PCR検査の偽陽性率が0.47%の場合です。最終的に998人（ほぼ全員）が感染者としてカウントされます。

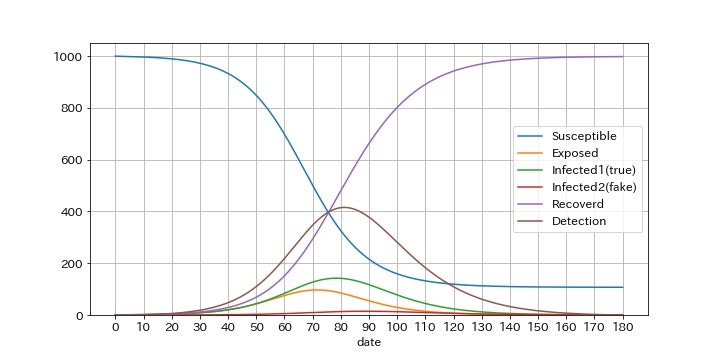
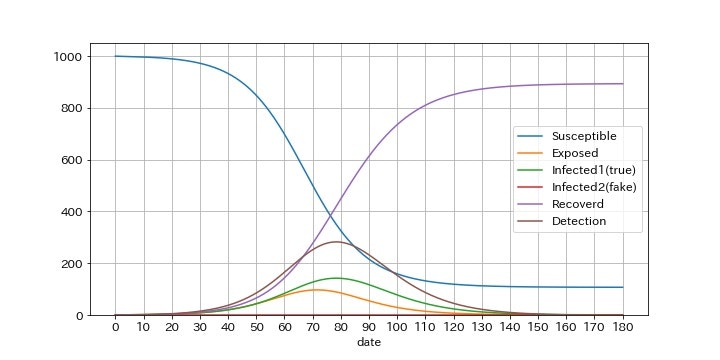
偽陽性率f1=0.0125(=1.25%)のとき

PCR検査の偽陽性率が1.25%の場合です。最終的に3059人！（3倍）が感染者としてカウントされます。

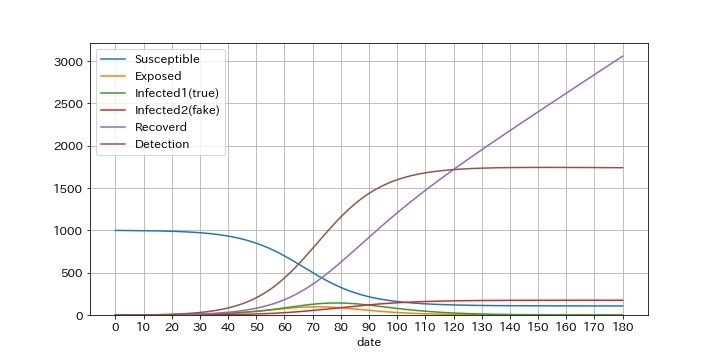
グラフで特に注目すべき点は、偽陽性による感染者数I2と検査数Dがほぼ一定となっている点です。この状態であれば、感染者数が一定なので、見かけ上、実効再生産数Rt=1となります。つまり、一人の感染者が生み出す感染者は一人なので増えも減りもしません。

偽陽性率f1と最終的な感染者数の関係

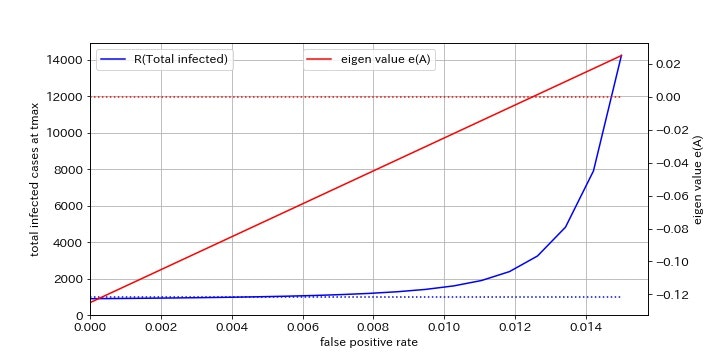
PCR検査の偽陽性率$f_1$と最終的な感染者数$R(T_{max})$の関係をグラフにしてみます。
このとき、先ほどの行列$A$の固有値$e(A)$も同時にプロットします。

偽陽性率が上昇するにつれて、最終的な感染者数が指数的に増加していきます。$f_1=0.0047$付近で$S_0=1000$と交差しています。また、$f_1=0.0125$のとき$e(A)=0$となります。これは計算式$e(A) = k_1 f_1 - \frac{1}{ip} = 0$から$f_1$を解くと得られる値$f_1=\frac{1}{k_1 \cdot ip}$です。

考察

以上から、SEIRモデルに基づく、PCR検査の偽陽性がもたらす影響に関して、次の傾向がシミュレーションから導けます。

• 偽陽性率がある値(0.47%)を超えると、ほぼ全員が感染している（と検知されてしまう）状態になる。
• 偽陽性率がある値(1.25%)を超えると、真陽性者が0であるにも関わらず、実効再生産数$Rt\geq1$が永遠に継続して終息しない状態に陥る。この1.25%という数字は、**(検査陽性率)/(感染期間)**で決まる。
• 上記の状態が現実に起きているとすると、アメリカ、イタリアなどで死亡率が0まで低下している現象を説明できる。
• 上記の状態は、偽陽性の罠あるいは陽性率維持の罠とでも呼ぶべき現象であり、早急に対策が必要である。

さらに言えば・・・

• じゃあ、PCR検査で偽陽性はいくらなのか？という疑問が湧きますが、はっきりした数字は分かりませんでした。マラリア試薬の評価において、顕微鏡とPCR検査を比較した結果では感度80～98%、特異度96～100%とあります。つまり、顕微鏡で白黒はっきり分かるマラリア検査においても4%程度の偽陽性率は生じていることが分かります。
• 新型コロナウイルスの感度、特異度はそれより低いと考えられます。感度は70％程度と言われています。
• 「細胞中で産生されるウイルス量がインフルエンザウイルスの約100分の1」との指摘があります（こちら）。PCR検査はそもそもウイルスの特定領域を増幅することで感度を上げる検査なので、増幅率が100倍以下ならインフルエンザウイルスと同量にしかなりません。症状が似ている新型コロナに罹患したと思い検査したらインフルエンザウイルスに反応した、ということであれば偽陽性は十分生じえますよね。特に電気泳動によるPCRの場合。
• また、こちらの記事では、リアルタイムPCRで偽陽性が生じる原因として、「リアルタイムPCR増幅曲線の陰性と陽性のギリギリのラインを読む」ことで誤判定が起きうると指摘されています。
• テレビでは、「とにかく検査！」、「検査をいくらでも増やすべき！」とコメンテーターが叫んでいますが、上記の偽陽性の罠を踏まえれば、意味がないどころか、コロナの終息を阻害して日本経済をダメにしかねません。
• こちらの記事で指摘したとおり、事前確率が十分高くない検査は嘘陽性（≠偽陽性）が高く無意味ですね。

参考リンク

下記のページを参考にさせて頂きました。

1. 新型コロナ、日本のPCR検査数はOECD加盟国36カ国中35位。世界と比べても際立つ少なさ
2. 新型コロナウイルスの実効再生産数の世界動向から収束時期を検討してみる
3. 新型コロナウイルスの医療崩壊仮説を検証してみる
4. 新型コロナウイルス対策としての休業の効果をSEIRモデルで検証
5. 厚労省：マラリア抗原検出試薬
6. 緊急寄稿（1）新型コロナウイルス感染症（COVID-19）のウイルス学的特徴と感染様式の考察
7. ベイズの定理で理解する新型コロナウイルスへのPCR検査の検査対象を絞る意義
8. PCR論争に寄せて─PCR検査を行っている立場から検査の飛躍的増大を求める声に
9. 臨床検査医学会栁原氏、新型コロナのPCR検査が増えない3つの理由

Pythonコード

最後に、本記事で使用したPythonコードを貼っておきます。

import numpy as np
import matplotlib.pyplot as plt

def my_odeint(deq, ini_state, tseq, keys):
    sim = None
    v = np.array(ini_state).astype(np.float64)
    dt = (tseq[1] - tseq[0])*1.0
    for t in tseq:
        dv = deq(v,t, keys)
        v = v + np.array(dv) * dt
        if sim is None:
            sim = v
        else:
            sim = np.vstack((sim, v))
    return sim

#define differential equation of seir model
def seir_eq9(v, t, keys):
    b  = keys['b']
    lp = keys['lp']
    ip = keys['ip']
    f1 = keys['f1']
    k1 = keys['k1']
    k2 = keys['k2']
    #
    s   = v[0];
    e   = v[1];
    i1  = v[2];
    i2  = v[3];
    r   = v[4];
    d   = v[5];
    #
    ds  = - b * s * i1
    de  = - ds     - (1/lp) * e
    di1 = (1/lp)*e - (1/ip) * i1
    di2 =    f1 *d - (1/ip) * i2
    dr  = (1/ip)*(i1 + i2)
    dd  = k1* (k2* di1 + di2)
    return [ds, de, di1, di2, dr, dd]

# case 9.1
def calcsim( S0, keys):
    # solve seir model
    #           S  E I1 I2  R  D
    ini_state=[S0, 0, 1, 0, 0, 0]
    t_max=180
    dt=0.01
    t=np.arange(0,t_max,dt)
    keys['b'] = keys['R0']/(S0*keys['ip'])
    #
    sim = my_odeint(seir_eq9, ini_state, t, keys)
    #
    plt.rcParams["font.size"] = 12
    fig, ax = plt.subplots(figsize=(10,5))
    ax.plot(t,sim[:,[0,1,2,3,4,5]]) # extract E I R1 R2
    ax.set_xticks(np.linspace(0,t_max,19))
    ax.grid(which='both')
    ax.legend([ 'Susceptible','Exposed', 'Infected1(true)', 'Infected2(fake)','Recoverd', 'Detection'])
    ax.set_xlabel('date')
    ax.set_ylim(0,)
    plt.show()
    print("R(tmax):{}".format(sim[-1,4]))
    fig.savefig('m9_1_S0_{}_f1_{}.jpg'.format(S0, keys['f1']))

# try different f1
keys = {'lp':5, 'ip':8, 'R0':2.5, 'k1':10.,'k2':0.2, 'f1':0.0125 }
calcsim(1000, keys)
keys = {'lp':5, 'ip':8, 'R0':2.5, 'k1':10.,'k2':0.2, 'f1':0.0047 }
calcsim(1000, keys)
keys = {'lp':5, 'ip':8, 'R0':2.5, 'k1':10.,'k2':0.2, 'f1':0.0 }
calcsim(1000, keys)

# case 9.2
def calcF1toRfin(S0):
    #           S  E I1 I2  R  D
    ini_state=[S0, 0, 1, 0, 0, 0]
    t_max=180
    dt=0.01
    t=np.arange(0,t_max,dt)
    #
    lp = 5
    ip = 8
    keys = {'lp':5, 'ip':8, 'R0':2.5, 'k1':10.,'k2':0.2, 'f1':0. }
    keys['b'] = keys['R0']/(S0*keys['ip'])
    #
    mklist = lambda e, l : np.append(np.array(e),l)
    #
    rslt = []
    for i in np.linspace(0,0.015,20):
        keys['f1'] = i
        sim = my_odeint(seir_eq9, ini_state, t, keys)
        e1 = keys['k1']*keys['f1']-1./keys['ip']
        r = mklist(keys['f1'], [sim[-1][4], e1])  # (i, R(tmax))
        rslt.append(r)
    #
    rslt = np.array(rslt)
    ymax = max(rslt[:,1])
    plt.rcParams["font.size"] = 12
    fig, ax = plt.subplots(figsize=(10,5))
    #
    ax.plot( rslt[:,0], rslt[:,1], 'b')
    ax.plot( [0, rslt[-1,0]], [S0, S0], 'b:')
    ax2 = ax.twinx()
    ax2.plot( rslt[:,0], rslt[:,2], 'r')
    ax2.plot( [0, rslt[-1,0]], [0, 0], 'r:')
    ax.legend([ 'R(Total infected)'], loc='upper left')
    ax2.legend([ 'eigen value e(A)'], loc='upper center')
    ax.grid(which='both')
    ax.set_xlabel('false positive rate')
    ax.set_ylabel('total infected cases at tmax')
    ax2.set_ylabel('eigen value e(A)')
    #
    ax.set_xlim(0,)
    ax.set_ylim(0,)
    plt.show()
    fig.savefig('m9_2_S0_{}.jpg'.format(S0))
   
calcF1toRfin(1000)