新型コロナウイルス対策としての休業の効果をSEIRモデルで検証

はじめに

　新型コロナウイルス（COVID-19)に対する日本の状況は2020年3月5日現在、諸外国から入国規制がなされるなど、かなり深刻に受け止められています。政府による全国小中高校の一斉休業要請がなされ、一部でその効果が疑問視される声があるものの、一方で、科学的な根拠を示すことが難しいことに政治判断が必要なことも理解できます。
　この記事は、感染症数理モデルの一つであるSEIRモデルを使って、ある学校・事業所（1000人規模とする）を一定期間休業することによる感染のピーク制御が果たして可能なのか検証したものです。
　ただし、この記事はあくまで限定的な仮定のもとでのシミュレーションであり、科学的な確証を与えるものでも、学術的なエビデンスを与えるものでもありません。あくまで、参考になるかもしれないし、間違っているかもしれないものですので、一切の責任は負いかねます。
　なお、大部分のプログラムは[こちらの記事] (https://qiita.com/Student-M/items/4e3e286bf08b7320b665)を参考にさせて頂きました。

前提条件

SEIRモデルの詳細はこの記事では省略しますが、Wikipediaによれば、

• S:感染症に対して免疫を持たない者(Susceptible)
• E:感染症が潜伏期間中の者(Exposed)
• I:発症者(Infectious)
• R:感染症から回復し免疫を獲得した者(Recovered)

から構成され、その頭文字をとってSEIRモデルと呼ばれる。 らしいです。
SEIRモデルのパラメータには、

• β:感染率
• lp:潜伏期間
• ip:感染期間

があります。潜伏期間は厚生労働省によれば、「ＷＨＯの知見によれば、現時点で潜伏期間は1-12.5日（多くは５-６日）とされており、」とありますので仮に5.5日とします。
感染期間は不明ですが、発症して大体４日間発熱が続き、その後回復するか、重症化するかと言われていますので仮に8日とします。（重症化した場合、入院すると考えられますが、軽症者は特に自覚なく普段通りの生活を送りながら回復するものとします。）
最も重要なのが感染率ですが、厚生労働省が出しているデータに基づき以下のようにしました。

感染率

厚生労働省のQ&Aによりますと、一人の感染者が２次感染を引き起こす頻度は下図のようです。

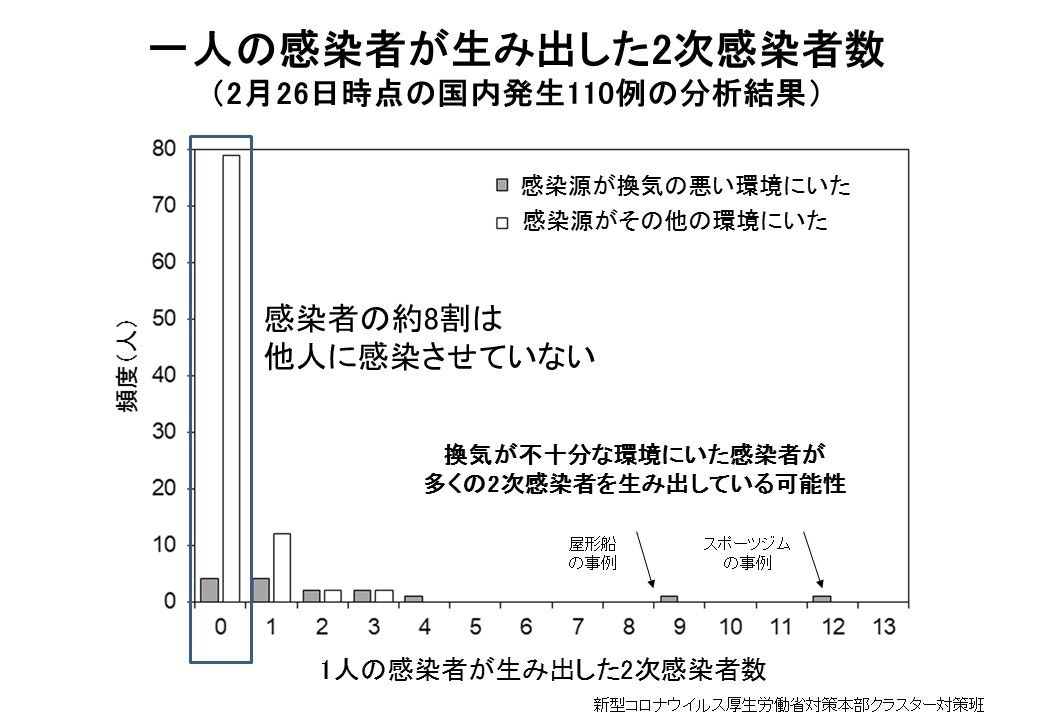
このデータから、一様乱数を使って、
２次感染を生み出す率R0（基本再生産数）を計算する関数を定義します。

def COVID19R0(er):
    if np.random.rand() < er:
        # good environment
        if np.random.rand() < 0.8:
            R0 = 0
        else:
            R0 = np.random.randint(1,4)*1.0
    else:
        # bad environment
        R0 = np.random.randint(0,12)*1.0
    return R0

ここで、erは感染源が換気の悪い環境にいた確率として定義します。

• er: 感染源が換気の悪い環境にいた確率

追加パラメータ

また、休業の影響を評価したいので、次のパラメータを導入します。

• tb:休業開始日
• te:休業終了日

R0やこれらのパラメータに基づいて、SEIRモデルを次のように修正しました。

#define differencial equation of seir model
def seir_eq5(v,t, keys):
    er = keys['er']
    lp = keys['lp']
    ip = keys['ip']
    tb = keys['tb']
    te = keys['te']
    #
    if t >= tb and t <= te: # 休業期間
        R0 = 0 # 完全休業（学校・事業所内に人がいない状態）
    else:
        R0 = COVID19R0(er)
    #
    ds = - R0/ip * v[2] if v[0] >= 0 else 0 # note: s >= 0
    de = -ds - (1/lp) * v[1]
    di = (1/lp)*v[1] - (1/ip)*v[2]
    dr = (1/ip)*v[2]
    return [ds, de, di, dr]

その他のプログラム

シミュレーションを実行するため、ライブラリをインポートします。

import numpy as np
import matplotlib.pyplot as plt

ODEを解くための関数を定義します。

def my_odeint(deq, ini_state, tseq, keys):
    sim = None
    v = np.array(ini_state).astype(np.float64)
    dt = (tseq[1] - tseq[0])*1.0
    for t in tseq:
        dv = deq(v,t, keys)
        v = v + np.array(dv) * dt
        if sim is None:
            sim = v
        else:
            sim = np.vstack((sim, v))
    return sim

計算して、結果をグラフ化するコードです。

#solve seir model
ini_state=[999,0,1,0]
t_max=180
dt=0.01
t=np.arange(0,t_max,dt)
#
keys = {'er':0.5, 'lp':5.5, 'ip':8, 'tb':0, 'te':0}
sim = my_odeint(seir_eq5, ini_state, t, keys)
#
plt.rcParams["font.size"] = 12
fig, ax = plt.subplots(figsize=(10,5))
ax.plot(t,sim)
ax.set_xticks(np.linspace(0,t_max,19))
ax.set_yticks(np.linspace(0,1000,11))
ax.grid(which='both')
ax.legend(['Susceptible','Exposed','Infected','Recovered'])
plt.show()

ここでは、er（感染源が換気の悪い環境にいた確率）は仮に0.5としました。

シミュレーション結果

1000人の事業所のうち、0日目に1人感染者がいる状態からスタートします。

まずは、休業を全くしない場合です。

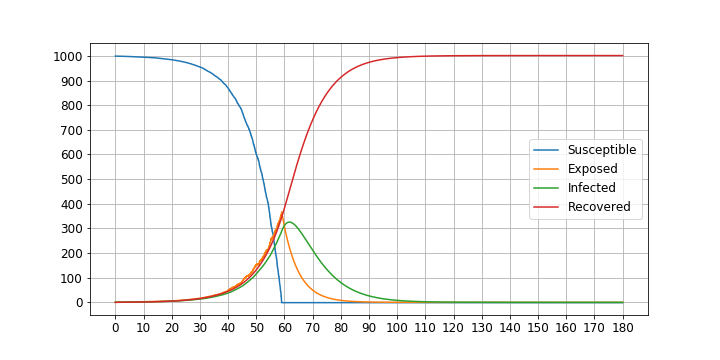
およそ60日目がピークとなり、最大で約320人の感染者がいる日が発生しています。

かなり早い段階（30日目）から20日間休業をした場合です。

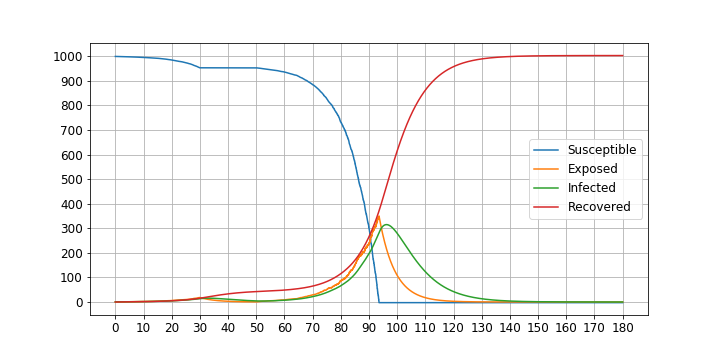
およそ95日目がピークとなり、最大で約310人の感染者がいる日が発生しています。
ピークの遅延日数（35=95-60)が休業期間(20日)よりも長い点は興味深いです。

感染が急速に立ち上がり始めた段階（50日目）から20日間休業をした場合です。

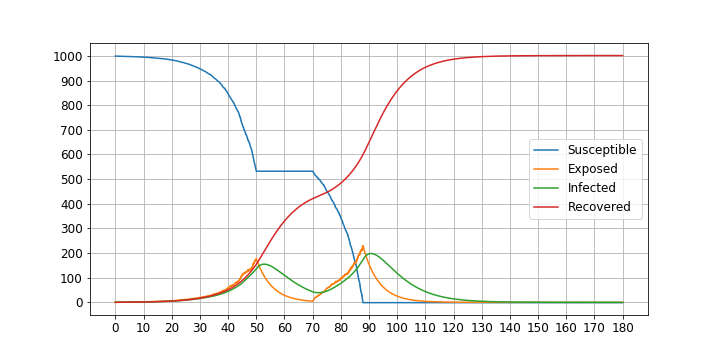
ピークが52日目と90日目に分散され、90日目に最大で約200人の感染者がいる日が発生しています。

感染が収まり始めた段階（60日目）から20日間休業をした場合です。

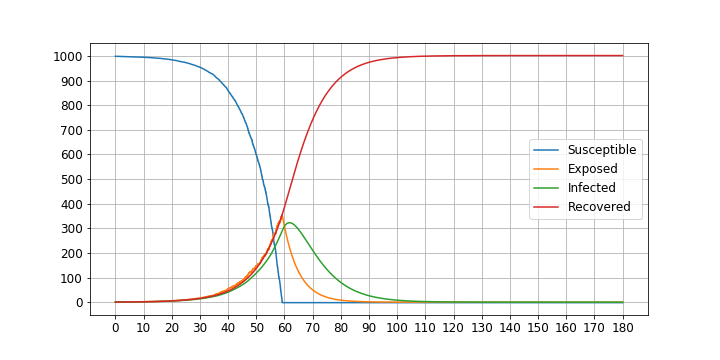
休業を全くしない場合と同じ結果です。これは、60日目には、S:感染症に対して免疫を持たない者(Susceptible)がいなくなったためと考えられます。

考察

以上から、学校・事業所（1000人規模とする）を一定期間（20日間）休業することによる感染のピーク制御に関して、次の傾向がシミュレーションから導けます。

• 感染者がほとんどいない段階で休業した場合、ピークを遅らせる効果は期待できるが、ピーク感染者数はあまり変わらない。
• 感染が急速に立ち上がり始めた段階で休業した場合、ピークが分散される効果と、ピーク感染者数を減らす効果が期待できる。
• 感染が収まり始めた段階で休業しても、効果はない。

したがって、休業をするのであれば、「感染が急速に立ち上がり始めた段階」から「感染が収まり始める前」に行うのが最大の効果が得られるのではないのでしょうか。

さらに言えば・・・

• 1000人中1人でも感染者がいれば、60日程度で感染がピークを迎えるので、厳しい水際対策は、遅延以外あまり効果が期待できないのではないかと思います。
• 2020年の春節は1月24日からなので、日本の感染ピークの目安の一つは3月下旬～4月上旬ではないですかね。
• なので、ピークを迎える10日くらい前、3月20日くらいが対策の正念場ではないかと…。
• SEIRモデル上、感染が完全に収束するのは、R:感染症から回復し免疫を獲得した者が増え切った段階です。したがって、早急なワクチン開発や治療薬の開発が強く望まれます。
• 感染は、S:感染症に対して免疫を持たない者とI:発症者が出会って初めて起こるので、そういう出会いの機会（クラスターの発生しやすい機会）を減らすのは十分意義があると思います。
• 東京都などは、感染の動向をグラフで公表しています。自分の住んでいる自治体がどの感染フェーズにいるのか判断するのに重要ですので、各自治体も同様なデータ公表をして欲しいですね。

参考リンク

下記のページを参考にさせて頂きました。

• 感染症数理モデル事始め　PythonによるSEIRモデルの概要とパラメータ推定入門
• SEIRモデル
• 新型コロナウイルスに関するQ&A（一般の方向け）
• [#新型コロナウイルス 感染拡大防止取り組みの重要性を SIRモデル で検証(2020.2.26作成)] (https://togetter.com/li/1473829)
• 都内の最新感染動向