新型コロナウイルスの実効再生産数の世界動向から収束時期を検討してみる

はじめに

　新型コロナウイルス感染症(COVID-19)に関連して、実効再生産数¹を都道府県別に分析したり、ランキングして来ましたが、今回、世界のデータに目を向けて、実効再生産数の推移から、収束時期が予測できないか検討して見ました。特に、7月に東京オリンピック2020が開催できるかどうかの瀬戸際ですので、日本だけでなく、世界的にも一刻も早い収束が望まれます。
※3/23 データの変動が激しく見にくかったため、移動平均処理を追加しました。
※3/23 プロットのスタイルを変更しました。

結論

　まず、結論から簡潔に述べますと、

1. 欧州では3月21日ころに感染ピークを迎え、実効再生産数が$R \leq 1$となった可能性があるが、それが観測されるのは4月上旬ごろと思われます。
2. 米国、豪州、東南アジア（マレーシア、インドネシア）、中東（トルコ、イスラエル）では、$R$が10付近の高い水準で推移して収束傾向が見られないため、予断を許さない状況。
3. 比較的拡大が抑えられている国（台湾、香港、シンガポール、日本）でも、時折$R$が跳ね上がることがあるため、国外からの流入に注意が必要。

前提

　基本的な計算式は、前回の記事の内容と同一です。パラメータも変えていません。また、データは新型コロナウイルスデータセットを使用させて頂きました。このような公開データを提供されている努力に敬意を表します。
　潜伏期間や感染期間を経て、検査陽性が判明するというタイムラグがあるため、直近2週間以前の結果は出ていません。

Pythonで計算してみる

　今回のコードは、GitHubで公開しています。Jupyter Notebook形式で保存してあります。(ファイル名：03_R0_estimation-WLD-02b.ipynb)

• [GitHub: okimebarun/01_COVID19_analysis] (https://github.com/okimebarun/01_COVID19_analysis)

コード

特に、前回の記事を踏襲しているため、あまり変更点はありません。
強いて言うなら、累積値のデータを日々の確定データに変えるため、差分をとっています。

def readCsvOfWorldArea(area : None):
    # 下記URLよりダウンロード
    # https://hackmd.io/@covid19-kenmo/dataset/https%3A%2F%2Fhackmd.io%2F%40covid19-kenmo%2Fdataset
    fcsv = u'World-COVID-19.csv'
    df = pd.read_csv(fcsv, header=0, encoding='sjis', parse_dates=[u'日付'])
    # 日付, 対象国を抽出
    if area is not None:
        df1 = df.loc[:,[u'日付',area]]
    else:
        df1 = df.loc[:,[u'日付',u'世界全体の感染者']]        
    df1.columns = ['date','Psum']
    ## 累積⇒日次に変換
    df2 = df1.copy()
    df2.columns = ['date','P']
    df2.iloc[0,1] = 0
    ## 文字列⇒数値
    getFloat = lambda e: float('{}'.format(e).replace(',',''))
    ## 差分計算
    for i in range(1,len(df1)):
        df2.iloc[i, 1] = getFloat(df1.iloc[i, 1]) - getFloat(df1.iloc[i-1, 1] )
    ##
    return df2

Rの計算処理に、移動平均を追加しました。前後3日での平均をとっています。

def calcR0(df, keys):
    lp = keys['lp']
    ip = keys['ip']
    nrow = len(df)
    getP = lambda s: df.loc[s, 'P'] if s < nrow else np.NaN
    getP2 = lambda s: np.average([ getP(s + r) for r in range(-1,2)])
    for t in range(1, nrow):
        df.loc[t, 'Ppre'] = sum([ getP2(s) for s in range(t+1, t + ip + 1)])
        df.loc[t, 'Pat' ] = getP2(t + lp + ip)
        if df.loc[t, 'Ppre'] > 0:
            df.loc[t, 'R0'  ] = ip * df.loc[t, 'Pat'] / df.loc[t, 'Ppre']
        else:
            df.loc[t, 'R0'  ] = np.NaN
    return df

また、軸を見やすくするため、対数軸で表示しています。

def showResult3(dflist, title):
    # R0=1
    dfs = dflist[0][0]
    ptgt = pd.DataFrame([[dfs.iloc[0,0],1],[dfs.iloc[len(dfs)-1,0],1]])
    ptgt.columns = ['date','target']
    ax = ptgt.plot(title='COVID-19 R0', x='date',y='target',style='r--', figsize=(10,8))
    ax.set_yscale("symlog", linthreshy=1)
    #
    for df, label in dflist:
        showResult2(ax, df, label)
    #
    ax.grid(True)
    ax.set_ylim(0,)
    plt.show()
    fig = ax.get_figure()
    fig.savefig("R0_{}.png".format(title))

元のコードをあまり変えずに対応できたので、助かりました。

計算結果

それでは、いよいよ計算結果を見てみましょう。$R_0 >1$であれば感染拡大傾向、$R_0<1$であれば感染収束傾向、と言えるでしょう。

爆発的感染が観測された地域

中国本土、イタリア、米国、スペイン、イラン、韓国の結果がこちらです。

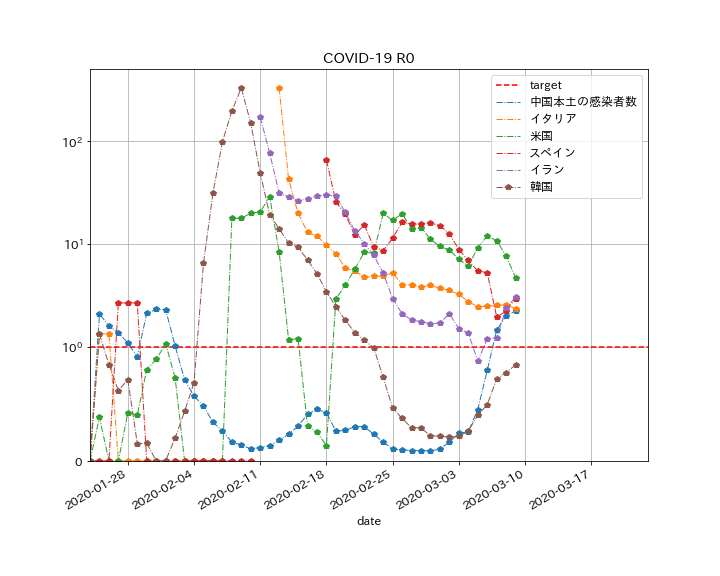
• グラフの形状として、一気にRが増加したあと、段々と漸減していく傾向があるようです。
• アメリカだけ、やや特異な形状に見えます。
• 中国本土と韓国はほぼ収まっている印象です。

ヨーロッパ

イタリアをはじめ、ヨーロッパでも感染者の多い国を集めた結果がこちらです。

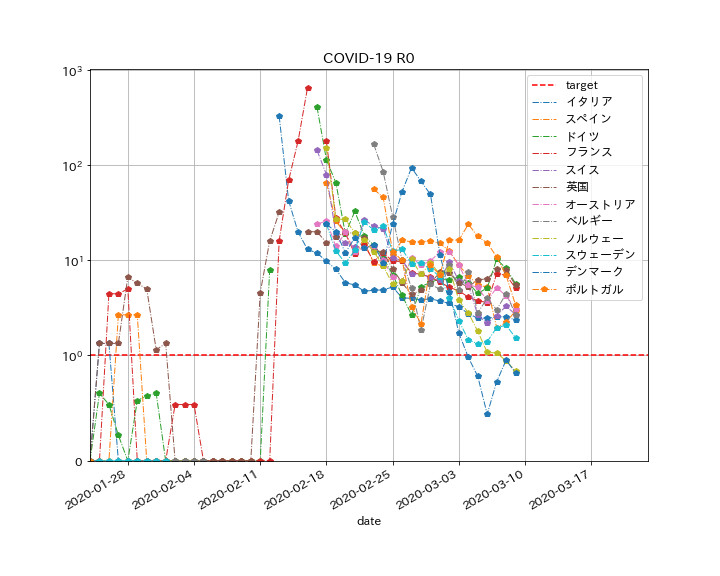
• デンマークは2月25日付近までは漸減傾向にあったものの、2月26日～3月1日あたりに一気にぶり返しています。
• 最近はイタリアの代わりにスペインが$R$のトップに置き換わっているようです。
• その他のヨーロッパ諸国の傾向はかなり似ています。

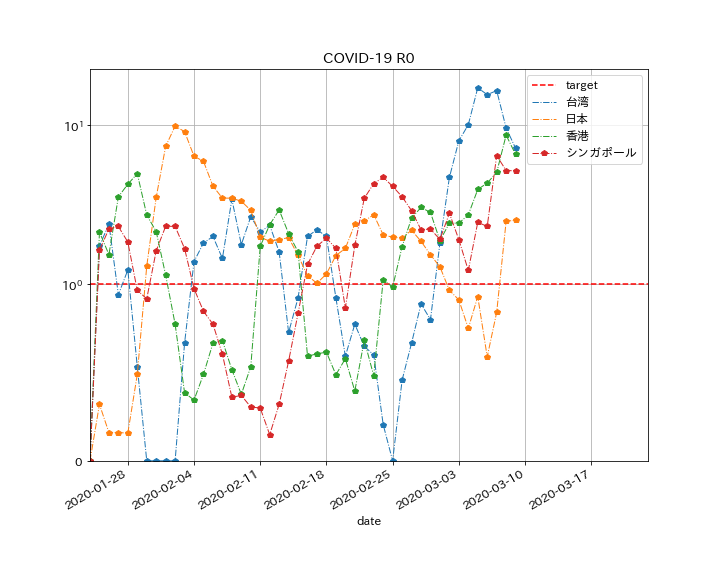
アジア周辺で比較的感染が抑制されている地域

台湾、日本、香港、シンガポールの結果がこちらです。

• 台湾、香港、シンガポールは1を切ることも多く、よく抑えられているようですが、3月に入ってピークが見られ、海外からの流入が懸念されます。
• 日本は、シンガポールと香港あたりによく似ています。ここから、継続的に1を割っていければ収束が見えてきます。

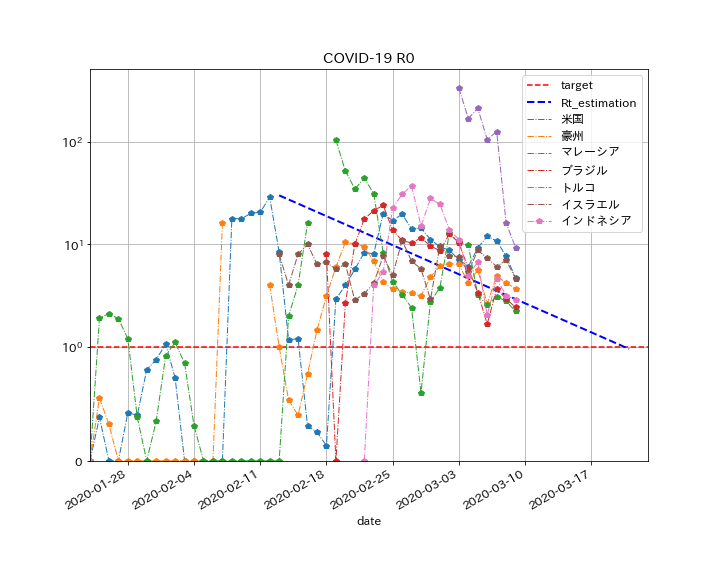
今後感染拡大が懸念される地域

全てではありませんが、グラフを見ながら、$R$が高い水準で推移しており、収束傾向が見られない国を集めた結果がこちらです。

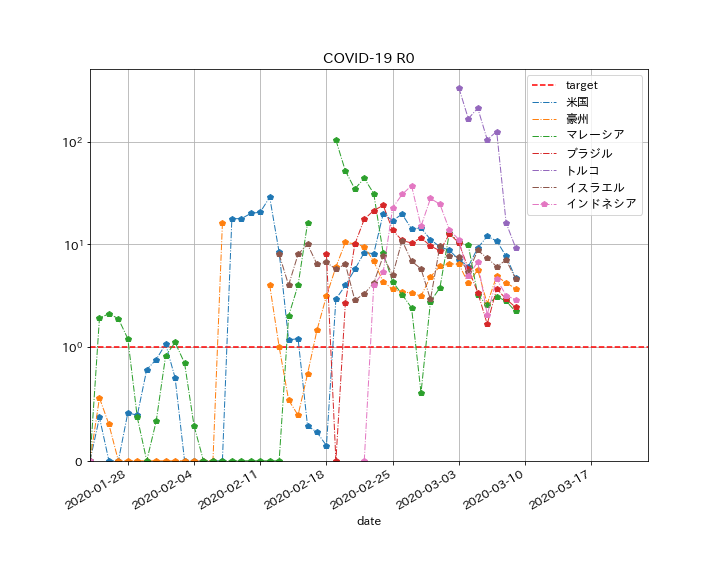
• 3月22日現在、感染者の比較的多い国で、$R$の収束傾向が確認できない国です。
• おおむね$R=10$付近で推移しており、ヨーロッパのように漸減していないように見えます。
• 共通点は、良くわかりません((+_+))。

ヨーロッパの結果をもとに、実効再生産数の近似式を引いてみる

　実効再生産数の推移を見ますと、急激に上がったあとは、指数的に漸減していく傾向が見られます。特に、ヨーロッパの結果を見ますと、国によらず同じような収束傾向が見られます。そこで、以下の近似式で当てはめてみました。

R(t) = R(t_0) \cdot 2^{-\frac{t-t_0}{T}}

つまり、$R(t)$の半減期が$T$である、というモデルです。
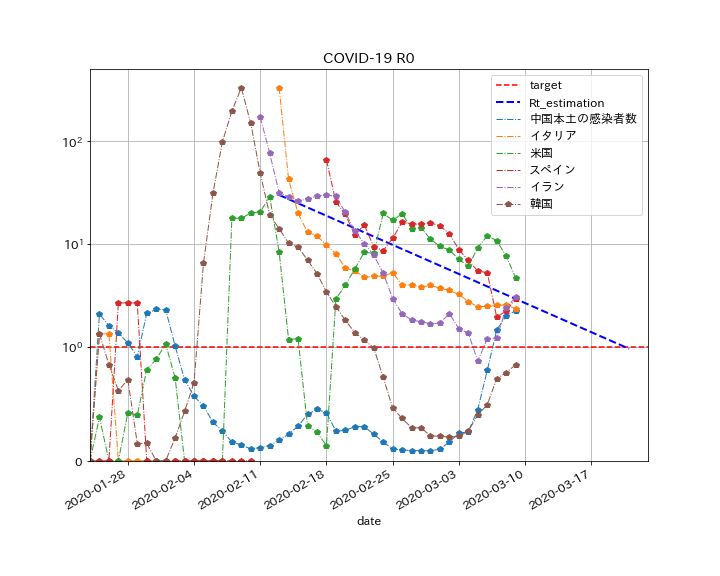
　実際、$T=7.5[days]$として、ヨーロッパ地域のグラフに合わせてみると、以下のようになります（図中の点線が推定式）。

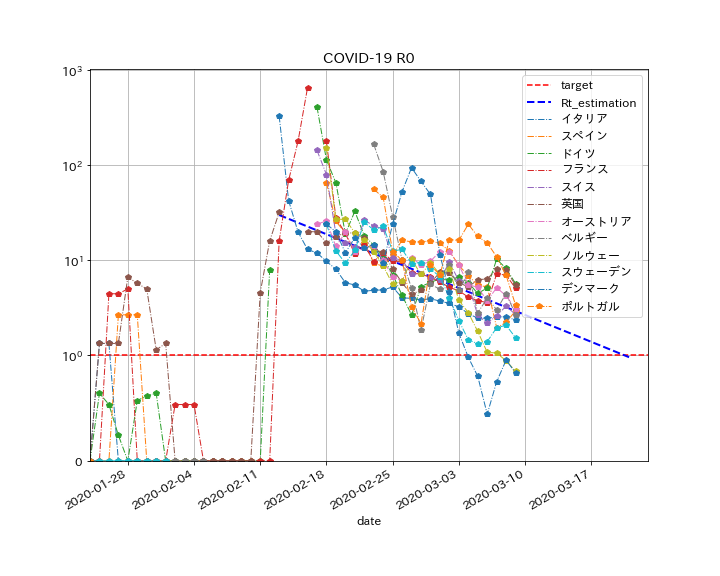
　ここから、具体的に$R(t)$に日付を代入してみると、

• 2020-03-01に、$R(t)=6.23$
• 2020-03-21に、$R(t)=0.98$
• 2020-04-15に、$R(t)=0.097$
• 2020-04-30に、$R(t)=0.024$
• 2020-05-15に、$R(t)=0.0061$

という結果になります。もちろん、近似ですので、この通りにならない可能性があります。しかし、直近の3月21日に$R<1$になっているとすれば、新規感染者の増加が一定に収まっているという傾向が、13日後の4月4日ごろに観測されるはずです。そうであれば、入院患者数がどんどん減っていき収束が見えてくるのではないでしょうか。

また、上記の近似式を他地域にも当てはめて見た結果がこちらです。

爆発的感染が観測された地域

今後感染拡大が懸念される地域

さらに言えば・・・

• 3月22日現在、南米地域はエクアドルの532名、アフリカ地域はエジプトの294名が最多のようですが、今後増加していく可能性があり、注視していく必要があるでしょう。
• 今後感染拡大が懸念される地域、特にアメリカの動向が心配です。ワシントン州、ニューヨーク州、カリフォルニア州などで非常事態宣言がなされ、ロックダウンも始まっているようですが、まだ、$R$の減少傾向は数字に現れていません。
• 当然、日本も引き続き警戒をしていく必要があります。

参考リンク

下記のページを参考にさせて頂きました。

1. 新型コロナウイルスデータセット
2. 「新型コロナウイルス感染症対策の状況分析・提言」（2020年3月19日）
3. 新型コロナウイルスの都道府県別の基本再生産数の推移を計算してみる
4. 新型コロナウイルスの都道府県別の効果的再生産数のランキングを出してみる

1. 本記事では、（ある時刻tにおける，一定の対策下での）1人の感染者による2次感染者数と定義します。 ↩