はじめに
新型コロナウイルス感染症(COVID-19)は、感染の場を中国から欧州、米州へと広げ猛威を振るっています。日本においても、3月27日現在、国内での感染者は1254名で、東京都においても週末の外出自粛規制を都知事が要請する事態となっています。しかしながら、医療が比較的整っていると思われるG7各国と比較しても、アメリカ85594名、イタリア80589名、ドイツ43938名、フランス9155名、イギリス11658名、カナダ4043名と、日本の少なさが際立っています。
本記事では、この理由を説明する一つの仮説として、クラスター対策に注目した数理モデルで説明できないかを検討しました。検討の流れとして、従来モデルの問題点、新しいモデルの検討、シミュレーション、考察、となっています。
結論
まず、結論から述べますと、
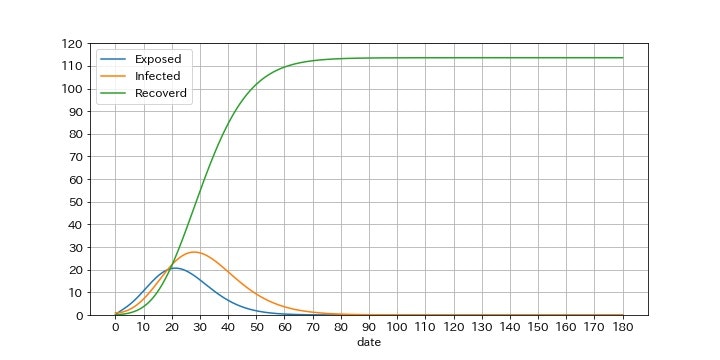
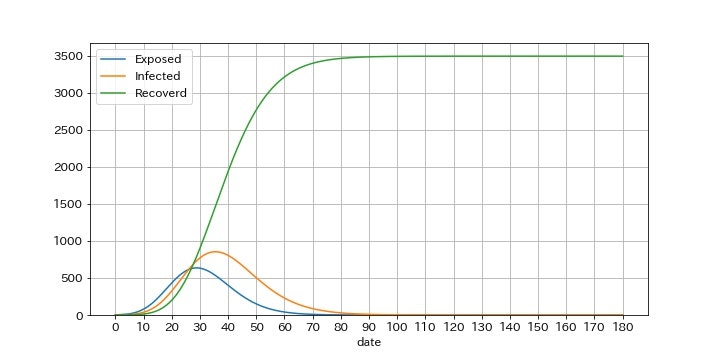
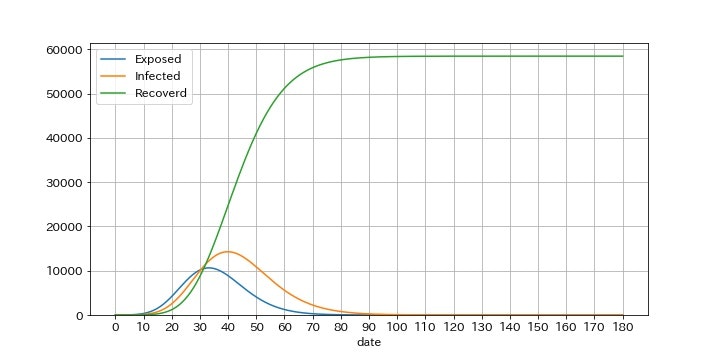
- クラスターの発生を放置すると爆発的に総感染者数は増加し、初期再生産数10のクラスターが113人、初期再生産数20のクラスターが3493人、初期再生産数30のクラスターが58437人、の感染者を生み出す。
- クラスター対策の効果は、早ければ早いほど、クラスター規模が大きければ大きいほど効果が期待でき、クラスター発生時から20日までに隔離できれば総感染者数を半減以上できる可能性がある。
- ただし、 クラスター発生時から50日経過してしまうと、クラスター対策の効果はほとんど消えてしまう。
- なので、ルートの追えない感染者が増加してる場合、一律の外出禁止を早期に行うことが合理的。
- 欧米G7各国と日本との違いの要因は、早期にクラスター対策に動いたこと、大規模イベント自粛により初期生産数の多いクラスターを抑止したこと、に加え、宗教的な施設での集会が少ないこと、などが考えられる。
従来モデル(SEIRモデル)の限界
下記の記事で、SEIRモデルと呼ばれる感染症の推移を計算するモデルを使って計算してきました。
SEIRモデルは簡単に言うと、S:感染症に対して免疫を持たない者(Susceptible)、E:感染症が潜伏期間中の者(Exposed)、I:発症者(Infectious)、R:感染症から回復し免疫を獲得した者(Recovered)の4者の間で、ある集団の分布がどのように推移していくのかを微分方程式で表したモデルです。
感染症の動向分析でよく使われているようで、日本の厚生省やイギリスの保健省、アメリカCDCの説明資料などでも度々出てきます。
しかしながら、人口集団Sを国全体や県全体など大きな集団を基準に計算しようとすると全く桁が合いません。例えば、上記の記事で検討したSEIRモデルの計算では、1000人の集団を仮定すると、60日でピークを迎え、ピーク時は人口の30%以上が感染者になってしまいますが、人口比での感染者数が非常に多いイタリアを見ても、現在の感染者数は人口6048万人の0.1%程度に過ぎません。
理由は様々考えられますが、例えば以下のようなことが想定されます。
- (未感染者数)Sに比例して再生産数が増加するという仮定に無理がある。
- 地域の地理的要因・交通要因を考慮していない。例えば、沖縄の感染者が北海道に感染をすぐ広げるとは考えにくいですよね?
- 個人の行動範囲を考慮していない。例えば、ずっと家にいる人と、しょっちゅう色んな人と接する人とではパラメータが違ってくるはずです。
そこで、実際に観測されたデータから、もっと事実を説明できるモデルが出来ないかを考えてみます。
クラスター基準SEIRモデルを考える
そこで、実際に観測された現象を確認してみましょう。下の図は、新型コロナウイルスの実効再生産数の世界動向から収束時期を検討してみるで計算した結果です。
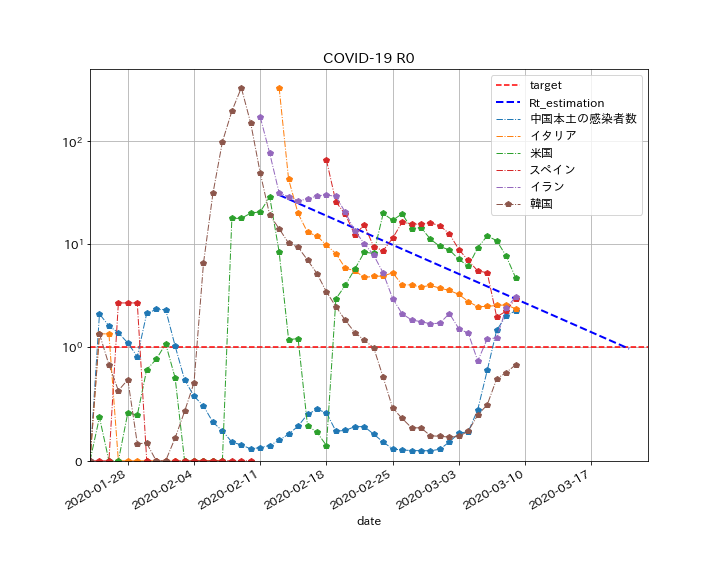
グラフの数値は、実効基本再生産数(以下、Rpと呼ぶことにします。)をある基準で計算したものです。点線はグラフを近似した近似式(対数線形)です。このグラフから読み取れる傾向は次の通りです。
- 初期にRpが爆発的(>100)に増大し、その後対数線形の傾きを持ちながら段々と漸減していく。
なので、素直にこの観測された傾向をモデル化してしまいましょう。具体的には、
- ある時刻t0でクラスターが発生し、Rp(t0)となる。
- 時刻t0以降の実効再生産数Rp(t)は、一定の対数線形で漸減する。
数式で書くとこうなります。
Rp(t) = Rp(t_0) \cdot 2^{-\frac{t-t_0}{T_h}}, T_h=7.5[days]
この実効再生産数Rp(t)をSEIRモデルに組み込んで、クラスター基準SEIRモデルとします。
\begin{eqnarray}
\frac{dRp}{dt} &=& - \frac{ln2}{T_h}Rp \\
\frac{dS}{dt} &=& -\frac{1}{ip} Rp \cdot I \\
\frac{dE}{dt} &=& -\frac{dS}{dt} - \frac{1}{lp} E \\
\frac{dI}{dt} &=& \frac{1}{lp} E - \frac{1}{ip} I \\
\frac{dR}{dt} &=& \frac{1}{ip} I
\end{eqnarray}
ポイントは、元のSEIRモデルとは異なり、S(t)の初期値には依存しない点です。
以降では、このモデルに、クラスター対策効果、すなわち、クラスターを発見してクラスターを起点とする感染者を発見し隔離する効果を検証してみたいと思います。
Pythonで計算してみる
上記のクラスター基準SEIRモデルをPythonで計算してみましょう。
ライブラリをインポートします。
import numpy as np
import matplotlib.pyplot as plt
ODEを定義します。ここで、クラスター対策の効果を計算するため、ある時刻$T_c$以降では、$Rp=0$で計算します。
#define differencial equation of seir model
def seir_eq7(v, t, keys):
Th = keys['Th']
lp = keys['lp']
ip = keys['ip']
Tc = keys['Tc']
#
Rp = v[0];
s = v[1];
e = v[2];
i = v[3];
r = v[4];
#
if t >= Tc:
Rp = 0
#
dRp = - np.log(2)/Th * Rp
ds = - Rp/ip * i
de = - ds - (1/lp) * e
di = (1/lp)*e - (1/ip)*i
dr = (1/ip)*i
return [dRp, ds, de, di, dr]
ODEを解くための関数を定義します。
def my_odeint(deq, ini_state, tseq, keys):
sim = None
v = np.array(ini_state).astype(np.float64)
dt = (tseq[1] - tseq[0])*1.0
for t in tseq:
dv = deq(v,t, keys)
v = v + np.array(dv) * dt
if sim is None:
sim = v
else:
sim = np.vstack((sim, v))
return sim
クラスター初期値$Rp(t_0)$を色々と変えてシミュレーションするコードです。パラメータは、$lp=5, ip=8, Th=7.5$としています。
# case 7.1
def calcsim(Rp0, keys):
# solve seir model
# Rp S E I R
ini_state=[Rp0, 0, 0, 1, 0]
t_max=180
dt=0.01
t=np.arange(0,t_max,dt)
#
sim = my_odeint(seir_eq7, ini_state, t, keys)
#
plt.rcParams["font.size"] = 12
fig, ax = plt.subplots(figsize=(10,5))
ax.plot(t,sim[:,[2,3,4]]) # extract Rp, E I R
ax.set_xticks(np.linspace(0,t_max,19))
ax.grid(which='both')
ax.legend([ 'Exposed', 'Infected','Recoverd'])
ax.set_xlabel('date')
ax.set_ylim(0,)
plt.show()
print("R(tmax):{}".format(sim[-1,4]))
# try different Rp0
keys = {'lp':5, 'ip':8, 'Th':7.5, 'Tc':200 }
calcsim(100, keys)
calcsim(30, keys)
calcsim(20, keys)
calcsim(10, keys)
# try different Tc
keys = {'lp':5, 'ip':8, 'Th':7.5, 'Tc':20 }
calcsim(10, keys)
keys = {'lp':5, 'ip':8, 'Th':7.5, 'Tc':10 }
calcsim(10, keys)
クラスター対策時刻$T_c$を色々と変えてシミュレーションするコードです。
# case 7.2
def calcTctoRp(Rp0):
# Rp S E I R
ini_state=[Rp0, 0, 0, 1, 0]
t_max=180
dt=0.01
t=np.arange(0,t_max,dt)
#
lp = 5
ip = 8
keys = {'lp':lp, 'ip':ip, 'Th':7.5, 'Tc':(5+0) }
#
rslt = []
for i in range(0,60):
keys['Tc'] = lp + i
sim = my_odeint(seir_eq7, ini_state, t, keys)
rslt.append([keys['Tc'], sim[-1:,4]]) # (i, R(tmax))
#
rslt = np.array(rslt)
ymax = max(rslt[:,1])
plt.rcParams["font.size"] = 12
fig, ax = plt.subplots(figsize=(10,5))
#
ax.plot([0 , 0],[0,ymax],'m:')
ax.plot([lp,lp],[0,ymax],'b:')
ax.plot([lp+ip,lp+ip],[0,ymax],'g:')
#
ax.plot( rslt[:,0], rslt[:,1], 'r')
ax.legend([ '0 day', 'lp days','lp + ip days','Total infected'], loc='lower right')
ax.grid(which='both')
ax.set_xlabel('cluster shutdown date since cluster occured')
ax.set_ylabel('R(tmax)')
#
for tat in [10,13,20,30,40]:
idx = [i for i in range(len(rslt[:,0])) if rslt[i,0] >= tat][0]
print("R_fin with Tc:{} is {}".format(rslt[idx,0], rslt[idx,1]))
#
ax.set_xlim(-1,)
ax.set_ylim(0,)
plt.show()
calcTctoRp(100)
calcTctoRp(30)
calcTctoRp(20)
calcTctoRp(10)
シミュレーション結果
それでは、計算結果を見てみましょう。
初期再生産数$Rp(t_0)$を何パターンか変えた結果、$Rp(t_0)$を固定してクラスター対策時刻$T_c$を何パターンか変えた結果、を示します。
1. 初期再生産数Rp(t_0)の影響
初期再生産数Rp(t_0)=10のとき
初期再生産数Rp(t_0)=20のとき
初期再生産数Rp(t_0)=30のとき
2. クラスター対策時刻Tcの影響
初期再生産数Rp(t_0)=10のときに、クラスター対策時刻Tcを変えて検証します。当然、クラスター対策が早ければ早いほど効果が期待されます。上記のシミュレーションでは、クラスター対策をしない場合、最終的に113人が感染しました。
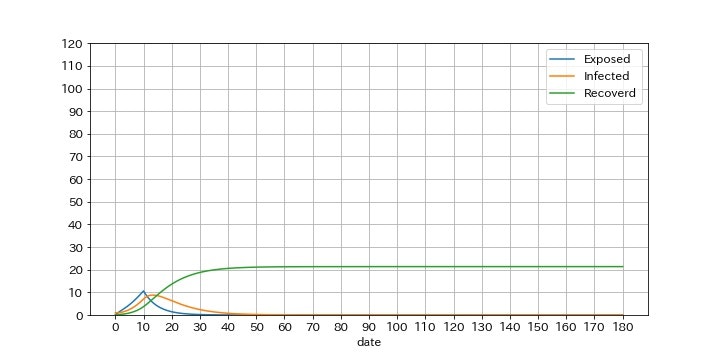
クラスター対策時刻Tc=10[days]のとき
クラスター発生時から10日以内に感染者を隔離できた場合、最終的な感染者は、113人から21人へと減らすことができます。
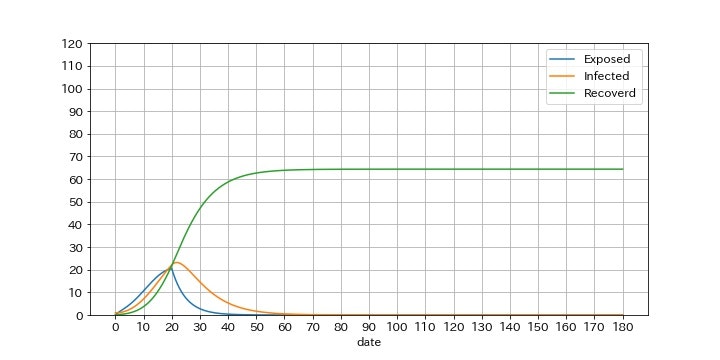
クラスター対策時刻Tc=20[days]のとき
クラスター発生時から20日以内に感染者を隔離できた場合、最終的な感染者は、113人から64人へと減らすことができます。
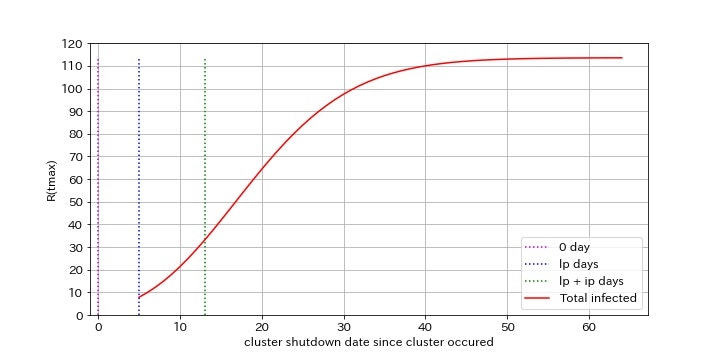
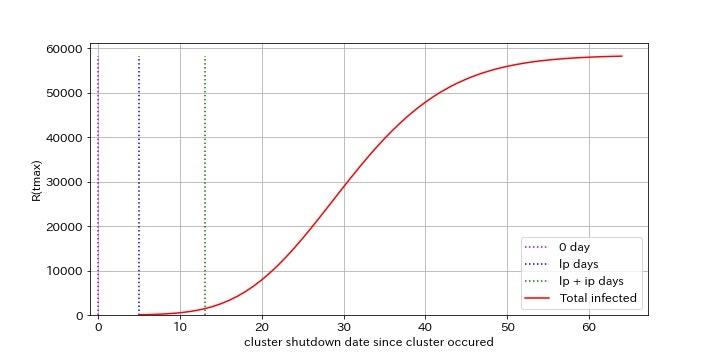
3. クラスター対策時刻Tcと最終的な感染者数の関係
クラスター対策時刻Tcと最終的な感染者数の関係をグラフ化してみます。クラスター発生時、潜伏期間lp経過時、潜伏期間+感染期間(lp+ip)経過時、の3つの時点で点線を引いています。
初期再生産数Rp(t_0)=10のとき
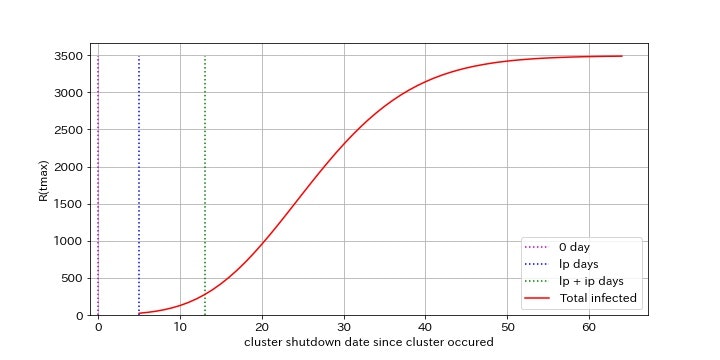
初期再生産数Rp(t_0)=20のとき
Rp(t_0)=10のときと比べて、クラスター対策の効果が相対的に増加しています。
初期再生産数Rp(t_0)=30のとき
Rp(t_0)=20のときと比べて、クラスター対策の効果が相対的に増加しています。
考察
以上から、クラスター基準のSEIRモデルに基づく、感染者数の推移とクラスター対策時刻の効果に関して、次の傾向がシミュレーションから導けます。
- Sの初期値を仮定しないクラスター基準SEIRモデルでも、通常のSEIRモデルとほぼ同形状のカーブとなる。
- クラスターの初期再生産数Rp(t_0)と最終的な感染者数の関係は線形ではなく、初期再生産数Rp(t_0)が多いと最終的な感染者数は爆発的に増大する。
- クラスター対策時刻Tcは早ければ早いほど効果があり、クラスターの初期再生産数Rp(t_0)が多ければ多いほど効果がある。クラスター発生時から20日経過するまでに対策するだけで、最終的な感染者数を半減以上する効果が期待できる。
さらに言えば・・・
- 初期再生産数Rp(t_0)が大きいクラスターを作らないことが極めて重要であることが分かります。
- クラスターの発生を早期に探知して、早めに対処すればするほど、効果は大きく期待できます。大きなクラスターであれば、多少時間がかかっても(発生から20~30日程度)クラスター対策を諦めない方が良いでしょう。
- 欧米G7各国と日本との違いの要因は、早期にクラスター対策に動いたこと、大規模イベント自粛により初期生産数の多いクラスターを抑止したこと、に加え、宗教的な施設での集会が少ないこと、などが考えられます。
- 実際、韓国の大邱市の宗教施設やイランのモスク、日本でもライブハウスなど3密要件を満たす場合はクラスターが発生しました。
- 今、日本でもリンクの追えない感染者の増加が懸念されていますが、それが隠れクラスターによるものである場合、早期の外出禁止により一律に抑制できる可能性はあります。
- ただし、クラスター発生時から50日程度経過してしまうと、ロックダウンをしても効果は期待できません。イタリアやニューヨークで起こっていることがこれである可能性も否定できません…。
参考リンク
下記のページを参考にさせて頂きました。