はじめに

Pycaretとは数行のコードで機械学習モデルを構築・比較してくれるAutoMLライブラリです。

この投稿では以下の状況を取り扱い、結果の解釈やコードの詳細を説明します。

回帰問題
予測モデル作成後、自らが作ったデータセットにモデルを当てはめて予測値を得る

0. データの読込みと前処理

# ライブラリのインポート
# 不要な警告文を非表示にする
import warnings
warnings.filterwarnings("ignore")
from pycaret.regression import *
import pandas as pd

# pycaretのバージョンを確認
import pycaret
print("pycaret version: ", pycaret.__version__)

出力

pycaret version:  3.0.4

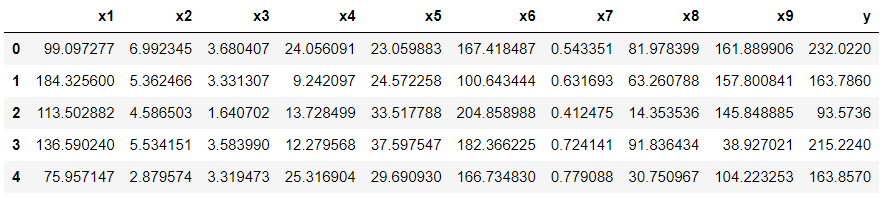
今回はこちらのページで紹介した"df.csv"というデータを用いて予測モデルを組んでいきます。csvファイルはGitHubにも保存しております。

# データの読み込み
df = pd.read_csv("df.csv")
print("Datasize: " + str(df.shape))
df.head()

出力

Datasize: (707, 10)

次にデータの前処理を行っていきます。今回はx2とx3を無視して、x1,x4～x9を説明変数としてyを予測していくことにします。

# データの前処理
reg = setup(df, target ="y", fold = 5, 
            ignore_features = ["x2", "x3"],
            fold_shuffle=True, session_id = 123)

データの型を変更しない場合はEnterを押します。変更が必要な場合は、"quit"と入力し"Enter"を押して分析条件を変更します。

オプション

解析に用いるデータセット（第一引数）
target：目的変数の指定
ignore_features：解析から無視する列を指定
numeric_features：Categoricalではなく、数値データとして読み込んで欲しい列を明示
session_id：random_stateのようなもので再現性を担保、fold_shuffle=Trueとセットで用いる

参考サイト（引数の参考）

1. モデルの比較

この段階ではハイパーパラメータの最適化までは実行されていない。

# 各種モデルの比較
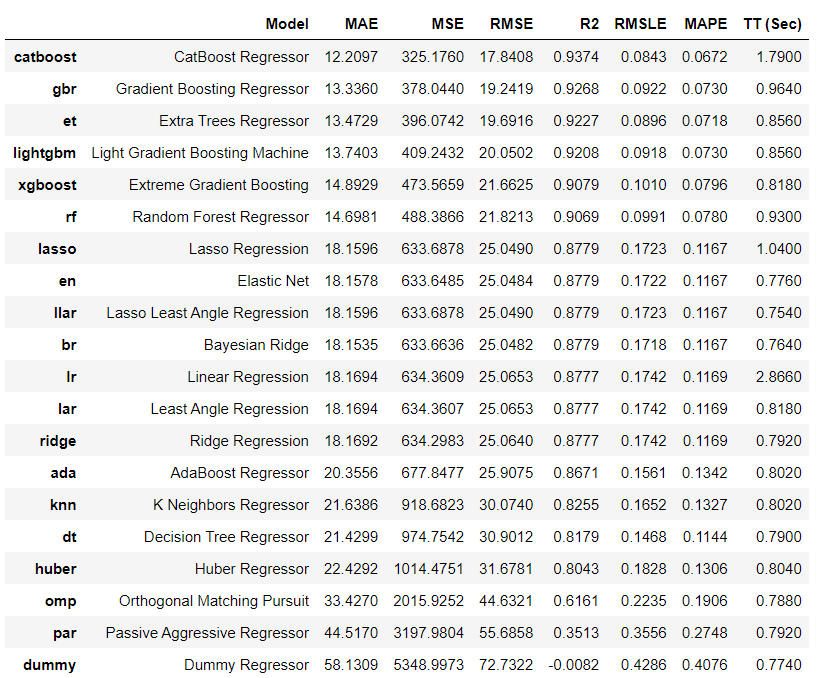
best_model = compare_models()
best_model

2. モデルの確認

確認するモデル名を指定します。ここでは"Light Gradient Boosting Machine"を選択します。

# create_modelの引数に上記で最適化したモデル名を記載
model = create_model('lightgbm')

k-foldした検証結果の詳細が表示される。このMeanの値が上記のモデル比較のスコアとなっている。

3. ハイパーパラメータの最適化

選択したモデルのハイパーパラメータの最適化を行います。ここで決定したハイパーパラメータに基づいて以降の分析が行われていると考えられます。

# ハイパーパラメータの最適化を行う
final_model = tune_model(model, n_iter = 500, optimize = 'r2')

モデルのチューニングが上手くいっていれば、R2などのスコアが上がる。
次に最適化したモデルで結果を可視化していく（公式： https://pycaret.readthedocs.io/en/latest/api/regression.html)

4. モデルのハイパーパラメータの確認

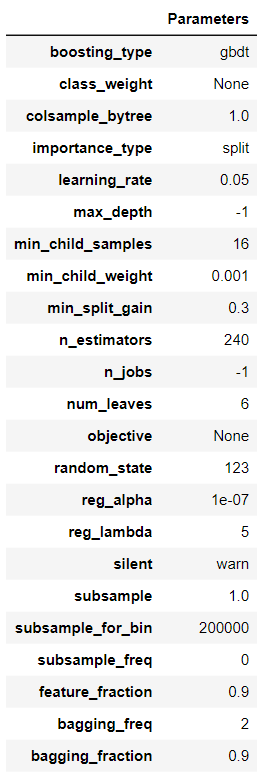
plot_model(final_model, plot = 'parameter')

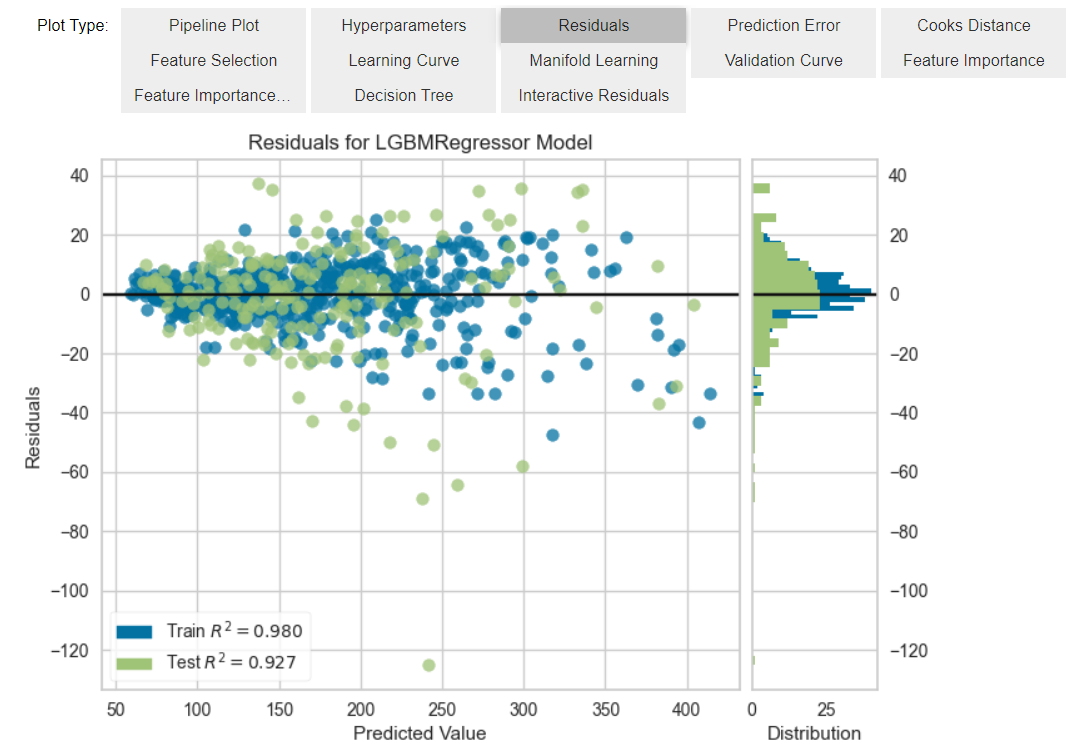
5. 残差プロット

# 可視化　残渣プロット（デフォルトなので引数は指定なしでよい）
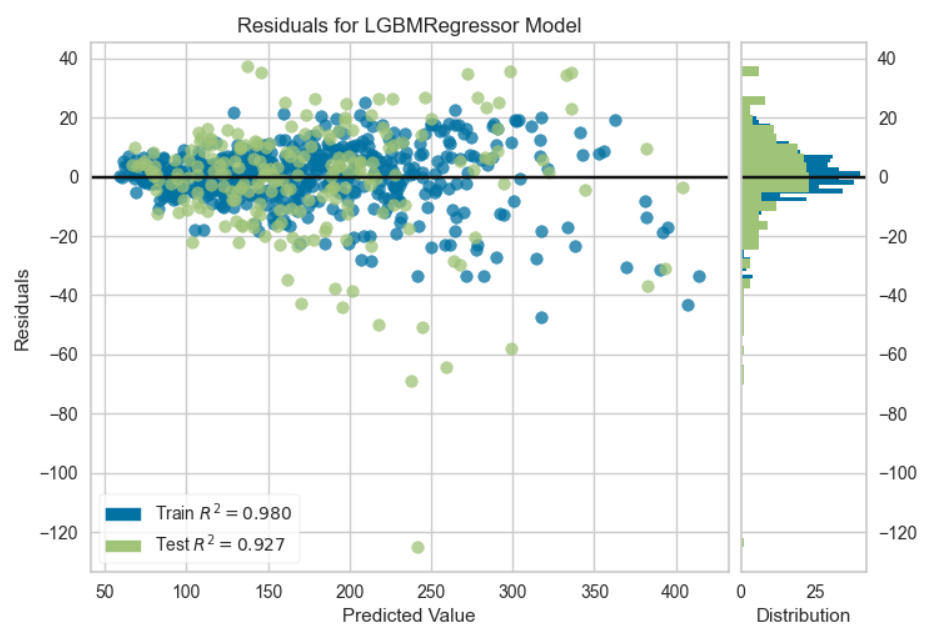
plot_model(final_model)

残差プロットは横軸に予測値、縦軸に残差をプロットする。良い予測モデルであれば、残差0のところにデータが横に並ぶようなプロットになる。予測値の値によって残差に傾向がある場合（例えば予測値が小さい領域では残差が小さいが、予測値が大きい領域では残差が大きい場合はデータの非線形性などが考えられる）残差はランダムな誤差になるはずなので、ヒストグラムは正規分布になる。逆に正規分布にならない場合は、外れ値があることを示唆している。

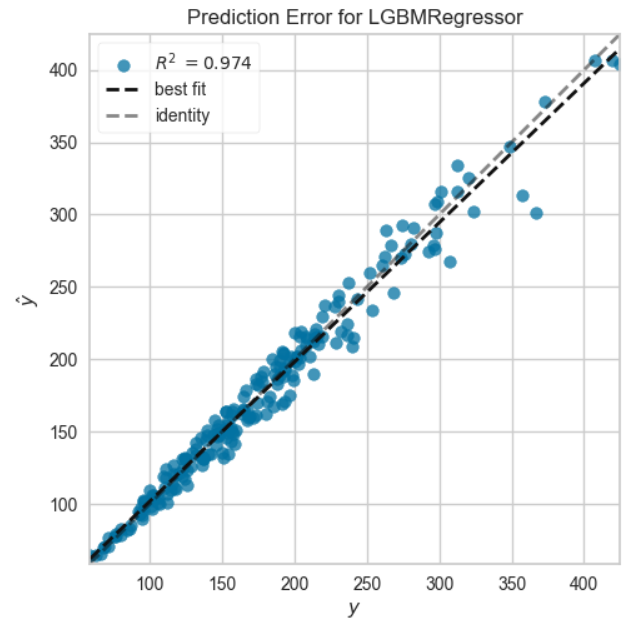
6. 予測誤差プロット

# 可視化　引数plot = error　で誤差プロット
plot_model(final_model, plot = 'error')

テストデータに対する予測誤差（y-y）プロット。横軸に実際の値を、縦軸に予測値をプロットしたもの。予測が完全であれば、傾き1の直線上に点が乗り、点が傾き1の直線周辺に集まるモデルが良いモデルとなる。

7. クックの距離のプロット

# 可視化　引数plot　cooks　でCookの距離プロット（外れ値をみる）
plot_model(final_model, plot = 'cooks')

クックの距離のプロット。クックの距離とは、「i番目の観測値を使用して計算された係数と、観測値を使用しないで計算された係数との間の距離に対する測度」である。Cook の距離が大きいとそのデータが回帰式による予測値に大きく影響していることを意味する。よって、Cook の距離が大きいデータは異常値である可能性がある。図中の破線が、推奨される閾値である。これ以上は「外れ値の可能性あり」と判断できる。

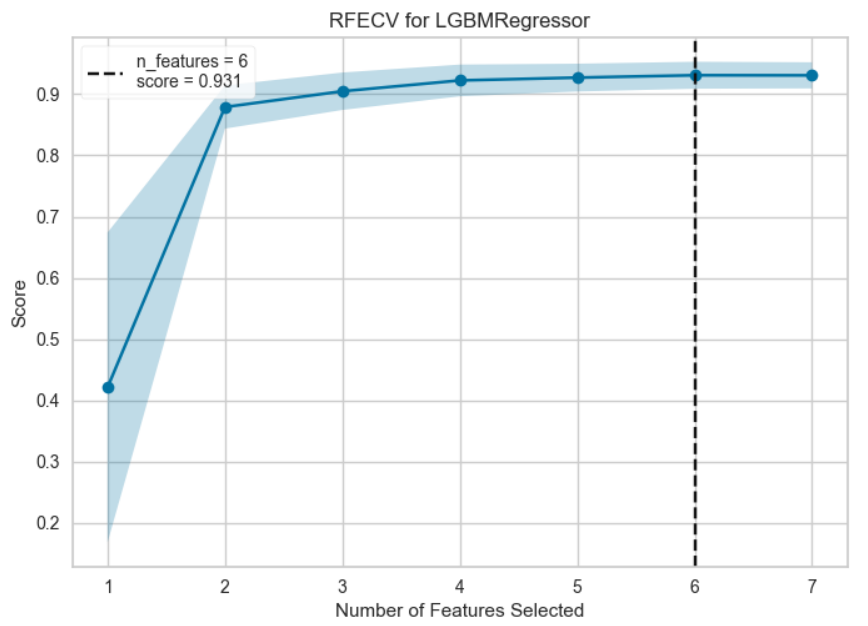
8. 特徴量の選択

# 可視化　引数plot = feature　で特徴重要度プロット
plot_model(final_model, plot = 'rfe')

モデルに使う特徴量の数とモデルのスコアの関係を表している。黒の点線で示す特徴量数でモデルのスコアが最大となる。特徴量はのちで計算するFeature Importanceに基づいて順位が高いものから選択される。

9. 学習曲線

# 可視化　引数plot = learning　で　学習曲線
plot_model(final_model, plot = 'learning')

横軸に訓練データのデータ数、縦軸に予測精度をプロットしている。理想的なモデルではサンプルサイズを大きくした時にTrainig Scoreが下がり、CV Scoreが上がっていき、両者が漸近する。漸近する値があらかじめ設定した値よりも大きいとモデルが上手く作られていると考えられる。両者ともにスコアが低い場合は学習不足なのでパラメータを増やす、学習データのスコアだけが高い場合は過学習気味なのでパラメータ数を減らすなどの対策が必要である。

10. 多様体学習

# 可視化　引数plot = manifold　で　次元削減を行い、特徴を２次現に射影
plot_model(final_model, plot = 'manifold')

t-SNE(t-Distributed Stochastic Neighbor Embedding：t分布型確率的近傍埋め込み法）によって高次元データを2次元に落としてプロットしたグラフ。ここで上手く傾向が見えるようであれば次元削減を行ってモデル解釈性を上げることも可能である。

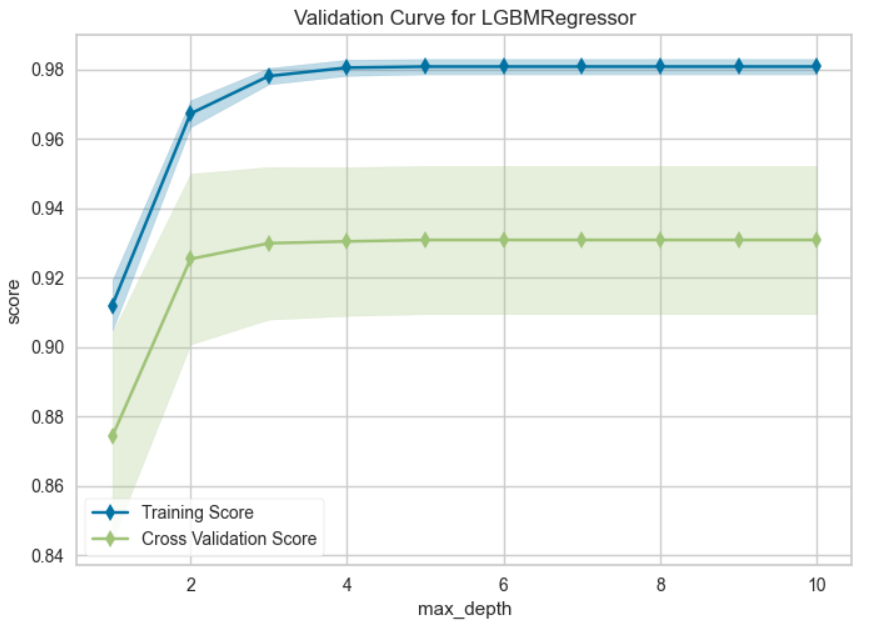
11. 検証曲線

# 可視化　引数plot = vc　で 検証曲線
plot_model(final_model, plot = 'vc')

検証曲線は横軸にハイパーパラメータ、縦軸に予測精度をプロットしている。適切なハイパーパラメータ（例：max_depth：木の深さ）の値はどこかを確認でき、訓練精度と検証制度の差が小さく、精度が高いものを選ぶようにする。（学習不足や過学習を確認することができます。）横軸のハイパーパラメータはアルゴリズムによって異なる。

12. 特徴量の重要度

# 可視化　引数plot = feature　で特徴重要度プロット
plot_model(final_model, plot = 'feature')

説明変数が多い場合は以下のコードで全ての特徴量の重要度が算出可能です。

plot_model(final_model, plot = 'feature_all')

13. 結果の解釈

# SHAPに基づきデータを解釈する
interpret_model(final_model)

HAP（Shapley Additive exPlanations）に基づいて予測結果を解釈する。
貢献度の高い順に上から説明変数が並んでいる。横軸はSHAP値であり、プロットの色は各説明変数の大小（青が小さく、赤が大きい）を表す。

例えばx8は大きいと（赤色系であると）SHAPの値はプラスであることが分かる。これはx8は目的変数と正の相関があると読み取れる。こちらで議論していますが、実際にx8はyと正の相関があり、今回のSHAPの結果が支持されます。

SHAPはtree系のモデルにしか対応していないので注意。例えば線形回帰モデルにSHAPを実行すると "This function only supports tree based models for binary classification: et, xgboost, lightgbm, dt, catboost, rf." とエラーが返ってくる。

参考
https://datadriven-rnd.com/shap/

interpret_model(final_model,plot="reason",observation=0)

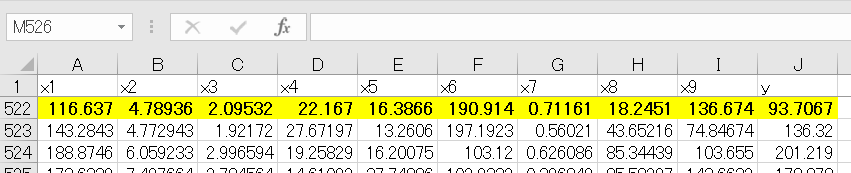
このようにSHAPを用いて個別に予測を確認することもできる。今回確認したデータは元のデータセットの521番目のデータである。base valueは特徴量の寄与を考慮しない目的変数の値である（データセットの目的変数の平均値とおおよそ一致するはずである）。このデータはx8=18.25であり、このx8の値が目的変数の値をグーンっと低くしていることが分かる。逆にx1やx5は目的変数を押し上げる要因になっていると読み取れる。

なお、x8は以下のような分布をしており、x8=18.25は平均よりもかなり小さく目的変数に対して負の寄与をしていると考えられる。

14. 決定木

# 小さな決定木のモデルを作って、特徴量の関係を可視化する
dt = create_model('dt', max_depth=3)
plot_model(dt, plot = 'tree')

これまでは個別にモデルを評価してきましたが、以下のコードを実行するとインタラクティブに各指標を確認できます。

# まとめてモデルを評価
evaluate_model(final_model)

15. モデルの確定

final_model = finalize_model(final_model)
print(final_model)

出力

Pipeline(memory=FastMemory(location=C:\Users\*ユーザー名に紐づく階層*\AppData\Local\Temp\joblib),
         steps=[('numerical_imputer',
                 TransformerWrapper(include=['x1', 'x4', 'x5', 'x6', 'x7', 'x8',
                                             'x9'],
                                    transformer=SimpleImputer())),
                ('categorical_imputer',
                 TransformerWrapper(include=[],
                                    transformer=SimpleImputer(strategy='most_frequent'))),
                ('actual_estimator',
                 LGBMRegressor(bagging_fraction=0.9, bagging_freq=2,
                               feature_fraction=0.9, learning_rate=0.05,
                               min_child_samples=16, min_split_gain=0.3,
                               n_estimators=240, num_leaves=6, random_state=123,
                               reg_alpha=1e-07, reg_lambda=5))])

公式のドキュメントでこのfinalize_modelを確認すると「This function doesn't change any parameter of the model. It only refits on the entire dataset including the hold-out set.」と書いてあり、ハイパーパラメータは変更しないが、fold-outしたデータも含めて全データ再度フィッティングしている。よって、このfinalizeしたモデルでテストデータを再度学習すると予測精度が変化（向上）する。試しに予測誤差をプロットすると先ほどより予測精度が向上していることが分かります。

plot_model(final_model, plot = 'error')

#　モデルの保存（　''の中は保存したいファイル名）
save_model(final_model,'saved_model')

保存したモデルは load_model('ファイル名') で読み込みが可能です。

16. 予測の実行

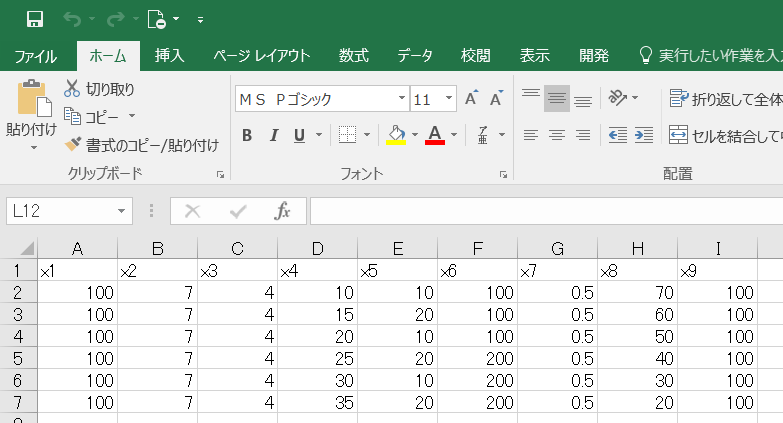
構築した予測モデルを使って予測をしていきます。ここでは以下のような自作のデータセット（csv）を用いて目的変数を予測していきましょう。

# 予測するデータを読み込む
data_unseen = pd.read_csv("df_new.csv")
data_unseen

読み込んだデータとモデルを組むために使ったデータの説明変数は一致させておく必要があるので注意

#　最終化したモデルで未知データの目的変数を予測
unseen_predictions = predict_model(final_model, data=data_unseen)
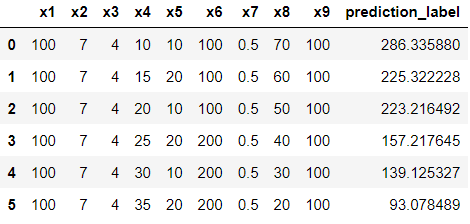
df_new_pred = pd.DataFrame(unseen_predictions)
df_new_pred

一番右の列に予測値が入力されていることが分かります。

# 予測値が入力されたデータフレームを出力する
df_new_pred.to_csv("df_new_pred.csv")

補足（学習とテストデータの分割）

読み込んだデータセットを学習とテスト（final modelに含めない）に分割する際は前処理前に以下のコードで学習に用いるデータ(data)とテストに用いるデータ(data_unseen)に分割する。

# モデリング用データと未知データの分割
# fracで割合を指定
data = df.sample(frac=0.80, random_state=123)
data_unseen = df.drop(data.index)
data.reset_index(drop=True, inplace=True)
data_unseen.reset_index(drop=True, inplace=True)

print('Data for Modeling: ' + str(data.shape))
print('Unseen Data For Predictions: ' + str(data_unseen.shape))
data_unseen.head()

【AutoMLで回帰】Pycaretで機械学習モデルの比較