はじめに
Pythonの機械学習ライブラリ「PyCaret」は、非常に簡単に動くライブラリですのでモデルの分析結果を出すまでは、初めての方でもサクサク出来るはずです。
ですが、モデルの種類や評価指標、解析結果の図の意味や見方がわからない場合「結局、どうしたらいいの?」という状況に陥ると思います。(私がそうでした・・・公式サイトは英語で、読むだけでも一苦労。)
このような中、共同でPyCaretを勉強してる方々の支えもあり色々と情報を仕入れることができましたので、私個人の備忘含め、PyCaretの全体像が理解できるようにこの記事に纏めてみました。
※細かい内容では無いことを予めお伝えしておきます。
※この記事は「回帰編」です。
「分類編」は「PyCaretの初心者向けまとめ(分類編)」を参照ください。
1.PyCaretとは
1-1.PyCaretとは
「PyCaret」とは、様々な種類の機械学習を少しのコードで実現してくれる便利なライブラリです。
公式サイトでは次のように紹介されています。
PyCaretは、Pythonのオープンソースのローコード機械学習ライブラリであり、仮説から考察までのサイクルタイムを短縮することを目的としています。
PyCaretを使用すると、選択したノートブック環境を使用して、データの準備からモデルのデプロイまで数秒で行うことができます。
https://pycaret.org/guide/ より引用
1-2.PyCaretのメリット
- コード実装が非常に簡単(数行で実装可能)
- データの前処理も自動で実施
- ハイパーパラメータの自動最適化が可能
- 色々な解析結果を図で確認が可能
1-3.PyCaretの実装手順
- PyCaretのインストール
- データの読み込み
- データの前処理
- 各種モデルの評価と精度の比較
- ハイパーパラメータの最適化
- モデルの精度の可視化
- モデルの確定
- 予測の実行
- 予測結果をCSVでダウンロード
2.環境・バージョン
- OS:windows10
- Jupyter Notebook:6.0.3
- PyCaret:2.2.1
3.PyCaretのインストール
まずは、pycaret のパッケージをインストールします。
※インストールに結構時間が掛かると思います。
pip install pycaret
4.データの読み込み
4-1.パッケージの読み込み
次に、必要なパッケージを読み込みます。
# パッケージの読み込み
import pandas as pd
from pycaret.regression import *
今回は「回帰」を行うのでpycaret.regressionとしました。
尚、モジュール一覧は次の通りです。
| モジュール | インポート方法 |
|---|---|
| 分類 | pycaret.classification |
| 回帰 | pycaret.regression |
| クラスタリング | pycaret.clustering |
| 異常検出 | pycaret.anomaly |
| 自然言語処理 | pycaret.nlp |
| アソシエーション分析 | pycaret.arules |
4-2.データの読み込み
次に、データを読み込みます。
手持ちデータか否かでやり方を分けて記載しています。
【今回の記事は手持ちではない場合で話を進めていきます。】
手持ちデータではない場合(とりあえずPyCaretを動かしたい場合)
PyCaretに用意されているデータ【PyCaret’s Data Repository】より回帰では定番といわれる
「ボストン地価データ」を使用します。
詳しくはコチラを参照してください。 https://pycaret.org/get-data/
# 使用するデータの読み込み
from pycaret.datasets import get_data
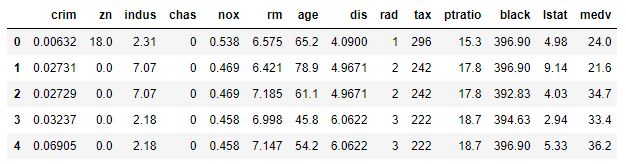
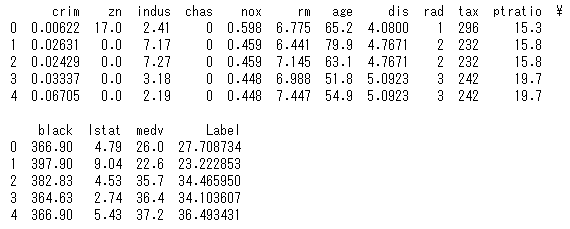
boston_data = get_data('boston')
| 項目名 | 説明 | データ型 |
|---|---|---|
| crim | 犯罪発生率(町ごとの一人当たり犯罪率) | float64 |
| zn | 25,000 平方フィート以上の住宅区画の割合 | float64 |
| indus | 小売業以外の商業が占める土地面積の割合 | float64 |
| chas | チャールズ川沿いかどうかのダミー変数 (1: 川沿い、 0: それ以外) | int64 |
| nox | 窒素酸化物の濃度(pphm単位) | float64 |
| rm | 1戸あたりの平均部屋数 | float64 |
| age | 1940年よりも前に建てられた物件の割合 | float64 |
| dis | ボストンにある5つの雇用施設までの重み付きの距離 | float64 |
| rad | 環状高速道路へのアクセス指数 | int64 |
| tax | 10,000ドルあたりの固定資産税の割合 | int64 |
| ptratio | 町ごとの生徒と教師の比率 | float64 |
| black | 1000(Bk – 0.63)^2 の値。BKは町ごとの黒人の割合。 | float64 |
| lstat | 低所得者の割合 (%) | float64 |
| medv | 住宅価格の中央値(単位 1000ドル) | float64 |
手持ちデータの場合(実務でPyCaretを動かす場合)
実務ではCSVファイルを読み込むケースが多いと思います。
その場合はPandasのpd.read_csvで次のように読み込んでください。
# CSVデータの読み込み
data = pd.read_csv('c:/path_to_data/file.csv')
[補足1]
上記のように引数を何も指定しないと、CSVファイルはUTF-8で読み込みます。
CSVファイルをShift-JISで読み書きしたいときには、引数で指定する必要があります。(以下、例)
data = pd.read_csv('c:/path_to_data/file.csv', encoding = "shift-jis")
[補足2]
WindowsでPythonを使う時の注意として、ファイルのパスを指定をする場合、
ファイルのパスを「¥」区切りで指定するとエラーになります。主な対処方法は次の2つです。
パスの区切りを¥¥にする
data = pd.read_csv('c:\\path_to_data\\file.csv', encoding = "shift-jis")
パスの区切りを/にする
data = pd.read_csv('c:/path_to_data/file.csv', encoding = "shift-jis")
5.データの前処理
次に、PyCaretを起動します。
# PyCaretを起動
exp1 = setup(boston_data, target = 'medv', ignore_features = None)
目的変数は住宅価格を意味する「medv」としています。
※setupコマンドの説明は下表の通りです。
| 項目 | 説明 | 備考 |
|---|---|---|
| 第一引数 | 解析に用いる読み込んだデータ | 必須 |
| 第二引数 | 予測に用いる目的変数の列名 | 必須 |
| 第三引数 | 分析から外す説明変数の列名 | 任意 |
実行すると次のように自動的にデータ型を設定してくれます。

データ型を変更せず、このまま続ける場合は"Enter"を押下します。
データ型の変更が必要な場合は、"quit"と入力し"Enter"を押下します。
例えば、chas 列はCategoricalとして認識されていますが、Numericとして扱いたい場合は
setupコマンドを次のようにオプションを記述します。
※オプション一覧はこちらが非常に参考になります。
# PyCaretを起動(データ型を変更する場合)
exp1 = setup(boston_data, target = 'medv', ignore_features = None, numeric_features = ['chas'])
※ numeric_features オプションを使用し、, numeric_features = ['chas']を追加しています。
これを実行すると、次のようにchas 列がNumericとして変更されていることがわかります。
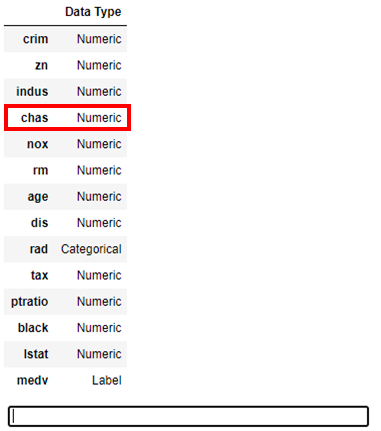
setupコマンドが完了すると次のようにセットアップ結果が表示されます。
データによっては算出できない項目もあるため、その場合は「False」や「None」と表示されます。
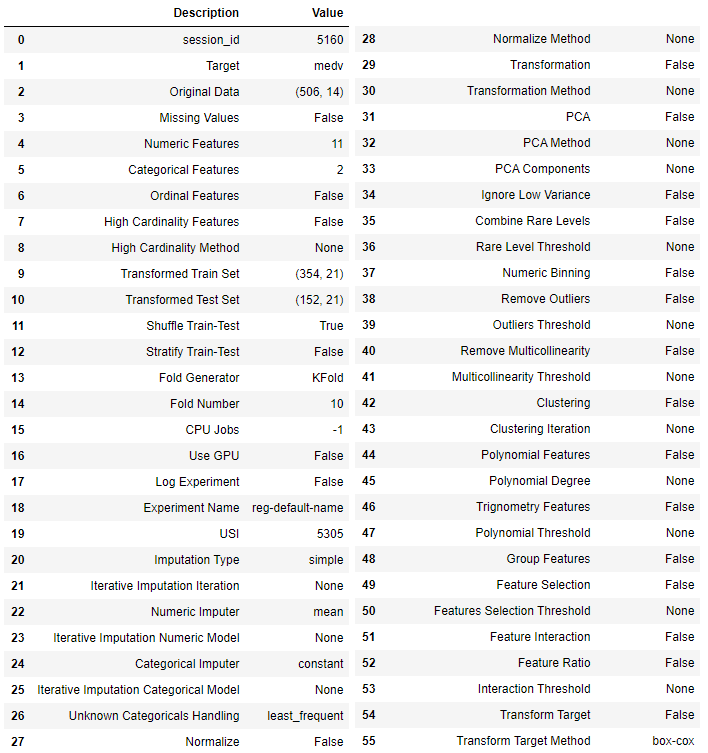
6.各種モデルの評価と精度の比較
6-1.モデルの比較
次に、モデルを比較します。
# モデルの比較
compare_models()
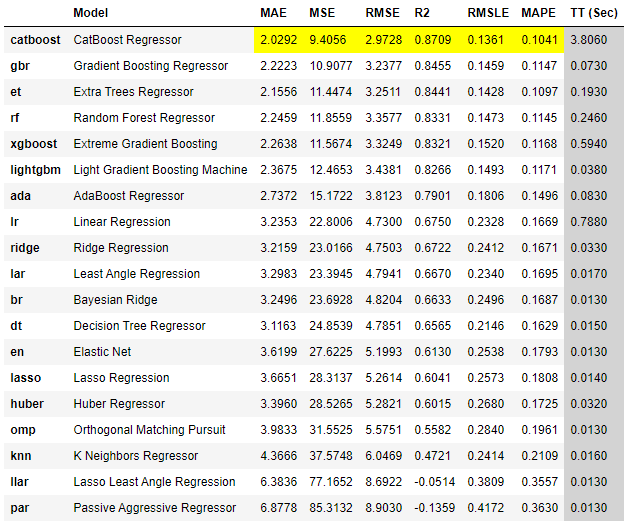
これを実行すると次のように各種モデルを評価・比較し誤差の少ない順番に並べた一覧が表示されます。
(回帰の場合、デフォルトではR2で並べ替えられます。)
この例の場合、「CatBoost Regressor」というモデルの評価が高いことがわかります。
※各評価指標のトップが黄色で網掛けされます。
ただし、この分析ではハイパーパラメータの最適化までは行われていません。(この後に最適化を進めます。)
尚、処理の概要は次のようになっています。
- 偏りなく、満遍なく教師データと検証データを入れ替えることを指す「交差検証(クロスバリデーション)」を実施
- デフォルトでは、教師データと検証データを7:3で分割し、Fold=10(データを10分割して、教師データと検証データを入れ替えている)として各種モデルの平均のスコアを表示している
6-2.評価指標について
回帰で使用される評価指標の概要と見方は次の通りです。(ここ重要です。)
MAE
MAE(Mean Absolute Error)では、予測値の誤差の大きさを評価します。
数式は下記の通りです。
\begin{eqnarray}
MAE = \frac{1}{N} \sum|y_i - \hat{y_i}|
\end{eqnarray}
$y_i$ : $i$番目サンプルの実測値
$\hat{y_i}$ : $i$番目サンプルの予測値
$N$ : サンプル数
| 項目 | 概要 |
|---|---|
| 判断基準 | ・0に近いほど良い値 |
| 解釈 | ・予測値と実測値の平均的なズレ(誤差)の大きさ |
| 特徴 | ・大きく予測を外したケースをあまり重要視していない ・MAEを基準として良いモデルを選ぶと最大誤差が大きくなる傾向にある ・RMSEに比べて外れ値の影響を受けにくい |
MSE
MSE(Mean Squared Error)では、大きな誤差を重要視して評価します。
数式は下記の通りです。
\begin{eqnarray}
MSE = \frac{1}{N} \sum(y_i - \hat{y_i})^2
\end{eqnarray}
$y_i$ : $i$番目サンプルの実測値
$\hat{y_i}$ : $i$番目サンプルの予測値
$N$ : サンプル数
| 項目 | 概要 |
|---|---|
| 判断基準 | ・0に近いほど良い値 |
| 解釈 | ・予測値と実測値のズレの大きさと解釈できる ・MAEと類似しているが、MAEのように実際の平均的な誤差とは異なる |
| 特徴 | ・大きく予測を外したケースを重要視している ・予測を大きく外すと大幅にMSEが大きくなる傾向にある |
RMSE
RMSE(Root Mean Squared Error)では、大きな誤差を重要視して評価します。
数式は下記の通りです。
\begin{eqnarray}
RMSE = \sqrt{\frac{1}{N} \sum(y_i - \hat{y_i})^2}
\end{eqnarray}
$y_i$ : $i$番目サンプルの実測値
$\hat{y_i}$ : $i$番目サンプルの予測値
$N$ : サンプル数
| 項目 | 概要 |
|---|---|
| 判断基準 | ・0に近いほど良い値 |
| 解釈 | ・予測値と実測値のズレの大きさと解釈できる ・MAEと類似しているが、MAEのように実際の平均的な誤差とは異なる |
| 特徴 | ・大きく予測を外したケースを重要視している ・予測を大きく外すと大幅にRMSEが大きくなる傾向にある ・回帰モデルの最も一般的な性能評価指標として用いられる |
R2(決定係数)
決定係数$R^2$では、推定された回帰モデルの当てはまりの良さを評価します。
数式は下記の通りです。
\begin{eqnarray}
R^2 = 1 - \sum \frac{(y_i - \hat{y_i})^2}{(y_i - \bar{y})^2}
\end{eqnarray}
$y_i$ : $i$番目サンプルの実測値
$\hat{y_i}$ : $i$番目サンプルの予測値
$\bar{y}$ : 実測値の平均
| 項目 | 概要 |
|---|---|
| 判断基準 | 0.6以下:全然予測できてない 0.8以上:良いモデル 0.9以上:過学習の可能性あり |
| 解釈 | ・回帰モデルの当てはまりの良さを評価 |
| 特徴 | ・説明変数が多くなると1に近づいていく ・非線形モデルを評価することはできない |
RMSLE
RMSLE(Root Mean Square Logarithmic Error)では、予測値の誤差の大きさを比率や割合で評価します。
数式は下記の通りです。
\textrm{RMSLE} = \sqrt{\frac{1}{N}\sum_{i=1}^{N}(\log (1+y_{i})-\log (1+\hat{y}_{i}))^{2}}
$y_i$ : $i$番目サンプルの実測値
$\hat{y_i}$ : $i$番目サンプルの予測値
$N$ : サンプル数
| 項目 | 概要 |
|---|---|
| 判断基準 | ・0に近いほど良い値 |
| 解釈 | ・予測値と実測値のズレの大きさをを比率や割合で解釈できる |
| 特徴 | ・目的変数のとりうる値の範囲が広いデータに利用 |
MAPE
MAPE(Mean Absolute Percentage Error)では、実測値の大きさあたりの予測誤差の大きさを評価します。
数式は下記の通りです。
\begin{eqnarray}
MAPE = \frac{1}{N} \sum|\frac{y_i - \hat{y_i}}{y_i}|
\end{eqnarray}
$y_i$ : $i$番目サンプルの実測値
$\hat{y_i}$ : $i$番目サンプルの予測値
$N$ : サンプル数
| 項目 | 概要 |
|---|---|
| 判断基準 | ・0に近いほど良い値 |
| 解釈 | ・実測値の大きさに対する予測値の平均的なズレ(誤差)の割合 |
| 特徴 | ・実測値に対する予測誤差の割合の大きさを重要視している ・実測値が0を取るケースでは使用できない |
6-3.モデルの種類
回帰では、次のモデルが搭載されています。
| ID(引数) | モデル名 | 概要 |
|---|---|---|
| catboost | CatBoost Regressor | ・キャットブースト ・決定木ベースの勾配ブースティングに基づくモデル ・カテゴリカル変数(質的変数)の扱い方が上手い ・決定木のツリー構造を最適にして過学習を防ぐ ・XgboostやLightGBMよりも精度が高くなる可能性がある |
| gbr | Gradient Boosting Regressor | ・勾配ブースティング ・弱い予測モデル(決定木)のアンサンブル形式で生成したもの |
| et | Extra Trees Regressor | ・エクストラツリー ・Random Forestと同じようにランダムな木を複数用意してバギングする ・ブートストラップサンプリングはせずに訓練データ全てを用いる ・シンプルで高速に動き、分類精度もRandom Forestに匹敵する |
| rf | Random Forest | ・ランダムフォレスト ・決定木の王道といわれている ・決定木をたくさん集めて並列に扱う手法(バギング) |
| xgboost | Extreme Gradient Boosting | ・エックスジーブースト ・ブースティングという手法で決定木を直列に扱う ・精度が比較的高いが、学習に時間が掛かる |
| lightgbm | Light Gradient Boosting | ・ライトジービーエム ・xgboostの軽量版的なモデル ・精度の上げるためには特徴量の調整が必要 |
| ada | AdaBoost Regressor | ・アダブースト ・勾配ブースティング系アルゴリズムの走り ・直前の弱識別器で誤ったサンプルに対する重みを大きくして学習を行う |
| lr | Linear Regression | ・線形回帰 ・線形モデルによる回帰分析を行う |
| ridge | Ridge Regression | ・リッジ回帰 ・過学習を抑える手法の一つ ・線形回帰に正則化項(ペナルティ項)としてL2ノルムを導入したモデル |
| lar | Least Angle Regression | ・最小角回帰(LARS) ・Lassoの推定アルゴリズム |
| br | Bayesian Ridge | ・ベイズ線形回帰 ・最適解を含めて分布として捉えようとするモデル |
| dt | Decision Tree | ・決定木 ・条件による分岐を「根」からたどることで、最も条件に合致する「葉」を検索するアルゴリズム ・決定木単体では弱い予測モデル |
| en | Elastic Net | ・エラスティックネット ・リッジ回帰とラッソ回帰の折衷案のモデル ・Lasso回帰のモデルに取り込める説明変数の数に制限がある」という問題点をカバー |
| lasso | Lasso Regression | ・ラッソ回帰 ・不要なパラメータ(次元や特徴量)を削ることができる手法の一つ ・線形回帰に正則化項(ペナルティ項)としてL2ノルムを導入したモデル |
| huber | Huber Regressor | ・フーバー回帰 ・ロバスト回帰で使われる損失勘定の1つ ・外れ値が大きくても引きづられにくいモデル |
| omp | Orthogonal Matching Pursuit | ・直交マッチング追跡(OMP) ・貪欲法の1つ |
| knn | K Neighbors Regressor | ・K近傍法 ・次元の呪いのため、高次元データには向かない ・トレーニングデータ数・特徴量が増えると予測が遅くなる |
| llar | Lasso Least Angle Regression | ・ラッソ最小角回帰 ・LARSを使ったラッソ回帰 |
| par | Passive Aggressive Regressor | ・PA ・オンライン機械学習のアルゴリズムの一つ ・訓練事例を正しく分類できなかった場合重みを更新 |
| ard | Automatic Relevance Determination | ・関連度自動決定(ARD) ・目的変数に対する個々の説明変数の寄与の大きさを見積もる手法 |
| ransac | Random Sample Consensus | ・RANSAC ・外れ値をうまく無視して法則性(パラメータ)を推定をする手法 |
| tr | TheilSen Regressor | ・テイルセン回帰 ・外れ値の影響を受けないモデル |
| kr | Kernel Ridge | ・カーネルリッジ回帰 ・カーネル法を回帰問題に適用したもの |
| svm | Support Vector Machine | ・サポートベクターマシン(SVM) ・認識性能が優れた学習モデルの一つ ・未学習データに対して高い識別性能を得るための工夫がある |
| mlp | Multi Level Perceptron | ・多層パーセプトロン(MLP) ・複数の形式ニューロンが多層に接続されたネットワーク ・現在の機械学習の基盤となっている |
※上表のIDは次項で記載のcreate_modelの引数として使用します。
7.ハイパーパラメータの最適化
7-1.モデルの作成
次に、モデルを作成します。
今回は、決定木系の王道といわれる「Random Forest(ランダムフォレスト)」のモデルを作成します。
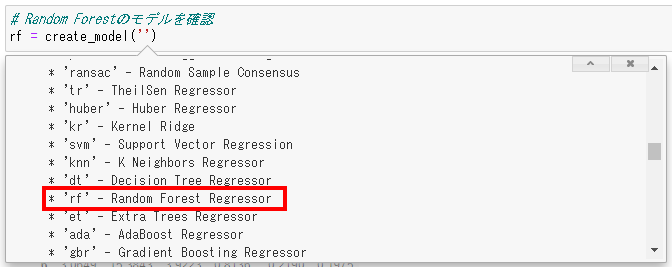
# Random Forestのモデルを作成
rf = create_model('rf')
尚、create_modelの引数は、windowsの場合は引数を記入する箇所で「Shift+Tab」のショートカットキーを使うとツールチップが表示されますので、コチラの内容を指定します。(上記、6-3.モデルの種類のID(引数)のことです。)
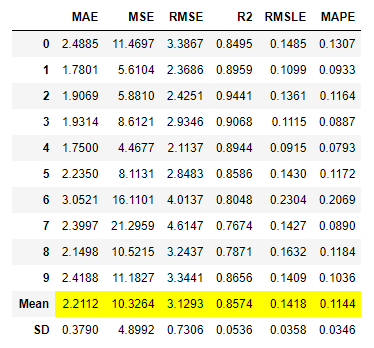
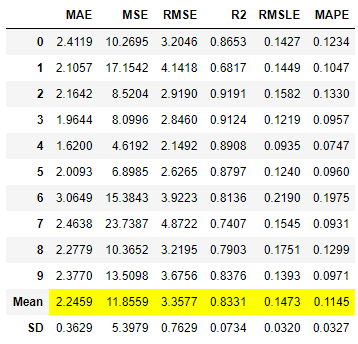
これを実行すると次のように初期設定である交差検証「10回」にて、検証が行われています。
Mean(平均値)、SD(標準偏差)も同時に表示されています。
7-2.ハイパーパラメータの最適化
次に、ハイパーパラメータの最適化を行います。
# Random Forestのモデルを最適化
tuned_rf = tune_model(rf, n_iter = 500, optimize = 'r2')
※tune_modelコマンドの説明は下表の通りです。
| 項目 | 説明 | 備考 |
|---|---|---|
| 第一引数 | モデルの名称 | 必須 |
| 第二引数 | ランダムグリッドサーチの回数 | 任意 |
| 第三引数 | 最適化の対象 ※デフォルトは「R2」 | 任意 |
これを実行した結果(最適化後)と実行前を比較すると、R2が「0.8331」から「0.8574」と増加し最適化が行われたことが確認できます。※PyCaretの最適化はランダムグリッドサーチが採用されています。
8.モデルの精度の可視化
次に解析した結果を可視化します。
# 解析結果の確認
evaluate_model(tuned_rf)
これを実行すると、解析結果を選択できるタブが表示されます。
回帰でプロットされるモデルの概要と見方はそれぞれ次の通りです。(ここ重要です。)

Hyperparameters(ハイパーパラメータ)
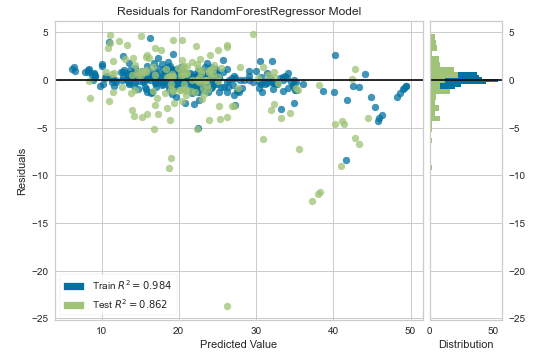
Residuals(残差プロット)
こちらは、残差プロットです。
横軸に予測値、縦軸に残差をプロットします。良い予測モデルであれば、残差と予測値は相関しないので、残差0のところに横に並ぶようなプロットになります。残差はランダムな誤差になるはずなので、ヒストグラムは正規分布になります。
外れ値が生じるケースは、以下の通りです。
- 回帰式が適切ではない
- データが不適切
- 学習不足
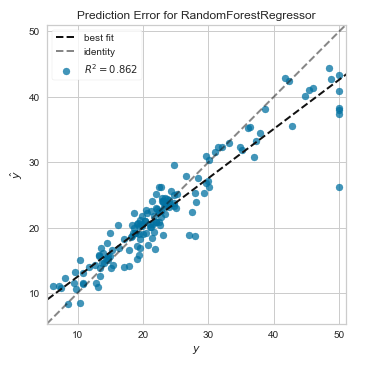
Prediction Error(予測誤差プロット)
こちらは予測誤差プロットです。
横軸に実際の値を、縦軸に予測値をプロットしたものです。予測が完全であれば、傾き1の直線上に点が乗ります。点が傾き1の直線周辺に集まるモデルが良いモデルになります。
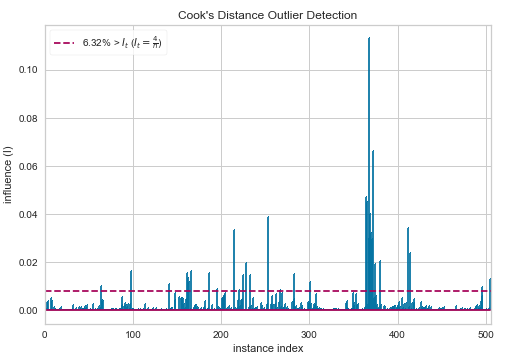
Cooks Distance(クックの距離のプロット)
こちらはクックの距離のプロットです。
クックの距離とは、「i番目の観測値を使用して計算された係数と、観測値を使用しないで計算された係数との間の距離に対する測度」です。図中の破線が、推奨される閾値です。これ以上は「外れ値の可能性あり」と判断できます。
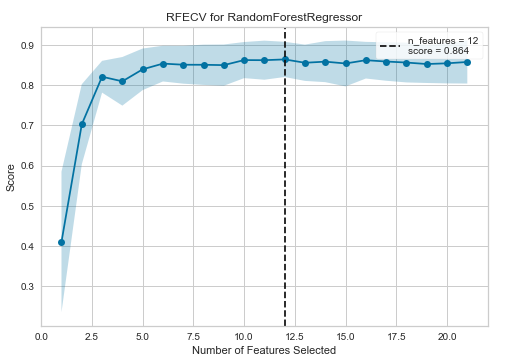
Feature Selection(特徴量選択)
こちらは特徴量選択です。
特徴量(説明変数)の選択数に応じて予測スコアを折れ線グラフとして表示するものになっています。グラフの横軸が特徴量の数で、縦軸が予測精度を表し、予測精度が最大の特徴量数のところに縦に点線が引かれます。
今回の場合、特徴量の個数が12個のときに最大スコア「0.864」になったことがわかります。
特徴量選択の特徴量の選択優先順位は後述するFeature Importance(特徴量の重要度)の順位が高いもの(モデルの予測精度に大きく寄与している説明変数)から選択されています。
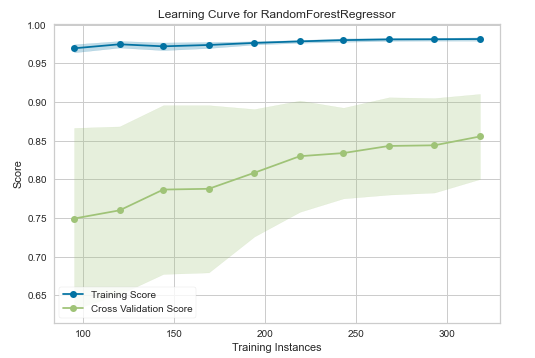
Learning Curve(学習曲線)
こちらは学習曲線です。
データ数に応じた予測精度を表示するグラフで、横軸にデータサイズ、縦軸に予測精度をプロットしています。
良いモデルの指標としてはデータが増えるごとにtraining scoreが減少し、cross validation scoreが増加することが望ましいといわれています。もし、cross validation scoreとtraining scoreの差が大きかった場合は、学習数が足りてない恐れがあるため、データ数を増やすことでモデルの精度の向上が図れるかもしれません。
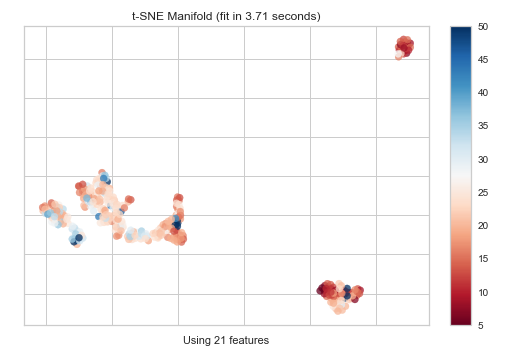
Manifold Learning(多様体学習)
こちらは多様体学習です。
高次元データ(説明変数が複数あるもの)を2次元に落としてプロットしたグラフです。この多様体学習では、t-SNE(ティースニ) (t-Distributed Stochastic Neighbor Embedding)(t分布型確率的近傍埋め込み法)が使用されています。t-SNEの主な目的は、高次元データの視覚化です。したがって、データが2次元または3次元に埋め込まれる場合に最適に機能します。
新しい特徴量を加える場合や高次元のデータセットを扱う場合には、最も有用な特徴量だけを残して残りを捨てて特徴量の数を減らす(次元削減)のは良い考えだと言われています。なぜなら次元削減をすることでモデルが単純になって解釈しやすくなるだけでなく、汎化性能が向上するからです。
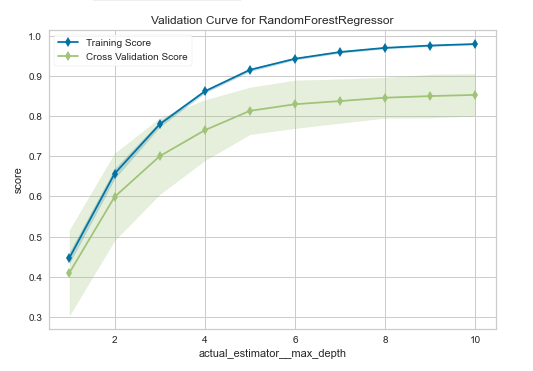
Validation Curve(検証曲線)
こちらは検証曲線です。先述の学習曲線に似ています。
ハイパーパラメーターの値を変えた時の予測精度を表示するグラフで、横軸にハイパーパラメータ、縦軸に予測精度をプロットしています。一つのハイパーパラメータがどれくらい寄与するか見たいときに使用します。適切なハイパーパラメータ(例:max_depth:木の深さ)の値はどこかを確認でき、訓練精度と検証制度の差が小さく、精度が高いものを選ぶようにします。(学習不足や過学習を確認することができます。)
尚、薄く塗りつぶされた範囲は、クロスバリデーション(交差検証)により求められた精度の最大値と最小値の範囲を表しています。
また、横軸のハイパーパラメータは使用する学習モデル(アルゴリズム)によって異なります。詳細は次の通りです。
| 学習モデル | 横軸 |
|---|---|
| Decision Tree Random Forest Gradient Boosting Regressor Extra Trees Regressor Extreme Gradient Boosting Light Gradient Boosting CatBoost Regressor |
max_depth |
| Support Vector Machine | C |
| Multi Level Perceptron Ridge Regression |
alpha |
| AdaBoost Regressor | n_estimators |
| K Neighbors Regressor | n_neighbors |
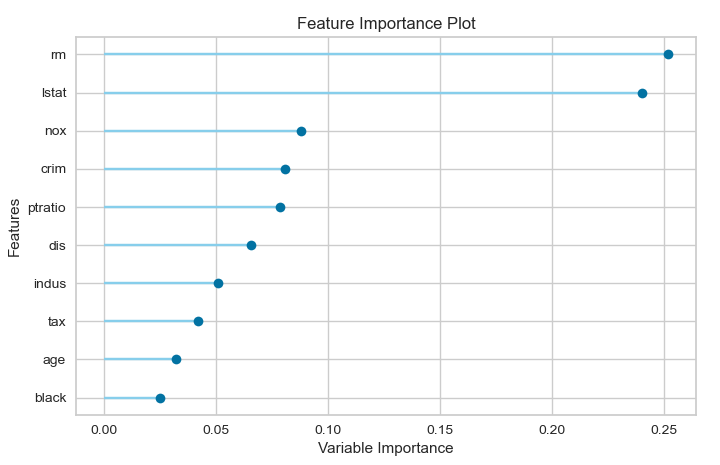
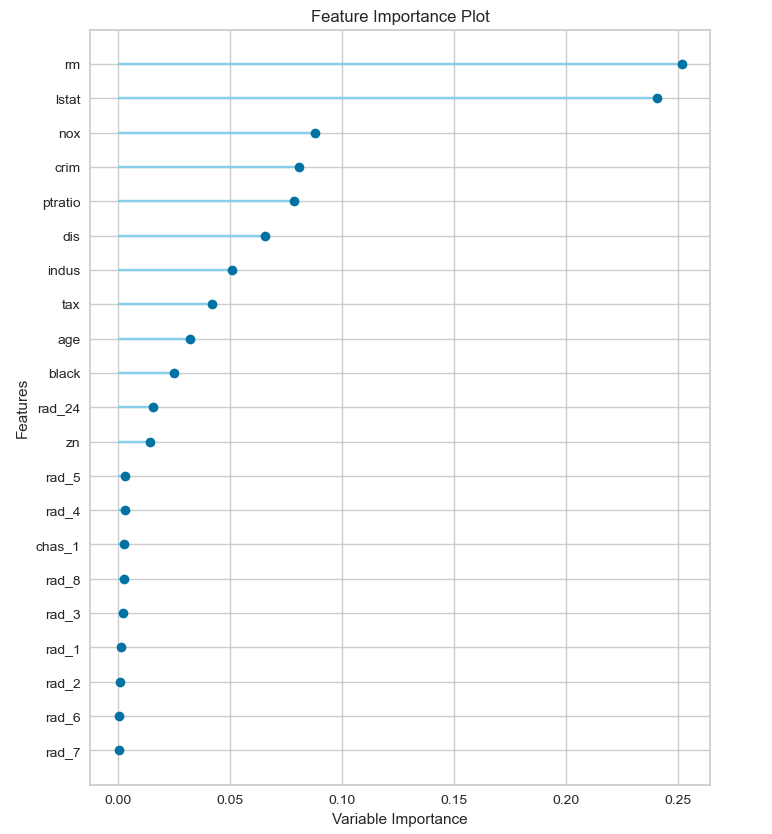
Feature Importance(特徴量の重要度)
こちらは特徴量の重要度です。
目的変数に及ぼす影響が大きい順に上から特徴量が表示されています。(上位10位まで)
Feature Importance(ALL)(特徴量の重要度(全ての特徴量))
こちらは特徴量の重要度(全ての特徴量)です。
Feature Importance(特徴量の重要度)では、上位10位の特徴量が表示されていますが、ここでは解析に用いたデータの全ての特徴量を表示します。
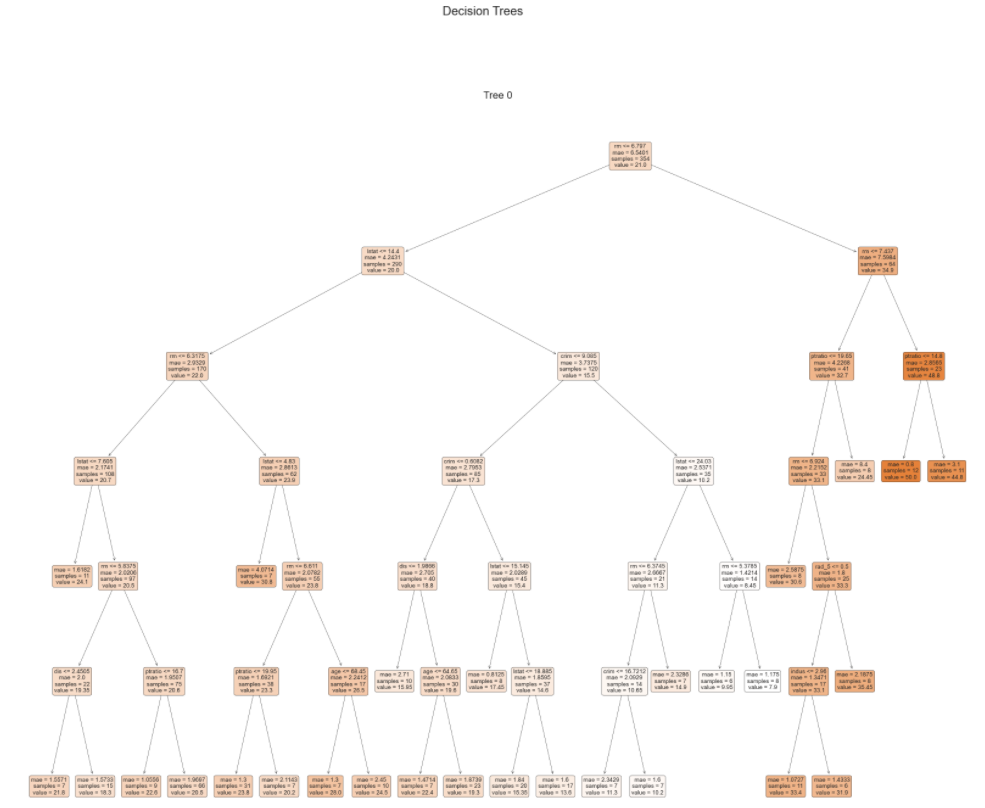
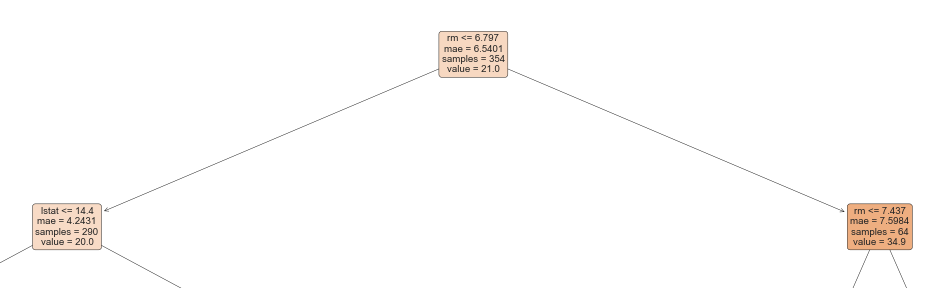
Decision Tree(決定木)
※「Random Forest(ランダムフォレスト)」では表示されないため、「Decision Tree(決定木)」の結果で解説
こちらは決定木です。
木構造を用いて分類や回帰を行う機械学習の手法の一つで、比較的単純なモデルですが、モデルをツリーで表現できるので、どの説明変数が目的変数にどのように効いているのかが視覚的に分かりやすいというメリットがあります。
9.モデルの確定
次に、モデルを確定します。(当然ながら解析結果などを考慮したうえで)
# モデルの確定
final_rf = finalize_model(tuned_rf)
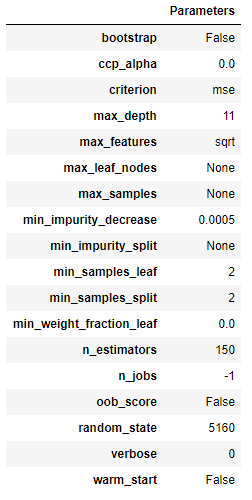
print(final_rf)
実行すると次のような最適化されたハイパーパラメータを確認することができます。
これで、学習済みのモデルができあがりました。

10.予測の実行
学習済みモデルが出来上がったら、未知なるデータを投入してみます。
(今回は、ボストン地価データを用いていましたので、未知なるデータは適当なものを準備しました。)
data_unseenという名前のデータフレームに入れます。
# 未知なるデータを読み込む
data_unseen = pd.read_csv('c:/path_to_data/unseen_boston.csv')
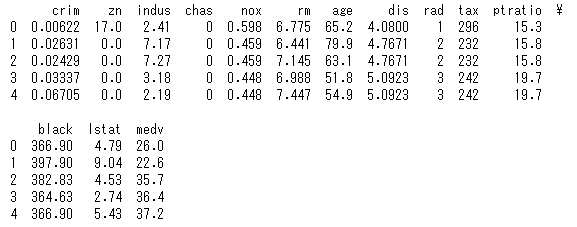
print(data_unseen)
これを実行すると次のように未知なるデータが読み込まれます。
この”unseen_data” を、今回作成した予測モデルに投入し、価格の予測を行わせてみます。
# 予測の実行
unseen_predictions = predict_model(final_rf, data = data_unseen)
print(unseen_predictions)
これを実行すると次のように予測値がLabelとして追加されているのが分かります。
本来は未知のデータについて、目的変数であるmedvは分からないのですが、今回は適当に未知なるデータを準備したのでmedvがデータに入っています。
適当な未知なるデータなので、何とも言えませんが、未知なるデータの価格medvと予測モデルが予測した予測値であるLabelを比べると、まずまずな感じの値が出ていることがわかります。
11.予測結果をCSVでダウンロード
次に、予測した結果をCSVファイルでダウンロードしてみます。
実務では予測した結果を何らかに利用することになるかと思います。
# CSVファイルでダウンロードする
unseen_predictions.to_csv('unseen_data_predicted_Label.csv')
これを実行すると、次のようにCSVファイルがダウンロードされます。

12.まとめ
実際に私がPyCaretを使ってみてPyCaretを扱う上で大切になるだろうと思ったことは次の4点でした。
- 大前提として取扱うデータをよく理解すること
- モデルの種類とそれぞれのモデルの特徴を理解すること
- 評価指標の種類と見方を理解すること
- 解析結果(図)の種類と見方を理解すること
※使いこなしてきたらデータ型やハイパーパラメータの調整ができることが大切になるのだろうと思いました。
13.参考文献
- PyCaret公式サイト
- scikitlearn公式サイト(データセット)
- RIGHTCODEブログ 機械学習の自動化を可能にする「PyCaret」の実力を把握してみる
- Tableauから始めるデータサイエンス PyCaret を使って東京の中古マンション価格を予測してみよう!
- PyCaretのsetup関数の引数について
14.最後に
いかがでしたでしょうか?
とりあえずPyCaretを使えて、全体像を理解いただけていれば幸いです。
細かい内容は無いので、隔靴掻痒(痒い所に手が届かない)な点はご容赦ください。
PyCaretリリース前の時代を知らない私からすると便利なPyCaretにこれから頼ってしまいそうな予感です。(これで本当にいいのか?とも思いますが。)
この界隈の玄人の方からするとPyCaretは自動車でいうところのAT車のような感じで見られているのかな?とも思います。「MT車のシフトチェンジこそが、最大燃費を叩き出す!」みたいなイメージでしょうか?
とにもかくにも、初心者の私にとっては、データサイエンスの取っ掛かりとしてPyCaretは最高のライブラリだと感じました。最後までお付き合いいただきましてありがとうございました。