最短超文字列問題

本記事は、「文字列アルゴリズム Advent Calender 2017」 9日目の記事です。
8日目の記事は @kampersanda 氏による「ダブル配列で決定性有限オートマトンを表現する」でした。
10日目の記事は @tsukasa_diary 氏による「BDDとZDD -ブール関数と集合族の圧縮処理-」です。

ちなみに私は去年の Advent Calender では 、Range Minimum Query という記事も書いています。お時間のある方はそちらもぜひご覧ください。

また、本記事の内容はこちらの論文[1]に書かれています。
さらに日本語のこちらの本[2]にも、書かれていたはずです(私の記憶が正しければ...)。

はじめに

本記事では、最短超文字列問題¹という問題を扱います。
最短超文字列問題は、文字列の集合が与えられたときに、
それらすべてを部分文字列として含む文字列（超文字列）のうち
最短のものを求めるという問題です。

この問題は、生物学の分野に応用することができます。
塩基配列の断片から元の配列を復元するような操作をしたいとき、
最短超文字列問題を解くことで尤もらしい配列を復元できると思われます。

残念ながらこの問題は NP 困難²であることが知られており、
P = NP でない限り、この問題を解く多項式時間アルゴリズムは存在しません。
本記事では、厳密解を求めるアルゴリズムではなく、
近似解を求める多項式時間アルゴリズムを紹介します。

諸定義

ここでは、本記事で扱う問題と記法を定義します。

最短超文字列問題

文字列に関する基本的な定義・記法はこの記事に準じます。
細かい部分は省略させていただきます。
最短超文字列問題は、次のような問題です。

入力：文字列の集合 $S = \{s_1, s_2, ..., s_n\}$
出力：$S$ 中のすべての文字列を部分文字列として含む最短の文字列の長さ

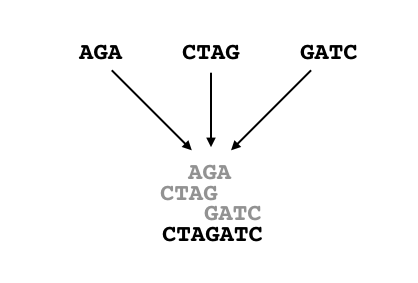
例えば、入力として $S = \{AGA, CTAG, GATC\}$ が与えられたとき、
$S$ に対する最短超文字列は、$CTAGATC$ となります（下図参照）。
$CTAGATC$ 中には $AGA, CTAG, GATC$ すべてが存在していることがわかりますね。
また、ここでは確認はしませんが、これは $S$ に対する超文字列の中で最短です。
よって、解はその長さ $7$ となります。

また、今回は簡単のため、入力の文字列集合 $S$ は以下を満たすと仮定します。

$S$ 中の任意の2つ文字列 $s_i, s_j,(i \neq j)$ に対して、$s_i$ は $s_j$ の部分文字列でない

記法

ここでは、本記事で利用する記法をいくつか定義します。
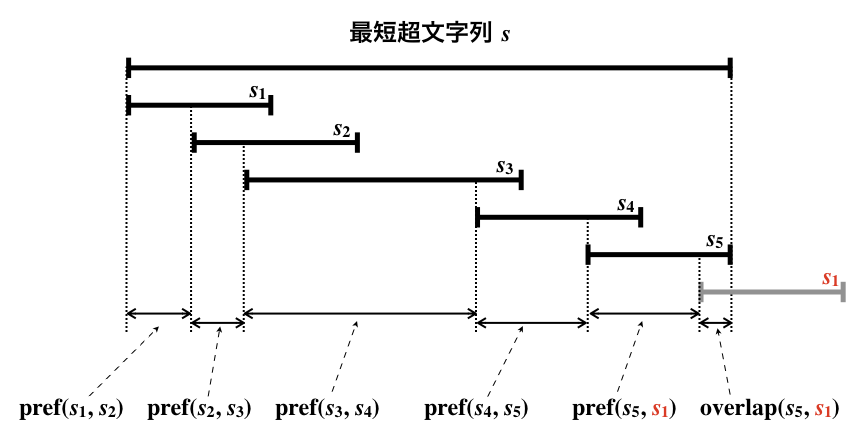
任意の文字列 $s, t$ に対して、$s$ の接尾辞かつ $t$ の接頭辞である文字列のうち
最も長いものを $overlap(s, t)$ と表します。
また、$s$ の末尾から $overlap(s, t)$ を削ったものを、$pref(s, t)$ と表します。
$s, t$ の順番によって文字列が異なることに注意してください。

上図のように $s, t$ をオーバーラップさせて作った超文字列（の短い方）を $u$ とします。
すると、$u = pref(s, t)t$ です。
さらに $t = pref(t, s)overlap(t, s)$ であることを考えると、
$u = pref(s, t)pref(t, s)overlap(t, s)$ であることが言えます。
わざわざ冗長な見た目にしましたが、こうすることで $u$ の長さ $|u|$ が
$|u| = |pref(s, t)| + |pref(t, s)| + |overlap(t, s)|$
であることがわかると思います。
超文字列の長さを $|pref(\cdot,\cdot)|$ と $|overlap(\cdot,\cdot)|$ だけで表すことができました。

この考えを一般化して、最短超文字列問題に適用させます。
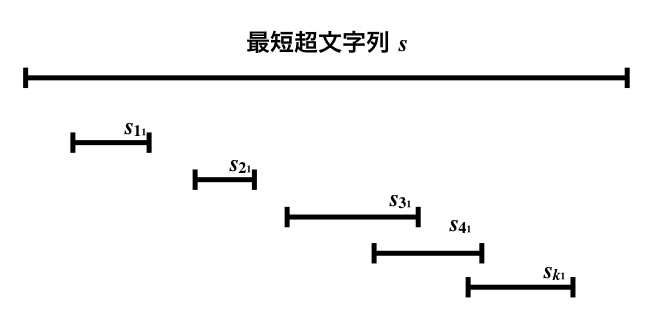
最短超文字列問題の最適解 $OPT(S)$ は、ある置換 $\pi$ を用いて

OPT(S) = |pref(s_{\pi(1)}, s_{\pi(2)})| + |pref(s_{\pi(2)}, s_{\pi(3)})| + ... |pref(s_{\pi(n)}, s_{\pi(1)})| + |overlap(s_{\pi(n)}, s_{\pi(1)})|

と表されます³。
超文字列の長さが上記の式で表されるイメージを下図に示します。

巡回セールスマン問題と最小閉路被覆問題

今回紹介する近似アルゴリズムでは、最短超文字列問題を
最小閉路被覆問題⁴というグラフの問題に帰着させます。
ここでは、その帰着を説明をするための準備をします。

プレフィックスグラフ

最短超文字列問題の入力文字列集合 $S$ から、
以下のような辺重み付き有向グラフ $G_S = (V, E)$ を構築します。

$V = \{v_1, v_2, ..., v_n\}$, ただし、各 $v_i$ は文字列 $s_i$ に対応。
$E = \{(v_i, v_j) | 1 \leq i, j \leq n, i \neq j\}$, ただし、辺$(v_i, v_j)$の重みは $|pref(s_i, s_j)|$

このとき、$G_S$ を、$S$ に対するプレフィックスグラフと呼ぶことにします。
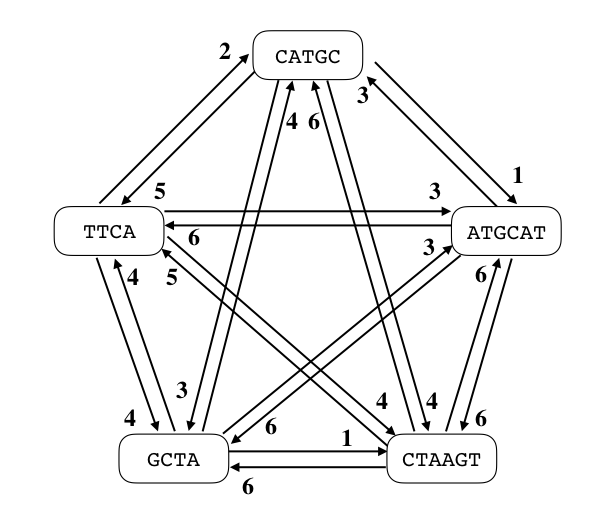
例えば $S = \{CATGC, ATGCAT, CTAAGT, GCTA, TTCA\}$ であった場合、
$G_S$ は下図のようなグラフになります。

巡回セールスマン問題

最小閉路被覆問題を紹介する前に、巡回セールスマン問題を定義します。
これは有名な問題なので、詳細はぐぐってください。

入力：辺重み付き有向グラフ
出力：各頂点をちょうど1度だけ通る、重み合計最小の閉路（の重み合計)

※本記事では、閉路そのものよりも、閉路の重みの値を気にします。

入力が $G_S$ である場合の巡回セールスマン問題の最適解を $TSP(S)$ で表します⁵。
すると、必ず $TSP(S) \leq OPT(S)$ となります。
証明は真面目にはしませんが、おおまかなアイデアを以下に書きます。

プレフィックスグラフと巡回セールスマン問題の定義から、$TSP(S)$ は
$TSP(S) = |pref(\cdot,\cdot)| + ... + |pref(\cdot,\cdot)|$
という形をしていることがわかります。一方の $OPT(S)$ は
$OPT(S) = |pref(\cdot,\cdot)| + ... + |pref(\cdot,\cdot)| + |overlap(\cdot,\cdot)|$
という形をしていました。

文字列をどんな順番で並べても $OPT(S) < TSP(S)$ とは
絶対になりえない！というイメージが伝わったでしょうか。。。

巡回セールスマンもまた NP 困難問題であるので、
この問題に帰着ができても何も嬉しくありません。
そこで、最小閉路被覆問題が登場します。

最小閉路被覆問題

最小閉路被覆問題は、以下のような問題です。

入力：辺重み付き有向グラフ
出力：各頂点をちょうど1度だけ通る、重み合計最小の閉路集合(の重み合計)

あえて、巡回セールスマン問題と対比的な書き方をしました。
巡回セールスマン問題との違いは、閉路が1つでなく、任意の個数まで許されているところです。
この問題に対しては、多項式時間アルゴリズムが知られています。

また、重要な事実として、入力のグラフが同じ場合は、
最小閉路被覆問題の最適解は巡回セールスマン問題の最適解以下である
ということが言えます。問題設定の差異を考えれば、ほぼ自明ですね⁶。
つまり、$G_S$ 上の最小閉路被覆問題の最適解を $CCP(S)$ とすると、
$CCP(S) \leq TSP(S)$ が成り立ちます。
$TSP(S) \leq OPT(S)$ であったので、$CCP(S) \leq TSP(S) \leq OPT(S)$ が言えます。

ここで TSP とはお別れです。欲しかったのはコレ、

CCP(S) \leq OPT(S)

この式は近似率の解析のときに使います。

4近似アルゴリズム

いよいよここから、アルゴリズムの紹介です！！
...と言いたいところですが、あと少しだけ追加で定義をさせてください。。

閉路に対応する文字列

$G_S$ 上の任意の閉路 $c_i$ を考えます。
$c_i$ はある頂点 $v_{i_1}$ から始まり、頂点 $v_{i_2}, v_{i_3}, ... v_{i_l}$ を経由して
$v_{i_1}$ に戻ってくる閉路であるとします。
このとき $c_i$ に対応する文字列 $\alpha(c_i)$ を、通った頂点に応じて以下のように定義します。
$\alpha(c_i) := prefix(s_{i_1} ,s_{i_2})... prefix(s_{i_l} ,s_{i_1})$
ここで閉路 $c_i$ の辺重みの合計値を $w(c_i)$ とすると、$|\alpha(c_i)| = w(c_i)$ が言えます。

また、$\alpha(c_i)$ の末尾に文字列を追加した $\sigma(c_i)$ を以下のように定義します。
$\sigma(c_i) := \alpha(c_i)s_{i_1}$
末尾にわざわざ $s_{i_1}$ を加えて何が嬉しいかというと、こうすることにより、
$\sigma(c_i)$ が $\{s_{i_1} ,s_{i_2}, ..., s_{i_l}\}$ の超文字列となるのです。
これにより、最短超文字列問題と最小閉路被覆問題の2人の間は結ばれます。

アルゴリズム

いよいよアルゴリズムの紹介です！4行になりました。

1. $S$ から $G_S$ をつくる

1. $G_S$ の最小閉路被覆 $\{c_1, c_2, ..., c_k\}$ を計算する
2. $s := \sigma(c_1)\sigma(c_2)...\sigma(c_k)$ を計算する
3. $s$ の長さ $|s|$ を出力する

ここまでの議論から、このアルゴリズムによって計算される文字列 $s$ は
$S$ の超文字列であることがわかります。
また、1.〜4. のいずれの操作も、多項式時間で行えます。
あとは、$|s|$ の値が $4OPT(S)$ 以下であることが言えれば、今回の証明は完了です。

4近似の証明

上記のアルゴリズムの出力を $ALG(S)$ で表します。つまり、$ALG(S) := |s|$ とします。
$s$ について考えて、単純な式変形をしてみます。

\begin{align}
s &= \sigma(c_1) + ... + \sigma(c_k)\\
  &= \alpha(c_1)s_{1_1}...\alpha(c_k)s_{k_1}\\\\
ALG(S) = |s| &= |\alpha(c_1)...\alpha(c_k)| + |s_{1_1}...s_{k_1}|\\
           &= \sum^{k}_{i=1}|\alpha(c_i)| + |s_{1_1}...s_{k_1}|\\
           &= CCP(S) + |s_{1_1}...s_{k_1}|\\
           &\leq OPT(S) + |s_{1_1}...s_{k_1}|
\end{align}

目標は4近似の証明、すなわち $ALG(S) \leq 4OPT(S)$ の証明であったので、
$|s_{1_1}...s_{k_1}| \leq 3OPT(S)$ が言えれば証明完了です。

当たり前ですが、$S$ に対する最短超文字列 $s$ 中には、
$s_{1_1}, ..., s_{k_1}$ はすべて出現します。
ここで一般性を失わず、その出現順は $s_{1_1}, ..., s_{k_1}$ の順番であるとします。

すると、
$\sum_{i=1}^{k}|s_{i_1}| - \sum_{i=1}^{k-1}overlap(s_{i_1}, s_{i+1_1}) \leq OPT(S)$
であることが言えるので
$|s_{1_1}...s_{k_1}| = \sum_{i=1}^{k}|s_{i_1}| ≤ OPT(S) + \sum_{i=1}^{k-1}overlap(s_{i_1}, s_{i+1_1})$
となります。

よって、$\sum_{i=1}^{k-1}overlap(s_{i_1}, s_{i+1_1}) \leq 2OPT(S)$ を示せばよいことになります。

最小閉路被覆の最適な閉路集合中の2つの閉路 $c_p$, $c_q$ と、
それぞれの閉路中の任意の頂点に対応した文字列 $s_p$, $s_q$ を考えます。
すると $|overlap(s_p, s_q)| \leq w(c_p) + w(c_q)$ が成り立ちます。
証明の詳細は割愛しますが、アイデアだけを以下に書きます。

背理法の仮定として $|overlap(s_p, s_q)| > w(c_p) + w(c_q)$ を仮定します。
この不等式は、異なる閉路の頂点同士を結ぶ辺の重みがとても小さいということを意味します。
（overlap が大きいということは、pref が短くなり、辺重みも小さい）
そのことが結果として、最小閉路被覆であることに矛盾します。

したがって、
$\sum_{i=1}^{k-1}overlap(s_{i_1}, s_{i+1_1}) \leq
\sum_{i=1}^{k-1}(w(c_{i_1})+w(c_{i+1_1})) \leq 2CCP(S) \leq 2OPT(S)$
となり、証明は完了です。

まとめ

全体的に不親切な内容になってしまいましたが、
最短超文字列問題に対する4近似アルゴリズムを紹介しました。

私の文章力不足のために近似率の解析がややこしくなってしまいましたが、
アルゴリズムの考え方自体はとてもシンプルでしたね。
最短超文字列問題を、プレフィックスグラフ上の最小閉路被覆問題に帰着することで、
多項式時間で最適解の4倍以下の近似解を求めることができました。
ちなみにこのアルゴリズムは、もうちょっとだけ工夫すれば、3近似にすることもできます。
気になる方は参考文献を読んでみてください。

また、最短超文字列問題は、ナイーブな貪欲アルゴリズムで
近似率 $2$ が達成されると予想されていますが、その真偽は証明されていません。
近似アルゴリズム、なかなか奥が深そうです...

これからの人生で NP 困難問題に直面したときは、
近似アルゴリズムを考えてみるのも面白いかもしれませんね。

参考文献

[1] BLUM, Avrim, et al. Linear approximation of shortest superstrings. Journal of the ACM (JACM), 1994, 41.4: 630-647.
[2] V.V.ヴァジラーニ (著),‎ 浅野 孝夫 (訳). 近似アルゴリズム. 丸善出版, 2012.

1. 英語では "Shortest Superstring Problem" です。「最短拡大文字列問題」という訳もよく見ます。 ↩

2. 厳密には、最短超文字列問題を判定問題に書き換えた問題が NP 困難です。 ↩

3. 置換と書きましたが、要は文字列の並び替えです。オーバーラップの合計が最も大きくなるような並び替えを考える、ということです。 ↩

4. 英語では "Cycle Cover Problem" などと言われています。 ↩

5. 巡回セールスマン問題は英語で "Traveling Salesman Problem" です。 ↩

6. 巡回セールスマン問題の解は最小閉路被覆問題の解にもなるので、$CCP(S) > TSP(S)$ と仮定すると $CCP(S)$ の最小性に矛盾します。 ↩