Range Minimum Query

この記事は「文字列アルゴリズム Advent Calendar 2016」22日目の記事です．

はじめに

この記事では，Range Minimum Query (RmQ) という問題を扱います．
RmQ は数列に対する基本的かつ重要な問題の1つであり，文字列に関する問題を解くときにも部分問題として頻繁に登場します．このことから，RmQ は文字列アルゴリズムを学ぶ上で欠かせない存在であると言ってもよいでしょう．この記事ではそんな RmQ を解くためのアルゴリズムの1つを紹介していきます．

もし致命的な間違いがあった場合は，コメントなどでご指摘いただけると幸いです．

Range Minimum Query (RmQ)

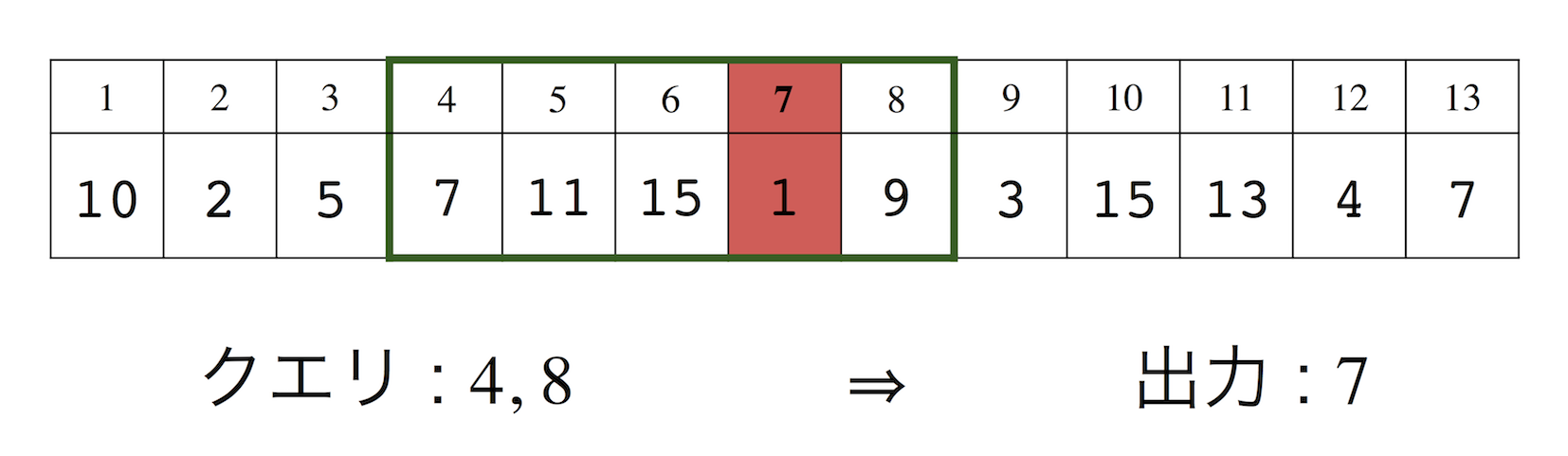
Range Minimum Query (以下 RmQ) は次のような問題です．

事前入力 : 長さ $n$ の整数列 $A[1..n]$.
クエリ入力 : 整数 $i, j, (1 ≤ i ≤ j ≤ n)$．
出力 : 部分整数列 $A[i..j]$ 中の最小値の位置 ($RmQ(i,j)$ であらわす)．

図1 : RmQ の例

RmQ を解くためのアルゴリズムは，様々なものが考案されています．
2000年，Bender と Farach-Colton [1] は RmQ を前処理時間 $O(n)$，クエリ時間 $O(1)$ で解くアルゴリズムを提案しました．さらに 2002年，Alstrup ら [2] は Bender, Farach-Colton のアルゴリズムの一部を変更したアルゴリズム¹を提案しました．この記事では後者，Alstrup ら [2] のアルゴリズムを紹介します．

まず最初に，前処理が 線形時間ではない アルゴリズムを紹介します．

Sparse Table algorithm

ここでは， Sparse Table algorithm と呼ばれるアルゴリズムを紹介します．このアルゴリズムは前処理時間 $O(n\log n)$ ，クエリ時間 $O(1)$ を達成します．

Sparse Table algorithm のアイデアをひとことで言うと，「各位置から始まる長さが2のべき乗 （1, 2, 4, 8, ...） の部分整数列に対して， RmQ の答えを事前に計算して表に記録しておこう！」です．

具体的には，前処理として以下をみたす表 $ST[1..n][0..\lfloor\log_2n\rfloor]$ を作成します．

ST[i][p] = RmQ(i, \min \{i+2^p-1, n\})

$ST$ は以下の漸化式を用いた DP により $O(n\log n)$ 時間で計算可能です．

ST[i][p] = 
\left\{
  \begin{array}{l}
    i \quad & \mbox{if }\,p = 0.\\
    \arg\min\{A[ST[i][p-1]], A[ST[q][p-1]]\} \quad & \mbox{otherwise.}
  \end{array}
\right.\\
\text{where}\quad q = \min \{ i+2^{p-1}, n \}

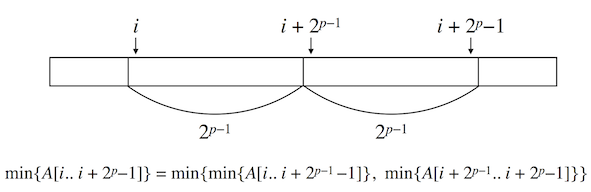
図2 : Sparse Table algorithm の漸化式のイメージ

クエリ $i, j$ に対しては， 表 $ST$ の高々2ヶ所を参照して数列の値を比較すれば十分です．
式で書くと以下のようになります²．

RmQ(i,j)=\arg\min\{A[ST[i][k]], A[ST[j-2^k+1][k]\}\quad
\text{where}\quad k = \lfloor\log_2(j-i)\rfloor

$A[i..j]$ 中の最小値が欲しかったら $A[i..x]$ 中の最小値と $A[y..j]$ 中の最小値を比べればいいよね！ ($i \leq y \leq x \leq j$) ってことです.
なお，ここでは $\lfloor\log_2(x)\rfloor$ を定数時間で計算できると仮定しています．これは $x$ のビット表現において $\mathsf{1}$ が立っている最上位のビット (Most Significant Bit) の位置を求める演算と同値であり，理論的に定数時間で可能です．詳細はこちらの記事をご参照ください．

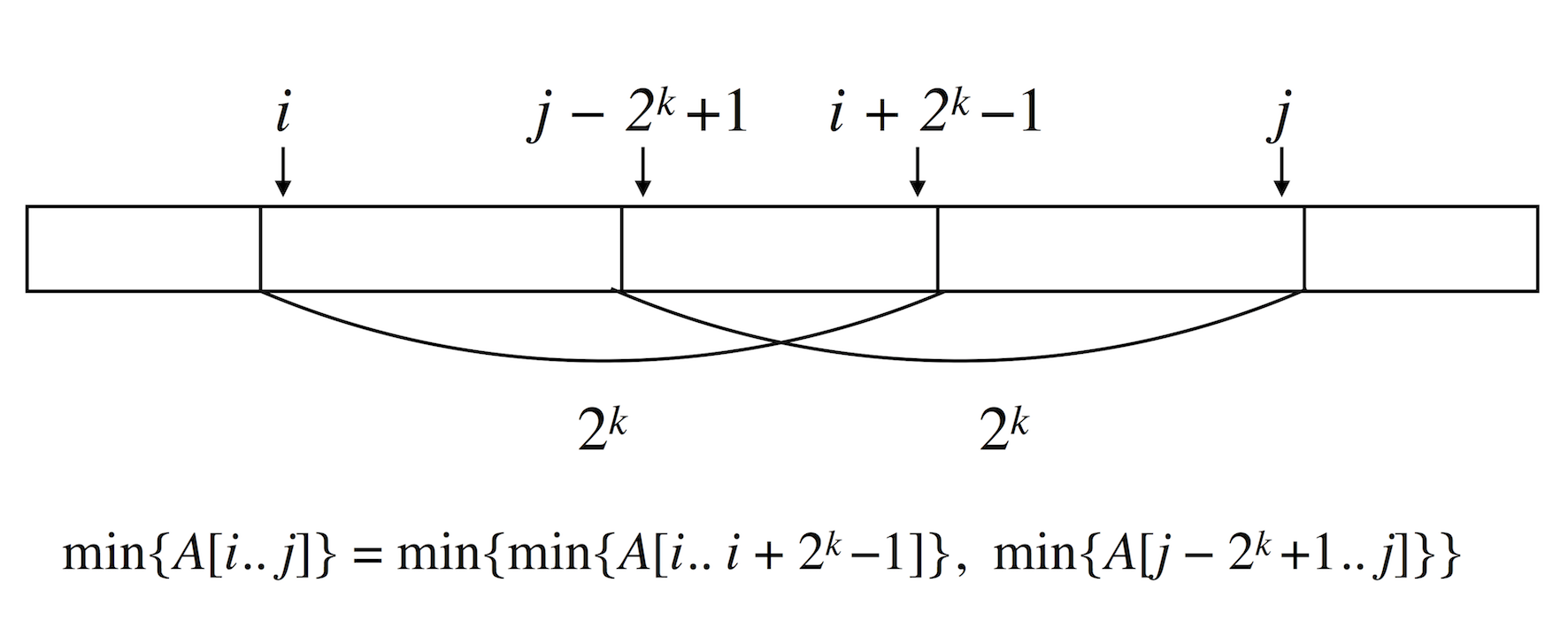
図3 : Sparse Table algorithm のクエリのイメージ

このアルゴリズムの面白い点は，クエリの種類は $O(n^2)$ 種類存在するにも関わらず，事前に計算して記憶しておく答えの数は $O(n\log n)$ 個でよいというところだと思います．

ポイントは，答えを覚えておく区間の長さを2のべき乗ずつ増やしながら，間をすっとばしている点です．これにより，$O(n\log n)$ 種類の答えを覚えるだけで定数時間クエリ応答を達成しています．

メインのアルゴリズムのアイデア

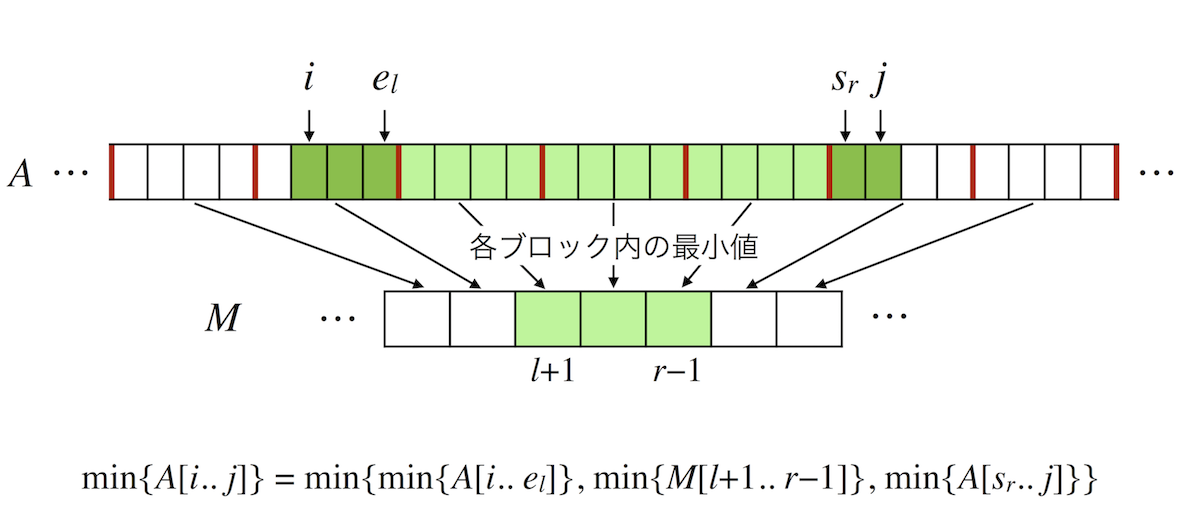
さて，本題の前処理時間 $O(n)$ のアルゴリズムの説明に入っていきます．まず，入力の長さ $n$ の整数列 $A$ を，長さ $m := \lfloor\frac{\log_2n}{2}\rfloor$ のブロックに分割することを考えます³.そして各ブロック内の最小値を格納した配列 $M$ を作成しておきます．すると，クエリ $i, j$ がそれぞれ異なるブロックに属する場合の $RmQ(i,j)$ の値は

• $A[i..e_l]$ 中の最小値
• $M[l+1..r-1]$ 中の最小値
• $A[s_r..j]$ 中の最小値

の3つを比較すればわかります⁴．
ここで $l, r$ はそれぞれ $i,j$ が属するブロックの番号を表し，$s_q, e_q$ はそれぞれ $q$ 番目のブロックの開始，終了位置を表すとします．

図4 : 全体のクエリのイメージ

つまり，各ブロック内の RmQ と $M$ 上の RmQ にそれぞれ定数時間で答えることができれば，$A$ 上の RmQ に定数時間で答えることができるというわけです．
では目標の計算量を達成するために，$M$ 上およびブロック内でどのように RmQ に答えるのかを考えていきましょう．

M 上の RmQ

$M$ 上の RmQ については，$M$ に対して Sparse Table algorithm を適用させるだけです．配列 $M$ のサイズを $k$ とすると，この部分の前処理時間は $O(k\log k)$ です．ここで，$k = \lceil \frac{n}{m} \rceil \in O(\frac{n}{\log n})$ だったので $O(k\log k) = O(\frac{n}{\log n} \log\frac{n}{\log n}) \subset O(n)$ となり，前処理時間は $O(n)$ を達成しています．クエリ時間は前述の通り $O(1)$ です．

ブロック内の RmQ

ブロック内の RmQ では，ワード内のビット演算に基づくテクニックを使います⁵．このブロック内 RmQ が，Alstrup ら [2] のアルゴリズムにおけるオリジナリティのある部分になります．

前処理

ここでは，$A$ 中のブロックの1つに注目しましょう，そして，いま注目しているブロック（つまリ $A$ の部分整数列） を $B[1..m]$ で表すものとします，

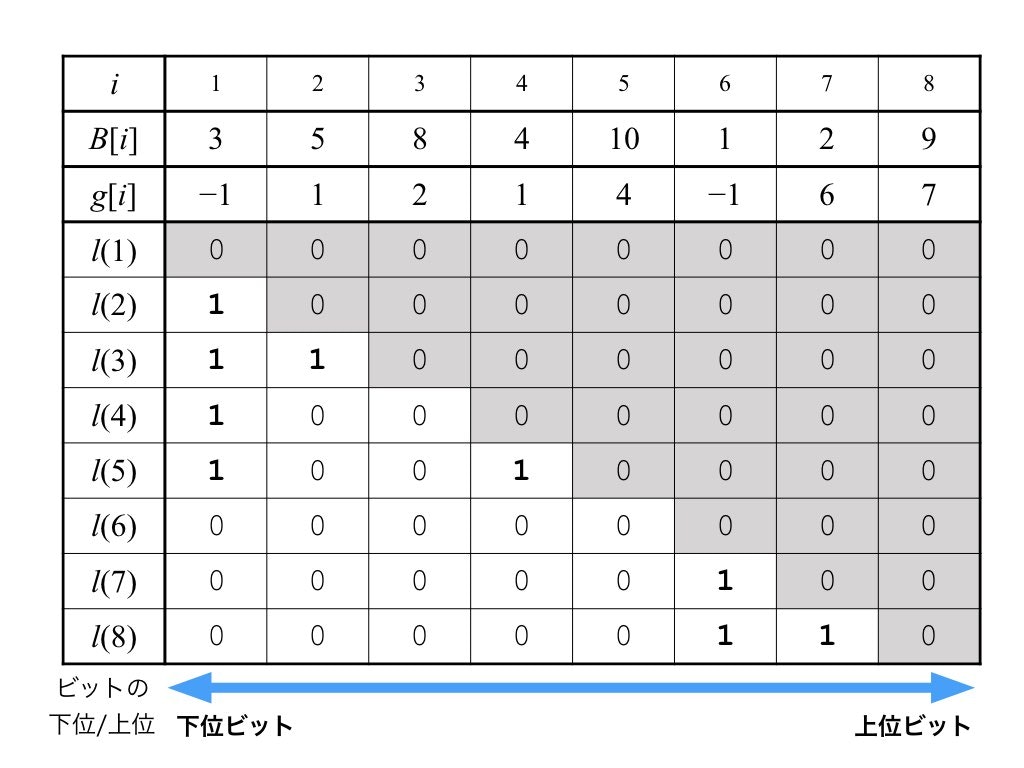
前処理では $B$ に対して，$m$ 個のビット列 $l(1), l(2), \cdots , l(m)$ を準備します．また，$l(j)$ の （最下位ビットから数えて） $i$ 番目のビットを $l(j)[i]$ と表すことにします．

各 $l(j)$ は，以下の条件を満たす長さ $m$ のビット列です:

$l(j)[i] = \mathtt{1}$ のときかつそのときに限り $B[i..j]$ の最小値が $B[i]$ である．

$l(j)$ は，ブロック内の位置 $j$ で終わる区間に対する RmQ の答えの情報を保持したビット列と考えることができます．下図に具体例を示します．下図のビット列は左が下位ビットで右が上位ビットであることに注意してください．

図5. ビット列と $g$ の具体例

次に，ビット列 $l(j)$ を計算する方法を考えましょう．各ビット列 $l(j)$ を効率的に計算するために，以下のような配列 $g[1.. m]$ を考えます．

g[i] = \max\{ p \mid p < i,\, B[p] < B[i]\}\cup\{-1\}

つまり $g[i]$ には，$B[1..i]$ 中で $B[i]$ 未満の値をとる位置のうち $i$ に最も近い位置が格納されています(もしそのような位置がなければ -1)．このように $g$ を定義をすると，$q \geq 2$ のとき

l(q) = l(g[q])\,|\,(1<<(g[q]-1))

が成り立ちます(ただし $g[q] = -1$ のときは特別に $l(q) = 0$ とします)．つまり，$l(i)$ は $l(g(q))$ をコピーしてさらに $g(q)$ ビット目に $\mathtt{1}$ を立てたものと言えます．また，$l(1) = 0$ と定義します．

よって，もし 配列 $g$ があれば，$m$ 個のビット列 $l(1), l(2), ..., l(m)$ すべてを $O(m)$ 時間で計算可能です．

また，配列 $g$ は $O(m)$ 時間で計算可能です（ここでは詳細を割愛しますが，気になる方はこちらの記事をご参照ください）．よって，ブロック $B[1..m]$ に対する前処理時間の合計は $O(m)$ であることが言えます．

クエリ

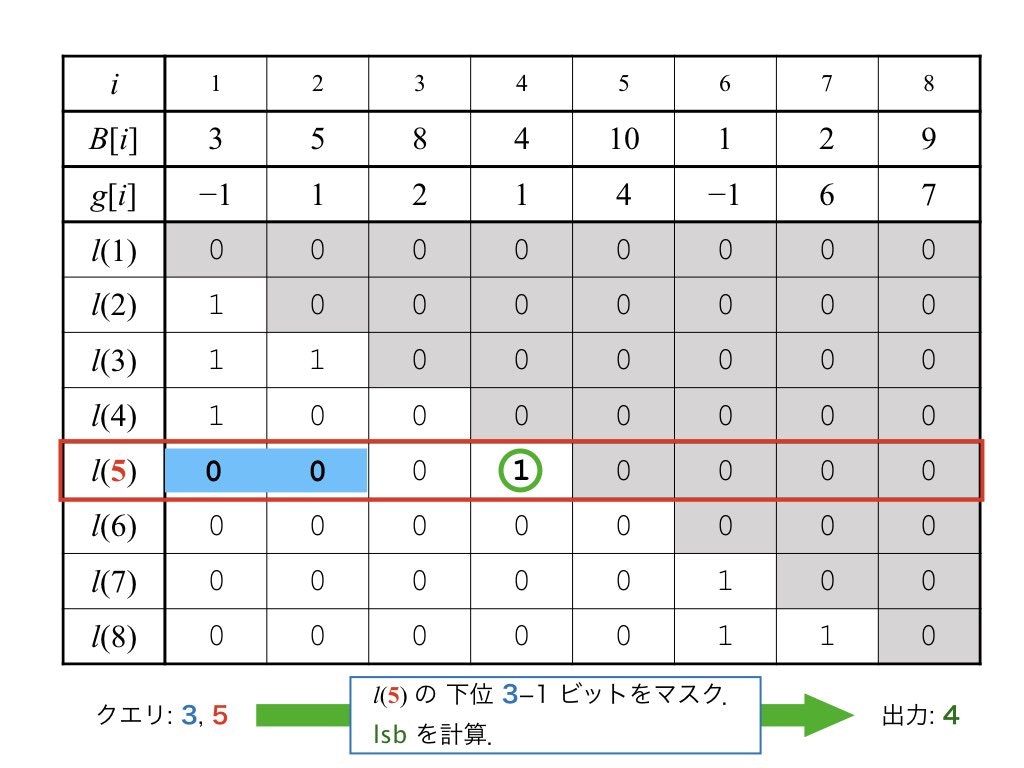
(ブロック内の)クエリ $i, j$ に対しては，$l(j)$ の下位 $i-1$ ビットを $\mathtt{0}$ でマスクした値 $w$ を考えます．

• $w = 0$ のとき
  $B[i.. j-1]$ 中に $B[j]$ より小さい値が存在しないということなので， $B[j]$ が答えになります．

• $w \neq 0$ のとき
  $w$ 中で1が立っているビットのうち最も下位のビットの位置が答えとなります． 「1が立っているビットのうち最も下位のビット」を least significant bit (lsb) と呼び， $w$ の lsb の位置を $\mathsf{lsb}(w)$ で表すことにします．この表記を用いると，$w \neq 0$ のときの答えは $B[\mathsf{lsb}(w)]$ ということになります．$\mathsf{lsb}(w)$ の値は $O(n)$ 時間の適当な前処理を行うと定数時間で計算可能です⁶．

よって，いずれの場合もクエリ時間 $O(1)$ が達成されています．

図6 : ブロック内 RmQ の例

まとめ

RmQ に対して前処理時間 $O(n)$，クエリ時間 $O(1)$ を達成するアルゴリズムを紹介しました．入力の整数列を長さ約 $\log n$ の部分整数列に分割して，Sparse Table algorithm (ブロック間 RmQ) とビット操作を用いたアルゴリズム (ブロック内 RmQ) を組み合わせるというものでした．LCA を用いた解法の方が広く知られているかと思いますが，こちらのほうが実装も楽でコードもコンパクトになるんじゃないかと思います．

(余談) RmQ/RMQ 記法について

今回の記事では，Range Minimum Query のことを RmQ と表記していました．中にはこの表記に違和感を感じられた方もいらっしゃったかもしれません．実際，今回参考にした文献[1]においては RMQ と表記していた上，他の多くの文献においても RMQ 表記が多く利用されています．

今回の RmQ という表記は文献[3]において登場しています．その理由は単純で，Range Minimum Query と Range Maximum Query の2つの問題を区別したかったのです．Range Minimum Query と Range Maximum Query の省略表記について，私は以下のようなものを見たことがあります．

Range Minimum Query	Range Maximum Query
RmQ	RMQ
rmq	rMq
RMin query	Rmax query

2番目の記法は小文字の r 始まりなことに私は違和感を感じます．
3番目の記法はわかりやすいですが単純にもっと短くしたいと思います．

というわけで，一番上の RmQ/RMQ 記法が最もしっくりきますよね！
みなさんも RmQ を利用する際は RmQ/RMQ 記法をぜひともご使用ください．私はもう RMQ という文字列を見たら Range Maximum Query にしか見えない体になってしまっています．いつの日か，このRmQ/RMQ 記法が世界の標準記法になる日が来ると信じています．

おわりに

Qiita で初めての投稿でした．こういう記事の執筆というのは，論文執筆やスライド作成とはまた違った難しさがあるように思います．駄文かつ長文を最後まで読んでいただいてありがとうございました．

参考文献

[1] Michael A. Bender and Martin Farach-Colton. The LCA Problem Revisited. In Proc. LATIN 2000, pp.88−94, 2000.
[2] Stephen Alstrup, Cyril Gavoille, Haim Kaplan and Theis Rauhe, Nearest Common Ancestors: A Survey and a New Distributed Algorithm. In Proc. 14th annual ACM symposium on Parallel algorithms and architectures, pp.258–264, 2002.
[3] Takuya Mieno, Shunsuke Inenaga, Hideo Bannai and Masayuki Takeda. Shortest Unique Substring Queries on Run-Length Encoded Strings. In Proc. MFCS 2016, pp.69:1−69:11, 2016.

1. Bender, Farach-Colton [1] のアルゴリズムは Lowest Common Ancestor (LCA) と RmQ の関係を用いたものでしたが，Alstrup ら [2] のアルゴリズムは LCA を利用しておらず，アルゴリズム全体がより短く簡潔になっています．なお，アルゴリズムの時間・領域計算量のオーダーについては， [1], [2] の間に違いはありません． ↩

2. $i = j$ の場合の解は明らかに $i$ であるので，ここでは $i < j$ の場合のみ考えます． ↩

3. 往々にして，$n$ は $m$ で割り切れないことがありますが，末尾のブロックの長さが $m$ 未満になるだけで本質的に問題ではありません． ↩

4. $i, j$ が同じブロックに属する場合は，そのブロック内の RmQ を求めるだけでよいです． ↩

5. その道の人のために補足すると，本記事では Word RAM model を仮定しています．即ち，1ワード内の基本的なビット演算（ビットシフトなど）が定数時間で実行できると仮定しています． ↩

6. lsb を事前に計算して表に記録しておく方法や，複雑なビット演算を利用する方法が考えられます．後者に関しては，MSB (Most Significant Bit） についての記事が Qiita に投稿されているのでそちらが参考になります．Most と Least の違いはありますが，本質的には同じです．実装する場合は，例えば GCC ならば __builtin_clz などの builtin 関数を用いると効率的です． ↩