はじめに

Qiitaデビューです．@kampersandaです．

この記事では，さまざまな文字列処理アルゴリズムの理論的基礎となっている決定性有限オートマトン（以下，オートマトンと書きます）をダブル配列により表現する方法を紹介します．この記事で紹介する手法は以下の論文で提案されているものです．

前田敦司, 水島宏太. オートマトンの圧縮配列表現と言語処理系への応用. プログラミングシンポジウム, pp. 49–54, 2008.

まずダブル配列について簡単に説明しますと，ダブル配列とはトライと呼ばれるラベル付き木を表現するためのデータ構造の一つです．検索が非常に高速であり，形態素解析器MeCabの辞書引きなどに用いられています．トライのダブル配列表現についての解説はブログや書籍などで多く拝見されます．Wikipediaのトライ木にも説明が載っています．一方で，実はオートマトンも表現できるということはあまり知られていないと思います．（個人の見解です）

この記事ではトライのダブル配列表現を知らなくてもわかるように書くつもりですが，知っているほうが理解し易いと思います．もしこの機会にトライのダブル配列表現も知ろうを思われた方には，情報系修士にもわかるダブル配列などの記事がおすすめです．

オートマトン

本記事では，オートマトンを5個組 $(Q, \Sigma, \delta, q_0, F)$ として定義します．ここで，

$Q$ は状態の有限集合
$\Sigma$ は入力文字の有限集合
$\delta:Q \times \Sigma \rightarrow Q$ は遷移関数
$q_0 \in Q$ は開始状態
$F \subset Q$ は受理状態の有限集合

です．ただし $\delta(q, c) = nil$ は $\delta(q, c) \not\in Q$ で，入力文字は $\Sigma = \{0,1,...,|\Sigma| - 1\}$ の整数として扱われます．

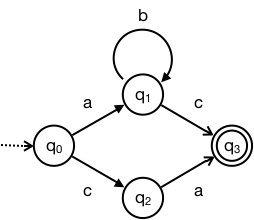
例として以下に $\{ \texttt{ab*c}, \texttt{ca}\}$ を認識するオートマトンを示します．

このオートマトンでは，$Q = \{q_0, q_1, q_2, q_3\}$，$\Sigma = \{\texttt{a}, \texttt{b}, \texttt{c}\}$，$q_0$ は開始状態，$F = \{q_3\}$ で，$\delta$ は

	$\texttt{a}$	$\texttt{b}$	$\texttt{c}$
$q_0$	$q_1$	$nil$	$q_2$
$q_1$	$nil$	$q_1$	$q_3$
$q_2$	$q_3$	$nil$	$nil$
$q_3$	$nil$	$nil$	$nil$

です．

オートマトンを表現するとは，この遷移関数 $\delta$ をいかにして計算機上に実装するかということです．その最も簡単な方法は，上記した表のような各要素が遷移先状態を保持した $|Q| \times |\Sigma|$ のテーブル（状態遷移表って呼ばれたりします）を用いる方法です．このテーブルを仮に $T$ としたとき，$\delta(q,c) = T[q][c]$ です．

一方で，このテーブルのメモリ使用量は $\Theta(|Q| \cdot |\Sigma|)$ と結構大きいわけでして，見て分かる通り結構な数の要素が $nil$ です．このような $nil$ の表現にわざわざ要素を割り当てずに，切り詰めて遷移関数 $\delta$ が実装できればメモリ効率よくオートマトンが表現できそうです．そしてそれを叶えるのがみんな大好きダブル配列です．

オートマトンのダブル配列表現

オートマトンを表現するためのダブル配列では，$Next$ と $Check$ という２つの配列を用います．$Next$ と $Check$ は同じ長さの配列で，各要素が遷移¹に対応しています．すなわち，これら配列の添字が遷移にIDを与えています．また，状態に対してもそれとは別に整数値のIDが割り当てられます．

$Next$ と $Check$ の役割について，ID $t$ の遷移に対して $Check[t]$ は遷移文字を保持し，$Next[t]$ は遷移先状態のIDを保持します．これらの配列を用いて，以下の式を満たすように状態と遷移のIDを定義することでオートマトンは表現されます．

\delta(q,c) = \left\{
\begin{array}{ll}
Next[q + c] & (if ~ Check[q + c] = c) \\
nil & (otherwise)
\end{array}
\right.

ただし，すべての状態IDが他の状態IDと重複しておらず，すべての遷移IDが他の遷移IDと重複していないことを前提とします．（まぁIDってそもそもそういうものですが...）

この式について説明します．遷移関数 $\delta$ が受け取った状態 $q$ から出る遷移のID候補は，その状態IDと入力文字の和によって求められます．すなわち，$t = q + c$ がこの遷移のID候補になります²．そして，この遷移先が存在するかどうかは $Check[t]$ によって確認でき，$Check[t] = c$ のとき $\delta(q, c) \neq nil$ であることが確認されます．$\delta(q, c) \neq nil$ であるとき，この遷移のIDは $t$ であり遷移先状態のIDは $Next[t]$ によって得ることができます．

ダブル配列による $\delta$ の実装をPythonで書くと以下のようになります．

def delta(q, c):
    t = q + c
    if Check[t] == c:
        return Next[t]
    else:
        return -1 #nil

このコードからもわかるように，ダブル配列表現では $\delta$ をこれだけ少ない演算回数で実行することができます．とても素敵です．

構築例

では，この条件式を満たすような状態IDと遷移IDはどのように決定すればいいのでしょうか．ここでは上に例示したオートマトンに対し $Next$ と $Check$ を構築する様子を追うことで，IDを決定する手順を説明したいと思います．ちなみに各文字の値は $\texttt{a} = 0$，$\texttt{b} = 1$，$\texttt{c} = 2$ です．

まず，この構築は開始状態 $q_0$ に対する状態IDを決めることから始まります．ここで注意していただきたいのが，条件式からも分かる通り状態 $q$ から出る遷移のIDは $q + c$ によって自動的に決まるということです．すなわち，$q_0$ に対する状態IDに文字 a または文字 c を足した値が，それぞれの遷移IDとして定義されるということです．そのため，そうして決まる遷移IDが他の遷移IDと重複しないように $q_0$ の状態IDを決める必要があります．

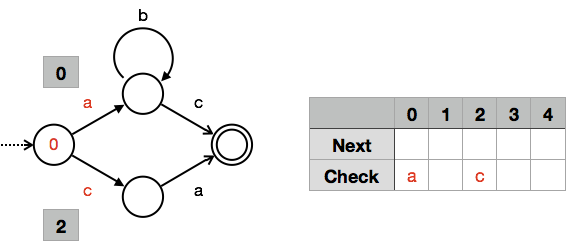
といってもまだ何の遷移IDも定義されていないため，とりあえず $q_0$ の状態IDは 0 とします．文字 $\texttt{a}$ と文字 $\texttt{c}$ による遷移のIDはそれぞれ自動的に $0 + \texttt{a} = 0 + 0 = 0$，$0 + \texttt{c} = 0 + 2 = 2$ というふうに決まります．遷移IDが決まったので，それぞれの遷移を識別するために $Check[0] = \texttt{a}$，$Check[2] = \texttt{c}$ を設定します．ここまでの経過を図示したのが以下になります．

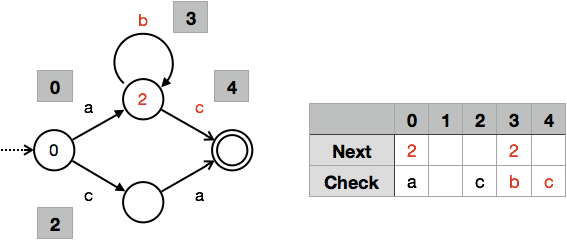
続いて状態 $q_1$ のIDを決定します．ここでも先ほどと同じように $q_1$ から出る遷移のIDが衝突しないように状態IDを決定します．このとき状態IDが他の状態IDとも被らないように決定します．ここでは状態IDに 2 を選べば，$2 + \texttt{b} = 2 + 1 = 3$，$2 + \texttt{c} = 2 + 2 = 4$ となり遷移IDが衝突しません．状態IDが決まったので，遷移 0 が状態 2 を指し示すことを $Next[0] = 2$ に記述し，先ほどと同様 $Check[3] = \texttt{b}$，$Check[4] = \texttt{c}$ を設定します．また，遷移 3 が指し示す状態IDは 2 とわかっているので，$Next[3] = 2$ を設定します．ここまでの経過を図示したのが以下になります．

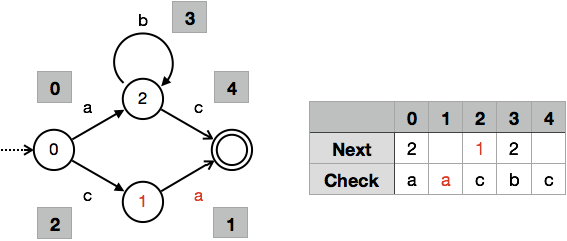
ここからの説明は若干くどい気もしますが，状態 $q_2$ のIDの決定を考えます．ここでは状態IDに 1 を選べば，$1 + \texttt{a} = 1 + 0 = 1$ となり，状態IDも遷移IDも衝突しません．前のステップと同じように $Next[2] = 1$ を設定し，$Check[1] = \texttt{a}$ を設定します．ここまでの経過を図示したのが以下になります．

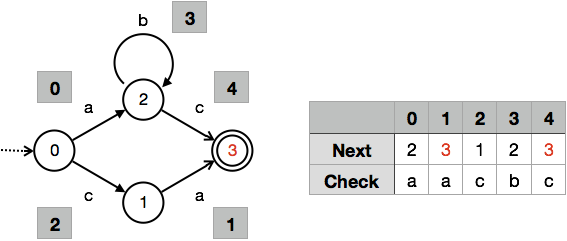
最後に状態 $q_3$ のIDを決定しますが，この状態から出る遷移は存在しないので，状態IDが衝突しないことだけに注意すればよいです．ここではとりあえず 3 に決定し，それに応じて $Next[1] = 3$，$Next[4] = 3$ を設定します．こうして以下のダブル配列表現が完成します．

この例ではノータッチでしたが，受理状態を示す $Next$ を負値としておくなどの方法で受理状態か否かを簡単に識別することができます．この例では $Next[1] = -3$，$Next[4] = -3$ となります．

遷移例

せっかくダブル配列が完成したので，きちんと遷移ができるかを確認してみたいと思います．

$\delta(0,\texttt{c}) = 1$
- 状態 0 と文字 $\texttt{c}$ の和により遷移のID候補 $0 + 2 = 2$ を算出します．
- この遷移が定義されていることは $Check[2] = \texttt{c}$ により確認できます．
- 次の状態IDは $Next[2] = 1$ により得られます．
$\delta(2,\texttt{b}) = 2$
- 状態 2 と文字 $\texttt{b}$ の和により遷移のID候補 $2 + 1 = 3$ を算出します．
- この遷移が定義されていることは $Check[3] = \texttt{b}$ により確認できます．
- 次の状態IDは $Next[3] = 2$ により得られます．
$\delta(1,\texttt{b}) = nil$
- 状態 1 と文字 $\texttt{b}$ の和により遷移のID候補 $1 + 1 = 2$ を算出します．
- しかし $Check[2] = \texttt{c}$ で遷移文字 $\texttt{b}$ と一致しないので，遷移先が存在しないことがわかります．

ちゃんと表現できてるようでよかったです．

おわりに

というわけで終わりです．この記事ではトライの表現法として親しまれるダブル配列でオートマトンを表現する方法を紹介しました．高速なオートマトンを実装したい人には是非おすすめの手法です．本当はもっと原理的なことも説明できたらよかったのですが，ちょっと文量が多くなりすぎるのでスキップしました．その辺りにも興味がある方は「はじめに」で紹介した論文を読んでみてください．

実はオートマトンのダブル配列表現についてはこれ以外にも随分と前に提案されています³．ですが今回紹介した表現のほうがメモリ効率が良いです．また，今回の手法とは違うアプローチでDAWGをダブル配列により表現する手法も提案されています⁴．この論文ではDAWGをダブル配列でも表現できる形に変形するアプローチを提案しており，Darts-cloneの実装などで用いられています．また，これらの手法を比較した論文もあります⁵．気になる方はこれらの論文もおすすめです．

あと完全に宣伝ですが，ダブル配列ベースの圧縮トライ辞書ライブラリ「Xcdat」を公開しているのでどうぞよろしくお願いします．

以上です．

「遷移」という言葉がわかりづらいかもしれませんが，図で言うところの実線の矢印です．グラフで言うところの「辺」で，木で言うところの「枝」です． ↩
トライのダブル配列表現についてご存知の方はお気づきかもしれませんが，状態IDが従来のダブル配列におけるBASE値のような役割を果たしています． ↩
青江順一. ダブル配列による有限状態機械の効率的インプリメンテーション. 電子情報通信学会論文誌D J70-D(4): 653–662, 1987. ↩
Susumu Yata, Kazuhiro Morita, Masao Fuketa, and Jun-ichi Aoe. Fast string matching with space-efficient word graphs. In Proceedings of International Conference on Innovations in Information Technology, pp. 79–83, 2008. ↩
Masao Fuketa, Kazuhiro Morita, and Jun-ichi Aoe. Comparisons of efficient implementations for DAWG. International Journal of Computer Theory and Engineering 8(1): 48–52, 2016. ↩

ダブル配列で決定性有限オートマトンを表現する

はじめに

オートマトン

オートマトンのダブル配列表現

構築例

遷移例

おわりに