本記事は、「データ構造とアルゴリズム Advent Calendar 2018」 11日目の記事です。
10日目の記事は @Gaccho 氏による「完全ローグライクダンジョン生成アルゴリズム🚪」でした。
12日目の記事は @Gaccho 氏による「「アルゴリズムこうしん」のアルゴリズムを作成する」です。
本記事では、「最短包含区間問題」という問題についてお話します。
本記事には新しい概念や高度なテクニックは登場しないため、アルゴリズムを生業とされている皆様にはお楽しみいただけないかもしれませんが、どうぞ最後までお付き合いください。
問題定義
以下のような、区間集合に対する問題を考えます。なお特に断りがない限り、本記事に登場する数値はすべて正の整数値であるとします。
最短包含区間問題
事前入力: $[1 ..N]$上の、互いに包含関係のない(ネストしない)区間の集合 $I$
クエリ入力: $[1 ..N]$上の区間 $[s, t]$
出力: $I$ の要素のうち、$[s, t]$ を包含する最短の区間すべて(存在しない場合は $nil$)
以下では、事前入力の集合のサイズを $m$ (即ち $m := |I|$) とします。
例
$N = 9$
事前入力: $I = \{[1, 3], [3, 4], [5, 7], [6, 8], [9, 9]\}$
クエリ入力: $[6, 7]$
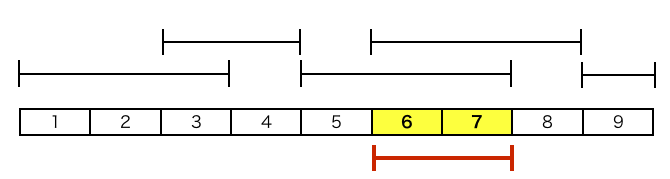
事前入力の区間(図の黒色の区間)のうち、クエリ入力の区間(図の赤色の区間) を含む区間は、$[5, 7], [6, 8]$ の2つです。そして、それらの区間の長さはどちらも $3$ です。よってこの例では、$[5, 7], [6, 8]$ の2つの区間が問題の出力となります(最短の区間は複数存在し得ることに注意)。
提案アルゴリズムの計算量
先に結論を述べますと、この問題は次の計算量で解くことができます。
前処理時間:$O(N)$ time
領域:$O(N)$ words
クエリ時間:$O(k+1)$ time1 ($k \geq 0$ は出力する解の個数)
以下では、上記の計算量を達成するアルゴリズムを紹介します。
解法
準備
アルゴリズムの説明の前に、いくつか準備をします。
まず、$I$ のサイズ $m$ についてですが、区間(整数の組)の集合なので最悪の場合 $N^2/2$ 程度になりそうな気がします。しかし本問題においては 「$I$ の要素は互いにネストしない」という仮定があるため、 $m \leq N$ が成立することがわかります。この事実は、計算量の解析に影響します。
次にアルゴリズムの方針ですが、以下の手順を踏むことで解を求めることができそうです。
クエリ入力 $[s, t]$ に対して、
- 事前入力の区間集合 $I$ から、$[s, t]$ を含む区間のみを取り出す。これを $I'$ とする。
- 区間集合 $I'$ の要素のうち、最短のものをすべて出力する2。
以下では、上記2ステップの効率的な実現方法を考えます。
アルゴリズム
直前に2ステップと言いましたが、準備も含めて3ステップに分けて説明します。
ステップ0: 3つの配列の準備
サイズ $m$ の3つの配列 $X[1..m], Y[1..m], L[1..m]$ を作成します。
まず、区間集合 $I$ の要素を開始位置について昇順にソートします。$I$ の要素は互いにネストしないという仮定なので、 区間を開始位置について昇順にソートすれば、終了位置についても昇順にソートされた状態になります。また、各位置の値は $N$ 以下であるため、バケットソートを用いることで $O(N)$ 時間でソート可能です3。
こうして昇順にソートした開始位置(resp. 終了位置)の列を、配列 $X[1..m]$ (resp. $Y[1..m]$) に格納します。さらに $X$, $Y$ を用いて、区間の長さを格納した配列 $L[1..m]$ を作成します。
ステップ1: クエリ入力の区間を含む区間の特定
"$[s, t]$ を含む区間" は、"開始位置が $s$ 以下かつ終了位置が $t$ 以上の区間" と言い換えることができます。そう考えると"$[s, t]$ を含む区間" の集合 $I'\subset I$ は、$X$ 上の $s$ の predecessor および $Y$ 上の $t$ の successor を用いて求めることができます。
s t
|--------|
|----- ← 解の候補
|----- ← 解の候補(最右)
|---- ← 解の候補ではない
s t
|--------|
--| ← 解の候補ではない
----| ←解の候補(最左)
----| ← 解の候補
predecessor/successor を求めるアルゴリズムについては、いくつかの手法が知られています。例えばデータ構造のサイズを $O(m)$ にしたい場合などは、y-fast trie を利用するとよいでしょう。なお、今回の目標は $O(N)$ 領域かつ定数クエリ時間であるので、「すべての位置に対する解を事前に求めて長さ $N$ の配列に格納しておく」というナイーブな手法をとります。
$X$ 上の $s$ の predecessor に対応するインデックスを $p$, $Y$ 上の $t$ の successor に対応するインデックスを $q$ とすると、解の候補 $I'$ は
$$I' = \{[X[q], Y[q]], [X[q+1], Y[q+1]], ..., [X[p], Y[p]]\}$$
にまで絞られます4。
なお、$I'$ はアルゴリズムの説明のために定義した集合であり、陽には計算しません($I'$ を保持しようとすると、最悪の場合 $O(N)$ 時間かかってしまいます)。実際は $p, q$ の値だけを求めて保持しておけば十分です。
=== 追記 ===
執筆当初、上記 $I'$ 内の $p$, $q$ を逆に書いてしまっていました。細かいところまで読み、ご指摘くださった @kgoto さん、 @m_funa さんありがとうございました。
=== 追記ここまで ===
ステップ2: 最短区間の特定
あとはステップ1で求めた $I'$ の中から、最短のものを見つければ完了です。ステップ0で作成した配列 $L$ に対して、部分配列 $L[q..p]$ の最小値(のインデックス)を求めればよいです。この問題はズバリ、 RmQ (Range Minimum Query) そのものです。RmQ は、$O(|L|)$ 時間の前処理を行うことで定数クエリ時間で解けることが知られています。
最短の区間は複数存在し得るのですが、探索区間を狭めながら RmQ を繰り返すことで、解の個数に線形な時間ですべての解を見つけることができます(難しい話ではないのですが、ここでは詳細は割愛します)。
※余談(宣伝)ですが、私は過去のアドベントカレンダーで RmQ に関する記事も執筆しておりますので、興味とお時間のある方はぜひご覧になってください。
アルゴリズムの計算量
$X, Y$ 上の predecessor/successor は、前述のナイーブな手法を用いると
$O(N)$ words, $O(N)$ preprocess time, $O(1)$ query time
で解くことができます。
$L$ 上の RmQ は、Bender, Farach-Colton の手法などを用いると
$O(m)$ words, $O(m)$ preprocess time, $O(1)$ query time
で解くことできます。
したがって、以下の結論(再掲)が導かれます。
前処理時間:$O(N)$ time
領域:$O(N)$ words
クエリ時間:$O(k+1)$ time ($k$ は出力する解の個数)
また、predecessor/successor および RmQ については簡潔データ構造の存在が知られており、それらを利用することで下記の計算量で解くこともできます。
前処理時間:$O(N)$ time
領域:$2N + 2m + o(N)$ bits
クエリ時間:$O(k+1)$ time ($k$ は出力する解の個数)
簡潔データ構造については、共立出版の「簡潔データ構造」が詳しいです。
おわりに
今回は「最短包含区間問題」という問題についてお話しました。
この問題をそのまま利用する機会はおそらくないと思いますが、この問題のように既存の「道具」を組み合わせるだけで効率よく解ける問題はたくさんあると思います。
本アドベントカレンダーなどを活用して手持ちの道具を増やし、アルゴリズムライフをエンジョイしましょう!