Weighted Ancestor Query

本記事は，「データ構造とアルゴリズム Advent Calendar 2021」 16日目の記事です．

はじめに

この記事では，重み付き祖先クエリ (Weighted Ancestor Query; 以下，WAQ) という問題を高速に解くアルゴリズムについて解説します．WAQ は，根→葉方向に単調増加な頂点重みがついた根付き木に対するクエリです．クエリとして頂点 $v$ としきい値 $k$ が与えれたとき，$v$ の祖先のうち重みが $k$ 以上の最も高い (つまり頂点深さが小さい) 頂点を返します．

本記事では，頂点数 $N$ の重み付き木に対して，$O(N)$ 時間の前処理後に WAQ に $O(\log\log N)$ 時間で応答可能な手法を紹介します．まずはアイディアの基本である，heavy-light decomposition を用いた $O(\log N)$ クエリ時間のアルゴリズムを紹介します．その後，既存の強い手法 (Level Ancestor Query, static y-fast trie) を組み合わせることで，クエリ時間を $O(\log\log N)$ に落とします．後半の $O(\log\log N)$ 時間はともかく，前半の $O(\log N)$ 時間の手法はとてもシンプルでわかりやすいかと思います．半分だけでも是非読んでいってください．

• キーワード: Weighted Ancestor Query; Level Ancestor Query; heavy-light decomposition (heavy-path decomposition); y-fast trie.

木・(単調) 重み付き木

本記事で登場する木はすべて根付き木であるとします．木の各頂点 $v$ に非負整数の重み $w(v)$ が付いた木を重み付き木と呼び，特に，根以外の各頂点 $v$ に対して，$w(v) > w(\mathsf{parent}(v))$ を満たす重み付き木を，単調重み付き木と呼びます．ここで $\mathsf{parent}(v)$ は $v$ の親頂点を表します．
本記事に出てくる重み付き木はすべて単調重み付き木であるので，以下，単に重み付き木と書いたらそれは単調重み付き木であるとします．さらに本記事では，頂点数 $N$ の重み付き木の各頂点 $v$ の重みについて，$w(v)\le N$ であるという仮定を置きます．
重み付き木の例を次の図 1 に示します．

図 1. 重み付き木の例です．根以外の各頂点に対して，親の重みが自身の重み未満であることが確認できます．図中の頂点 $v_1$ と $v_2$ に対して，それぞれ $\mathsf{WAQ}(v_1, 3)$ と $\mathsf{WAQ}(v_2, 6)$ が表す頂点を図中に示しています．

重み付き祖先クエリ (Weighted Ancestor Query; WAQ)

さて，ここからは WAQ の定義とそれを解くアルゴリズムを紹介します．

WAQ の定義

WAQ の定義は以下のとおりです:
事前入力： 頂点数 $N$ の重み付き木 $T$.
クエリ入力： $T$ 中の頂点 $v$ と整数値 $k \le w(v)$ のペア $(v, k)$．
出力： 重みが $k$ 以上である $v$ の最も高い祖先 (つまり，頂点深さが小さい祖先).

また，クエリ $(v, k)$ に対する WAQ の答えの頂点を $\mathsf{WAQ}(v, k)$ で表します．クエリの具体例を上の図 1 に示しています．

前処理 O(N) 時間 & クエリ O(log N) 時間アルゴリズム

まず，入力の木 $T$ に対して HL-分解 (heavy-light decomposition) [3] を適用します．
HL-分解については，Qiita 上に素晴らしい記事が存在するので，そちらに丸投げします．ポイントだけ抜き出すと，

• 木の HL-分解とは，辺集合をあるルールに従って重辺 (heavy-edge) と軽辺 (light-edge) を分割することである．
• 重辺のみからなる極大なパスを重パス (heavy-path) と呼ぶ．
• 木の任意のパス (根→葉方向) に対して，そのパス内の軽辺の数は $O(\log N)$ である．
• HL-分解は木のサイズに線形な時間で計算できる．

$T$ の各頂点は，自身が属する重パスへのポインタを保持しておきます．このポインタは HL-分解をしながら計算できます．
それぞれの重パスを1つの頂点に縮約した木を分解木 (decomposition tree) と呼び，$D(T)$ で表します．$D(T)$ の各頂点は $T$ のそれぞれの重パスに対応しています．さらに，$T$ 上任意の異なる2つの重パスに対して，その間に $T$ の辺が存在するとき，対応する $D(T)$ の2頂点間にも辺があるとします (言葉だとわかりにくいと思うので，下記図 2 の具体例をご覧ください)．また，$D(T)$ 上の各頂点 $u$ に対して，重み $x(u)$ を $u$ に対応する重パスの先頭頂点の重みと定義します．

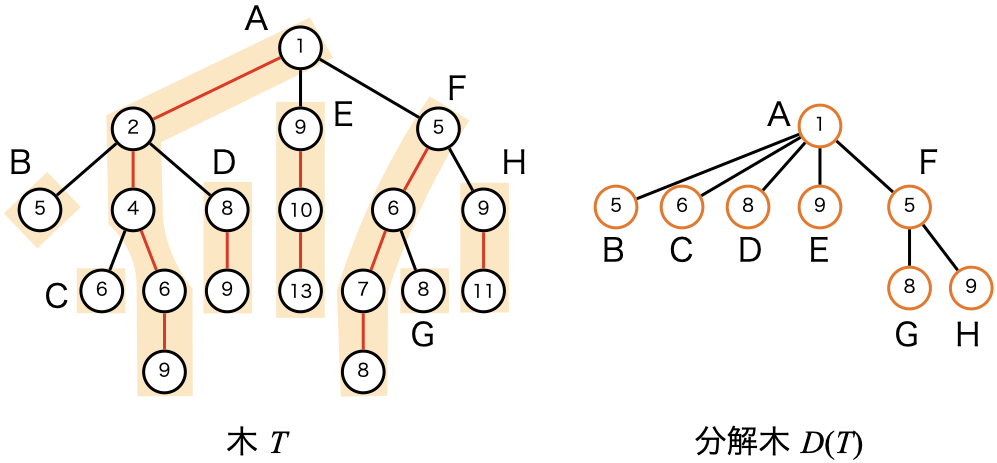図 2. HL-分解と分解木の具体例です．木 $T$ 中の重パスに A〜H の名前をつけており，それにより右の分解木の頂点との対応を表しています．分解木 $D(T)$ の頂点内には重パスの重みが書かれています．それらは，元の木 $T$ における重パスの開始頂点の重みとなっています．

クエリ $(v, k)$ に対して，頂点 $\mathsf{WAQ}(v, k)$ が属する重パスを求めたいときを考えます．このとき，まず $v$ が属する重パスに対応する $D(T)$ 上の頂点にジャンプして，そこから根方向に向かって線形探索を行うことで，分解木 $D(T)$ の高さに線形な時間で頂点 $\mathsf{WAQ}(v, k)$ が属する重パスを求めることができます．ここで，分解木 $D(T)$ の高さは $O(\log N)$ であることが知られているため，頂点 $\mathsf{WAQ}(v, k)$ が属する重パスは $O(\log N)$ 時間で求まることがわかります．

頂点 $\mathsf{WAQ}(v, k)$ が属する重パスがわかったあとは，その重パス内で，重みが $k$ 以上である最も高い頂点を求めればよいです．これは即ち重パス内での successor クエリであり，二分探索によって $O(\log N)$ 時間で具体的な頂点 $\mathsf{WAQ}(v, k)$ が求まります．

WAQ 前処理 O(N) 時間 & クエリ O(log log N) 時間アルゴリズム

先程のクエリアルゴリズムでは，
(1) $D(T)$ 上の WAQ に $O(\log N)$ 時間，
(2) 重パス内の二分探索に $O(\log N)$ 時間
をかけていました．ここからは，既存のデータ構造を利用することで，上記 (1), (2) の計算時間を $O(\log\log N)$ 時間に改善します．

(1) D(T) 上の WAQ

$D(T)$ の高さが $O(\log N)$ であるという性質を利用して，$D(T)$ 上の WAQ に $O(\log\log N)$ 時間に答える方法を与えます．ここでは，レベル祖先クエリ (Level Ancestor Query; 以下，LAQ) と呼ばれるクエリを利用します．定義は次の通りです．
事前入力： 頂点数 $N$ の木 $T$.
クエリ入力： $T$ 中の頂点 $v$ と整数値 $d$ (ただし，$v$ の深さ以下とする) のペア $(v, d)$.
出力： 深さが $d$ である $v$ の祖先.

LAQ は，各頂点の重みが頂点深さである場合の特殊な WAQ であると言えます．具体例を図 3 に示します．

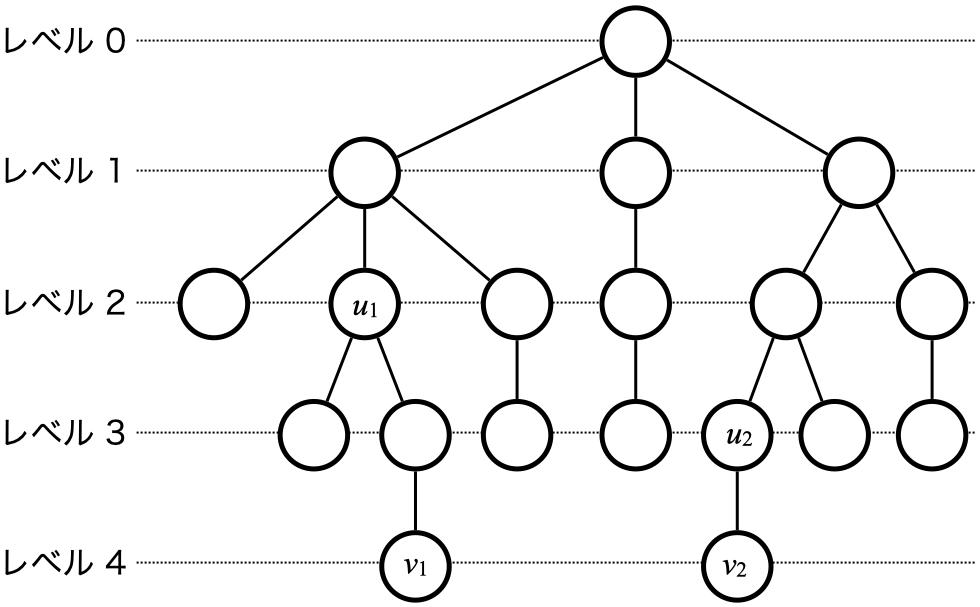図 3. LAQ の具体例です．根のレベル (深さ) を 0 とし，子の方向に進むごとにレベルは 1 だけ大きくなります．LAQ のクエリとして $(v_1, 2)$ が与えられたとき，$v_1$ の祖先のうちレベルが 2 である頂点 $u_2$ を返します．他のクエリとして $(v_2, 3)$ が与えられた場合，図中の $u_2$ を返します．

詳細は省略しますが，LAQ に対しては，$O(N)$ 時間の前処理の後，任意のクエリに $O(1)$ 時間で答えることができる手法が知られています [4, 5]．よって，LAQ と二分探索を組み合わせることで，$D(T)$ の高さに対して対数時間で WAQ に答えることができます．つまり，$D(T)$ 上の WAQ は $O(\log\log N)$ 時間で解くことができます．

(2) 重パス上の successor クエリ

頂点 $\mathsf{WAQ}(v, k)$ が属する重パスがわかれば，あとはその中の重み列に対する $k$ の successor を求めれば完了です．

Static y-fast trie

Successor (predecessor) といえば有名なデータ構造 y-fast trie があります [6]．これは長さ $m$ の単調な非負整数列に対する successor (predecessor) に $O(\log\log U)$ 時間で答えられる $O(m)$ 領域のデータ構造です．ここで $U$ は正整数の取りうる値の最大値です．ただし，オリジナルの y-fast trie は内部でハッシュを利用しており，構築時間 (もしくはクエリ時間) が期待時間になってしまいます．実用上は大きな問題ではないかもしれませんが，今回は決定的な時間で計算量を議論します．文献 [2] では，完全ハッシュ [7] を用いることで，
$U = O(m^c)$ の場合に $O(m)$ 時間で構築可能かつクエリに $O(\log\log U) = O(\log\log m)$ 時間で応答可能な静的 successor データ構造が存在することが示されました ($c$ は定数)．ここではそのデータ構造を static y-fast trie と呼ぶことにします．

すべての重パス上の successor クエリを 1 つの数列上の successor クエリへ帰着

決定的な successor データ構造に帰着するアイディアは以下のとおりです: すべての重パスの頂点重み列を連結した長さ $N$ の数列を作り，それに少し手を加えた上で static y-fast trie を構築します．
具体的な方法を述べます．重パス $p_i$ に対応する頂点重みの増加列を $s_i$ とします．$s_i$ の各要素に $(i-1)N$ を足した数列を $s'_i$ とします．すると，$s'_i$ の要素は $(i-1)N+1$ 以上，$iN$ 以下となります．$S$ を，$s'_1, s'_2, \ldots, s'_h$ の連結とします．$h$ は重パスの本数です．すると，$S$ は $\{0, 1, \ldots, hN\}$ 内の整数からなる長さ $N$ の増加列となります．いま $h \le N$ であるので，$S$ 上の successor に $O(\log\log N)$ 時間で答える static y-fast trie を $O(N)$ 時間で構築することができます．

頂点 $\mathsf{WAQ}(v, k)$ が属する重パスが $p_i$ であるとわかっているとき，$S$ 中で $k+(i-1)N$ の successor を求めることで，頂点 $\mathsf{WAQ}(v, k)$ を $O(\log\log N)$ 時間で求めることができます．

高速化のアイディアまとめ

さて，いろいろなデータ構造とアルゴリズムが出てきたので最後に全体像を整理しておきましょう．

前処理

1. 重み付き木に HL-分解を適用して，分解木 $D(T)$ を作成する．
2. 分解木 $D(T)$ に対して LAQ の前処理を行う．
3. 重パスの連結に対する数列 $S$ を作成し，$S$ に対する static y-fast trie を構築する．

クエリ処理

1. 分解木 $D(T)$ 上で LAQ を用いて二分探索を行い，答え頂点が属する重パスを求める．
2. 答え頂点が属する重パスの番号を元に，$S$ に対する successor によって答え頂点を求める．

以上より，$O(N)$ 時間前処理，$O(\log\log N)$ 時間クエリ応答が達成されます．

まとめ

重み付き祖先クエリ (Weighted Ancestor Query; WAQ) に $O(\log\log N)$ 時間で答えることができる手法を紹介しました．
また，本記事では $O(\log N)$ 時間で答えるシンプルな方法も紹介しています．前処理としては HL-分解がほぼすべてで，クエリ処理も線形探索と二分探索だけでした．実装派の方や競プロ勢の方にとっては，$O(\log N)$ 時間アルゴリズムの方が興味深いものだったかもしれません．

参考文献

重み付き祖先クエリ WAQ は文献 [1] において定義され，$O(N)$ 期待時間の前処理後にクエリに $O(\log\log N)$ 時間で答えるアルゴリズムが提案されました．本記事で紹介した内容は，前処理時間を決定的にした手法であり，文献 [2] にて紹介されています．
木に対する HL-分解は文献 [3] で提案されています．また，日本語での解説としては，Qiita 上でわかりやすい記事が公開されています: https://qiita.com/ageprocpp/items/8dfe768218da83314989.
レベル祖先クエリ (LAQ) の定数時間クエリアルゴリズムは，に対しては，文献 [4] で提案されました．さらに，そのアルゴリズムをよりシンプルにした結果が文献 [5] に記載されています．日本語での解説としては，いくつかの記事があります (下記参考文献参照)．
Successor/predecessor のための動的データ構造である y-fast trie は，文献 [6] にて提案されました．それを静的かつ決定的時間にする方法は文献 [2] に記載されています．日本語の解説としては，Qiita 上で非常に素晴らしい記事が公開されています: https://qiita.com/goonew/items/6ffac4b5e48dc05ca884.

日本語記事

• HL 分解の解説記事 (Qiita): https://qiita.com/ageprocpp/items/8dfe768218da83314989
• レベル祖先クエリの解説記事1: https://hdbn.hatenadiary.org/entry/20111125/1322194487
• レベル祖先クエリの解説記事2: https://37zigen.com/level-ancestor-problem/
• Y-fast trie の解説記事 (Qiita): https://qiita.com/goonew/items/6ffac4b5e48dc05ca884

論文

1. Farach, M., & Muthukrishnan, S. (1996, June). Perfect hashing for strings: Formalization and algorithms. In Annual Symposium on Combinatorial Pattern Matching (pp. 130-140). Springer, Berlin, Heidelberg.

2. Amir, A., Landau, G. M., Lewenstein, M., & Sokol, D. (2007). Dynamic text and static pattern matching. ACM Transactions on Algorithms (TALG), 3(2), 19-es.

3. Sleator, D. D., & Tarjan, R. E. (1983). A data structure for dynamic trees. Journal of computer and system sciences, 26(3), 362-391.

4. Berkman, O., & Vishkin, U. (1994). Finding level-ancestors in trees. Journal of computer and System Sciences, 48(2), 214-230.

5. Bender, M. A., & Farach-Colton, M. (2004). The level ancestor problem simplified. Theoretical Computer Science, 321(1), 5-12.

6. Willard, D. E. (1983). Log-logarithmic worst-case range queries are possible in space Θ(N). Information Processing Letters, 17(2), 81-84.

7. Alon, N., & Naor, M. (1996). Derandomization, witnesses for Boolean matrix multiplication and construction of perfect hash functions. Algorithmica, 16(4), 434-449.