Heavy-Light-Decomposition(日本語:HL分解)を知っていますか?
木に対する非常に有用なアルゴリズムですが、日本語の資料が非常に少ないです。めちゃくちゃ少ないです。あっても古いものばかりで、例も少ないです。
そこで、日本語のHL分解のわかりやすい記事がほしい!ということで、自分でこの記事を書いています。
名前だけ聞いたことがあるけどわからない…というような人がいたらぜひこの記事で理解してください。
木は更新に弱いという話
唐突ですが、木は状態の取得には強いですが、状態の変更にはかなり弱い構造です。
たとえば、次のような問題を考えてみましょう。
$N$ 頂点の重み付きの無向木が与えられる。
$Q$ 回、ある辺の重みを変更するクエリと、ある2つの頂点の間の距離を求めるクエリが与えられる。
これを、$1\leq N\leq 100000,1\leq Q\leq 100000$ で解け。
少し木について知っている人なら、この問題を見たとき少し解けるような気がしたかもしれません。
なぜなら、辺の重みの変更がなければ、この問題はLCA(最小共通祖先)を求めるアルゴリズムを使って、$O(N+Q\log N)$で解けるからです。LCAについては適宜調べてください。蟻本にも載っています。
しかし、辺の重みの変更によってこの問題の難しさは一気に上がります。
すべての頂点について根からの距離を保持するのがLCAを使った解き方の肝ですが、辺の重みの変更によってこれが崩れ落ちてしまうからです。
もう少し一般的に言うと、木へのクエリに対する高速な応答は、DFS/BFSなど、前処理で頂点ごとに情報を持っておくことに担保された部分が非常に大きいので、前処理が崩されると途端に弱くなってしまいます。
しかし、HL分解を使えば、更新にもクエリにも強い構造が構築できます。**これこそがHL分解が非常に便利な点です。**上の問題も解けます。
HL分解の強さはこれからじっくりと説明していきます。
なお、この問題はオイラーツアーとSegment Treeを使って解くこともできます。
列は更新とクエリに強いという話
唐突ですが、列は更新にも変更にも強い構造です。
Segment TreeやBITなどのデータ構造を使えば、区間和や区間最小/区間最大値の取得、区間更新や区間加算などのクエリが高速に処理できます。
Segment Treeの解説については、こちらをどうぞ。
木を列にしてしまえば最強だという話
上の話を見ておわかりになりましたでしょうか。
変更を加えても問題ない程度の大きさに木を圧縮して、変更は全部列に吸収させればいいのです。
さて、変更を加えても問題のなさそうな、つまり、前計算が崩れても高速処理が可能な木とはなんでしょうか。
そう、高さの低い木です。
たとえば平衡二分木のような木上なら、木のパスを愚直にたどっても高々 $O(\log N)$ 個のノードしか辿らず、そして、列に対するクエリには前に述べた通り $O(\log N)$で答えられます。
こうして、どんなクエリにも少なくとも $O(\log^2 N)$ で答えられることが分かりました。
つまり、木をなんとかして高さが $O(\log N)$ 以下の木に圧縮し、そのノードには列、つまり元の木のパスを持つようにしておけばクエリが高速に処理できます。
HL分解とは
さて、本題です。
HL分解は、木のパスをひとつのノードにまとめ、深さを高々 $O(\log N)$ にすることができるアルゴリズムです。
次のような木を例に考えます。
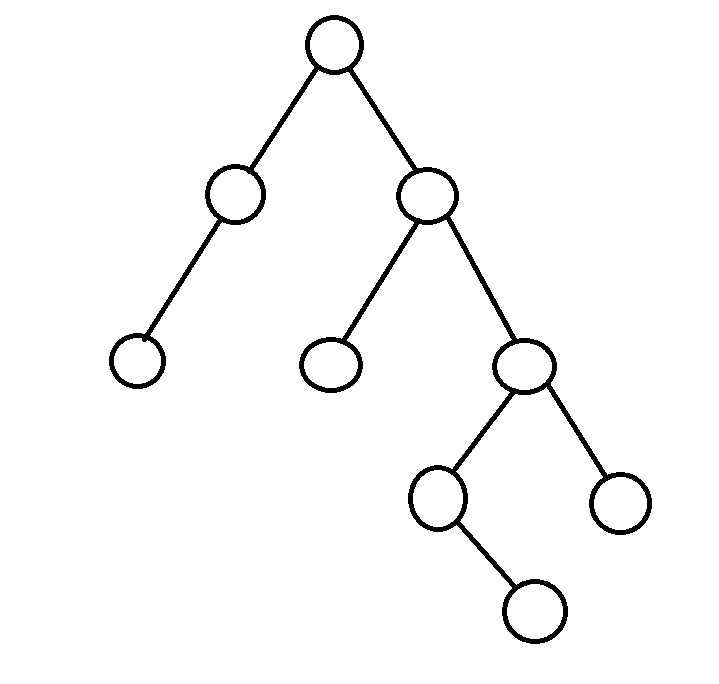
次のように、それぞれの頂点を根とする部分木のサイズをメモします。
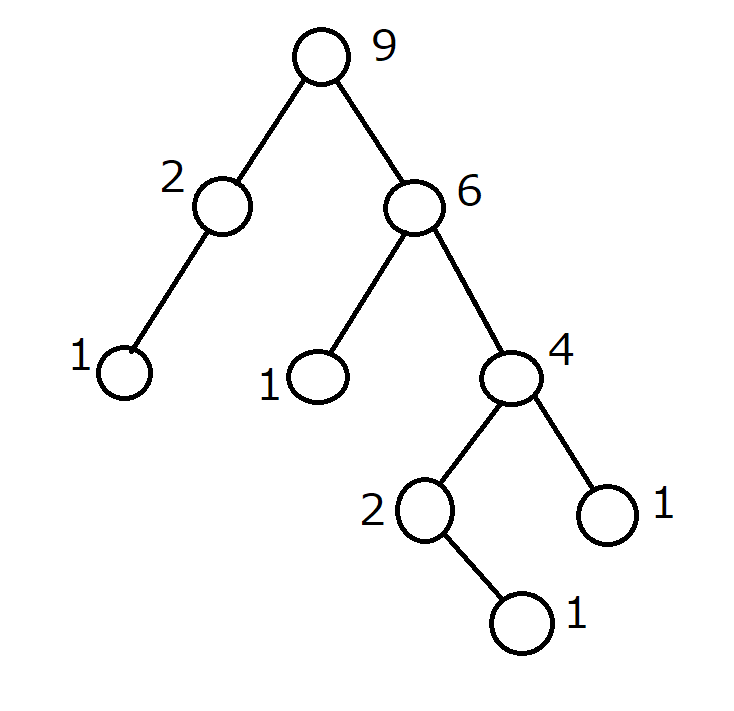
子のうち最もそれを根とする部分木のサイズが大きいものへの辺を、Heavyな辺とします。
サイズが最大のものが複数ある場合は、どれを選んでもいいです。
Heavyな辺は、次の図で赤く示したものです。
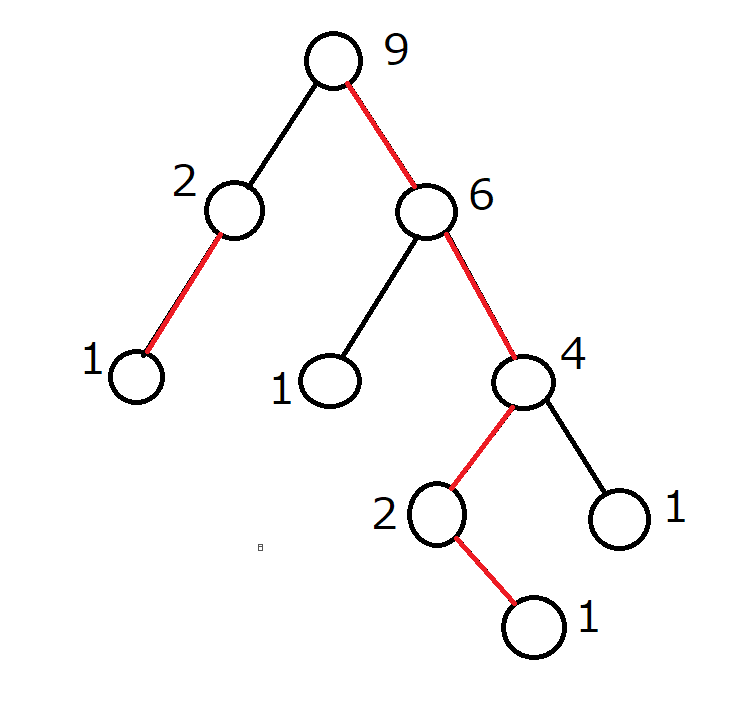
Heavyな辺は各頂点から高々1本しか出ていないので、Heavyな辺だけからなるパスは列になります。
Heavyな辺だけからなるパスをまとめてみます。
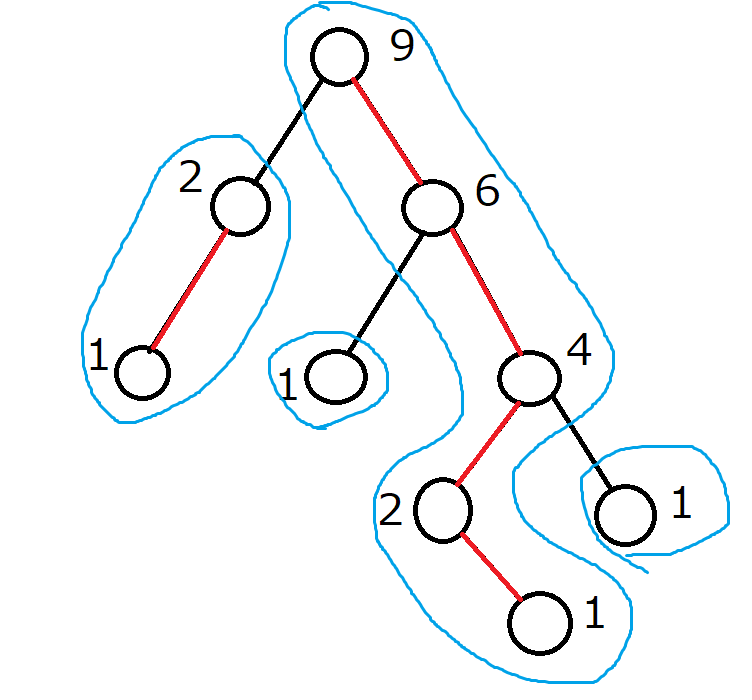
実はこれでHL分解は完了です。
図を整理してわかりやすくすると次のようになります。
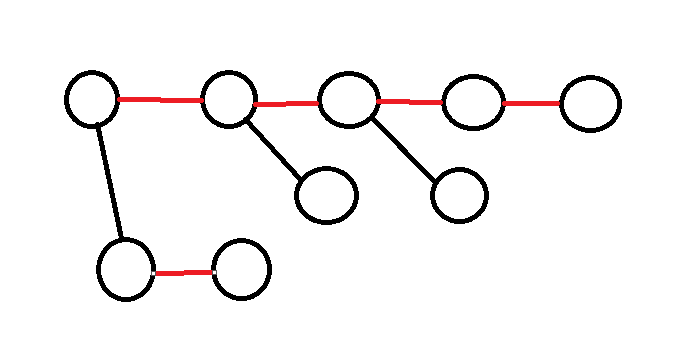
これで、深さが高々 $O(\log N)$ の、ノードが列を表す木に分解できました。
これは、Heavyでない辺でつながれた先のノードのかたまりのサイズは、親のサイズの半分以下であることから示せます。
こうすれば、先ほどの頂点間距離のクエリも、それぞれの列について $O(\log N)$,見るべき列も $O(\log N)$ 個なので、結局 $O(\log^2 N)$ で求まりますね。
もちろん、全体の計算量は列に対する計算量に依存するので、列に対する操作が $O(1)$ のものなら全体では $O(\log N)$ になります。
実用例
ここで、典型的なHLDが使える問題のひとつである、高速道路を例に挙げて説明します。
この問題では、2頂点間の距離を、方向によって辺の長さが異なる木上で求めなければいけません。
また、辺の長さを変更するクエリも与えられます。
ここでHLDを使うと、パスについて、2種類の向きにBITなどのデータ構造を持っておき、2頂点間の距離クエリに対しては、木を愚直にさかのぼっていくことで答えられます。
HLDの後の木の深さは最大 $O(\log N)$ なのも考えると、これで十分高速です。
こうして、HLDを利用すると木に対する変更のクエリが高速に処理できるのです。
実装
かなり重いです。
上の問題の提出リンク
もっと軽い実装もあるみたいですが、最初のうちは注意深く素直に実装したほうがバグらせにくいだろうとは感じました。
おわりに
これで、3大頭が良いけど頻繁には使わなさそう(要出典)アルゴリズム(CHT,FFT,HLD)の記事を制覇しました。
木に対するある意味実家なアルゴリズムなので、覚えておきましょう。