Python 少ない点に対する近似曲線 スプライン曲線との比較

比較

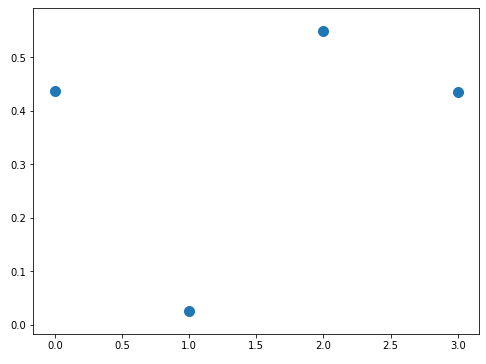
ランダム点の散布図です。これらのランダム点に対して近似曲線とスプライン曲線を引いてみます。ただし、近似曲線は、少ない点に対する近似曲線で紹介した中間ランダム点を使って引きます。

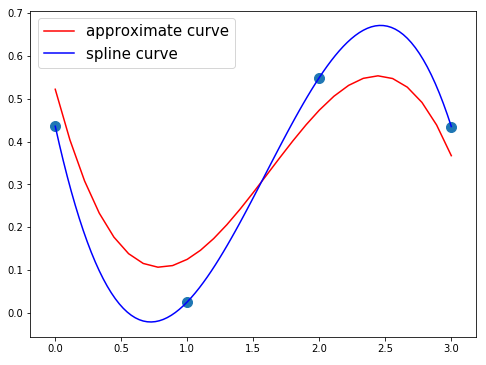
• ランダム点4個、近似曲線の次数3

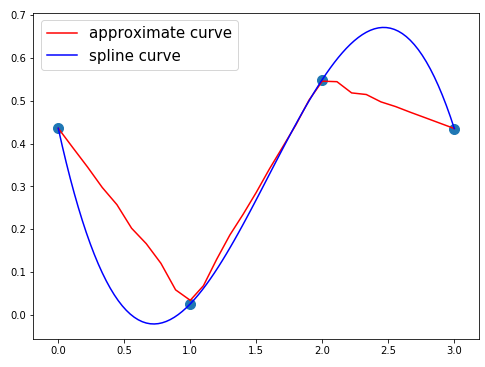
• ランダム点4個、近似曲線の次数30

近似曲線の次数を大きくすればランダム点の極値（のように見える点）の付近で極値を取ってくれます。

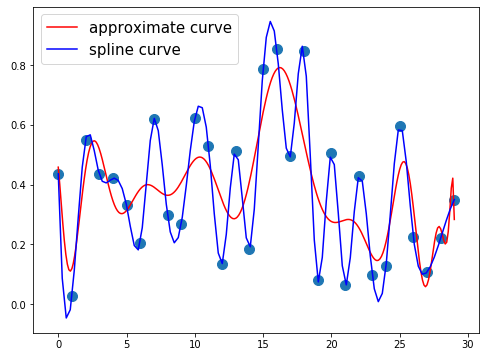
• ランダム点30個、近似曲線の次数30

ランダム点を増やすとスプライン曲線の方が良い挙動をしています。
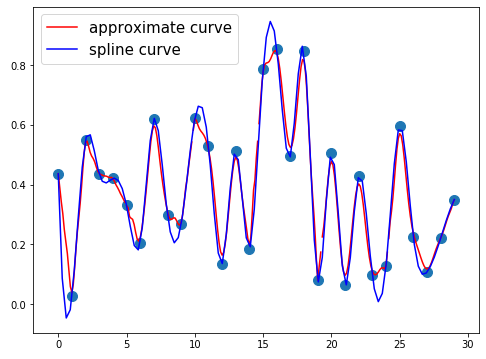
最後に少ない点に対する近似曲線2で紹介した近似曲線を分割する方法で比較してみます。

• ランダム点30個、近似曲線の次数60、中間ランダム点の分割数6

所感

• スプライン曲線

  • メリット
    • 連続性
  • デメリット
    • 極大ランダム点または極小ランダム点において大きなずれが見て取れる

• 分割近似曲線

  • メリット
    • 極大ランダム点と極小ランダム点におけるずれが少ない
  • デメリット
    • 不連続

ランダム点の個数や間隔、次数など曲線に影響を与える要素が多く、簡単には比較できないです。ですので上記の考察は非常に特別な場合に限ったものであり、一般には詳細な検証が必要だと思われます。

検証に使用したコード

sample8.py

from scipy import interpolate
import matplotlib.pyplot as plt
import numpy as np
import random
import math

SIZE = 30
SEED = 2
DEGREE = 60
SPLIT_DISTANCE = 0.1 # 2点のランダム点の距離を0.1の長さに分割する
SPLIT_ARRAY = 6 # 中間ランダム点の分割数
LINSPACE_SIZE = 100 # スプライン曲線を引くための区間の分割サイズ
plt.figure(figsize=(8.0, 6.0))

def plot_split(x_val1, x_val2, y_val1, y_val2, x_medium_points, y_medium_points):
    """
    各ランダム点の中間点を生成するメソッド
    (x_val1, y_val1), (x_val2, y_val2): 2点のランダム点
    x_medium_points: 中間点のx座標をすべて格納する配列
    y_medium_points: 中間点のy座標をすべて格納する配列
    """
    # 2点のランダム点の距離を計算
    distance = math.sqrt(math.pow(x_val2 - x_val1, 2) + math.pow(y_val2 - y_val1, 2))
    # 必要な中間点の数を計算
    spl_num = math.floor(distance / SPLIT_DISTANCE)
    # 2点のランダム点を分割する. (x, y)が中間点の座標
    x_ = np.linspace(x_val1 ,x_val2, spl_num)
    y_ = np.linspace(y_val1 ,y_val2, spl_num)
    # 中間点を追加する
    x_medium_points = np.append(x_medium_points, x_)
    y_medium_points = np.append(y_medium_points, y_)
    return x_medium_points, y_medium_points


def plot_split_curve(x_medium_points, y_medium_points, DEGREE, n=0):
    """
    分割した近似曲線を描画するメソッド
    """
    coeff = np.polyfit(x_medium_points, y_medium_points, DEGREE)
    y_polyfit = np.poly1d(coeff)(x_medium_points)
    # このコメントアウトはグラフを見やすくするため
    # コメントアウトを外すと中間ランダム点が描画される
    # plt.scatter(x_medium_points, y_medium_points, marker='o')
    if n == 0:
        plt.plot(x_medium_points, y_polyfit, label='approximate curve', color='red')
    else:
        plt.plot(x_medium_points, y_polyfit, color='red')  

def plot_spline_curve(x, y):
    """
    スプライン曲線を描画するメソッド
    """
    f = interpolate.interp1d(x, y, kind="cubic")
    x_linspace_points = np.linspace(0, len(x) - 1, num=LINSPACE_SIZE)
    y_linspace_points = f(x_linspace_points)
    plt.plot(x_linspace_points, y_linspace_points, color='blue', label="spline curve")
    
def plot_curve():
    """
    近似曲線を描画するメソッド
    """
    np.random.seed(seed=SEED)

    x = np.array(range(SIZE))
    y = np.random.rand(SIZE)
    x_medium_points = np.empty(0) # すべての中間点のx座標を格納するndarray
    y_medium_points = np.empty(0) # すべての中間点のy座標を格納するndarray
    # すべてのランダム点間を分割するループ
    for i in range(SIZE - 1):
        x_medium_points, y_medium_points = plot_split(
            x[i], x[i + 1], y[i], y[i + 1], x_medium_points, y_medium_points
        )
    # ndarrayの分割
    for n, x_split_array, y_split_array in zip(
        range(SPLIT_ARRAY),
        np.array_split(x_medium_points, SPLIT_ARRAY),
        np.array_split(y_medium_points, SPLIT_ARRAY)
    ):
        # 近似曲線を描画
        plot_split_curve(x_split_array, y_split_array, DEGREE, n)
    # スプライン曲線を描画
    plot_spline_curve(x, y)
    # ランダム点を描画
    plt.scatter(x, y, marker='o', s=100)
    plt.tick_params(labelsize=10)
    plt.rc('legend', fontsize=15)
    plt.legend()
    plt.show()

plot_curve()

参考記事