グラフとBFS(幅優先探索)・DFS(深さ優先探索)をJSで実装してみる

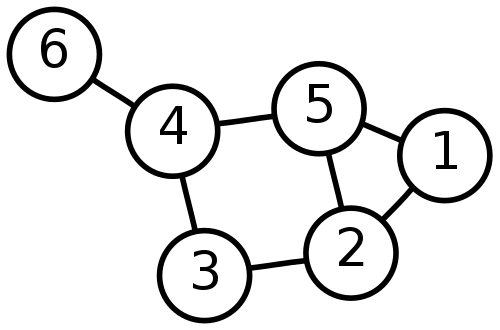
この記事で言うグラフは、折れ線グラフなどのグラフでは無く「データ構造」のグラフです。
ノード（頂点）群とノード間の連結関係を表すエッジ（枝）群で構成されるデータ型です。

実際のコード

class Graph {
    constructor() {
        this.connectedList = {};
    }
    
    addVertex(vertex) {
        this.connectedList[vertex] = []
    }
    
    addEdge(v1, v2) {
        this.connectedList[v1].push(v2);
        this.connectedList[v2].push(v1);
    }
    
    removeEdge(vertex1, vertex2) {
        this.connectedList[vertex1] = this.connectedList[vertex1].filter(
            v => v !== vertex2
        );
        
        this.connectedList[vertex2] = this.connectedList[vertex2].filter(
            v => v !== vertex1
        );
    }
    
    removeVertex(vertex) {
        while (this.adjacencyList[vertex].length) {
            const adjacentVertex = this.adjacencyList[vertex].pop();
            this.removeEdge(vertex, adjacentVertex);
        }
        
        delete this.adjacencyList[vertex];
    }

    dfs(start) {
      //ノードを格納するスタック
      const stack = [start];

      //訪れた順番を格納
      const result = [];

      //訪れたフラグ
      const visited = {};

      //現在のノード
      let currentVertex;

      //訪問済みフラグを立てる
      visited[start] = true;

      while (stack.length) {
        // stackの最後尾を取得&削除
        currentVertex = stack.pop();

        // resultに現在の頂点を追加
        result.push(currentVertex);

        // 繋がっている頂点を探索して訪問済みにする
        // そして、stackにその頂点を追加
        this.connectedList[currentVertex].forEach(neighbor => {
          if (!visited[neighbor]) {
            visited[neighbor] = true;
            stack.push(neighbor);
          }
        });
      }
      return result;
    }

    bfs(start) {
      // これから探索する予定のものの配列
      const queue = [start];

      // 訪問順番の結果
      const result = [];

      // 探索済みであるか
      const visited = {};

      let currentVertex;
      visited[start] = true;

      while (queue.length) {
        // 先頭から取り出す
        currentVertex = queue.shift();

        // 現在地点を探索済みに
        result.push(currentVertex);

        this.connectedList[currentVertex].forEach(neighbor => {
          if (!visited[neighbor]) {
            visited[neighbor] = true;
            queue.push(neighbor);
          }
        });
      }
      return result;
    }
}

const graph = new Graph;

// 頂点の追加
graph.addVertex(1)
graph.addVertex(2)
graph.addVertex(3)
graph.addVertex(4)
graph.addVertex(5)
graph.addVertex(6)
graph.addVertex(7)

// エッジ(繋がり)の追加
graph.addEdge(1, 2)
graph.addEdge(1, 3)
graph.addEdge(2, 4)
graph.addEdge(4, 6)
graph.addEdge(3, 6)
graph.addEdge(4, 6)
graph.addEdge(4, 5)
graph.addEdge(5, 7)

// 幅探索を行う
console.log(graph.dfs(1)) // 1, 3, 6, 4, 5, 7, 2

// 深さ探索を行う
console.log(graph.bfs(1)) // 1, 2, 3, 4, 6, 5, 7

使いどころ

町1から町2に道が繋がっていてお互いを行き来出来るなどといった関係性を表すのに使うやつです。
Twitterのフォローフォロワーとかもグラフみたいなものなので意外と色々なところで使われます。