交代級数(Alternating Series)概念は数列の次元では符号問題から出発し(1次元上において0度と180度の中間段階としての±90度を扱う為の)虚数(Imaginal)$i^2=-1$概念へと到達します。
【数理考古学】解析学史に「虚数概念」をもたらした交代級数
一方、関数の次元においてそれは(y=f(x)のグラフがy軸対称となり、f(-x)=f(x)の形で定義される)偶関数(Even Function)と(y=f(x)$f_e(x)$のグラフが原点対称となり、f(-x)=-f(x)の形で定義される)奇関数(Odd Function)$f_o(x)$の関係として立ち現れてくるのです(①②)。
偶関数・奇関数とは?意味や見分け方、積分での使い方
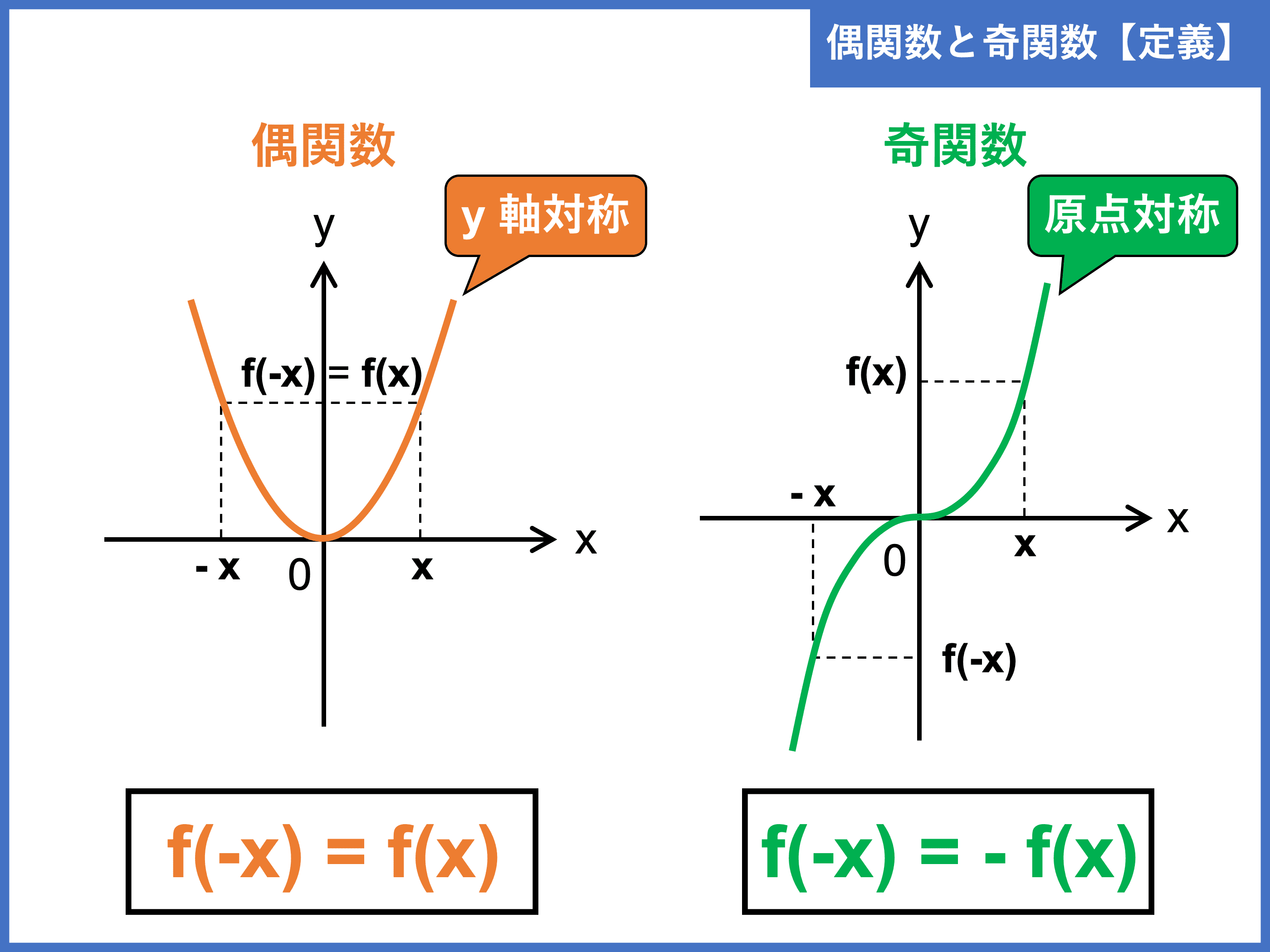
f_e(x)=\frac{f(x)+f(-x)}{2},f_o(x)=\frac{f(x)-f(-x)}{2}\\
なぜならば\\
f_e(-x)=\frac{f(-x)+f(-(-x))}{2}=\frac{f(-x)+f(x)}{2}=f_e(x)…①\\
f_o(-x)=\frac{f(-x)-f(-(-x))}{2}=\frac{f(-x)-f(x)}{2}=-\frac{f(-x)+f(-x))}{2}=-f_o(x)…②
任意の関数は偶関数と奇関数の和(一時結合的表現)によって表せる。
関数空間V上の任意の関数f(x)($\forall f(x) \in \mathbb{V}$)は偶関数$f_e(x)$と奇関数$f_o(x)$の和として表せる(③=一次接合的表現)。その差は-f(x)となるが、その結果がどうなるかはその任意の関数が奇関数か偶関数かどちらでもないかによる(④)。
f_e(x)+f_o(x)=\frac{f(x)+f(-x)}{2}+\frac{f(x)-f(-x)}{2}=f(x)…③\\
f_e(x)-f_o(x)=\frac{f(x)+f(-x)}{2}-\frac{f(x)-f(-x)}{2}=-f(x)…④
偶関数と奇関数の加減乗除
偶関数と偶関数の和と差と積は偶関数となる(⑤⑦)。奇関数と奇関数の和と差と積は奇関数となる(⑥⑧)。偶関数と奇関数の積は奇関数となる(⑨)。
f_e(x)±g_e(x)=h(x)の時\\
h(-x)=f_e(-x)±g_e(-x)=f_e(x)±g_e(x)=h(x)…⑤\\
f_o(x)±g_o(x)=h(x)の時\\
h(-x)=f_o(-x)±g_o(-x)=-f_o(x) \mp g_o(x)\\
=-(f_o(x)±g_o(x))=h(-x)…⑥\\
f_e(x)g_e(x)=h(x)の時\\
h(-x)=f_e(-x)g_e(-x)=f_e(x)g_e(x)=h(x)…⑦\\
f_e(x)g_e(x)=h(x)の時\\
h(-x)=f_o(-x)g_o(-x)=(-f_o(x))(-g_o(x))\\
=-(f_o(x)g_o(x))=h(-x)…⑧\\
f_e(x)g_o(x)=h(x)の時\\
h(-x)=f_e(-x)g_o(-x)=(f_e(x))(-g_o(x))=h(-x)…⑨\\
偶関数と奇関数の積分結果
任意の実数aによって積分範囲-a≥x≧a($\forall a \in \mathbb{R}$)が規定される偶関数$f_e(x)$と奇関数$f_o(x)$について以下が成立する。
偶関数・奇関数とは?意味や見分け方、積分での使い方
\int_{−a}^a f_e(x)dx = 2 \int_0^a f_e(x)dx\\
\int_{−a}^a f_o(x)dx = 0
実例その1:自然指数関数(Natural Exponential Function)の場合
自然指数関数(Natural Exponential Function)$y=e^x=/cosh x + \sinh x$の場合は以下となります。
双曲線関数にまつわる重要な公式まとめ
cosh(x),sinh(x),tanh(x)

e^x=\cosh x + \sinh x\\
\cosh x = \frac{e^x+e^{-x}}{2}\\
\sinh x = \frac{e^x-e^{-x}}{2}\\
\tanh x = \frac{\sinh x}{\cosh x}=\frac{e^x-e^{-x}}{e^x+e^{-x}}
実例その2:オイラーの公式(Eulerian Formula)の場合
オイラーの公式(Eulerian Formula)$y=e^{xi}=\cos x + \sin xi$の場合は以下となります。
【Python演算処理】等速円運動についての物理学と数学の立場の違い?
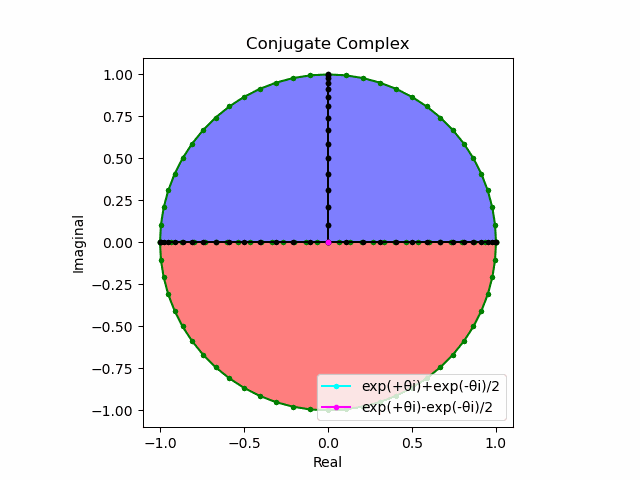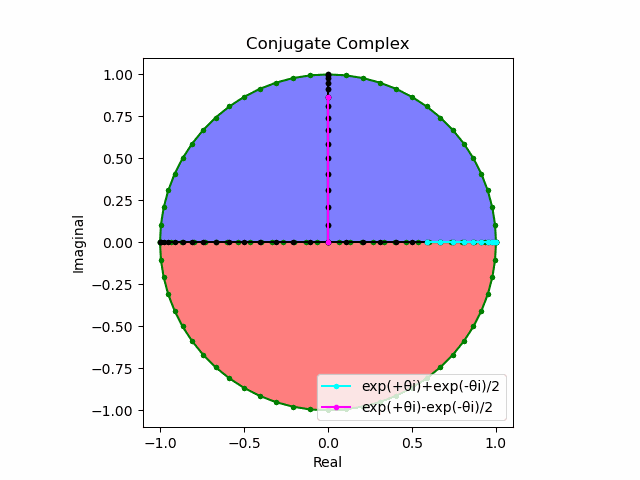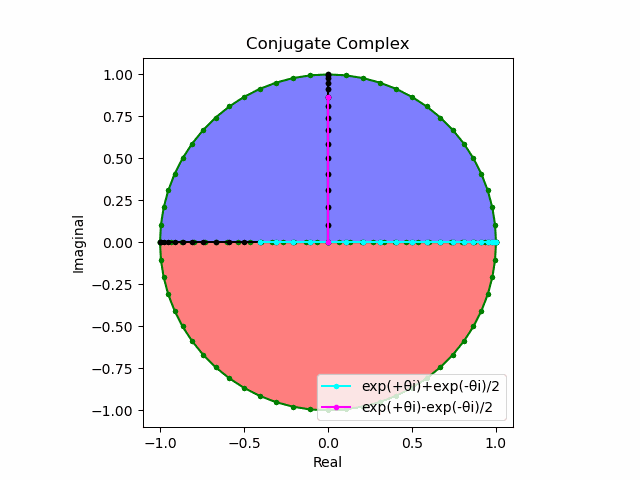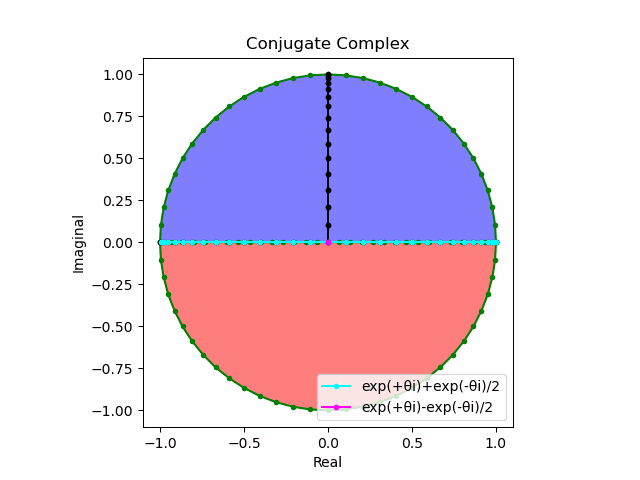
e^{xi}=\cosh x + \sinh xi\\
\cos x = \frac{e^{xi}+e^{-xi}}{2}\\
\sin x = \frac{e^{xi}-e^{-xi}}{2}\\
\ tan x = \frac{\sin x}{\cos x}=\frac{e^{xi}-e^{-xi}}{e^{xi}+e^{-xi}}
そう、この二つの関数の違いは「1次元空間の局所に極座標的演算を付加する」虚数概念(Imaginal)$i^2=-1$の導入有無だけなのです。そんな感じで以下続報…