モデルの視覚的な確認
予測値の視覚化
一般化線形モデルや一般化線形混合モデルによる解析をRで行う際、よく用いられるのはglmやglmerです。これらの関数による解析結果は数値的なアウトプットとして得られます。しかし、数値のみからモデルを直感的に解釈することは難しいです。
その際に役立つのがモデルで記述される説明変数と応答変数の関係を予測値や回帰線のプロットによって表現したグラフです。グラフを見ることでモデルを直感的に解釈することが可能になります。
回帰線を描く難しさ
一方で、glmやglmerの結果からこれらのグラフのプロットを行うのは結構面倒です。これはオブジェクトからのデータ抽出や説明変数の条件設定、出力結果の整形に煩雑なコードが必要となるからです。特に、ggplot2の描画システムに合わせた描画用データを作成するのには手間がかかります。
またggplot2::geom_smoothが回帰線を描く関数としてよく挙げられますが、この関数ではすでに実行したglmやglmerの結果から回帰線を描画することが出来ません(glmに関しては工夫すれば出来ないことはないようですが(参考))。そして2次元データを可視化することに特化したggplot2の特性上、基本的には説明変数が一つのモデルしか使うことができません。
ggeffectsパッケージで解決できる!
この問題の解決に役立つのがggeffectsパッケージです。ggeffectsはモデルに基づく周辺平均(marginal mean)の推定値を簡単に計算するこができるパッケージです。
ggeffectsパッケージとggplot2を組み合わせて使うことで、glmやglmerの結果から目的に合った予測値や回帰線のプロットを簡単に行うことができます。ここではその一例を紹介したいと思います。
例により、詳しい統計学的な説明の方はしない(できない)ので使い方のメモとして見てください。レポートなどに用いる際にはパッケージのヘルプやレファレンス、ソースコード等を見て導出過程や計算方法を確認するのが良いと思います。
ggeffectsは複数のクラスのオブジェクトに対応しており、かなり柔軟な使い方ができるので、ぜひ一度公式レファレンスを見てみてください。
この記事は「こんな使い方ができるよ」的な例として見れもらえればと思います。
また信頼区間の算出方法については注意点があるので後述の説明も参考にしてください。
インストール
CRANとGitHubどちらからでもインストールできます。GitHubは更新が速いので安定版を使いたいのであればCRANのほうがおすすめです。
- CRAN
install.packages("ggeffects")
- GitHub
remotes::install_github("strengejacke/ggeffects")
ggeffects::ggpredictについて
今回は回帰線を描画するための予測値および信頼区間の取得にggeffects::ggpredictを使用します。
ggpredictは総称的関数であるpredictを使用して予測値を取得します。ヘルプの内容を受けて考えるなら、glmの結果に対して適用した際にはpredict.glmが、glmerの結果に対して適用した際にはpredict.merModで予測値が算出されていると見て良いでしょう。
ggeffestsには予測値を取得するための関数として他にもggeffectとggemmeansがあり、これらはそれぞれeffects::Effect、emmeans::emmeansを予測値の取得に使用しています。
注意:信頼区間について
ggeffectsの良いところとして信頼区間の描画も簡単にできることが挙げられますが、glmやglmerの予測値に対する信頼区間は理解や解釈が難しいものであると思います。使用の際にはその点にご注意ください。
信頼区間は予測値のSEに基づき「± 1.959964... x SE」で算出されます。
SEは、predictで算出される場合はその値が用いられます。predict.merModのようなSEを算出しない関数が使用される場合には、パラメータの分散共分散行列に基づいて計算されるようです。
後述するランダム効果を考慮した場合の信頼区間は、ランダム効果を考慮した分散共分散行列に基づいて算出されるようです。
詳しくはこちらのページの「Short technical note」とこちらのページのtype = "re"についての説明を確認してください。
ここらへんの導出過程の詳しい解説は出来ないです。すみません。(GLMやGLMMの仕組みそのものに深く関わるので難しいです)
統計学的な背景が理解できていないのであれば、下手に自分で計算しようとせずに専門家が作成したこのようなパッケージを使用するのも、個人的にはありだと思います。一方で、計算の中身がわからない状態が気持ち悪いならば、理解した上で自分で予測値やSE等の計算を行うのが良いと思います。
ここらへんは用途や統計手法の使い方に対する態度によりけりです。
どちらにせよ、前述のとおり、レポート等に使用する際にはレファレンスやソースコードを確認することをおすすめします。
回帰線の描画
ggeffects::plotを使った描画例とggplot2での描画例を示します。
ggeffects::plotはggeffects::ggpredictによる予測値を簡単にプロットできる関数です。ggeffects::plotを使ってもかなりきれいに柔軟に図を作れるので、こちらのレファレンスから使い方を確認していただければと思います。
glmの方でggpredictの基本的にな使い方を解説して、glmerの方でランダム効果がある場合の描画例について解説します。
ggpredictの詳しい使い方はこちらのリファレンスで確認できるので、そちらも参照しながら以下の例を見ていただければと思います。
使用するパッケージ
ここでは以下のパッケージを使用します。
library(ggeffects)
library(tidyverse)
library(lme4)
library(MASS)
glm
基本的な使い方
基本的には、glm等を実行 → ggpredictを適用 → 予測値に基づいて描画の流れです。
簡単に言えば、termsにx軸にしたい説明変数を与えてしまえば、その説明変数の範囲内における予測値と信頼区間が出てきます。
- x軸に連続値を指定する場合
まず説明変数が1つの例で基本的な使い方を解説します。glmを実行し、その結果に対しggpredictを適用し、予測値を取得します。
> glm0a <- glm(vs ~ wt, data = mtcars, family = "binomial")
>
> (glm0a_p <- ggpredict(glm0a, terms = "wt"))
Data were 'prettified'. Consider using `terms="wt [all]"` to get smooth plots.
# Predicted values of vs
# x = wt
x | Predicted | SE | 95% CI
--------------------------------------
1.40 | 0.95 | 1.32 | [0.61, 1.00]
2.00 | 0.87 | 0.92 | [0.52, 0.98]
2.40 | 0.76 | 0.67 | [0.45, 0.92]
2.80 | 0.59 | 0.49 | [0.35, 0.79]
3.40 | 0.31 | 0.49 | [0.15, 0.54]
4.00 | 0.13 | 0.79 | [0.03, 0.40]
4.40 | 0.06 | 1.04 | [0.01, 0.34]
5.40 | 0.01 | 1.73 | [0.00, 0.23]
ggpredictのコンソール出力は上のようになっていますが中身は以下のようなデータフレームです:
> glm0a_p %>% as_tibble()
# A tibble: 21 x 6
x predicted std.error conf.low conf.high group
<dbl> <dbl> <dbl> <dbl> <dbl> <fct>
1 1.4 0.954 1.32 0.613 0.996 1
2 1.6 0.934 1.18 0.586 0.993 1
3 1.8 0.907 1.05 0.556 0.987 1
4 2 0.869 0.915 0.525 0.976 1
5 2.2 0.819 0.791 0.491 0.955 1
6 2.4 0.756 0.674 0.452 0.921 1
7 2.6 0.679 0.572 0.408 0.866 1
8 2.8 0.590 0.491 0.355 0.790 1
9 3 0.496 0.445 0.291 0.702 1
10 3.2 0.402 0.444 0.219 0.616 1
# … with 11 more rows
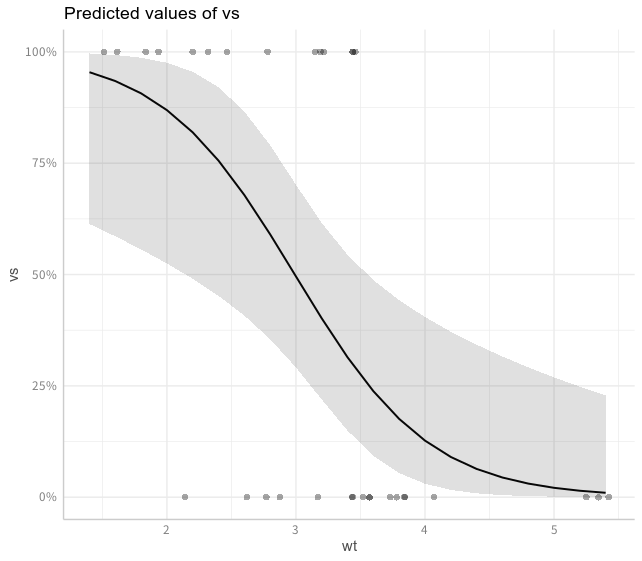
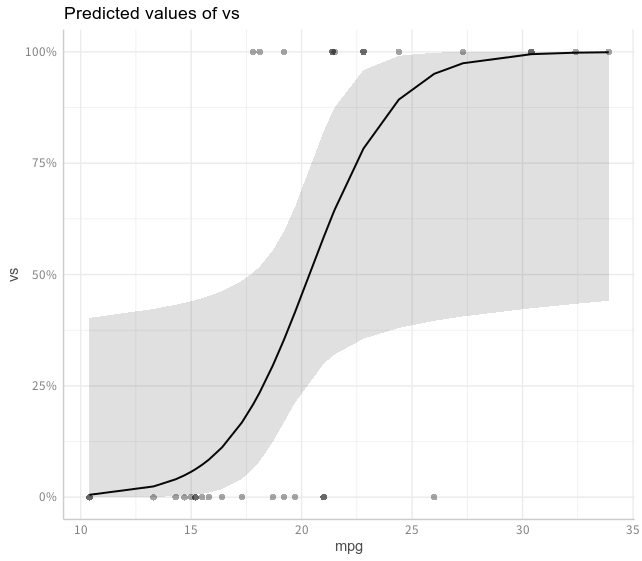
まずggeffects::plotを使うことで簡単に回帰線を表示できます。また、rawdata = Tを指定することで元データも同時に表示できます。
> plot(glm0a_p, rawdata = T)
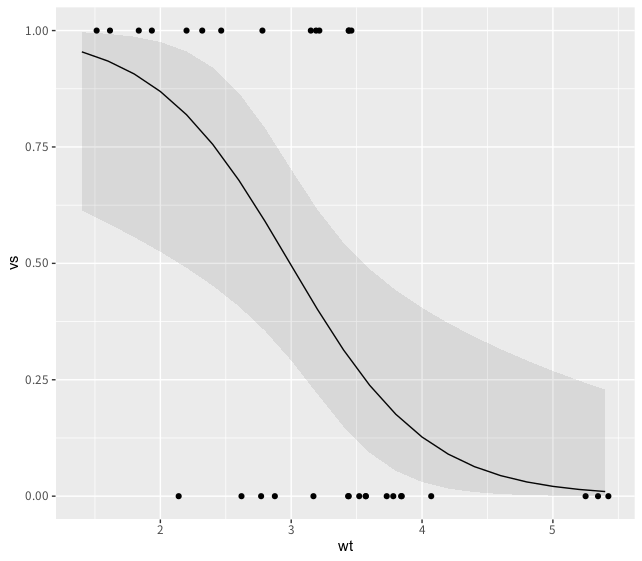
ggplot2でも描画してみましょう。データの構造を活かせば数行で回帰線を描画できます。
> ggplot() +
+ geom_point(data = mtcars, aes(x = wt, y = vs)) +
+ geom_line(data = glm0a_p, aes(x = x, y = predicted)) +
+ geom_ribbon(data = glm0a_p, aes(x = x, ymin = conf.low, ymax = conf.high), alpha = 0.1)
- x軸に因子を指定する場合
x軸に連続値ではなく因子を指定する場合も同様にtermsに説明変数を指定します。
ただしこの場合には回帰線とはならず、因子ごとの予測値がプロットされます。
> mtcars2 <- mtcars
> mtcars2$gear <- as.factor(mtcars2$gear)
> glm0b <- glm(mpg ~ gear, family = "gaussian", data = mtcars2)
>
> (glm0b_p <- ggpredict(glm0b, terms = "gear"))
# Predicted values of mpg
# x = gear
x | Predicted | SE | 95% CI
-------------------------------------
3 | 16.11 | 1.22 | [13.72, 18.49]
4 | 24.53 | 1.36 | [21.87, 27.20]
5 | 21.38 | 2.11 | [17.25, 25.51]
>
> glm0b_p %>% as_tibble()
# A tibble: 3 x 6
x predicted std.error conf.low conf.high group
<fct> <dbl> <dbl> <dbl> <dbl> <fct>
1 3 16.1 1.22 13.7 18.5 1
2 4 24.5 1.36 21.9 27.2 1
3 5 21.4 2.11 17.3 25.5 1
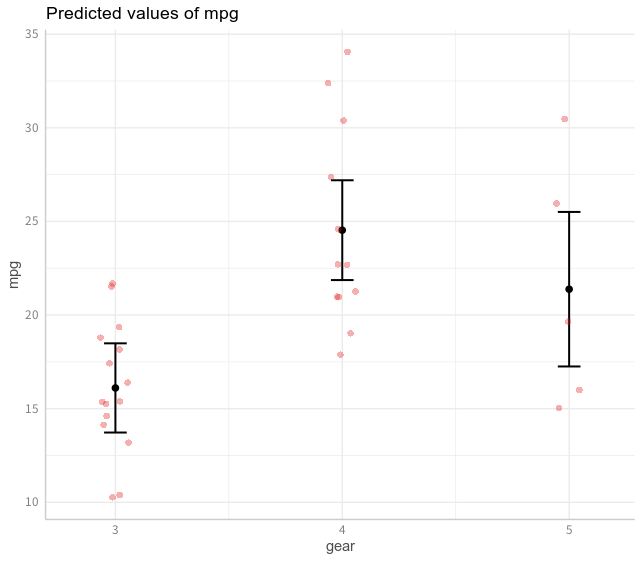
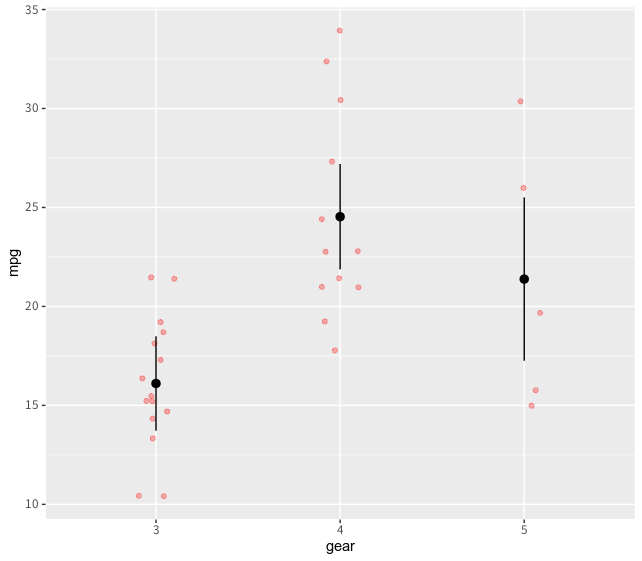
plotで描画すると以下のようになります。geom_pointrangeを使うといい感じにプロットできます。
> plot(glm0b_p, rawdata = T)
ggplot2で描画すると以下のようになります。
> ggplot() +
+ geom_point(data = mtcars2, aes(x = gear, y = mpg), col = "red", alpha = 0.3, position = position_jitter(width = 0.1)) +
+ geom_pointrange(data = glm0b_p, aes(x = x, y = predicted, ymin = conf.low, ymax = conf.high))
termsとconditionの指定
termsに指定する変数が1つの場合
説明変数が1つの場合には上述のようになります。
一方で、ggeffectsが真価を発揮するのは説明変数が複数ある場合です。
まず、説明変数が2つの場合の例について見てみようと思います.
> glm1 <- glm(vs ~ wt + mpg, family = "binomial", data = mtcars)
>
> (glm1_p1 <- ggpredict(glm1, terms = "mpg [all]", condition = c(wt = mean(mtcars$wt))))
# Predicted values of vs
# x = mpg
x | Predicted | SE | 95% CI
---------------------------------------
10.40 | 0.01 | 2.46 | [0.00, 0.40]
14.70 | 0.05 | 1.38 | [0.00, 0.44]
15.50 | 0.07 | 1.19 | [0.01, 0.45]
17.30 | 0.17 | 0.79 | [0.04, 0.49]
18.70 | 0.30 | 0.55 | [0.12, 0.55]
21.00 | 0.58 | 0.61 | [0.30, 0.82]
22.80 | 0.78 | 0.96 | [0.36, 0.96]
33.90 | 1.00 | 3.74 | [0.44, 1.00]
>
> glm1_p1 %>% as_tibble()
# A tibble: 25 x 6
x predicted std.error conf.low conf.high group
<dbl> <dbl> <dbl> <dbl> <dbl> <fct>
1 10.4 0.00540 2.46 0.0000438 0.403 1
2 13.3 0.0242 1.73 0.000841 0.423 1
3 14.3 0.0402 1.48 0.00230 0.432 1
4 14.7 0.0492 1.38 0.00344 0.437 1
5 15 0.0571 1.31 0.00463 0.440 1
6 15.2 0.0630 1.26 0.00565 0.443 1
7 15.5 0.0729 1.19 0.00759 0.447 1
8 15.8 0.0843 1.12 0.0102 0.452 1
9 16.4 0.112 0.981 0.0181 0.463 1
10 17.3 0.168 0.787 0.0414 0.486 1
# … with 15 more rows
termsが基本的に説明変数を指定する部分なのですが、ここに指定するのはx軸にしたい値です。termsには説明変数名を指定できますが、半角スペース+[]でオプションを指定することも出来ます。上記の例ではmpg [all]で元データのmpgの値の範囲全域における予測値を出すように指定しています。
x軸に使用しない説明変数の値はconditionで指定できます。ここではwtの値をwtの平均値に固定しています。
つまりこれらをうまく指定することで、実際には多次元平面(曲面?)上に存在する予測値を二次元平面上の回帰線として描画することが可能になります。
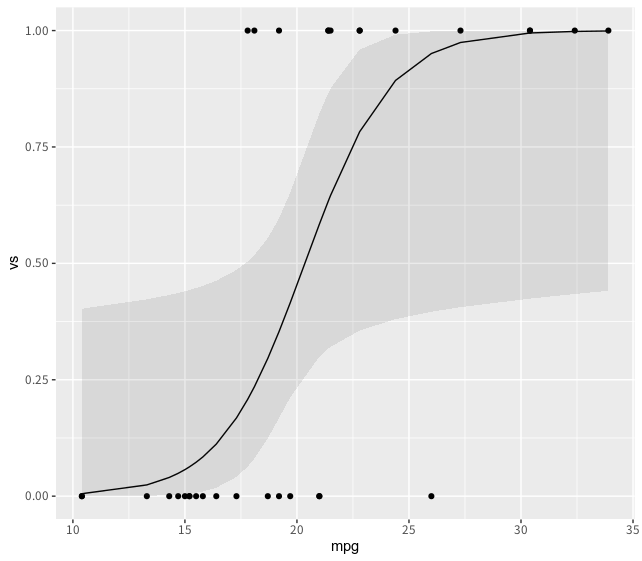
まず簡単にプロットするとこんな感じです。
> plot(glm1_p1, rawdata = T)
ggplot2で描画するとこんな感じになります。
> ggplot() +
+ geom_point(data = mtcars, aes(x = mpg, y = vs)) +
+ geom_line(data = glm1_p1, aes(x = x, y = predicted)) +
+ geom_ribbon(data = glm1_p1, aes(x = x, ymin = conf.low, ymax = conf.high), alpha = 0.1)
termsに指定する変数が2つの場合
上記の例ではtermsに説明変数を指定しました。実はtermsには3つまで説明変数を指定できます。まずは2つの場合。
> (glm1_p2 <- ggpredict(glm1, terms = c("mpg [all]", "wt [meansd]")))
# Predicted values of vs
# x = mpg
# wt = 2.24
x | Predicted | SE | 95% CI
---------------------------------------
10.40 | 0.00 | 3.43 | [0.00, 0.72]
15.00 | 0.03 | 2.29 | [0.00, 0.75]
16.40 | 0.07 | 1.96 | [0.00, 0.77]
18.70 | 0.19 | 1.45 | [0.01, 0.80]
21.40 | 0.49 | 0.98 | [0.13, 0.87]
33.90 | 1.00 | 2.93 | [0.69, 1.00]
# wt = 3.22
x | Predicted | SE | 95% CI
---------------------------------------
10.40 | 0.01 | 2.46 | [0.00, 0.40]
15.00 | 0.06 | 1.31 | [0.00, 0.44]
16.40 | 0.11 | 0.98 | [0.02, 0.46]
18.70 | 0.30 | 0.55 | [0.12, 0.55]
21.40 | 0.63 | 0.67 | [0.32, 0.87]
33.90 | 1.00 | 3.75 | [0.44, 1.00]
# wt = 4.2
x | Predicted | SE | 95% CI
---------------------------------------
10.40 | 0.01 | 1.73 | [0.00, 0.22]
15.00 | 0.10 | 0.92 | [0.02, 0.39]
16.40 | 0.18 | 0.87 | [0.04, 0.55]
18.70 | 0.43 | 1.10 | [0.08, 0.87]
21.40 | 0.75 | 1.63 | [0.11, 0.99]
33.90 | 1.00 | 4.71 | [0.17, 1.00]
>
> glm1_p2 %>% as_tibble()
# A tibble: 75 x 6
x predicted std.error conf.low conf.high group
<dbl> <dbl> <dbl> <dbl> <dbl> <fct>
1 10.4 0.00306 3.43 0.00000368 0.720 2.24
2 10.4 0.00541 2.46 0.0000440 0.402 3.22
3 10.4 0.00954 1.73 0.000325 0.222 4.2
4 13.3 0.0138 2.71 0.0000695 0.739 2.24
5 13.3 0.0243 1.72 0.000846 0.422 3.22
6 13.3 0.0422 1.14 0.00467 0.292 4.2
7 14.3 0.0232 2.46 0.000190 0.748 2.24
8 14.3 0.0403 1.48 0.00232 0.431 3.22
9 14.3 0.0692 0.994 0.0105 0.343 4.2
10 14.7 0.0284 2.37 0.000283 0.751 2.24
# … with 65 more rows
termsで1番目に指定した説明変数はx軸になりますが、2番目に指定した説明変数はグループとして扱われます。つまり、グループごとの予測値が算出された上でデータフレームに出力されます。コンソール出力ではグループごとの予測値が表示されます。
2番目に指定した説明変数が因子型だった場合には因子がグループ分けにそのまま用いられます。連続値だった場合には「平均値-標準偏差」、「平均値」、「平均値+標準偏差」の3グループが用いられるようです。ここの例では"wt [meansd]"でグループを明示的に指定しています。
このグループの値はaesのcolorに指定することで回帰線を重ね書きできるようになります。
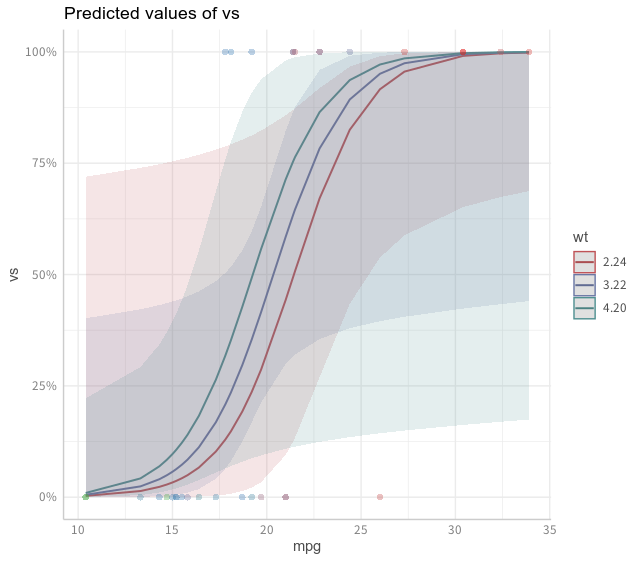
plotで確認すると以下のようになります。
plot(glm1_p2, rawdata = T)
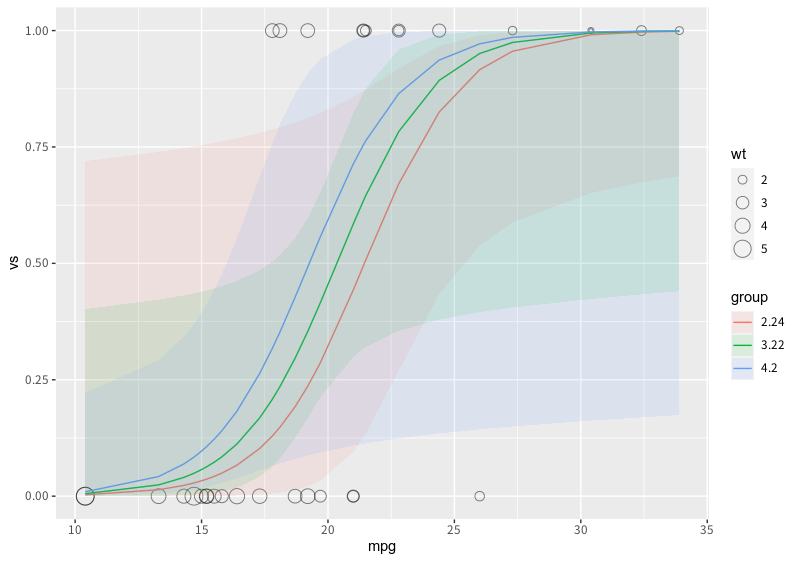
ggplot2で描画すると例えば以下のように出来ます。sizeでwtの値を視覚化しています。
> ggplot() +
+ geom_point(data = mtcars, aes(x = mpg, y = vs, size = wt), shape = 1, alpha = 0.5) +
+ geom_line(data = glm1_p2, aes(x = x, y = predicted, color = group)) +
+ geom_ribbon(data = glm1_p2, aes(x = x, ymin = conf.low, ymax = conf.high, fill = group), alpha = 0.1)
termsに指定する変数が3つの場合
最後はtermsに指定する説明変数が3つある場合です。ここでは説明変数が4つある場合を例に示してみます。
> epil0 <- epil
> epil0$V4 <- as.factor(epil0$V4)
> epil0$subject <- as.factor(epil0$subject)
>
> glm2 <- glm(y ~ lbase*trt + lage + V4, family = "poisson", data = epil0)
>
> (glm2_p <- ggpredict(glm2, terms = c("lbase", "trt", "V4"), condition = c(lage = mean(epil0$lage))))
# Predicted values of y
# x = lbase
# trt = placebo
# V4 = 0
x | Predicted | SE | 95% CI
-----------------------------------------
-1.40 | 1.77 | 0.09 | [ 1.48, 2.12]
-0.80 | 3.12 | 0.07 | [ 2.73, 3.57]
-0.20 | 5.52 | 0.05 | [ 5.02, 6.06]
0.60 | 11.79 | 0.04 | [11.00, 12.64]
1.80 | 36.80 | 0.07 | [32.39, 41.81]
# trt = progabide
# V4 = 0
x | Predicted | SE | 95% CI
-----------------------------------------
-1.40 | 0.57 | 0.10 | [ 0.47, 0.70]
-0.80 | 1.41 | 0.08 | [ 1.21, 1.64]
-0.20 | 3.49 | 0.05 | [ 3.14, 3.88]
0.60 | 11.68 | 0.04 | [10.89, 12.53]
1.80 | 71.54 | 0.06 | [63.30, 80.87]
# trt = placebo
# V4 = 1
x | Predicted | SE | 95% CI
-----------------------------------------
-1.40 | 1.51 | 0.10 | [ 1.24, 1.84]
-0.80 | 2.66 | 0.08 | [ 2.28, 3.11]
-0.20 | 4.70 | 0.06 | [ 4.16, 5.32]
0.60 | 10.05 | 0.05 | [ 9.04, 11.17]
1.80 | 31.36 | 0.08 | [26.98, 36.46]
# trt = progabide
# V4 = 1
x | Predicted | SE | 95% CI
-----------------------------------------
-1.40 | 0.49 | 0.11 | [ 0.39, 0.60]
-0.80 | 1.20 | 0.09 | [ 1.01, 1.43]
-0.20 | 2.97 | 0.07 | [ 2.61, 3.40]
0.60 | 9.96 | 0.05 | [ 8.95, 11.08]
1.80 | 60.98 | 0.07 | [52.69, 70.58]
>
> glm2_p %>% as_tibble()
# A tibble: 68 x 7
x predicted std.error conf.low conf.high group facet
<dbl> <dbl> <dbl> <dbl> <dbl> <fct> <fct>
1 -1.4 1.77 0.0919 1.48 2.12 placebo 0
2 -1.4 1.51 0.101 1.24 1.84 placebo 1
3 -1.4 0.570 0.102 0.467 0.696 progabide 0
4 -1.4 0.486 0.110 0.392 0.603 progabide 1
5 -1.2 2.14 0.0839 1.81 2.52 placebo 0
6 -1.2 1.82 0.0933 1.52 2.19 placebo 1
7 -1.2 0.771 0.0936 0.642 0.926 progabide 0
8 -1.2 0.657 0.102 0.538 0.803 progabide 1
9 -1 2.58 0.0761 2.23 3.00 placebo 0
10 -1 2.20 0.0863 1.86 2.61 placebo 1
# … with 58 more rows
このように3つ目の説明変数も2つ目と同様にグループとして扱われます。ただし、2番目の説明変数に基づくグループ属性が列「group」に格納されるのに対し、3番目の説明変数に基づくグループ属性は列「facet」に格納されます。
このグループの値はaesのfacetに指定することでグループごとの図を作成できます。
plotで確認すると以下のようになります。
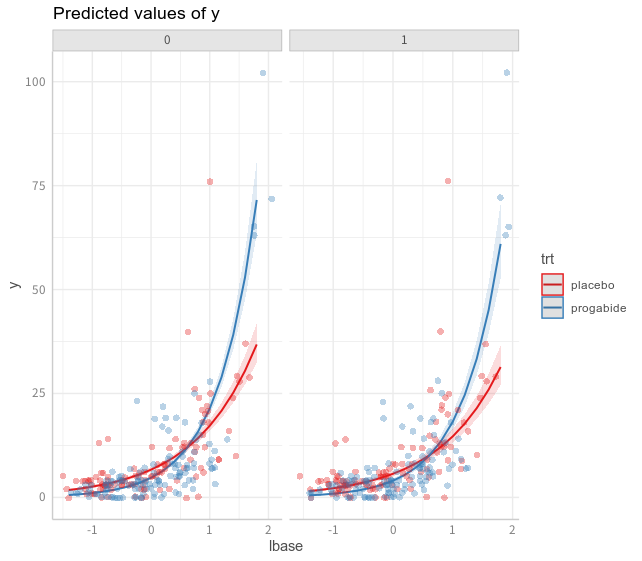
> plot(glm2_p, rawdata = T)
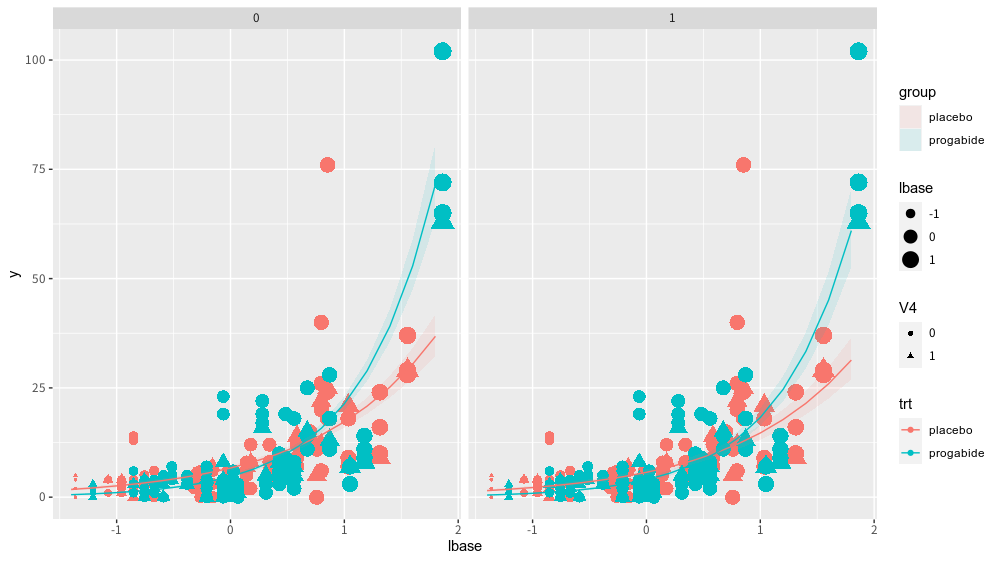
ggplot2で描画すると例えば以下のように出来ます。sizeでlbaseの値を、shapeでV4の値を視覚化しています。
> ggplot() +
+ geom_point(data = epil0, aes(x = lbase, y = y, color = trt, size = lbase, shape = V4)) +
+ geom_line(data = glm2_p, aes(x = x, y = predicted, color = group)) +
+ geom_ribbon(data = glm2_p, aes(x = x,ymin = conf.low, ymax = conf.high, fill = group), alpha = 0.1) +
+ facet_grid(~ facet)
今回はlageをconditionに指定しましたがtermsに指定することも出来ます。その場合はグループ属性が列「panel」に格納されるようです。5つ以上の場合は不明。
ただあまりにも複雑なプロットをすると見る側も疲れるので、4つ以上の説明変数があるモデルを使う際にはいくつかの説明変数の値をconditionで指定してやるのが良いと思います。
glmer
基本的な使い方はglmと変わらないのですが、glmerの場合にはランダム効果分散を考慮するかどうかでプロットが変わってきます。
ランダム効果分散を考慮しない場合
ランダム効果を考慮しない場合、type = "fe"を指定します。ランダム効果による変動は予測値の計算にあたり考慮されません。
見た目はglmの場合とほとんどかわりません。
> glmer1 <- glmer(y ~ lbase*trt + lage + V4 + (1 | subject), family = "poisson", data = epil0)
>
> (glmer1_p1 <- ggpredict(glmer1, type = "fe", terms = c("lbase", "trt", "V4"), condition = c(lage = mean(epil0$lage))))
# Predicted counts of y
# x = lbase
# trt = placebo
# V4 = 0
x | Predicted | SE | 95% CI
-----------------------------------------
-1.40 | 1.82 | 0.21 | [ 1.19, 2.76]
-0.80 | 3.08 | 0.15 | [ 2.29, 4.14]
-0.20 | 5.24 | 0.11 | [ 4.23, 6.49]
0.60 | 10.62 | 0.13 | [ 8.25, 13.68]
1.80 | 30.66 | 0.25 | [18.63, 50.47]
# trt = progabide
# V4 = 0
x | Predicted | SE | 95% CI
-----------------------------------------
-1.40 | 0.81 | 0.25 | [ 0.49, 1.33]
-0.80 | 1.68 | 0.17 | [ 1.20, 2.37]
-0.20 | 3.51 | 0.11 | [ 2.81, 4.38]
0.60 | 9.32 | 0.13 | [ 7.26, 11.97]
1.80 | 40.40 | 0.28 | [23.41, 69.70]
# trt = placebo
# V4 = 1
x | Predicted | SE | 95% CI
-----------------------------------------
-1.40 | 1.55 | 0.22 | [ 1.01, 2.37]
-0.80 | 2.63 | 0.16 | [ 1.94, 3.57]
-0.20 | 4.47 | 0.12 | [ 3.55, 5.61]
0.60 | 9.05 | 0.14 | [ 6.95, 11.80]
1.80 | 26.13 | 0.26 | [15.78, 43.29]
# trt = progabide
# V4 = 1
x | Predicted | SE | 95% CI
-----------------------------------------
-1.40 | 0.69 | 0.26 | [ 0.42, 1.14]
-0.80 | 1.44 | 0.18 | [ 1.01, 2.03]
-0.20 | 2.99 | 0.12 | [ 2.36, 3.79]
0.60 | 7.94 | 0.13 | [ 6.11, 10.33]
1.80 | 34.43 | 0.28 | [19.84, 59.75]
Adjusted for:
* subject = 0 (population-level)
Standard errors are on link-scale (untransformed).
>
> glmer1_p1 %>% as_tibble()
# A tibble: 68 x 7
x predicted std.error conf.low conf.high group facet
<dbl> <dbl> <dbl> <dbl> <dbl> <fct> <fct>
1 -1.4 1.82 0.214 1.19 2.76 placebo 0
2 -1.4 1.55 0.218 1.01 2.37 placebo 1
3 -1.4 0.809 0.253 0.492 1.33 progabide 0
4 -1.4 0.689 0.256 0.417 1.14 progabide 1
5 -1.2 2.17 0.192 1.49 3.15 placebo 0
6 -1.2 1.85 0.196 1.26 2.71 placebo 1
7 -1.2 1.03 0.226 0.664 1.61 progabide 0
8 -1.2 0.880 0.229 0.562 1.38 progabide 1
9 -1 2.58 0.170 1.85 3.61 placebo 0
10 -1 2.20 0.175 1.56 3.11 placebo 1
# … with 58 more rows
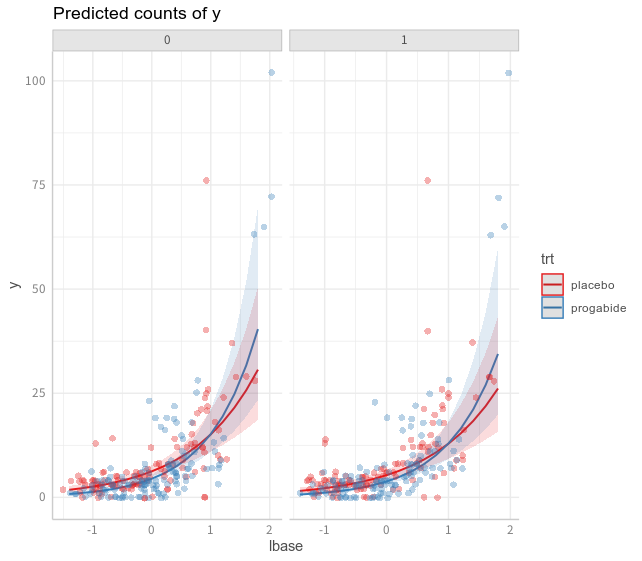
> plot(glmer1_p1, rawdata = T)
> ggplot() +
+ geom_point(data = epil0, aes(x = lbase, y = y, color = trt, size = lbase, shape = V4)) +
+ geom_line(data = glmer1_p1, aes(x = x, y = predicted, color = group)) +
+ geom_ribbon(data = glmer1_p1, aes(x = x,ymin = conf.low, ymax = conf.high, fill = group), alpha = 0.1) +
+ facet_grid(~ facet)
ランダム効果分散を考慮する場合
ランダム効果を考慮する場合にはterms = "re"を指定します。この場合でも、ランダム効果による変動が予測値の計算にあたり考慮されない点は同じです。
ランダム効果を考慮する場合に変わるのは信頼区間です。ランダム効果分散が考慮されるため信頼区間が広くなります。
> (glmer1_p2 <- ggpredict(glmer1, type = "re", terms = c("lbase", "trt", "V4"), condition = c(lage = mean(epil0$lage))))
# Predicted counts of y
# x = lbase
# trt = placebo
# V4 = 0
x | Predicted | SE | 95% CI
-----------------------------------------
-1.40 | 1.82 | 0.54 | [ 0.62, 5.28]
-0.80 | 3.08 | 0.52 | [ 1.11, 8.60]
-0.20 | 5.24 | 0.51 | [ 1.92, 14.32]
0.60 | 10.62 | 0.52 | [ 3.85, 29.28]
1.80 | 30.66 | 0.56 | [10.19, 92.24]
# trt = progabide
# V4 = 0
x | Predicted | SE | 95% CI
------------------------------------------
-1.40 | 0.81 | 0.56 | [ 0.27, 2.43]
-0.80 | 1.68 | 0.53 | [ 0.60, 4.76]
-0.20 | 3.51 | 0.51 | [ 1.28, 9.60]
0.60 | 9.32 | 0.52 | [ 3.38, 25.68]
1.80 | 40.40 | 0.57 | [13.13, 124.24]
# trt = placebo
# V4 = 1
x | Predicted | SE | 95% CI
----------------------------------------
-1.40 | 1.55 | 0.55 | [0.53, 4.51]
-0.80 | 2.63 | 0.52 | [0.94, 7.35]
-0.20 | 4.47 | 0.51 | [1.63, 12.24]
0.60 | 9.05 | 0.52 | [3.27, 25.04]
1.80 | 26.13 | 0.56 | [8.66, 78.84]
# trt = progabide
# V4 = 1
x | Predicted | SE | 95% CI
------------------------------------------
-1.40 | 0.69 | 0.56 | [ 0.23, 2.08]
-0.80 | 1.44 | 0.53 | [ 0.51, 4.07]
-0.20 | 2.99 | 0.52 | [ 1.09, 8.21]
0.60 | 7.94 | 0.52 | [ 2.87, 21.95]
1.80 | 34.43 | 0.57 | [11.16, 106.19]
Adjusted for:
* subject = 0 (population-level)
Standard errors are on link-scale (untransformed).
Intervals are prediction intervals.
>
> glmer1_p2 %>% as_tibble()
# A tibble: 68 x 7
x predicted std.error conf.low conf.high group facet
<dbl> <dbl> <dbl> <dbl> <dbl> <fct> <fct>
1 -1.4 1.82 0.545 0.624 5.28 placebo 0
2 -1.4 1.55 0.546 0.530 4.51 placebo 1
3 -1.4 0.809 0.561 0.269 2.43 progabide 0
4 -1.4 0.689 0.563 0.229 2.08 progabide 1
5 -1.2 2.17 0.537 0.757 6.20 placebo 0
6 -1.2 1.85 0.538 0.643 5.30 placebo 1
7 -1.2 1.03 0.550 0.352 3.03 progabide 0
8 -1.2 0.880 0.551 0.299 2.59 progabide 1
9 -1 2.58 0.529 0.916 7.29 placebo 0
10 -1 2.20 0.531 0.778 6.24 placebo 1
# … with 58 more rows
SEの値が大きくなっていることがわかると思います。
プロットすると以下のようになります。
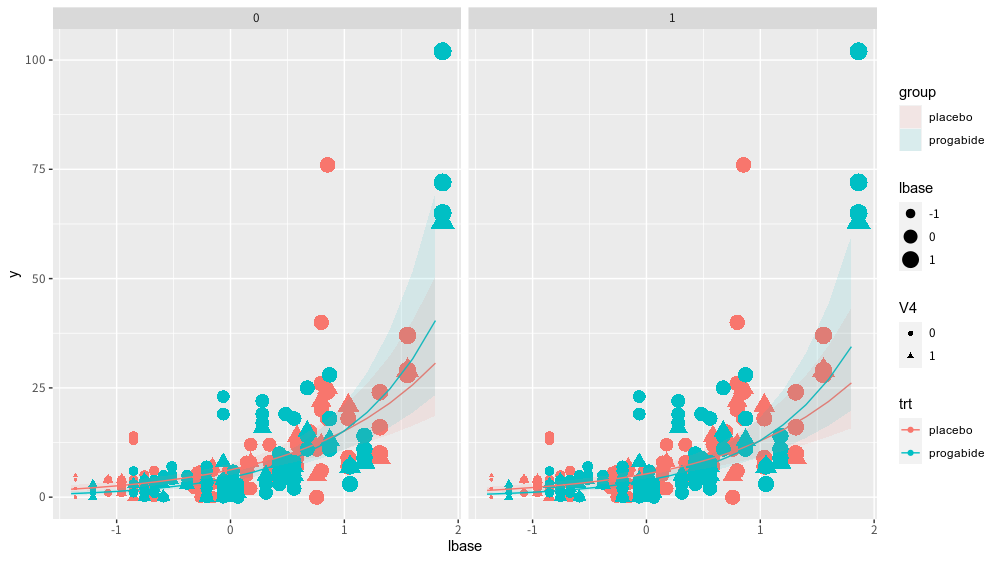
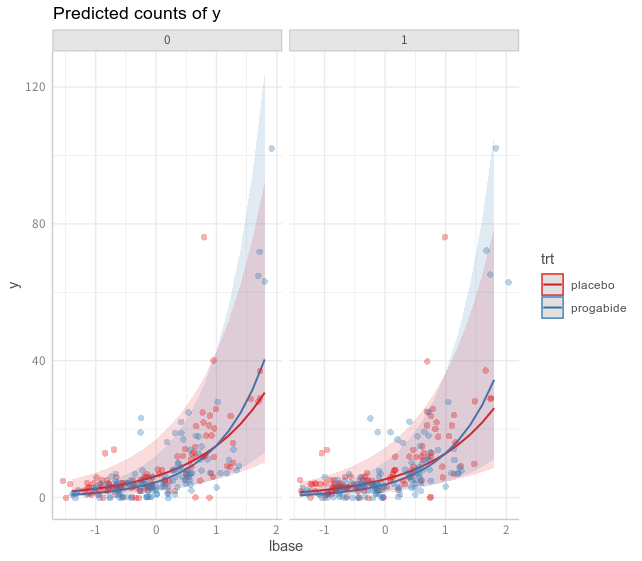
> plot(glmer1_p2, rawdata = T)
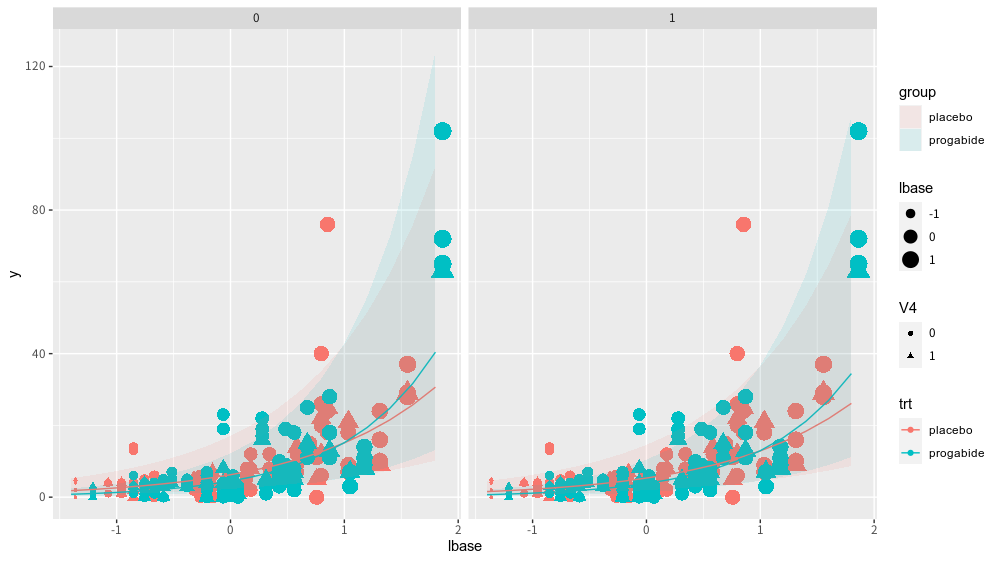
ggplot2で描画すると以下のようになります。
> ggplot() +
+ geom_point(data = epil0, aes(x = lbase, y = y, color = trt, size = lbase, shape = V4)) +
+ geom_line(data = glmer1_p2, aes(x = x, y = predicted, color = group)) +
+ geom_ribbon(data = glmer1_p2, aes(x = x,ymin = conf.low, ymax = conf.high, fill = group), alpha = 0.1) +
+ facet_grid(~ facet)
ランダム効果ごとの回帰線を見たい場合(非推奨)
公式ドキュメントによると非推奨な使い方のようなので、あくまで確認に使うのが良いと思います。
termsでランダム効果に使用した変数を指定するとランダム効果ごとの回帰線を描くことができます。
ただし信頼区間は描画されないようです。ランダム効果のグループ数によっては図が重くなるので注意。
> glmer1_p3 <- ggpredict(glmer1, type = "re", terms = c("lbase", "trt", "subject"), condition = c(lage = mean(epil0$lage), V4 = 0))
> ## 長すぎるのでコンソール出力は省略
>
> glmer1_p3 %>% as_tibble()
# A tibble: 2,006 x 4
x predicted group facet
<dbl> <dbl> <fct> <fct>
1 -1.4 1.92 placebo 1
2 -1.4 1.94 placebo 2
3 -1.4 2.54 placebo 3
4 -1.4 2.12 placebo 4
5 -1.4 1.85 placebo 5
6 -1.4 1.48 placebo 6
7 -1.4 1.61 placebo 7
8 -1.4 2.78 placebo 8
9 -1.4 1.51 placebo 9
10 -1.4 4.65 placebo 10
# … with 1,996 more rows
plotで描画すると以下のようになります。
> plot(glmer1_p3, rawdata = T)
解析結果を図示する際には何を示したいかを明確にすることが大事です。
それを踏まえてこのパッケージを使えば、効果的な図を作成できると思います!
easystats系関連記事
- glmとかglmerとかの結果を表形式で表示&CSVで出力 (easystats)
- glmやglmerのR2、多重共線性、正規性、過分散、ゼロ過剰を確認する (easystats)
- glmやglmerによるパラメータ推定値と信頼区間をggplot2で描画する (easystats)
参考
ggeffects: Marginal Effects of Regression Models - ggeffects
Reference - ggeffects
Introduction: Marginal Effects for Random Effects Models - ggeffects
ggeffects - Estimated Marginal Means and Marginal Effects from Regression Models - ggeffects
plot()-method - ggeffects
回帰分析の解釈と限界効果
strengejacke/ggeffects - GitHub
現代日本論演習/比較現代日本論研究演習 III「実践的統計分析」第13講 一般線型モデルのまとめ
Extension of Nakagawa & Schielzeth's R 2GLMM to random slopes models