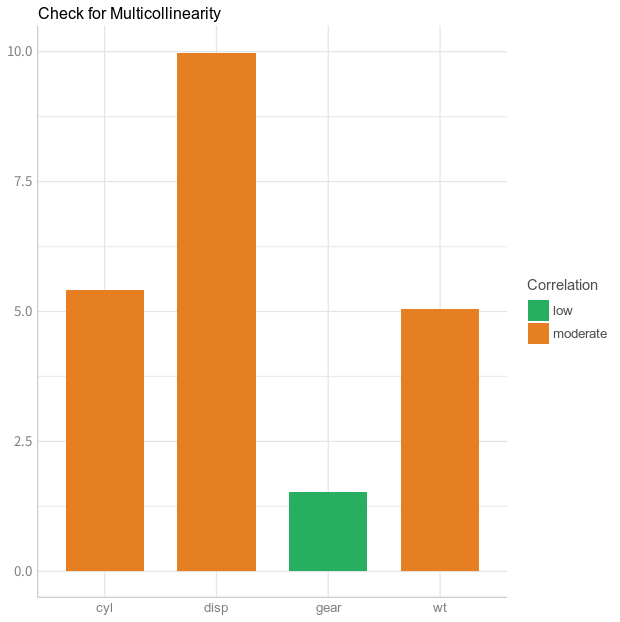モデルの品質(model quality)のチェック
一般化線形モデルや一般化線形混合モデルのパラメータ推定をRで行う場合、よく用いられるのはglmやglmer(lmer)だと思います。
これらの関数による解析結果の妥当性を評価するために、タイトルに上げたようないくつかの事項を確認したい場合があります。
AICや対数尤度を確認するのとは異なり、これらを確認するにはオブジェクトからデータを抽出したりパッケージを使い分けたりする必要があります。よって結構面倒です。
しかしeasystatsパッケージ群に含まれるperformanceパッケージを使うとかなり簡単にこれらの事項を確認できます。ここではその一例を紹介したいと思います。
※ 指標や検定について詳しい説明はしません(統計は勉強中なので踏み込んだ説明が出来ません。ごめんなさい)。あくまでパッケージの紹介と手順の確認のためのメモとして見てもらえればと思います。
※ 指標の根拠や算出方法については、performanceパッケージのマニュアル(あるいはレファレンス)やGitHubにあるソースコードで確認できます。レポート等に使用されたい方はそちらを参照してください。
インストール
CRANとGitHubどちらからでもインストールできます。GitHubは更新が速いので安定版を使いたいのであればCRANのほうがおすすめです。
- CRAN
以下のコマンドでインストールできます。
install.packages("performance")
- GitHub
easystatsごとインストールすることでインストールできます。
remotes::install_github("easystats/easystats")
すでにeasystatsに含まれるパッケージを部分的にインストールしている場合には、依存関係関連でエラーや警告が出たりします。そのため上記コマンドを実行する前にいったんそれらをアンインストールしたほうが良いです。
各事項の確認
ここでは以下のパッケージを使用します。
library(performance)
library(MASS)
library(lme4)
library(glmmTMB)
テストデータ、テストコードについては各パッケージのヘルプを参考にしました。一部エラーが出ていますが、例示としては問題ないのでそのままにしてあります。
R2の確認
performanceパッケージでは総称的関数であるr2で各モデルに対する適切な決定係数(あるいは疑似決定係数)を計算できます。
各モデルに対応するR2は以下のようになっています:
- 線形モデル:R2および調整済みR2
- 一般化線形モデル:Nagelkerke’s R2
- ロジスティックモデル:Tjur’s R2
- 混合モデル:Nakagawa’s R2
lm
> rm1 <- lm(mpg ~ wt + cyl + gear + disp, data = mtcars)
> r2(rm1)
# R2 for Linear Regression
R2: 0.835
adj. R2: 0.811
glm
> rm2 <- glm(Days ~ Sex/(Age + Eth*Lrn), data = quine, family = "poisson")
> r2(rm2)
$R2_Nagelkerke
Nagelkerke's R2
0.9905114
> # ロジスティックモデル
> rm3 <- glm(cbind(incidence, size - incidence) ~ period, family = binomial, data = cbpp)
> r2(rm3)
$R2_Tjur
Tjur's R2
0.001039836
glmer
> # 一般化線形混合モデル
> rm4 <- glmer(cbind(incidence, size - incidence) ~ period + (1 | herd), family = binomial, data = cbpp)
> r2(rm4)
# R2 for Mixed Models
Conditional R2: 0.187
Marginal R2: 0.085
多重共線性の確認
performanceパッケージでは多重共線性の指標の一つであるVIF統計量をcheck_collinearityで確認できます。
各パラメータに対するVIFの値が示されると同時に、棒グラフで値が可視化できます。VIF<5の場合低い相関、5≤VIF≤10の場合中程度の相関、10<VIFの場合高い相関とみなされます。
参照:Check for multicollinearity of model terms
glm
> cm1 <- glm(mpg ~ wt + cyl + gear + disp, data = mtcars, family = "gaussian")
> co1 <- check_collinearity(cm1)
> co1
# Check for Multicollinearity
Low Correlation
Parameter VIF Increased SE
gear 1.53 1.24
Moderate Correlation
Parameter VIF Increased SE
wt 5.05 2.25
cyl 5.41 2.33
disp 9.97 3.16
> plot(co1)
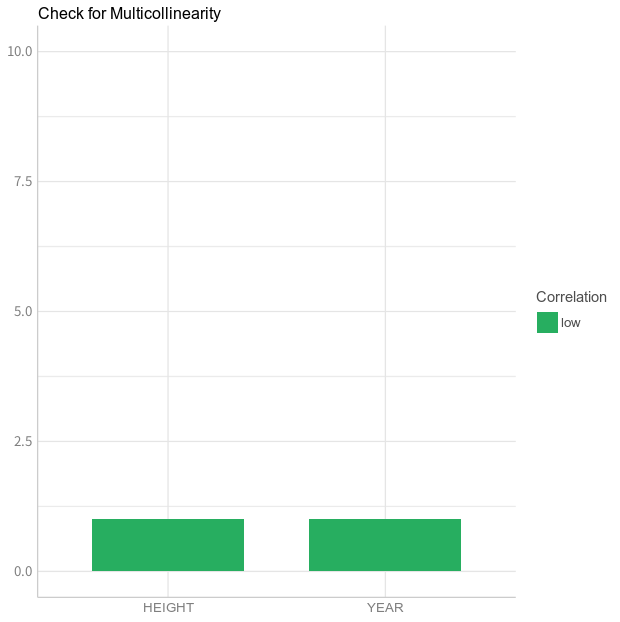
glmer
> form <- TICKS ~ YEAR + HEIGHT + (1|BROOD) + (1|INDEX) + (1|LOCATION)
> cm2 <- glmer(form, family = "poisson", data = grouseticks)
警告メッセージ:
checkConv(attr(opt, "derivs"), opt$par, ctrl = control$checkConv, で:
Model is nearly unidentifiable: very large eigenvalue
- Rescale variables?;Model is nearly unidentifiable: large eigenvalue ratio
- Rescale variables?
> co2 <- check_collinearity(cm2)
> co2
# Check for Multicollinearity
Low Correlation
Parameter VIF Increased SE
YEAR 1.00 1.00
HEIGHT 1.00 1.00
> plot(co2)
正規性の確認
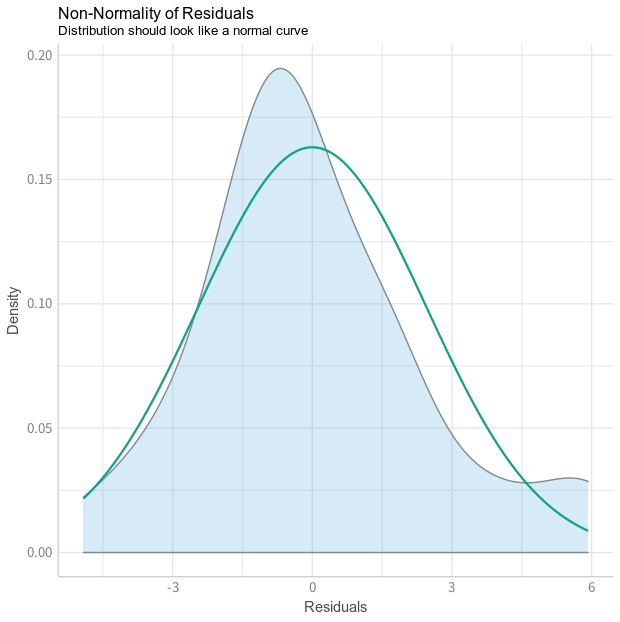
performanceパッケージでは残差の正規性をcheck_normalityで確認できます。
標準化された残差に対してシャピロ検定が実行されます。lmあるいはglmの結果に対してのみ使えます。
参照:Check model for (non-)normality of residuals.
> nm <- glm(mpg ~ wt + cyl + gear + disp, data = mtcars, family = "gaussian")
> no <- check_normality(nm)
OK: Residuals appear as normally distributed (p = 0.230).
> plot(no)
過分散の確認
performanceパッケージではcheck_overdispersionで過分散を確認できます。
過分散の指標としてピアソン残差の2乗和に対するカイ二乗検定の結果が示されます。dispersion rateは期待値との比、Pearson's Chi-Squaredはピアソン残差の2乗和、p-valueはp値です。確率分布がポアソン分布になっているモデルが対象です。
サンプル数(正確には残差自由度)が十分大きい場合に、あくまで過分散のラフな指標として使用可能とのことです(参考)。
ピアソン残差:pr_i = \frac{(y_i - \hat{\mu}_i)}{\sqrt{\hat{V}_i}}\quad (y_i:観測iにおける観測値;\quad \hat{\mu}_i:観測iにおける予測値;\quad \hat{V}_i:観測iにおける予測値の分散)
(参考)
※ ピアソン残差の2乗和が自由度=残差自由度のカイ二乗分布に従うことを利用しているのですが、上記の参考を見てもいまいち導出過程がわかりませんでした。
参照:Check overdispersion of GL(M)M's
glm
> po1 <- glm(Days ~ Sex/(Age + Eth*Lrn), data = quine, family = "poisson")
> check_overdispersion(po1)
# Overdispersion test
dispersion ratio = 10.534
Pearson's Chi-Squared = 1390.436
p-value = < 0.001
Overdispersion detected.
glmer
> form <- TICKS ~ YEAR + HEIGHT + (1|BROOD) + (1|INDEX) + (1|LOCATION)
> po2 <- glmer(form, family = "poisson", data = grouseticks)
警告メッセージ:
checkConv(attr(opt, "derivs"), opt$par, ctrl = control$checkConv, で:
Model is nearly unidentifiable: very large eigenvalue
- Rescale variables?;Model is nearly unidentifiable: large eigenvalue ratio
- Rescale variables?
> check_overdispersion(po2)
# Overdispersion test
dispersion ratio = 0.412
Pearson's Chi-Squared = 163.211
p-value = 1
No overdispersion detected.
ゼロ過剰の確認
performanceパッケージではcheck_zeloinflationでモデルのゼロ過剰を確認できます。
実際の0の数とモデルから期待される0の数、およびその比が示されます。こちらも確率分布がポアソン分布になっているモデルが対象です。
参照:Check for zero-inflation in count models
glm
> zi1 <- glm(count ~ spp + mined, family = "poisson", data = Salamanders)
> check_zeroinflation(zi1)
# Check for zero-inflation
Observed zeros: 387
Predicted zeros: 298
Ratio: 0.77
Model is underfitting zeros (probable zero-inflation).
glmer
> zi2 <- glmer(count ~ spp + mined + (1|site), family = "poisson", data = Salamanders)
> check_zeroinflation(zi2)
# Check for zero-inflation
Observed zeros: 387
Predicted zeros: 311
Ratio: 0.80
Model is underfitting zeros (probable zero-inflation).
備考
自己相関を確認するcheck_autocorrelationもあるのですが、これはデータに順序があると仮定してダービーワトソン検定を行うもののようです。残差がAR(1) かどうかを確認するためのものなので注意が必要です。
参照:Check model for independence of residuals.
performanceパッケージはglmmTMB等の他のパッケージの関数にも対応しています。
また収束や外れ値などの確認もできるので気になる方は確認してみてください。
参考
- easystatsについて①: パッケージ群の紹介
- Package ‘performance’
- easystats/performance
- performance: Test if your model is a good model!
- Compute R2s and other performance indices for all your models!
- Check your (Mixed) Model for Multicollinearity with 'performance'
- GLMM FAQ
- Modern Applied Statistics with S
- Package ‘lme4’
- Package ‘glmmTMB’
- DURBIN-WATSON 検定
- ダービン・ワトソン検定