既存投稿一覧ページへのリンク
Before
Next
C問題
この問題はフィボナッチ数列の変形問題かな?と思ったら、タイトルにk階フィボナッチって書いてあった。
入力例01
正整数 $N = 4$, $K = 2$ が与えられます。長さ $N+1 = 5$ の数列 $A = (A_0, A_1, A_2, A_3, A_4)$ の各要素の値を、以下の方法で定義します。
- $0 \leq i < 2$ のとき、$A_i = 1$
- $2 \leq i$ のとき、$A_i = A_{i-2} + A_{i-1}$
このとき、$A_4$ を $10^9$ で割ったあまりを求めてください。
- $A_0 = 1$
- $A_1 = 1$
- $A_2 = A_0 + A_1 = 1 + 1 = 2$
- $A_3 = A_1 + A_2 = 1 + 2 = 3$
- $A_4 = A_2 + A_3 = 2 + 3 = 5$
よって、$A_4 = 5$ となります。
input
4 2
input_python
def io_func():
# 標準入力から1行読み込み、空白区切りで整数として取得
n, k = map(int, input().split())
# 取得した値を戻り値として返す(タプルでまとめる)
return n, k
output
5
D問題
入力例01
長さ4の文字列Sが「o???」として与えられる。ここで、Sの文字は「.」「o」「?」のみからなる。
「?」の各文字を「.」または「o」で自由に置き換えてできるすべての文字列のうち、以下の2つの条件の両方を満たすものの集合をXとする:
- 「o」の個数がちょうど2個である。
- 「o」が隣り合わない。
なお、Xが空集合にならないことは保証されている。
次に、Xに含まれるすべての文字列について、それらの各i番目(1≦i≦4)の文字がすべて「.」になる場合はTi=「.」、すべて「o」になる場合はTi=「o」、両方存在する場合はTi=「?」としたとき、長さ4の文字列Tを出力しなさい。
直感的には、oにのみ着目すれば解けそうな気がする。
input
4 2
o???
input_python
def io_func():
# 標準入力からNとKを取得(整数として分割して格納)
n, k = map(int, input().split())
# 標準入力から文字列Sを取得し、リストとして格納
s = list(input())
# 複数の変数をタプルで返す
return n, k, s
output
o.??
E問題
入力例01
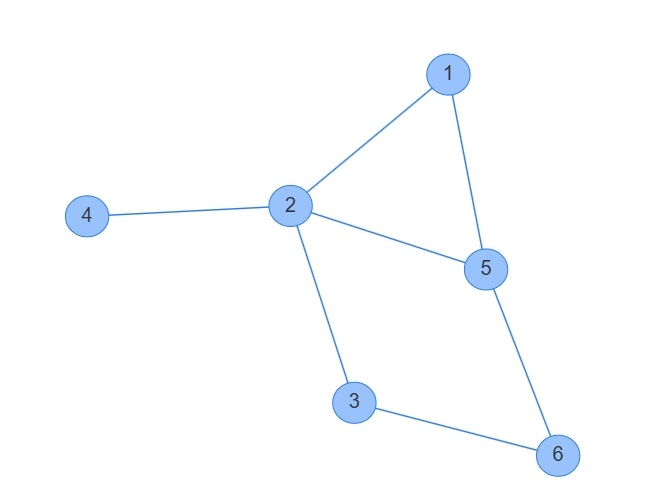
頂点数 6、辺数 7 の無向グラフがあります。
各頂点には 1, 2, 3, 4, 5, 6 の番号がついています。
また、次の 7 本の辺があります:
- 頂点 1 と 頂点 2 を結ぶ辺
- 頂点 1 と 頂点 5 を結ぶ辺
- 頂点 2 と 頂点 3 を結ぶ辺
- 頂点 2 と 頂点 4 を結ぶ辺
- 頂点 2 と 頂点 5 を結ぶ辺
- 頂点 3 と 頂点 6 を結ぶ辺
- 頂点 5 と 頂点 6 を結ぶ辺
それぞれ k = 1, 2, 3, 4, 5, 6 について、次の問いに答えてください。
次の操作について考える。
- 頂点を一つ選ぶ。選んだ頂点と、その頂点に接続する全ての辺をグラフから削除する。
上記の操作を繰り返すことで、次の条件を満たすことができるか判定してください。- 頂点 1 から辺をたどって到達できる頂点の集合が、「ちょうど 頂点 1, 2, ..., k の合計 k 個」からなる。
可能な場合、条件を満たすには最小で何回の操作が必要か、求めてください。
input
6 7
1 2
1 5
2 3
2 4
2 5
3 6
5 6
input_python
def io_func():
# n, m を入力(頂点数と辺数)
n, m = map(int, input().split())
# 空の隣接リストgを初期化
g = [[] for _ in range(n)]
# m回、辺の接続情報を読み込み
for _ in range(m):
u_str, v_str = input().split()
u, v = int(u_str) - 1, int(v_str) - 1 # 0-indexedに変換
g[u].append(v)
g[v].append(u)
return n, m, g # 頂点数・辺数・隣接リストを返す
output
2
3
3
2
1
0
F問題
入力例01
頂点に 1 から 3 までの番号が付いた 3 頂点の木 1 と、頂点に 1 から 3 までの番号が付いた 3 頂点の木 2 がそれぞれ次のように与えられます。
-
木 1 の辺:
1 と 3 を結ぶ
1 と 2 を結ぶ -
木 2 の辺:
1 と 2 を結ぶ
3 と 1 を結ぶ
木 1 の i 番目の頂点と、木 2 の j 番目の頂点を双方向に辺で結ぶと、1 つの木が得られます。この木の直径を f(i, j) と定めます。
全ての i (1 ≦ i ≦ 3) および j (1 ≦ j ≦ 3) について、$\sum_{i=1}^{3}\sum_{j=1}^{3} f(i,j)$を求めてください。
ただし、木の 2 頂点間の距離は一方から他方へ移動するとき通過する辺の本数の最小値とし、木の直径は任意の 2 頂点間の距離の最大値とします。
-
木1:
1—2
|
3 -
木2:
1—2
|
3
全組み合わせ
| i | j | 結ぶ位置 | 直径 |
|---|---|---|---|
| 1 | 1 | 中心-中心 | 3 |
| 1 | 2 | 中心-端 | 4 |
| 1 | 3 | 中心-端 | 4 |
| 2 | 1 | 端-中心 | 4 |
| 2 | 2 | 端-端(隣) | 5 |
| 2 | 3 | 端-端(遠) | 5 |
| 3 | 1 | 端-中心 | 4 |
| 3 | 2 | 端-端(遠) | 5 |
| 3 | 3 | 端-端(隣) | 5 |
愚直に解くと、TLEするでしょうね・・・
input
3
1 3
1 2
3
1 2
3 1
input_python
def io_func():
# 1つ目の木の読み込み
n = int(input()) # 頂点数Nを取得
d_list = [[] for _ in range(n)] # 隣接リスト初期化
for _ in range(n - 1):
u, v = map(int, input().split()) # 辺情報取得
u -= 1; v -= 1 # 0-indexedに変換
d_list[u].append(v)
d_list[v].append(u)
# 2つ目の木の読み込み
m = int(input()) # 頂点数Mを取得
d_list2 = [[] for _ in range(m)] # 隣接リスト初期化
for _ in range(m - 1):
u, v = map(int, input().split()) # 辺情報取得
u -= 1; v -= 1 # 0-indexedに変換
d_list2[u].append(v)
d_list2[v].append(u)
# 変数: n,m:頂点数, d_list,d_list2:隣接リストを返却
return n, d_list, m, d_list2
output
39