◆目次:ディープラーニングを基本から学ぶ
◆次章:Part2 ニューラルネットワークの学習
■1.ニューラルネットワークの基本
▼1.1.ニューラルネットワークとは?
脳機能に見られるいくつかの特性を計算機上のシミュレーションによって表現することを目指した数学モデルである。
WikiPediaより
これにより、コンピューターに学習能力を持たせようとするアプローチである。
ディープラーニングで一般的に用いられるモデルであり、分類問題と回帰問題の両方に用いることができる。
▼1.2.パーセプトロン
ローゼンブラットというアメリカの研究者によって1957年に考案されたアルゴリズム。
ニューラルネットワークの起源となるアルゴリズムである。
パーセプトロンは複数の信号(流す 1/流さない 0 の二値)を入力として受け取り、一つの信号を出力する。
例えば、2つの入力信号を受け取り、yを出力するパーセプトロンは以下の式で表される。
y = \left\{
\begin{array}{}
0 & (b + w_1x_1 + w_2x_2 \leqq 0) \\
1 & (b + w_1x_1 + w_2x_2 > 0) \\
\end{array}
\right. \\
ここで、$y:出力信号、x_1、x_2:入力信号、w_1、w_2:重み、b:バイアス$である。
入力信号ごとに重み付けをし、その総和に対してバイアスを足すことで出力信号を得る。
バイアスにより出力信号の発火しやすさをコントロールする。
▼1.3.活性化関数
入力信号の総和を出力信号に変換する関数のことを言う。
活性化関数は入力信号の総和がどのような条件の時に発火する(=出力信号に影響を与える)かを決定する役割を担っている。
▽1.3.1.ステップ関数
パーセプトロンで用いられる活性化関数。
閾値を境にして出力が変わる。
h(x) = \left\{
\begin{array}{}
0 & (x \leqq 0) \\
1 & (x > 0) \\
\end{array}
\right. \\
pythonで実装すると以下のようになる。
def step_function(x):
if(x > 0):
return 1
else:
return 0
ただし、ディープラーニングで扱うのは行列なので、実用的には以下のようになる。
import numpy as np
def step_function(x):
return np.array(x > 0, dtype=np.int)
np.array(x > 0, dtype=np.int)
は、 x > 0 の評価結果(true/false)をint型(1/0)にした行列という意味。
例えば、
x = [1, -1, 5]
であれば戻り値は
[1, 0, 1]
になる。
▽1.3.2.シグモイド関数
ニューラルネットワークで昔からよく用いられる活性化関数の一つ
h(x) = {\frac{1}{1 + \exp(-x)}}
exp(-x)は$e^{-x}$を意味する。
pythonで実装すると以下のようになる。
import numpy as np
def sigmoid(x):
return 1 / (1 + np.exp(-x))
▽1.3.3.ReLU関数
ReLU(Rectified Linear Unit)
ニューラルネットワークで最近用いられるようになった活性化関数。
h(x) = \left\{
\begin{array}{}
x & (x > 0) \\
0 & (x \leqq 0) \\
\end{array}
\right. \\
pythonで実装すると以下のようになる。
import numpy as np
def relu(x):
return np.maximum(0, x) # 0とxで大きいほうの値を返す
▼1.4.出力層で用いられる活性化関数
出力層の活性化関数は分類問題(データがどこに属するか分類する)、回帰問題(データの具体的な数値を予測する)のどちらに用いるかで変更する必要がある。
回帰問題では恒等関数を、分類問題ではソフトマックス関数を用いるのが一般的である。
▽1.4.1.恒等関数
恒等関数は、入ってきたものに対して何も手を加えずに出力する関数である。
そのため、出力層で恒等関数を用いると、入力信号をそのまま出力するだけになる。
▽1.4.2.ソフトマックス関数
y_k = {\frac{exp(a_k)}{\sum_{i=1}^n exp(a_i)}}
ここで、$y_k:k番目の出力信号、a_k:k番目の入力信号$である。
このようにソフトマックス関数の分子はある1つの入力信号の指数関数、分母は全ての入力信号の指数関数の和から構成される。
また、ソフトマックス関数の出力は0~1.0の実数となり、出力の総和は1になる。
この特徴により、ソフトマックス関数の出力を確率として解釈することができる。
import numpy as np
def softmax(a):
c = np.max(a)
exp_a = np.exp(a - c) # オーバーフロー対策
sum_exp_a = np.sum(exp_a)
y = exp_a /sum_exp_a
return y
下記の部分だが
exp_a = np.exp(a - c) # オーバーフロー対策
指数関数の計算の場合、値が大きくなりすぎデータ幅に収まりきらなくなり、オーバーフローを起こす場合があり、その対策として何らかの定数を引くことでオーバーフローを防ぐようにする。
▼1.5.ニューラルネットワークの実装
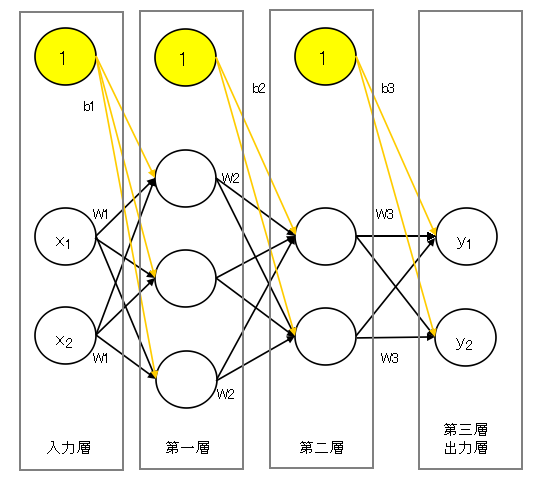
ここまでの復習として、3層からなるニューラルネットワークを実装する。
$x_1, x_2:入力信号、y_1, y_2:出力信号$
$W_1, W_2, W_3:重み$
$b_1, b_2, b_3:バイアス$
▽1.5.1.3層ニューラルネットワークの実装
入力層→第一層、第一層→第二層への活性化関数にはシグモイド関数を、
第二層→出力層への活性化関数は恒等関数を用いることとする。
これは、あくまで例であり、実例ではそのニューラルネットワークに合った活性化関数を用いる。
# coding: utf-8
import numpy as np
# シグモイド関数
def sigmoid(x):
return 1 / (1 + np.exp(-x))
# 恒等関数
def identity_function(x):
return x
# 各層の重み、バイアスの設定
def init_network():
network = {}
# 入力層→第一層への重み
network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
# 入力層→第一層へのバイアス
network['b1'] = np.array([0.1, 0.2, 0.3])
# 第一層→第二層への重み
network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
# 第一層→第二層へのバイアス
network['b2'] = np.array([0.1, 0.2])
# 第二層→出力層への重み
network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]])
# 第二層→出力層へのバイアス
network['b3'] = np.array([0.1, 0.2])
return network
# 入力から出力方向への伝達処理
def forword(network, x):
W1, W2, W3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
# 入力層→第一層への伝達
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1) # シグモイド関数
# 第一層→第二層への伝達
a2 = np.dot(z1, W2) + b2
z2 = sigmoid(a2) # シグモイド関数
# 第二層→出力層への伝達
a3 = np.dot(z2, W3) + b3
y = identity_function(a3) # 恒等関数
return y
# メイン部分
network = init_network()
x = np.array([1.0, 0.5]) # 入力信号
y = forword(network, x)
print(y)
これを理解するには多次元配列の計算を理解することが必要となる。
a1 = np.dot(x, W1) + b1
こちらを実値で表すと
\begin{pmatrix}
1.0 & 0.5
\end{pmatrix}
\times
\begin{pmatrix}
0.1 & 0.3 & 0.5 \\
0.2 & 0.4 & 0.6
\end{pmatrix}
+
\begin{pmatrix}
0.1 & 0.2 & 0.3
\end{pmatrix}
\\
=
\begin{pmatrix}
1.0 \times 0.1 + 0.5 \times 0.2 & 1.0 \times 0.3 + 0.5 \times 0.4 & 1.0 \times 0.5 + 0.5 \times 0.6 )
\end{pmatrix}
+
\begin{pmatrix}
0.1 & 0.2 & 0.3
\end{pmatrix}
\\
=
\begin{pmatrix}
0.2 & 0.5 & 0.8
\end{pmatrix}
+
\begin{pmatrix}
0.1 & 0.2 & 0.3
\end{pmatrix}
\\
=
\begin{pmatrix}
0.3 & 0.7 & 1.1
\end{pmatrix}
となる。
▽1.5.2.バッチ処理で高速化する
バッチ処理にすることにより処理を高速化することができます。
ニューラルネットワークでは、複数の入力データを束(バッチ)にしてまとめて処理することをバッチ処理と呼ぶ。
1.5.1 で示したソースコードで入力データは、
x = np.array([1.0, 0.5]) # 入力信号
であるが、これが束になるので
x = np.array([[1.0, 0.5], [2.0, 1.0], [4.2, 0.3]]) # 入力信号
のようになる(これは3つの入力データを束ねたもの)
出力データも、入力データに合わせた形状になる。
[ 0.31682708 0.69627909] # 入力データ1つ
[[ 0.31682708 0.69627909]
[ 0.32303088 0.71009755]
[ 0.32610891 0.71698491]] # 入力データ3つ
バッチ処理を行うことで大きな配列の計算を行うことになるが、大きな配列を一度に計算する方が、分割した小さい配列を少しずつ計算するよりも早く計算が完了する。