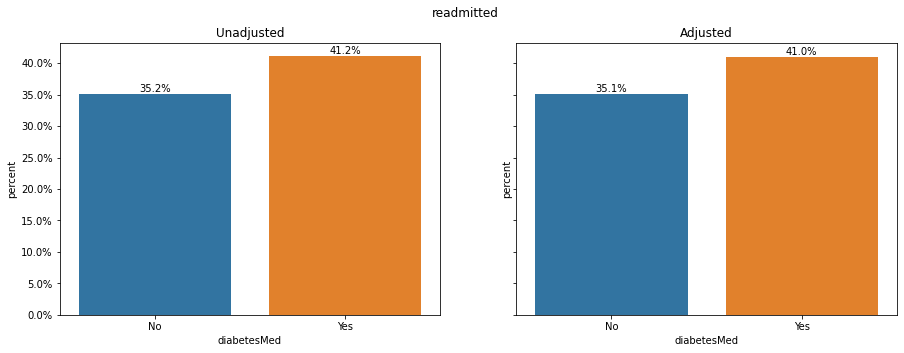【DataRobot】解説！AIアクセラレーター ～Use Causal AI with DataRobot編～

はじめに

はじめまして。社内でデータサイエンティストを務めております@nttd-tamurayucです。

NTTデータ デザイン＆テクノロジーコンサルティング事業本部では、お客様企業のAI・データ活用を、コンサルティングから基盤構築、実行支援を通じた成果創出までワンストップで創出しており、その支援テクノロジーの一つとして DataRobot を提供しております。

本記事では、DataRobot社が提供するコンテンツであるAIアクセラレータより「Use Causal AI with DataRobot（DataRobotを用いたCausal AI）」について解説したいと思います。

DataRobotとは

DataRobot社は、人工知能（AI）に対するユニークなコラボレーション型のアプローチであるバリュー・ドリブン AIのリーダーです。

DataRobot社の製品であるDataRobotは、自動機械学習（AutoML）プラットフォームであり、機械学習モデルの構築、トレーニング、評価、デプロイメントを自動化することができます。複雑なデータ分析を迅速かつ簡単に実行し、優れた予測モデルの作成をサポートすることが可能です。

AIアクセラレーターとは

AIアクセラレーターは、DataRobot社によって提供されているコンテンツの一つで、機械学習プロジェクトの構築と提供を成功させるためのデータサイエンスの専門知識を、反復可能なコードファーストのワークフローとモジュール化されたビルディングブロックに体系化してパッケージ化したものです。

【解説】Causal AI with DataRobot

以降では、AIアクセラレータの中で提供されているコンテンツの一つである「Causal AI with DataRobot」の解説を実施します。

補足
ご自身の環境で同様の分析を実施される場合、こちらよりパッケージをDLしてください。

Predictive AI vs Causal AI

Causal AI(因果関係AI)を説明する前に、一般的な予測AI(Predictive AI)について説明します。

予測AIとは、大量のデータを学習して未来の結果やトレンドを予測する技術のことを指します。機械学習や深層学習などの技術を用いて、過去のデータパターンから未来の出来事を予測します。
予測AIは、観測変数間の微妙な予測関係を明らかにする強力なツールですが、場合によっては2つの変数間の因果関係について結論を導き出す必要があります。

こうした問題を解決する手法として、Causal AIがあります。Causal AIは、予測だけでなく、事象間の因果関係を理解するAIのことを指します。これは、ある事象が別の事象を引き起こす理由を説明し、その結果を予測することを可能にします。
Causal AIは、ただデータに基づいた予測を行なうだけでなく、"なぜ"その予測が成り立つのかという因果関係を明らかにします。この技術は、データ駆動型の意思決定をより強力にし、より正確な予測と戦略的洞察を提供します。

分析テーマ

糖尿病患者の再入院結果を記録したデータを用いて、患者の薬物治療状況と再入院の可能性との間の因果関係を評価します。

Step1. 設定

分析の開始にあたり、以下の設定を実行します。

1. ライブラリのインポート
2. DataRobotへの接続
3. データの読み込み
4. 可視化（オプション）

ライブラリのインポート

from io import BytesIO
import os

import datarobot as dr
import matplotlib.pyplot as plt
from matplotlib.ticker import PercentFormatter
import pandas as pd
import seaborn as sns

DataRobotへの接続

dr.Client()

<datarobot.rest.RESTClientObject at 0x7fa7bed4d610>

DataRobotへの接続方法の詳細については、こちらのドキュメントを参照ください.

データの読み込み

今回利用するデータセットは、以下の研究論文で使用されたデータを修正（行と列の数を削減）したものです。

Strack, B., DeShazo, J. P., Gennings, C., Olmo, J. L., Ventura, S., Cios, K. J., & Clore, J. N. (2014). Impact of HbA1c measurement on hospital readmission rates: analysis of 70,000 clinical database patient records. BioMed research international, 2014, 781670. https://doi.org/10.1155/2014/781670

working_df = pd.read_csv("storage/diabetes_subset.csv")
working_df

	readmitted	race	gender	age	weight	admission_type_id	admission_source_id	number_inpatient	medical_specialty	num_lab_procedures	number_diagnoses	num_medications	time_in_hospital	diabetesMed
0	False	Caucasian	Female	[50-60)	?	Elective	Physician Referral	0	Surgery-Neuro	35	9	21	1	No
1	False	Caucasian	Female	[20-30)	[50-75)	Urgent	Physician Referral	0	?	8	6	5	2	No
2	True	Caucasian	Male	[80-90)	?	Not Available	NaN	1	Family/GeneralPractice	12	9	21	7	Yes
3	False	AfricanAmerican	Female	[50-60)	?	Emergency	Transfer from another health care facility	0	?	33	3	5	4	Yes
4	False	AfricanAmerican	Female	[50-60)	?	Emergency	Emergency Room	0	Psychiatry	31	7	13	5	Yes
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
9995	False	Caucasian	Female	[60-70)	?	Elective	Physician Referral	0	?	30	7	29	3	Yes
9996	False	AfricanAmerican	Male	[60-70)	?	Urgent	Emergency Room	0	Emergency/Trauma	1	9	15	8	Yes
9997	True	AfricanAmerican	Female	[70-80)	?	Emergency	Emergency Room	1	InternalMedicine	46	6	14	13	No
9998	False	Caucasian	Male	[80-90)	?	Urgent	Emergency Room	3	InternalMedicine	62	9	7	2	No
9999	False	Caucasian	Male	[70-80)	?	Elective	Physician Referral	1	?	61	9	18	8	Yes

10000 rows × 14 columns

このデータセットでは、再入院の結果 (readmitted)、糖尿病の薬物治療の割付変数 (diabetesMed)、およびいくつかの特徴量があります。

可視化（オプション）

まずはじめに、薬物治療の割付変数と再入院の結果の関係（下図）を見てみます。

plot_df = working_df.groupby("diabetesMed").readmitted.mean().to_frame().reset_index()
p = sns.barplot(data=plot_df, x="diabetesMed", y="readmitted")
p.axes.yaxis.set_major_formatter(PercentFormatter(1))

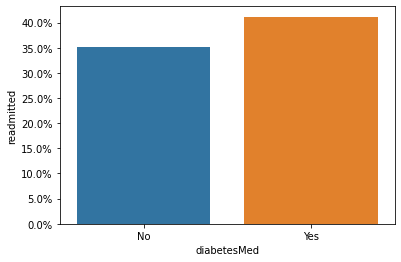
上記の結果を見ると、糖尿病の薬物治療を受けている患者はそうでない患者よりも再入院の確率がわずかに高く、あたかも薬物の治療が再入院のリスクを高めてしまっているように思われます。
以降のステップでは、この結果が正しい因果関係に基づくものなのか、あるいは見かけ上の相関関係に過ぎないのかを判断することを目的として分析を進めます。

Step2. 傾向スコアモデル (Propensity of Treatment model) のためのデータ準備

傾向スコアモデルとは、「効果を推定したい要因に割付られる確率 (これを傾向スコア (Propensity Score) という) 」 を予測するモデルのことです。

今回の例でいうと、治療の割付変数 (diabetesMed) をターゲットとし、本来のターゲット (readmitted) を除くすべての特徴量を用いて治療の割付確率を予測を行うモデルを作成します。

propensity_df = working_df.drop(columns=["readmitted"])
propensity_df

	race	gender	age	weight	admission_type_id	admission_source_id	number_inpatient	medical_specialty	num_lab_procedures	number_diagnoses	num_medications	time_in_hospital	diabetesMed
0	Caucasian	Female	[50-60)	?	Elective	Physician Referral	0	Surgery-Neuro	35	9	21	1	No
1	Caucasian	Female	[20-30)	[50-75)	Urgent	Physician Referral	0	?	8	6	5	2	No
2	Caucasian	Male	[80-90)	?	Not Available	NaN	1	Family/GeneralPractice	12	9	21	7	Yes
3	AfricanAmerican	Female	[50-60)	?	Emergency	Transfer from another health care facility	0	?	33	3	5	4	Yes
4	AfricanAmerican	Female	[50-60)	?	Emergency	Emergency Room	0	Psychiatry	31	7	13	5	Yes
...	...	...	...	...	...	...	...	...	...	...	...	...	...
9995	Caucasian	Female	[60-70)	?	Elective	Physician Referral	0	?	30	7	29	3	Yes
9996	AfricanAmerican	Male	[60-70)	?	Urgent	Emergency Room	0	Emergency/Trauma	1	9	15	8	Yes
9997	AfricanAmerican	Female	[70-80)	?	Emergency	Emergency Room	1	InternalMedicine	46	6	14	13	No
9998	Caucasian	Male	[80-90)	?	Urgent	Emergency Room	3	InternalMedicine	62	9	7	2	No
9999	Caucasian	Male	[70-80)	?	Elective	Physician Referral	1	?	61	9	18	8	Yes

10000 rows × 13 columns

治療群とコントロール群の比較

「なぜ、傾向スコアモデルを作る必要があるのか」を説明をする前に、今回の研究対象における治療群とコントロール群 (diabetesMed==Yes vs. diabetesMed==No) の特徴量の分布の違いを見てみることにしましょう。

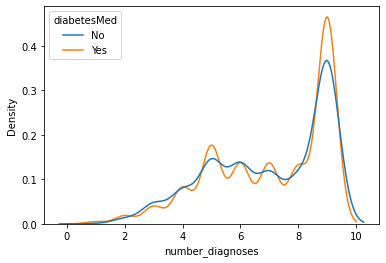
number_diagnoses ：診断件数

sns.kdeplot(
    data=propensity_df, x="number_diagnoses", hue="diabetesMed", common_norm=False
)

<AxesSubplot:xlabel='number_diagnoses', ylabel='Density'>

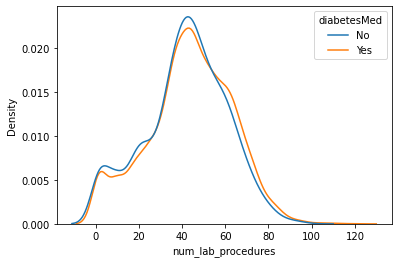
num_lab_procedures ：受診中に実施された臨床検査数

sns.kdeplot(
    data=propensity_df, x="num_lab_procedures", hue="diabetesMed", common_norm=False
)

<AxesSubplot:xlabel='num_lab_procedures', ylabel='Density'>

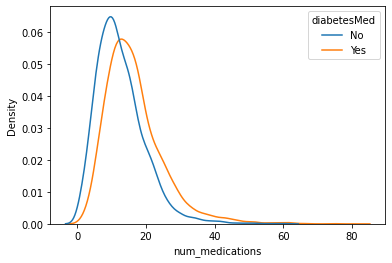
num_medications ：受診中に投与された薬品種数

sns.kdeplot(
    data=propensity_df, x="num_medications", hue="diabetesMed", common_norm=False
)

<AxesSubplot:xlabel='num_medications', ylabel='Density'>

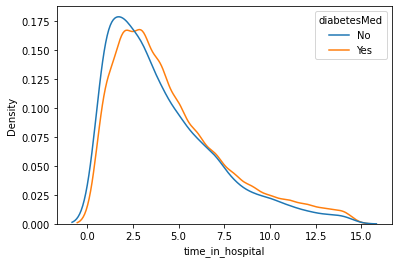
time_in_hospital ：入院から退院までの日数

sns.kdeplot(
    data=propensity_df, x="time_in_hospital", hue="diabetesMed", common_norm=False
)

<AxesSubplot:xlabel='time_in_hospital', ylabel='Density'>

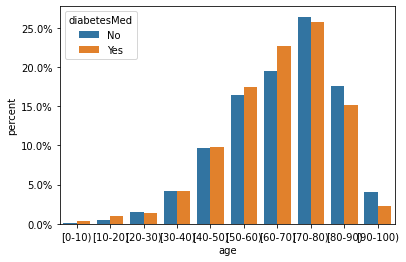
age ：年齢を10年間隔でグループ化

plot_df = (
    propensity_df.assign(sampling_weight=1)  # unweighted
    .groupby(["diabetesMed", "age"])
    .sampling_weight.sum()
    .pipe(lambda df: df / df.groupby("diabetesMed").transform("sum"))
    .to_frame("percent")
    .reset_index()
)
p = sns.barplot(data=plot_df, x="age", y="percent", hue="diabetesMed")
p.axes.yaxis.set_major_formatter(PercentFormatter(1))

注意
実際の分析では、残りのすべての特徴量についても同様の比較を行いましょう。

上記のプロットから、治療群とコントロール群は、特徴量num_medications、time_in_hospitalおよび ageについて異なる分布を持っていることがわかります。

交絡と傾向スコア

治療群とコントロール群の比較結果から、各被験者が治療を受けるかどうか (diabetesMed) はnum_medicationsやtime_in_hospital、ageなど様々な因子の影響を受けていることがわかりました。
また、こうした因子は治療の割付のみならず、研究の目的変数 (readmitted)自体にも影響を与えている可能性があります (下図)。

このような、研究の目的変数と割付変数の両方に影響を与え、その結果として因果関係を歪める可能性がある変数のことを交絡因子と呼び、今回の研究のように無作為割付を行っていない研究 (観測研究) ではこの交絡因子によるバイアスを排除することが課題の一つとなっています。

このような課題を解決するためのアイデアの一つが傾向スコアです。
傾向スコアを用いた分析手法はいくつか提案されており、本記事ではその詳細は割愛しますが、根本にあるアイデアは共通で、「治療群とコントロール群の間にある交絡因子の影響を調整すること」 です。

Step3. DataRobotによる傾向スコアモデルの構築

前ステップで用意したデータセットをもとに、各被験者の治療割付確率を予測するモデルをします。
DataRobotを使えば、多くの競合モデルを並行して探索し、最も良い結果を出すモデルを効率的に見つけ出すことができます。

補足
今回はPythonクライアントからモデルを作成しますが、DataRbootのGUI上でも同様のモデリング処理が実行可能です

プロジェクトの作成
先ほど作成したデータフレームからプロジェクトを作成します。

propensity_project = dr.Project.create(
    sourcedata=propensity_df, project_name="Propensity of Diabetes Medication"
)

構築するモデルの設定
次に、治療割付変数（diabetesMed）をターゲットとして、analyze_and_model()処理を開始します。

propensity_project.analyze_and_model(target="diabetesMed", worker_count=-1)

Project(Propensity of Diabetes Medication)

オートパイロットの実行
あとは、DataRobotのオートパイロットが完了するのを待ちます。

propensity_project.wait_for_autopilot(check_interval=30)

In progress: 4, queued: 0 (waited: 0s)
In progress: 4, queued: 0 (waited: 1s)
In progress: 4, queued: 0 (waited: 1s)
In progress: 4, queued: 0 (waited: 2s)
In progress: 3, queued: 0 (waited: 3s)
In progress: 2, queued: 0 (waited: 5s)
In progress: 1, queued: 0 (waited: 9s)
In progress: 1, queued: 0 (waited: 16s)
In progress: 1, queued: 0 (waited: 29s)
In progress: 1, queued: 0 (waited: 55s)
In progress: 16, queued: 0 (waited: 85s)
In progress: 4, queued: 0 (waited: 116s)
In progress: 0, queued: 0 (waited: 147s)
In progress: 0, queued: 0 (waited: 177s)
In progress: 1, queued: 0 (waited: 207s)
In progress: 1, queued: 0 (waited: 238s)
In progress: 0, queued: 0 (waited: 268s)
In progress: 0, queued: 0 (waited: 299s)
In progress: 0, queued: 0 (waited: 329s)

プロジェクトが完了したら、どのモデルが最も有効なモデルであるかを判断するために、プロジェクト内で作成されたモデルの評価指標、およびそれらに関するインサイトを確認していきます。

モデルと評価指標の確認
まず、リーダーボードで最もパフォーマンスの高いモデルを調べます。

propensity_model = propensity_project.get_top_model()
propensity_model

Model('Light Gradient Boosting on ElasticNet Predictions ')

今回のプロイジェクト内で作成したモデルの中で最も良いパフォーマンスを得られたモデルは Light Gradient Boosting on ElasticNet Predictions であることが確認できました。

評価指標もいくつか見てみましょう。

AUC

propensity_model.metrics.get("AUC")

{'validation': 0.68786,
 'crossValidation': 0.67601,
 'holdout': 0.66838,
 'training': None,
 'backtestingScores': None,
 'backtesting': None}

LogLoss

propensity_model.metrics.get("LogLoss")

{'validation': 0.52338,
 'crossValidation': 0.5273,
 'holdout': 0.53231,
 'training': None,
 'backtestingScores': None,
 'backtesting': None}

モデルのインサイトの確認

DataRobotでは、どの特徴量がターゲットの予測に影響を与えているのかについても確認することができます。
ここではその一例として、特徴量のインパクト (Feature Impact) を見てましょう。

def plot_feature_impact(datarobot_model, title=None, max_features=100):
    """This function plots feature impact
    Input:
        datarobot_model: <Datarobot Model object>
        title : <string> --> title of graph
    """
    # Get feature impact
    feature_impacts = datarobot_model.get_or_request_feature_impact()

    # Sort feature impact based on normalised impact
    feature_impacts.sort(key=lambda x: x["impactNormalized"], reverse=True)

    fi_df = pd.DataFrame(feature_impacts)  # Save feature impact in pandas dataframe
    fig, ax = plt.subplots(figsize=(14, 5))
    b = sns.barplot(
        y="featureName", x="impactNormalized", data=fi_df[:max_features], color="b"
    )
    b.axes.set_title("Feature Impact" if not title else title, fontsize=20)

plot_feature_impact(propensity_model)

特徴量のインパクトより、num_medications、time_in_hospital、ageなどの特徴量が、治療割付diabetesMedに影響を与えていることがわかります。
これは、Step2で見た結果と確かに一致しています。

注意
実際のプロジェクトでは、このモデルだけでなく、リーダーボードにあるの他のモデルについても深く掘り下げる必要があります。

Step4. 逆確率重み付き(Inverse Probability Weighting :IPW)による推定

今回紹介するコンテンツでは、傾向スコアを用いた代表的な手法の一つである、逆確率重み付き(Inverse Probability Weighting :IPW)による推定 を紹介しています。

IPWによる推定では、傾向スコアをサンプルの重みとして利用し、治療群とコントロール群のそれぞれの偏りを補正することでデータ全体での治療による効果を推定します。

傾向スコアの算出

はじめに、傾向スコアモデルから予測値 (傾向スコア) を取得します。
傾向スコアモデル作成時に使用したデータフレーム (diabetesMedを除く) を request_predictions() を用いてモデルに投入することで取得できます。

注意
本分析では、訓練データと同じデータを用いて予測を行っております。
今回のように、特定の研究集団における治療の傾向を分析するケースではこのようなアプローチをとることは可能ですが、標本外の集団を予測するようなケースでは注意が必要です。

scoring_df = propensity_df.drop(columns=["diabetesMed"])
scoring_df

	race	gender	age	weight	admission_type_id	admission_source_id	number_inpatient	medical_specialty	num_lab_procedures	number_diagnoses	num_medications	time_in_hospital
0	Caucasian	Female	[50-60)	?	Elective	Physician Referral	0	Surgery-Neuro	35	9	21	1
1	Caucasian	Female	[20-30)	[50-75)	Urgent	Physician Referral	0	?	8	6	5	2
2	Caucasian	Male	[80-90)	?	Not Available	NaN	1	Family/GeneralPractice	12	9	21	7
3	AfricanAmerican	Female	[50-60)	?	Emergency	Transfer from another health care facility	0	?	33	3	5	4
4	AfricanAmerican	Female	[50-60)	?	Emergency	Emergency Room	0	Psychiatry	31	7	13	5
...	...	...	...	...	...	...	...	...	...	...	...	...
9995	Caucasian	Female	[60-70)	?	Elective	Physician Referral	0	?	30	7	29	3
9996	AfricanAmerican	Male	[60-70)	?	Urgent	Emergency Room	0	Emergency/Trauma	1	9	15	8
9997	AfricanAmerican	Female	[70-80)	?	Emergency	Emergency Room	1	InternalMedicine	46	6	14	13
9998	Caucasian	Male	[80-90)	?	Urgent	Emergency Room	3	InternalMedicine	62	9	7	2
9999	Caucasian	Male	[70-80)	?	Elective	Physician Referral	1	?	61	9	18	8

10000 rows × 12 columns

predict_job = propensity_model.request_predictions(dataframe=scoring_df)
predict_job

PredictJob(Model('65a6eb2e6edd73b1994d580c'), status=queue)

propensity_predictions = predict_job.get_result_when_complete()
propensity_predictions

	row_id	prediction	positive_probability	prediction_threshold	class_No	class_Yes
0	0	Yes	0.812269	0.5	0.187731	0.812269
1	1	Yes	0.547232	0.5	0.452768	0.547232
2	2	Yes	0.889528	0.5	0.110472	0.889528
3	3	Yes	0.551166	0.5	0.448834	0.551166
4	4	Yes	0.769513	0.5	0.230487	0.769513
...	...	...	...	...	...	...
9995	9995	Yes	0.903911	0.5	0.096089	0.903911
9996	9996	Yes	0.832543	0.5	0.167457	0.832543
9997	9997	Yes	0.738654	0.5	0.261346	0.738654
9998	9998	Yes	0.709603	0.5	0.290397	0.709603
9999	9999	Yes	0.758729	0.5	0.241271	0.758729

10000 rows × 6 columns

propensity_scores_df = (
    propensity_predictions[["row_id", "class_Yes"]]
    .set_index("row_id")
    .rename(columns={"class_Yes": "propensity_score"})
)
propensity_scores_df

	propensity_score
row_id
0	0.812269
1	0.547232
2	0.889528
3	0.551166
4	0.769513
...	...
9995	0.903911
9996	0.832543
9997	0.738654
9998	0.709603
9999	0.758729

10000 rows × 1 columns

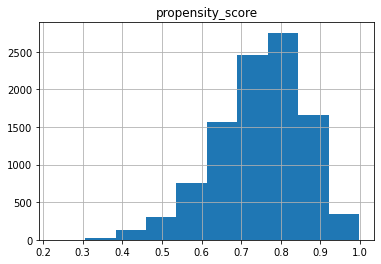
傾向スコアが得られました。
ヒストグラムで分布を見てみましょう。

propensity_scores_df.hist()

array([[<AxesSubplot:title={'center':'propensity_score'}>]], dtype=object)

逆確率の重みづけの計算
傾向スコアが得られたので、逆確率の重み付けを計算し、元のデータセット列に追加します。

def compute_iptw(df, stabilize=True):
    if stabilize:
        # Compute "stablized" weights to deal with extreme weight values
        numerator_treatment = (working_df.diabetesMed == "Yes").mean()
        numerator_control = (working_df.diabetesMed == "No").mean()
    else:
        # Use non-stablized weights
        numerator_treatment = 1
        numerator_control = 1
    return (df.diabetesMed == "Yes") * numerator_treatment / (df.propensity_score) + (
        df.diabetesMed == "No"
    ) * numerator_control / (1 - df.propensity_score)

iptw_df = (
    working_df.assign(
        row_id=lambda df: range(df.shape[0])
    )  # assign a 0 to (N-1) row ID, to match up with predictions
    .set_index("row_id")
    .join(propensity_scores_df, how="left")  # join propensity scores
    .assign(sampling_weight=compute_iptw)
)
iptw_df

	readmitted	race	gender	age	weight	admission_type_id	admission_source_id	number_inpatient	medical_specialty	num_lab_procedures	number_diagnoses	num_medications	time_in_hospital	diabetesMed	propensity_score	sampling_weight
row_id
0	False	Caucasian	Female	[50-60)	?	Elective	Physician Referral	0	Surgery-Neuro	35	9	21	1	No	0.812269	1.343415
1	False	Caucasian	Female	[20-30)	[50-75)	Urgent	Physician Referral	0	?	8	6	5	2	No	0.547232	0.557018
2	True	Caucasian	Male	[80-90)	?	Not Available	NaN	1	Family/GeneralPractice	12	9	21	7	Yes	0.889528	0.840671
3	False	AfricanAmerican	Female	[50-60)	?	Emergency	Transfer from another health care facility	0	?	33	3	5	4	Yes	0.551166	1.356761
4	False	AfricanAmerican	Female	[50-60)	?	Emergency	Emergency Room	0	Psychiatry	31	7	13	5	Yes	0.769513	0.971783
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
9995	False	Caucasian	Female	[60-70)	?	Elective	Physician Referral	0	?	30	7	29	3	Yes	0.903911	0.827293
9996	False	AfricanAmerican	Male	[60-70)	?	Urgent	Emergency Room	0	Emergency/Trauma	1	9	15	8	Yes	0.832543	0.898212
9997	True	AfricanAmerican	Female	[70-80)	?	Emergency	Emergency Room	1	InternalMedicine	46	6	14	13	No	0.738654	0.965004
9998	False	Caucasian	Male	[80-90)	?	Urgent	Emergency Room	3	InternalMedicine	62	9	7	2	No	0.709603	0.868465
9999	False	Caucasian	Male	[70-80)	?	Elective	Physician Referral	1	?	61	9	18	8	Yes	0.758729	0.985596

10000 rows × 16 columns

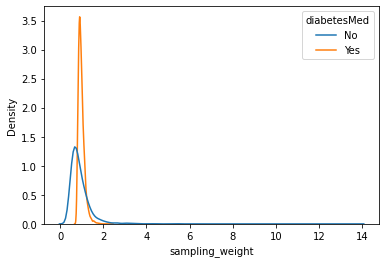
sns.kdeplot(data=iptw_df, x="sampling_weight", hue="diabetesMed", common_norm=False)

<AxesSubplot:xlabel='sampling_weight', ylabel='Density'>

Step5. IPWを用いた因果関係の評価

IPWによる補正を行うことで、元のデータセット全体と類似した特徴量の分布を持つ治療群とコントロール群を作成することができます。
これにより因果関係を決定するための比較を行うことが可能になります。

IPW調整後の治療群とコントロール群の比較

Step2で異なる分布を持つことを確認した特徴量について、IPWの調整によって分布がどのように補正されたかを見ていきましょう。

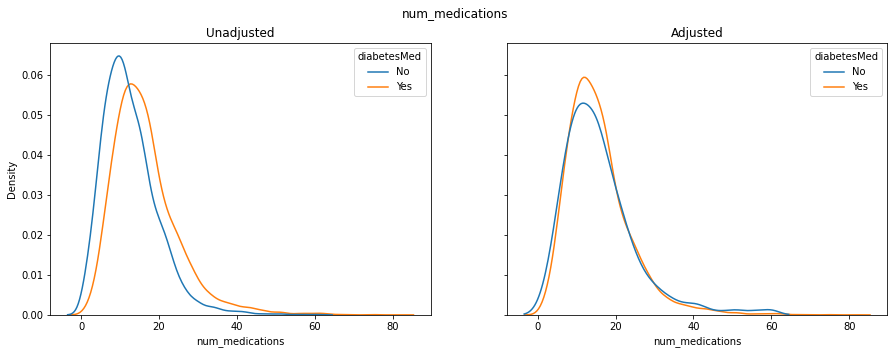
num_medications ：受診中に投与された薬品種数

fig, axes = plt.subplots(1, 2, figsize=(15, 5), sharey=True)
fig.suptitle("num_medications")
axes[0].set_title("Unadjusted")
axes[1].set_title("Adjusted")
sns.kdeplot(
    data=propensity_df,
    x="num_medications",
    hue="diabetesMed",
    common_norm=False,
    ax=axes[0],
)
sns.kdeplot(
    data=iptw_df,
    x="num_medications",
    hue="diabetesMed",
    common_norm=False,
    ax=axes[1],
    weights="sampling_weight",
)
None

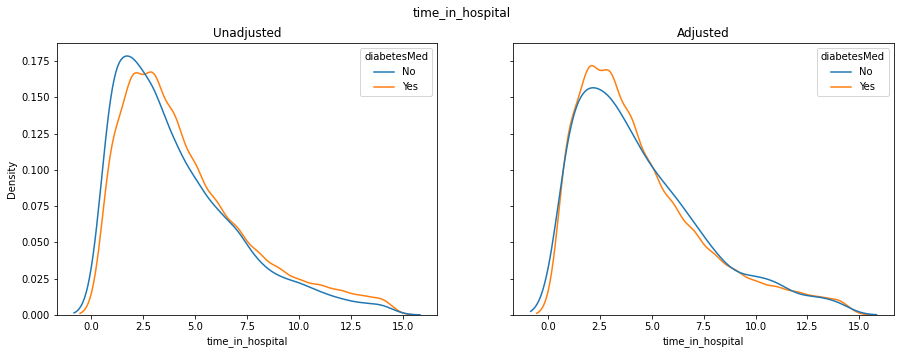
time_in_hospital ：入院から退院までの日数

fig, axes = plt.subplots(1, 2, figsize=(15, 5), sharey=True)
fig.suptitle("time_in_hospital")
axes[0].set_title("Unadjusted")
axes[1].set_title("Adjusted")
sns.kdeplot(
    data=propensity_df,
    x="time_in_hospital",
    hue="diabetesMed",
    common_norm=False,
    ax=axes[0],
)
sns.kdeplot(
    data=iptw_df,
    x="time_in_hospital",
    hue="diabetesMed",
    common_norm=False,
    ax=axes[1],
    weights="sampling_weight",
)
None

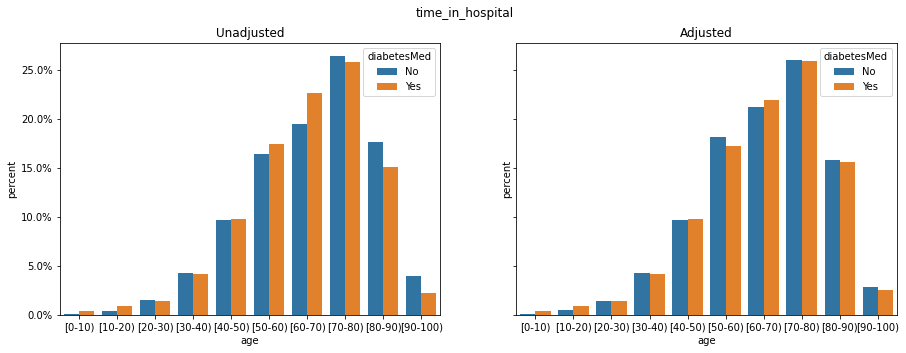
age ：年齢を10年間隔でグループ化

PERCENT_FORMAT_STRING_0_100 = (
    "{x:.1f}%"  # format string for formatting 0-100 floats as a percentage
)


def prepare_categorical_plot_df(categorical_var, weight=True):
    if not weight:
        plot_df = iptw_df.assign(sampling_weight=1)  # unweighted
    else:
        plot_df = iptw_df

    plot_df = (
        plot_df.groupby(["diabetesMed", categorical_var])
        .sampling_weight.sum()
        .pipe(
            lambda df: 100 * (df / df.groupby("diabetesMed").transform("sum"))
        )  # we are using 0-100 values for percentage (for compatibility with bar labels)
        .to_frame("percent")
        .reset_index()
    )

    return plot_df

fig, axes = plt.subplots(1, 2, figsize=(15, 5), sharey=True)
fig.suptitle("time_in_hospital")
axes[0].set_title("Unadjusted")
axes[1].set_title("Adjusted")
sns.barplot(
    data=prepare_categorical_plot_df("age", weight=False),
    x="age",
    y="percent",
    hue="diabetesMed",
    ax=axes[0],
)
sns.barplot(
    data=prepare_categorical_plot_df("age", weight=True),
    x="age",
    y="percent",
    hue="diabetesMed",
    ax=axes[1],
)
axes[0].yaxis.set_major_formatter(PERCENT_FORMAT_STRING_0_100)
None

プロットを見た結果、調整された治療群とコントロール群の分布が類似してることがわかります。
この調整は元のデータセット全体の分布に近づくように行われています。

注意
実際の分析では、残りのすべての特徴量についても同様の比較を行いましょう。

以上の結果から、IPWによる補正により治療群とコントロール群を"現在観測できている因子に限って"元のデータセット全体と同じような分布を持つ集団とみなした比較をすることができるようになりました。

Step6. 調整された治療効果の確認

IPWを用いることで、交絡の影響を取り除いた比較ができるようになりました。
改めて、治療割付群とコントロール群のアウトカムの比較、すなわち再入院確率の比較をしてみましょう。

fig, axes = plt.subplots(1, 2, figsize=(15, 5), sharey=True)
fig.suptitle("readmitted")
axes[0].set_title("Unadjusted")
axes[1].set_title("Adjusted")
sns.barplot(
    data=prepare_categorical_plot_df("readmitted", weight=False).pipe(
        lambda df: df[df.readmitted == True]
    ),
    x="diabetesMed",
    y="percent",
    ax=axes[0],
)
sns.barplot(
    data=prepare_categorical_plot_df("readmitted", weight=True).pipe(
        lambda df: df[df.readmitted == True]
    ),
    x="diabetesMed",
    y="percent",
    ax=axes[1],
)
axes[0].yaxis.set_major_formatter(PERCENT_FORMAT_STRING_0_100)
for ax in axes:
    for container in ax.containers:
        ax.bar_label(container, fmt="%.1f%%")
None

・・・あまり変わっていないですね！
観察された交絡因子で調整した後でも、糖尿病治療を受けている患者の再入院率の方が高いです。

この結果から以下の可能性が考えられます：

1. 糖尿病薬物療法は本当に糖尿病入院患者の再入院リスクを増加させている。
   こう結論付けてよいかどうかは、先行知見との整合性や妥当性などの観点から検討する必要がありそうです。

2. 因果関係について未観測の交絡因子があり、それが傾向スコアモデルに反映されていない。
   Step5の終わりに記載した通り、今回の分析による補正は"現在観測できている因子に限って"行われたものであり、未観測の因子の影響については考慮されていません。
   例えば、今回のデータセットの中には「重症度」や「入院理由」など、割付変数と結果変数の双方に影響を与える可能性が高い因子に関連する情報を含んでいません。
   こうした重要な因子を観測できていないことで、十分な補正ができていなかった可能性があります。

3. 糖尿病の薬物投与が「一貫性のある」指標ではない
   統計的因果推論の中の重要な仮定の一つである一貫性: Consistencyに違反している可能性があります。
   Consistencyに関する詳細な説明は割愛しますが、今回の例でいうと以下のような可能性が考えられます。
   一言に「薬品の投与」といっても、量・時間・回数・方法など様々なパターンがあります。そもそも薬品の種類自体が被験者によって違う可能性もあるかもしれません。
   これらの条件が厳密に定義されていない場合、「薬品の投与」による効果を評価することはできません。

まとめ

今回は、観察データを用いた分析の中で問題となる交絡への対処方法について、傾向スコアの逆確率重み付け推定を用いた効果測定の方法をご紹介しました。
このアプローチは観測研究の分析のみならず、ビジネス上での課題にも適用可能であり、ビジネスにおいて行われたアクションがKPIに与えた影響を正しく比較する場合にも有効な手法です。

当部のデータサイエンティストは、DataRobot によるモデリングのみでなく、その結果を適切に解釈し、データドリブンな意思決定を正しく行うための支援も行っております。

仲間募集

NTTデータ テクノロジーコンサルティング事業本部 では、以下の職種を募集しています。

1. クラウド技術を活用したデータ分析プラットフォームの開発・構築(ITアーキテクト/クラウドエンジニア)

クラウド／プラットフォーム技術の知見に基づき、DWH、BI、ETL領域におけるソリューション開発を推進します。
https://enterprise-aiiot.nttdata.com/recruitment/career_sp/cloud_engineer

2. データサイエンス領域（データサイエンティスト／データアナリスト）

データ活用／情報処理／AI／BI／統計学などの情報科学を活用し、よりデータサイエンスの観点から、データ分析プロジェクトのリーダーとしてお客様のDX／デジタルサクセスを推進します。
https://enterprise-aiiot.nttdata.com/recruitment/career_sp/datascientist

3.お客様のAI活用の成功を推進するAIサクセスマネージャー

DataRobotをはじめとしたAIソリューションやサービスを使って、
お客様のAIプロジェクトを成功させ、ビジネス価値を創出するための活動を実施し、
お客様内でのAI活用を拡大、NTTデータが提供するAIソリューションの利用継続を推進していただく人材を募集しています。
https://nttdata.jposting.net/u/job.phtml?job_code=804

4.DX／デジタルサクセスを推進するデータサイエンティスト《管理職/管理職候補》

データ分析プロジェクトのリーダとして、正確な課題の把握、適切な評価指標の設定、分析計画策定や適切な分析手法や技術の評価・選定といったデータ活用の具現化、高度化を行い分析結果の見える化・お客様の納得感醸成を行うことで、ビジネス成果・価値を出すアクションへとつなげることができるデータサイエンティスト人材を募集しています。

https://nttdata.jposting.net/u/job.phtml?job_code=898

ソリューション紹介

Trusted Data Foundationについて

～データ資産を分析活用するための環境をオールインワンで提供するソリューション～
https://enterprise-aiiot.nttdata.com/tdf/
最新のクラウド技術を採用して弊社が独自に設計したリファレンスアーキテクチャ（Datalake+DWH+AI/BI）を顧客要件に合わせてカスタマイズして提供します。
可視化、機械学習、DeepLearningなどデータ資産を分析活用するための環境がオールインワンで用意されており、これまでとは別次元の量と質のデータを用いてアジリティ高くDX推進を実現できます。

TDFⓇ-AM（Trusted Data Foundation - Analytics Managed Service）について

～データ活用基盤の段階的な拡張支援（Quick Start) と保守運用のマネジメント（Analytics Managed）をご提供することでお客様のDXを成功に導く、データ活用プラットフォームサービス～
https://enterprise-aiiot.nttdata.com/service/tdf/tdf_am
TDFⓇ-AMは、データ活用をQuickに始めることができ、データ活用の成熟度に応じて段階的に環境を拡張します。プラットフォームの保守運用はNTTデータが一括で実施し、お客様は成果創出に専念することが可能です。また、日々最新のテクノロジーをキャッチアップし、常に活用しやすい環境を提供します。なお、ご要望に応じて上流のコンサルティングフェーズからAI/BIなどのデータ活用支援に至るまで、End to Endで課題解決に向けて伴走することも可能です。

NTTデータとTableauについて

ビジュアル分析プラットフォームのTableauと2014年にパートナー契約を締結し、自社の経営ダッシュボード基盤への採用や独自のコンピテンシーセンターの設置などの取り組みを進めてきました。さらに2019年度にはSalesforceとワンストップでのサービスを提供開始するなど、積極的にビジネスを展開しています。

これまでPartner of the Year, Japanを4年連続で受賞しており、2021年にはアジア太平洋地域で最もビジネスに貢献したパートナーとして表彰されました。
また、2020年度からは、Tableauを活用したデータ活用促進のコンサルティングや導入サービスの他、AI活用やデータマネジメント整備など、お客さまの企業全体のデータ活用民主化を成功させるためのノウハウ・方法論を体系化した「デジタルサクセス」プログラムを提供開始しています。
https://enterprise-aiiot.nttdata.com/service/tableau

NTTデータとAlteryxについて

Alteryxは、業務ユーザーからIT部門まで誰でも使えるセルフサービス分析プラットフォームです。

Alteryx導入の豊富な実績を持つNTTデータは、最高位にあたるAlteryx Premiumパートナーとしてお客さまをご支援します。

導入時のプロフェッショナル支援など独自メニューを整備し、特定の業種によらない多くのお客さまに、Alteryxを活用したサービスの強化・拡充を提供します。

https://enterprise-aiiot.nttdata.com/service/alteryx

NTTデータとDataRobotについて

DataRobotは、包括的なAIライフサイクルプラットフォームです。

NTTデータはDataRobot社と戦略的資本業務提携を行い、経験豊富なデータサイエンティストがAI・データ活用を起点にお客様のビジネスにおける価値創出をご支援します。

https://enterprise-aiiot.nttdata.com/service/datarobot

NTTデータとInformaticaについて

データ連携や処理方式を専門領域として10年以上取り組んできたプロ集団であるNTTデータは、データマネジメント領域でグローバルでの高い評価を得ているInformatica社とパートナーシップを結び、サービス強化を推進しています。
https://enterprise-aiiot.nttdata.com/service/informatica

NTTデータとSnowflakeについて

NTTデータでは、Snowflake Inc.とソリューションパートナー契約を締結し、クラウド・データプラットフォーム「Snowflake」の導入・構築、および活用支援を開始しています。

NTTデータではこれまでも、独自ノウハウに基づき、ビッグデータ・AIなど領域に係る市場競争力のあるさまざまなソリューションパートナーとともにエコシステムを形成し、お客さまのビジネス変革を導いてきました。
Snowflakeは、これら先端テクノロジーとのエコシステムの形成に強みがあり、NTTデータはこれらを組み合わせることでお客さまに最適なインテグレーションをご提供いたします。

https://enterprise-aiiot.nttdata.com/service/snowflake