Unity における CPU ベースの揺れ物の実装について調査しました。
今回は特に以下の点を中心に検証しました。
- ポータブルな SIMD 対応
- マルチスレッド実行
揺れ物のアルゴリズムについて
\ x_{n+1} = \vec{2X_{n}} - \vec{X_{n-1}} + \vec{A}(\vec{X_n})Δt^2 \
検証ではベルレ積分による位置ベース物理を採用しました。
記事トップの動画像では髪の毛のジョイントに対してシミュレーションを実行しています。
位置ベースの物理は計算が単純で低負荷であり、挙動も安定しています。
これはパフォーマンス要件が厳しいゲーム開発においてメリットが多いと感じます。
また、当該アルゴリズムはシミュレーション対象の位置を直接変更できる性質があります。
これにより衝突の解決や拘束の実装などが簡単に行えます。
位置ベースの物理の仕組みについては、以下のリンクが分かりやすいかと思います。
SIMD対応
Unity の mathematics を利用しました。
通常 SIMD は CPU に応じて命令が異なりますが、mathematics は数学に特化して
命令をラップしたものです。
これを使用することで CPU に依存しないポータブルな実装が可能になります。
例えば検証では mathematics に含まれる float3 を Vector3 として利用せず、
float4 を3つ並べた以下のような SVector3 を実装しました。
[BurstCompile]
public struct SVector3
{
public float4 x;
public float4 y;
public float4 z;
private static readonly SVector3 _zeroVector = new SVector3(Vector3.zero);
public static SVector3 ZeroVector => _zeroVector;
private static readonly SVector3 _oneVector = new SVector3(Vector3.one);
public static SVector3 OneVector => _oneVector;
private static readonly SVector3 _upVector = new SVector3(SMathConstans.ZeroReal, SMathConstans.OneReal, SMathConstans.ZeroReal);
public static SVector3 UpVector => _upVector;
private static readonly SVector3 _rightVector = new SVector3(SMathConstans.OneReal, SMathConstans.ZeroReal, SMathConstans.ZeroReal);
public static SVector3 RightVector => _rightVector;
private static readonly SVector3 _forwardVector = new SVector3(SMathConstans.ZeroReal, SMathConstans.ZeroReal, SMathConstans.OneReal);
public static SVector3 ForwardVector => _forwardVector;
private static readonly SVector3 _yAxisVector = new SVector3(SMathConstans.ZeroReal, SMathConstans.OneReal, SMathConstans.ZeroReal);
public static SVector3 YAxisVector => _yAxisVector;
private static readonly SVector3 _xAxisVector = new SVector3(SMathConstans.OneReal, SMathConstans.ZeroReal, SMathConstans.ZeroReal);
public static SVector3 XAxisVector => _xAxisVector;
private static readonly SVector3 _zAxisVector = new SVector3(SMathConstans.ZeroReal, SMathConstans.ZeroReal, SMathConstans.OneReal);
public static SVector3 ZAxisVector => _zAxisVector;
[MethodImpl(MethodImplOptions.AggressiveInlining)]
public SVector3(Vector3 x, Vector3 y, Vector3 z, Vector3 w)
{
this.x = new float4(x.x, y.x, z.x, w.x);
this.y = new float4(x.y, y.y, z.y, w.y);
this.z = new float4(x.z, y.z, z.z, w.z);
}
[MethodImpl(MethodImplOptions.AggressiveInlining)]
public SVector3(Vector3 v)
: this(v, v, v, v)
{
}
[MethodImpl(MethodImplOptions.AggressiveInlining)]
public SVector3(float4 x, float4 y, float4 z)
{
this.x = x;
this.y = y;
this.z = z;
}
[MethodImpl(MethodImplOptions.AggressiveInlining)]
public static SVector3 operator +(SVector3 lhs, SVector3 rhs)
{
return new SVector3(lhs.x + rhs.x, lhs.y + rhs.y, lhs.z + rhs.z);
}
[MethodImpl(MethodImplOptions.AggressiveInlining)]
public static SVector3 operator -(SVector3 lhs, SVector3 rhs)
{
return new SVector3(lhs.x - rhs.x, lhs.y - rhs.y, lhs.z - rhs.z);
}
[MethodImpl(MethodImplOptions.AggressiveInlining)]
public static SVector3 operator -(SVector3 a)
{
return new SVector3(-a.x, -a.y, -a.z);
}
[MethodImpl(MethodImplOptions.AggressiveInlining)]
public static SVector3 operator *(float4 lhs, SVector3 rhs)
{
return new SVector3(lhs * rhs.x, lhs * rhs.y, lhs * rhs.z);
}
[MethodImpl(MethodImplOptions.AggressiveInlining)]
public static SVector3 operator *(SVector3 lhs, float4 rhs)
{
return new SVector3(rhs * lhs.x, rhs * lhs.y, rhs * lhs.z);
}
[MethodImpl(MethodImplOptions.AggressiveInlining)]
public static SVector3 operator *(SVector3 lhs, SVector3 rhs)
{
return new SVector3(lhs.x * rhs.x, lhs.y * rhs.y, lhs.z * rhs.z);
}
[MethodImpl(MethodImplOptions.AggressiveInlining)]
public static SVector3 operator /(SVector3 lhs, float4 rhs)
{
return new SVector3(lhs.x / rhs, lhs.y / rhs, lhs.z / rhs);
}
public Vector3 this[int index]
{
get
{
return new Vector3(x[index], y[index], z[index]);
}
set
{
x[index] = value.x;
y[index] = value.y;
z[index] = value.z;
}
}
public readonly void Break(Span<Vector3> Vectors)
{
Vectors[0] = new Vector3(x.x, y.x, z.x);
Vectors[1] = new Vector3(x.y, y.y, z.y);
Vectors[2] = new Vector3(x.z, y.z, z.z);
Vectors[3] = new Vector3(x.w, y.w, z.w);
}
public readonly void Break(out Vector3 v0, out Vector3 v1, out Vector3 v2, out Vector3 v3)
{
v0 = new Vector3(x.x, y.x, z.x);
v1 = new Vector3(x.y, y.y, z.y);
v2 = new Vector3(x.z, y.z, z.z);
v3 = new Vector3(x.w, y.w, z.w);
}
[MethodImpl(MethodImplOptions.AggressiveInlining)]
public static float4 Dot(SVector3 lhs, SVector3 rhs)
{
return lhs.x * rhs.x + lhs.y * rhs.y + lhs.z * rhs.z;
}
[MethodImpl(MethodImplOptions.AggressiveInlining)]
public static SVector3 Cross(SVector3 lhs, SVector3 rhs)
{
return new SVector3(lhs.y * rhs.z - lhs.z * rhs.y, lhs.z * rhs.x - lhs.x * rhs.z, lhs.x * rhs.y - lhs.y * rhs.x);
}
[MethodImpl(MethodImplOptions.AggressiveInlining)]
public static float4 Distance(SVector3 lhs, SVector3 rhs)
{
float4 x = lhs.x - rhs.x;
float4 y = lhs.y - rhs.y;
float4 z = lhs.z - rhs.z;
return math.sqrt(x * x + y * y + z * z);
}
[MethodImpl(MethodImplOptions.AggressiveInlining)]
public static float4 Magnitude(SVector3 v)
{
return math.sqrt((v.x * v.x) + (v.y * v.y) + (v.z * v.z));
}
[MethodImpl(MethodImplOptions.AggressiveInlining)]
public static float4 SqrMagnitude(SVector3 v)
{
return (v.x * v.x) + (v.y * v.y) + (v.z * v.z);
}
[MethodImpl(MethodImplOptions.AggressiveInlining)]
public static SVector3 Normalize(SVector3 v)
{
float4 lenght = Magnitude(v);
bool4 safeMask = lenght > SMathConstans.SmallReal;
float4 safeLength = SMathLibrary.Select(safeMask, lenght, SMathConstans.OneReal);
return SMathLibrary.Select(lenght > SMathConstans.SmallReal, v / safeLength, SVector3.ZeroVector);
}
[MethodImpl(MethodImplOptions.AggressiveInlining)]
public static SVector3 GetSafeScaleReciprocalt(SVector3 scale)
{
SVector3 SafeReciprocalScale = SVector3.ZeroVector;
SafeReciprocalScale.x = SMathLibrary.Select(math.abs(scale.x) > SMathConstans.SmallReal, SMathConstans.OneReal / scale.x, SMathConstans.ZeroReal);
SafeReciprocalScale.y = SMathLibrary.Select(math.abs(scale.y) > SMathConstans.SmallReal, SMathConstans.OneReal / scale.y, SMathConstans.ZeroReal);
SafeReciprocalScale.z = SMathLibrary.Select(math.abs(scale.z) > SMathConstans.SmallReal, SMathConstans.OneReal / scale.z, SMathConstans.ZeroReal);
return SafeReciprocalScale;
}
};
float4 を利用することで多くのケースで SIMD のレジスタを余すことがなくなり、
4つの3次元ベクトルが並列に処理されます。
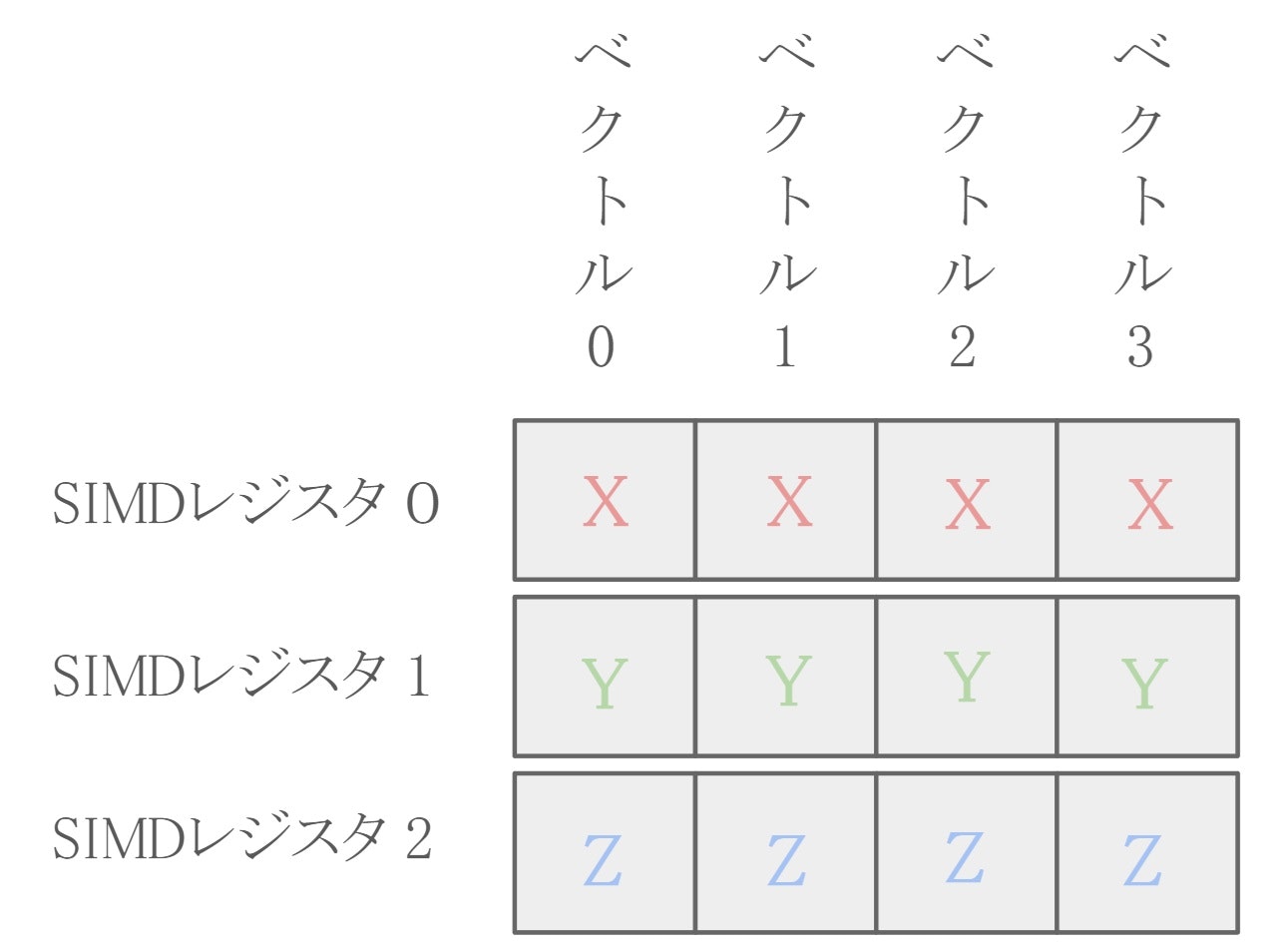
またベクトルクラスの実装においてはインターフェースをVector3 に寄せることで、SVector3 が内部に持つ4つの Vector3 を意識することなく、直観的に操作できるようになっています。
使用例として、外力を加えるコードは以下のようになっています。
public static void AddForces(ref DynamicBoneSolver solver, in SimulationContext simulationContext)
{
float4 deltaTimeFactor = simulationContext.DeltaTime * simulationContext.BaseFrameRate;
// 重力
SVector3 gravity = SVector3.UpVector * new float4(9.18f * simulationContext.DeltaTime * simulationContext.DeltaTime);
for (int packedPositionIndex = 0; packedPositionIndex < solver.SimPositions.Length; ++packedPositionIndex)
{
solver.SimPositions[packedPositionIndex] -= gravity * solver.FixedMasks[packedPositionIndex];
}
// 姿勢変化に伴う外力
SVector3 worldVelocity = STransform.InverseTransformPosition(simulationContext.OwnerTransform, simulationContext.PrevOwnerTransform.Translation);
SQuaternion worldAngularVelocity = STransform.InverseTransformRotation(simulationContext.OwnerTransform, simulationContext.PrevOwnerTransform.Rotation);
for (int packedPositionIndex = 0; packedPositionIndex < solver.SimPositions.Length; ++packedPositionIndex)
{
SVector3 prevSimPosition = solver.PrevSimPositions[packedPositionIndex];
SVector3 linearizedWorldAngularVelocity = SQuaternion.RotateVector(worldAngularVelocity, prevSimPosition) - prevSimPosition;
solver.SimPositions[packedPositionIndex] += (worldVelocity + linearizedWorldAngularVelocity) * solver.FixedMasks[packedPositionIndex] * deltaTimeFactor;
}
}
SVector3 と同じ思想で Quaternion や Trnasform も SIMD対応しています。
SIMD については以下が参考になります。
マルチスレッド実行
Unity の Animation C# Jobs を利用しました。
ジョブについては以下のようなコードになります。
[BurstCompile]
public struct FuwaFuwaJob : IAnimationJob
{
public float DeltaTime;
public DynamicBoneSolver Solver;
public SimulationContext SimulationContext;
public PhysicsSettings PhysicsSettings;
public void ProcessAnimation(AnimationStream stream)
{
SolverLibrary.UpdateSimulationContext(in Solver, ref SimulationContext, stream);
SolverLibrary.UpdateAnimationPose(ref Solver, stream);
SolverLibrary.UpdateFixedPositions(ref Solver, stream);
if (SimulationContext.IsFirstUpdate)
{
PhysicsLibrary.ResetSimulationPose(ref Solver);
PhysicsLibrary.ResetVelocity(ref Solver);
SimulationContext.IsFirstUpdate = false;
}
// 重力、キャラクターの姿勢変化による外力を加える
PhysicsLibrary.AddForces(ref Solver, in SimulationContext);
// ベルレ積分
PhysicsLibrary.VerletIntegrate(ref Solver, in SimulationContext);
// 構造を維持するための拘束を実行
ConstraintLibrary.ResetLambdas(ref Solver);
for (int i = 0; i < PhysicsSettings.SolverIterations; ++i)
{
ConstraintLibrary.ConstraintVerticalStructure(ref Solver, ref SimulationContext, ref PhysicsSettings);
}
// シミュレーション結果をアニメーションポーズとして出力
SolverLibrary.ApplySimulationResult(in Solver, stream);
}
public void ProcessRootMotion(AnimationStream stream)
{
}
};
IAnimationJob.ProcessAnimation() にてシミュレーションを実行しています。
当該関数はアニメーションジョブとして毎フレーム呼び出されます。
ジョブの登録については以下のようなコードになります。
// 揺れ物の計算を行うジョブの作成
FuwaFuwaJob job = new FuwaFuwaJob
{
Solver = _solver,
SimulationContext = new SimulationContext { IsFirstUpdate = true, BaseFrameRate = 60 },
PhysicsSettings = _physicsSettings,
};
// ジョブはPlayable APIで実行します
// グラフの作成
_graph = PlayableGraph.Create("FuwaFuwa Job");
_graph.SetTimeUpdateMode(DirectorUpdateMode.GameTime);
// ジョブを実行するノードを生成
AnimationScriptPlayable scriptPlayable = AnimationScriptPlayable.Create(_graph, job, 1);
// アニメーションクリップのノードを接続
// これはアニメーション結果に対して物理効果を乗せるため
if (_animClip != null)
{
AnimationClipPlayable animClipPlayable = AnimationClipPlayable.Create(_graph, _animClip);
_graph.Connect(animClipPlayable, 0, scriptPlayable, 0);
}
AnimationPlayableOutput playableOutput = AnimationPlayableOutput.Create(_graph, "Animation Output", animator);
playableOutput.SetSourcePlayable(scriptPlayable);
_graph.Play();
基本的にやることは AnimationScriptPlayable にジョブを設定するだけです。
詳細については以下のようなリンクが参考になるかと思います。
- 【Unity】Animation C# Jobsで遊んでみる
- 【Unity】アニメーション制御に色々と良さそうな"Playable API"について云々
- Unityアニメーションシステムの 今と未来の話
検証したソースコード
上記にて公開しています。
FuwaFuwa/Runtime/Scritps/FuwaFuwaComponent.cs をアタッチして、
RootBone に揺れ物の根元のジョイントを指定して利用することを想定しています。
調整用の減衰パラメータがハードコーディングになっている等、
あくまでも検証用のコードであることに注意してください。
数学ライブラリについては /FuwaFuwa/SMath/Runtime/Scripts/ 以下にまとまっています。
所感
Unity の mathematics と Animation C# Jobs を利用することで、
SIMD と マルチスレッドに対応した揺れ物を実装できそうなことが分かりました。
SIMD の対応において4つの座標をまとめて扱うコードを書きました。
SIMD のレジスタを意識して、後から高速化のために変更を行うのは
骨が折れると思われます。
そのため SIMD の利用を検討する場合は、実装の初期からデータ構造とアルゴリズムを
SIMDに合わせて設計したほうが良さそうです。

