量子分類器
量子回路にパラメータを埋めておいて、機械学習として最適化することで望む非線形モデルを構築できます。
今回は分類器を作ってみます。
データセットはirisを使い、SDKとしては量子部分はPennyLane、古典部分はTensorflow(及びKeras)を用います。
コード
import
使わないものもありますが、
from keras.models import Sequential
from keras.layers.core import Dense, Activation
import pennylane as qml
from pennylane import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import pandas as pd
from sklearn import datasets
from keras import initializers
from keras import optimizers
from keras.callbacks import EarlyStopping
データ準備
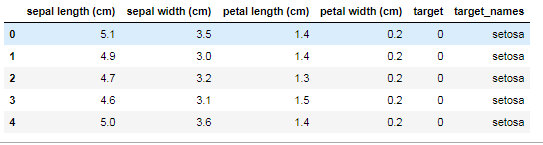
# Irisデータセットの読み込み
iris = datasets.load_iris()
# 扱いやすいよう、pandasのDataFrame形式に変換
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df['target'] = iris.target
df['target_names'] = iris.target_names[iris.target]
df.head()
## 教師データ作成
# ここではpetal length, petal widthの2種類のデータを用いる。より高次元への拡張は容易である。
x_train = df.loc[:,['petal length (cm)', 'petal width (cm)']].to_numpy() # shape:(150, 2)
y_train = np.eye(3)[iris.target] # one-hot 表現 shape:(150, 3)
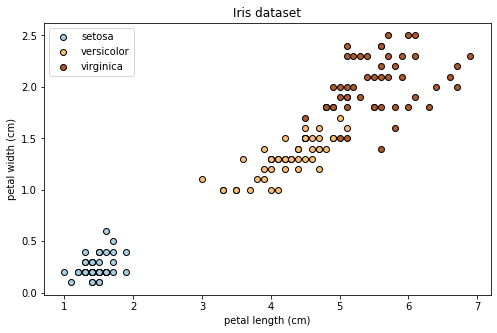
# データ点のプロット
plt.figure(figsize=(8, 5))
for t in range(3):
x = x_train[iris.target==t][:,0]
y = x_train[iris.target==t][:,1]
cm = [plt.cm.Paired([c]) for c in [0,6,11]]
plt.scatter(x, y, c=cm[t], edgecolors='k', label=iris.target_names[t])
# label
plt.title('Iris dataset')
plt.xlabel('petal length (cm)')
plt.ylabel('petal width (cm)')
plt.legend()
plt.show()
学習
古典 Neural Network
まずは古典NNをやってみます。
param = {'num_hidden_layers': 2, 'num_nodes': 20, 'num_epochs':128, 'activation': 'relu'}
# multilayer perceptron
model = Sequential()
for _ in range(param['num_hidden_layers']):
model.add(Dense(param['num_nodes'], input_dim=2,use_bias='False'))
model.add(Activation(param['activation']))
model.add(Dense(3))
model.add(Activation('softmax'))
Adamopt = optimizers.Adam(lr=0.01)
model.compile(loss='categorical_crossentropy', optimizer=Adamopt)
early_stopping = EarlyStopping(patience=10, verbose=0)
hist = model.fit(x_train, y_train, validation_split=0.1, epochs=param['num_epochs'], verbose=0, shuffle='True', batch_size=30, callbacks=[early_stopping])
loss = hist.history['loss']
val_loss = hist.history['val_loss']
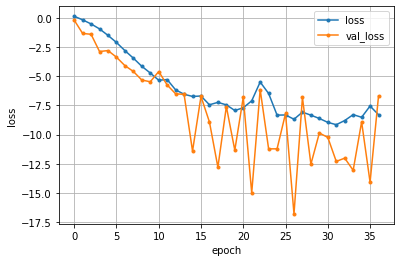
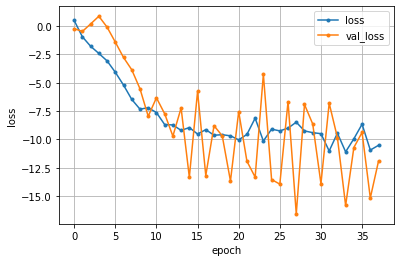
# lossのグラフ
plt.plot(range(len(loss)), 10*np.log10(loss), marker='.', label='loss')
plt.plot(range(len(val_loss)), 10*np.log10(val_loss), marker='.', label='val_loss')
plt.legend(loc='best', fontsize=10)
plt.grid()
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()
数秒で終わります。
Epoch 1/128 5/5 [==============================] - 1s 49ms/step - loss: 1.0702 - val_loss: 0.9317 Epoch 2/128 5/5 [==============================] - 0s 14ms/step - loss: 0.9300 - val_loss: 0.6034 Epoch 3/128 5/5 [==============================] - 0s 12ms/step - loss: 0.8668 - val_loss: 0.7717
1epochは0.1秒以下で終わっているようです。
予測してみます。(予測といいつつ、教師データを使いまわしています。動作確認だけなのでご容赦)
Pred = model.predict_classes(x_train)
import matplotlib.cm as cm
colors = cm.rainbow(np.linspace(0, 1, 3))
# 描画サイズ
plt.figure(figsize=(8, 6))
# 説明変数の散布図
for i in range(3):
plt.scatter(x_train[Pred==i, 0], x_train[Pred==i, 1], color=colors[i], edgecolor='white', s=70)
# ラベルとタイトル
plt.xlabel('data1')
plt.ylabel('data2')
# 描画
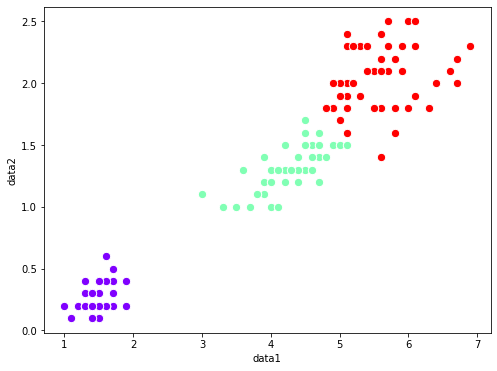
plt.show()
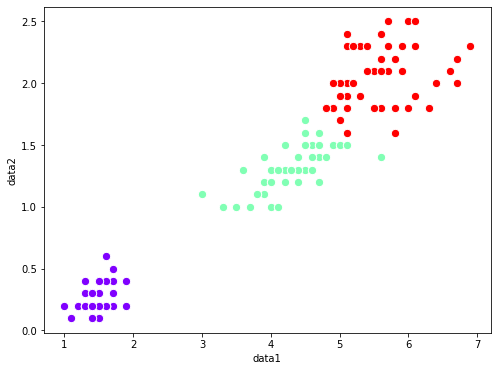
分類できていますね。
量子Neural Network
量子分類器をやってみます。
古典NNと量子NNのハイブリッドになっています。
import tensorflow as tf
import keras_metrics
n_qubits = 2
layers = 4
data_dimension = 3 # output
param = {'num_epochs': 128}
dev = qml.device("default.qubit", wires=n_qubits)
@qml.qnode(dev, diff_method='adjoint')
def qnode(inputs, weights):
qml.templates.AngleEmbedding(inputs, wires=range(n_qubits))
qml.templates.StronglyEntanglingLayers(weights, wires=range(n_qubits))
return [qml.expval(qml.PauliZ(i)) for i in range(n_qubits)]
weight_shapes = {"weights": (layers, n_qubits,3)}
qlayer = qml.qnn.KerasLayer(qnode, weight_shapes, output_dim=n_qubits)
clayer1 = tf.keras.layers.Dense(n_qubits, activation='relu')
clayer2 = tf.keras.layers.Dense(3, activation="softmax")
model = tf.keras.models.Sequential([clayer1,qlayer,clayer2])
opt = tf.keras.optimizers.Adam(learning_rate=0.05)
model.compile(opt, loss='categorical_crossentropy')
hist = model.fit(x_train, y_train, validation_split=0.1, epochs=param['num_epochs'], verbose=1, shuffle='True', batch_size=30, callbacks=[early_stopping])
loss = hist.history['loss']
val_loss = hist.history['val_loss']
# lossのグラフ
plt.plot(range(len(loss)), 10*np.log10(loss), marker='.', label='loss')
plt.plot(range(len(val_loss)), 10*np.log10(val_loss), marker='.', label='val_loss')
plt.legend(loc='best', fontsize=10)
plt.grid()
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()
Epoch 1/128 5/5 [==============================] - 3s 603ms/step - loss: 1.1991 - val_loss: 0.9448 Epoch 2/128 5/5 [==============================] - 3s 581ms/step - loss: 0.8379 - val_loss: 0.8937 Epoch 3/128 5/5 [==============================] - 3s 605ms/step - loss: 0.6726 - val_loss: 1.0398
1 epochは50データしか無いのですが、それに3秒もかかっています。。
古典NNの数十倍も遅いです。
結果を可視化してみます。
はい、量子でも分類できていますね。
色々遊んでみるとよいかと思います。
例えば、初段の古典NNのactivationを線形(linear)にしても、量子層の非線形性がちゃんと分類をやってくれます。
勾配計算手法と計算時間
量子機械学習の場合、勾配計算のやり方によって計算時間は随分違います。
上の例では diff_method = "adjoint" というものを使っています。
もう少し愚直な "parameter-shift" を使ってみると、
Epoch 1/128 5/5 [==============================] - 12s 2s/step - loss: 1.1966 - val_loss: 1.5186
このように、adjointの3倍程度遅くなります。
かつ、この方法はパラメータ数に比例した計算時間がかかっていきます。1
他に、backpropagationを使うことも出来ます。仕組みは古典NNのものと同じです。
引数として backprop を指定すればいい・・・のですが、加えてインターフェースとしてtensorflow(tf)を明示する必要があります。
dev = qml.device("default.qubit.tf", wires=n_qubits)
@qml.qnode(dev, diff_method='backprop', interface="tf")
Epoch 1/128 5/5 [==============================] - 9s 2s/step - loss: 0.8118 - val_loss: 0.9497
parameter-shiftより若干早い程度です。
backpropの原理的には、もっと速いと思うのですが、、謎です。
というわけで、今の実装ですとadjointが良さそうです。
それでも、古典NNより遥かに計算が遅いです。
まとめ
量子機械学習は計算時間にご注意を。
-
paramet-shiftの利点として、実機でも使えます。backprop,adjoint等はシミュレーター専用アルゴリズムです。これらのアルゴリズムでは、量子回路の途中の状態ベクトルを観測する必要があります。実機でそれをやると、観測した段階で状態が破壊されてしまいます。 ↩