量子機械学習（量子NN)における勾配計算

量子機械学習のうち、量子回路をブラックボックスモデルとして学習させるものがあります。
（量子回路学習とかいいます）

古典NNの場合、勾配降下法で効率よくパラメータを探索できます。
そして勾配計算自体も、逆伝播法と呼ばれる効率的な計算方法があります。
これの量子版を考えます。

勾配計算の問題

量子機械学習でも、勾配降下法は利用できます。
が、どうやって勾配を計算するかが最初の問題です。

最も簡単で汎用的なアイデアは、数値差分です。
つまり、パラメータを少しシフトしたforward propagationを行って、シフト前の結果と差分を取ることで
勾配を計算します。
実際、量子でも数値差分によく似た（しかしそれよりも賢い）方法として　parameter-shift rule と呼ばれる方法があります。
しかし、勾配計算はパラメータそれぞれに対して必要ですので、 2×パラメータ数×forward propagation の計算時間　を要します。
量子計算では、シミュレーターの場合、forward propagation　1回の計算時間はかなり大きくなりやすいです。
これは、量子ビット数が$N$の場合に、その状態計算は$2^{N} \times 2^{N}$の行列を繰り返し掛けることで表現しなければならないためです。
実機では、物理的な量子系が計算をしてくれますので、forward propagation　1回の計算時間は問題になりにくいと思いますが。

次に考えるアイデアは、なんとか古典NNの逆伝播を真似できないかということです。
量子回路でも、少なくともシミュレーションではback propagationが出来ることが知られています。
back propagationができれば、forward propagation　は1度で済むので、大きな計算量削減になります。
今回はこれを示します。

ただし、実機では難しい部分があります。
back propagationでは、量子回路の各層における状態を知る必要があります。
状態を知る　とは、量子系においては測定をすることと同じです。
量子系では、測定をすると状態が（一般には）変化しますので、以後の回路が無意味になってしまいます。
なので、実機ではシミュレーションのような方法ではback propagationが出来ません。
このあたりは色々検討中のようです。例えば下記。

株式会社グリッド：「量子コンピュータ上で動作する逆伝播勾配降下法（Backpropagation）」の開発成功に関するお知らせ

PennyLaneでのback propagation

PennyLane (python SDK)では、back propagationが実装されています。助かる。
本当に早いんでしょうか？　parameter-shift と比較してみました。

code

%matplotlib inline
import pennylane as qml
from pennylane.templates import RandomLayers
from pennylane.templates.embeddings import AngleEmbedding
from pennylane import numpy as np
import matplotlib.pyplot as plt
import time

########  パラメータ  #############
n_qubits = 8 ## qubitの数
n_layers = 1 # q_layer
N_dim = 1 # 入力データベクトルの次元。 N_dim < n_qubits　でなければならない
N_data = 64 # トレーニングデータ数

# Random circuit parameters
rand_params = np.random.uniform(high=2 * np.pi, size=(n_layers, n_qubits))

dev = qml.device("default.qubit", wires=n_qubits,analytic=True) # define a device

def layer(v):
    for i in range(n_qubits):
        # variational gates
        qml.RX(v[3*i],wires=i)
        qml.RZ(v[3*i+1],wires=i)
        qml.RX(v[3*i+2],wires=i)
        # randomizer
        RandomLayers(rand_params, wires=list(range(n_qubits)))        

@qml.qnode(dev, diff_method="parameter-shift")

def quantum_neural_net(var, x):
    angle_y = 2*np.arccos(x)
    for i in range(n_qubits):
        loc = i%N_dim
        # data embedding as angles
        qml.RY(angle_y[loc], wires=i)
    # "layer" subcircuits
    for v in var:
        layer(v)

    return qml.expval(qml.PauliZ(0))


def square_loss(desired, predictions):
    loss = 0
    for l, p in zip(desired, predictions):
        loss = loss + (l - p) ** 2
    loss = loss / len(desired)
    return loss

def cost(var, features, desired):
    preds = [quantum_neural_net(var, x) for x in features]
    return square_loss(desired, preds)

#パラメータ初期化
np.random.seed(0)
var_init = 0.05 * np.random.randn(n_layers, 3*n_qubits)
print(var_init)

# 入力トレーニング用データ
X = 1-2*np.random.rand(N_data,N_dim) # -1 ~ +1
# 目標データ
Y = X[:,0]



#from pennylane.optimize import AdamOptimizer
#opt = AdamOptimizer(0.01, beta1=0.9, beta2=0.999)
opt = qml.GradientDescentOptimizer(0.1)
#opt = qml.RMSPropOptimizer()

hist_cost = []
var = var_init

# 処理前の時刻
t1 = time.time() 
for it in range(1):
    var, _cost = opt.step_and_cost(lambda v: cost(v, X, Y), var)
    print("Iter:"+str(it)+" | cost:"+str(_cost.numpy()))
    hist_cost.append(_cost)

# 処理後の時刻
t2 = time.time() 
# 経過時間を表示
elapsed_time = t2-t1
print(f"経過時間：{elapsed_time}")

t1_cost = time.time()
cost(var,X,Y)
t2_cost = time.time()
elapsed_time_cost = t2_cost-t1_cost
print(f"cost計算のみの時間:{elapsed_time_cost}")

diff-method のところで"backprop"と"parameter-shift"が変えられます。

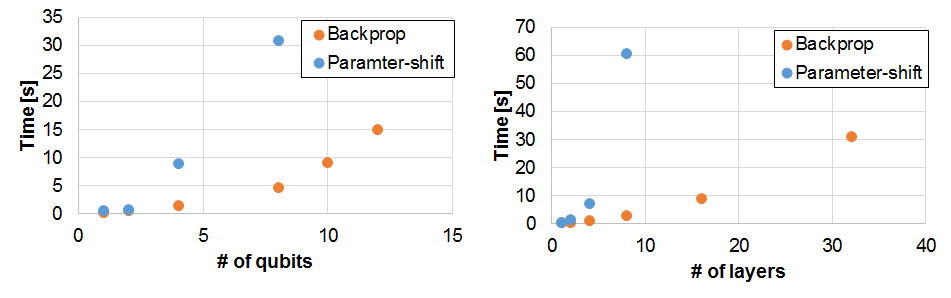
総計算時間

forward propagation ＋勾配計算　からなる総計算時間を
量子ビット数および層数を変えてみてみます。

Back propagationのほうが確かに圧倒的に早いです。

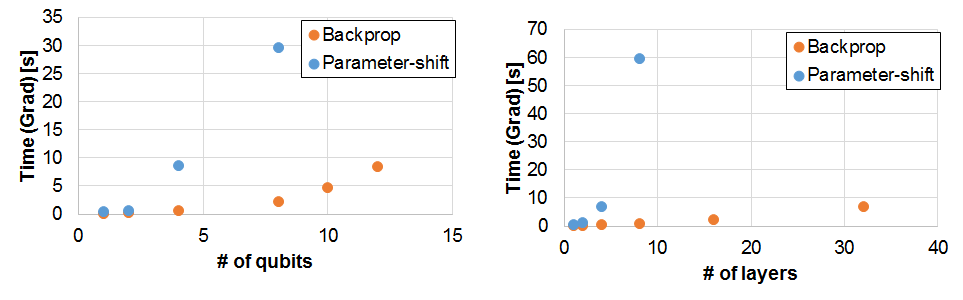
勾配計算時間

勾配計算だけの時間をみてみます。
簡単のために、総計算時間からforward propagation 1回の時間を引いたもので定義しました。

再び、Back propagationのほうが確かに圧倒的に早いです。
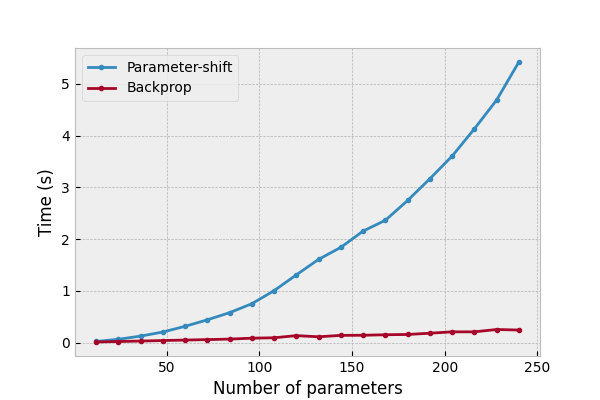
注目すべきは、層数を増やす（＝パラメータ数を増やす）ことをしても、勾配計算の時間がほぼ変わっていません。
back propagationでは、パラメータ数が増えてもforward propagationは1回しか必要ありませんので、計算時間が節約されます。
PennyLaneの公式にも同様の記載があります。

まとめ

PennyLaneのback propagationは助かる。

PennyLaneによる量子機械学習 ~勾配計算の匠~